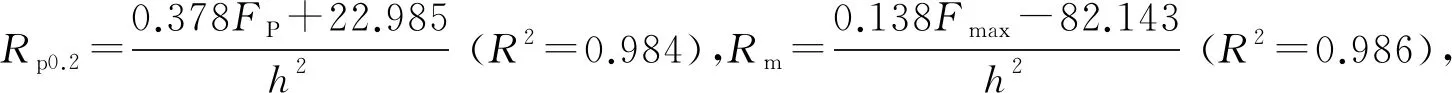小沖桿試驗評估X80管線鋼的拉伸性能

宋 明，李旭陽，曹宇光，司偉山，甄 瑩

(中國石油大學(xué)(華東)儲運與建筑工程學(xué)院，青島 266580)

0 引 言

小沖桿試驗(Small Punch Test，SPT)是一種通過測試從在役設(shè)備上取得的微小圓片狀試樣，進(jìn)而對設(shè)備材料劣化性能和剩余壽命進(jìn)行近乎“無損評價”的新型試驗方法[1-3]。與常規(guī)單軸拉伸試驗相比，其所需試樣尺寸極小：直徑d1為10.0 mm，厚度h為0.300～0.500 mm[4]。試驗時將薄片試樣邊緣固定，用頭部半徑r=1.25 mm的沖桿對試樣中心進(jìn)行擠壓加載直至破壞，得到小沖桿試驗載荷-位移曲線，然后與常規(guī)單軸拉伸試驗結(jié)果進(jìn)行關(guān)聯(lián)即可確定材料的彈性與塑性等力學(xué)性能。通常來說，小沖桿試驗結(jié)果受試樣厚度的影響較大[5-7]。目前，國內(nèi)外學(xué)者通過對多種材料進(jìn)行試驗，得到了小沖桿試驗與常規(guī)拉伸試驗進(jìn)行關(guān)聯(lián)所需的經(jīng)驗公式[8-10]，但忽略了試樣厚度變化的影響。作者在借助韓浩等[8]與MAO等[10]給出的經(jīng)驗公式(作者未考察其他經(jīng)驗公式對X80管線鋼小沖桿試驗的適用性)對X80管線鋼小沖桿試驗結(jié)果進(jìn)行處理時發(fā)現(xiàn)，試樣的屈服強度與抗拉強度對厚度有極大的依賴性，所得結(jié)果與單軸拉伸的相比誤差較大。雖然有學(xué)者對此經(jīng)驗公式進(jìn)行了一定改進(jìn)[11]，但其并不適用于X80管線鋼。

數(shù)字圖像相關(guān)(Digital Image Correlation，DIC)是一種新型應(yīng)變測量技術(shù)，其原理是通過跟蹤試樣表面變形前后兩幅散斑圖像中同一像素點的位置來獲得該像素點的位移向量，從而計算試樣表面的全場應(yīng)變。DIC技術(shù)可以在試樣表面設(shè)置虛擬引伸計。虛擬引伸計在力學(xué)測試中比常規(guī)接觸式引伸計有著更廣的適用范圍，對于應(yīng)變的分辨率較高，并且可以測得單軸拉伸試樣頸縮處的應(yīng)變值。作者借用DIC技術(shù)，對X80管線鋼進(jìn)行單軸拉伸與小沖桿試驗，系統(tǒng)地研究了試樣厚度對小沖桿試驗所得彈性模量、屈服載荷、最大載荷的影響，并給出了以厚度為自變量的新型屈服強度、抗拉強度經(jīng)驗公式。

1 試樣制備與試驗方法

試驗材料為X80管線鋼，其化學(xué)成分如表1所示。

表1 X80管線鋼的化學(xué)成分(質(zhì)量分?jǐn)?shù))

按照GB/T 228.1-2010加工光滑圓棒狀拉伸試樣，標(biāo)距段尺寸為φ10 mm×50 mm，采用CTM9100型微機控制電子萬能試驗機進(jìn)行單軸拉伸試驗，應(yīng)變速率為5×10-4s-1，測3個平行試樣。按照GB/T 29459.1-2012，從X80管線鋼上截取直徑為10.0 mm、厚度為0.600 mm的小沖桿試樣，用砂紙進(jìn)行打磨去除過熱影響區(qū)和加工硬化影響區(qū)。試樣最終厚度分別為0.300，0.350，0.400，0.450，0.500，0.550 mm，厚度測試精度為±0.005 mm。采用自行設(shè)計研發(fā)的SPT-10型試驗機進(jìn)行小沖桿試驗，試驗裝置如圖1所示，整個加載過程通過計算機控制，沖頭速度為0.2～0.5 mm·min-1，各測3個平行試樣。

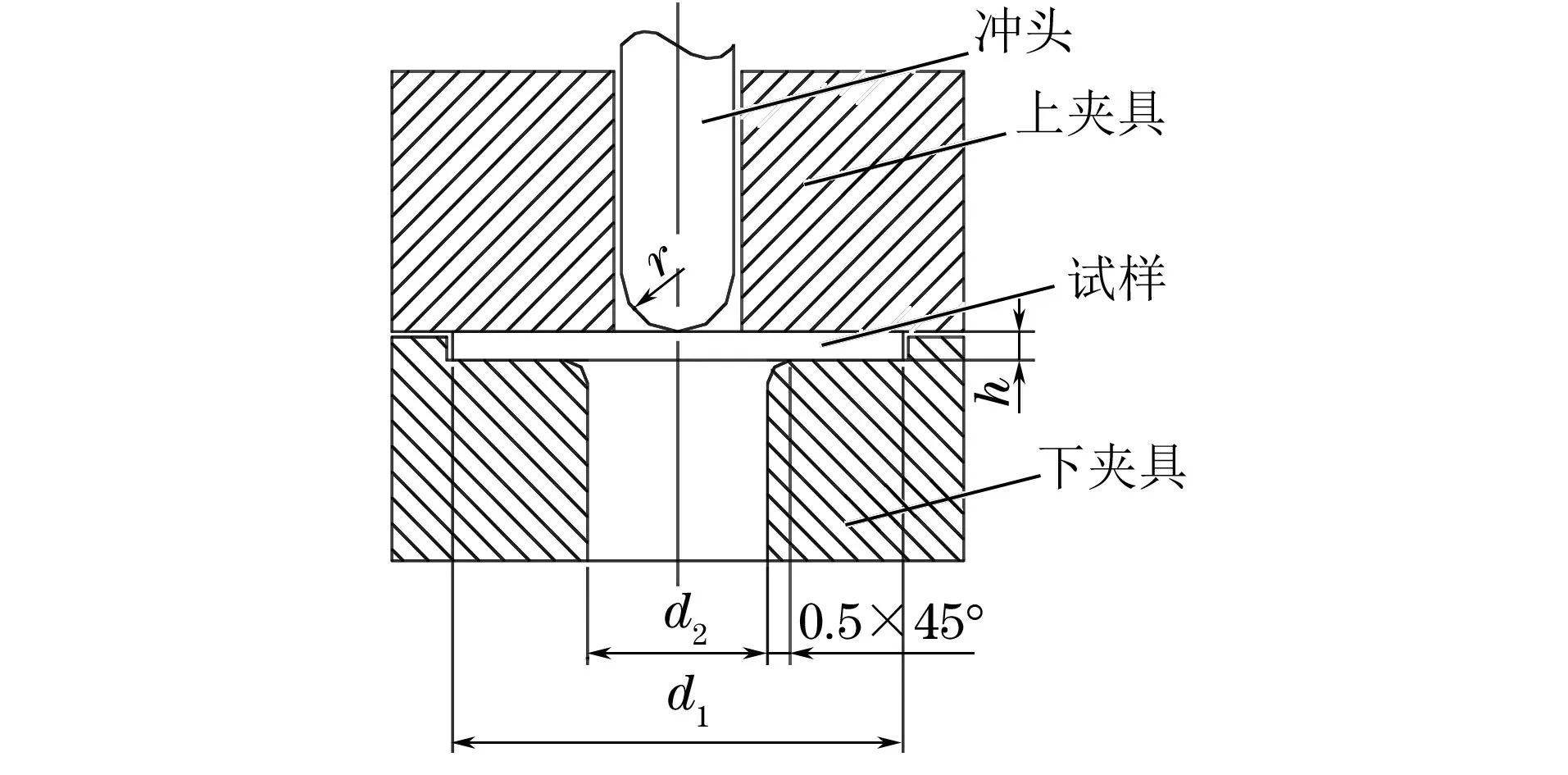
圖1 小沖桿試驗裝置示意

單軸拉伸試驗開始前，在試樣表面均勻噴制黑色白底散斑點作為DIC測量參考點，通過標(biāo)定板建立試樣表面散斑點的三維坐標(biāo)。試驗開始后，由萬能試驗機對試樣進(jìn)行加載，同時DIC測量系統(tǒng)以每秒10張圖像的速度記錄試驗應(yīng)變。

2 試驗結(jié)果與討論

2.1 單軸拉伸性能

將DIC計算得到的應(yīng)變與萬能試驗機得到的應(yīng)力相結(jié)合，得到X80管線鋼的工程應(yīng)力-應(yīng)變曲線，如圖2所示。可知其彈性模量E為206.04 GPa，屈服強度RP0.2為594 MPa，抗拉強度Rm為713 MPa。

圖2 X80管線鋼單軸拉伸試驗結(jié)果

2.2 小沖桿試驗評估力學(xué)性能

2.2.1 典型載荷-位移曲線

由圖3可知，X80管線鋼小沖桿試驗的載荷-位移曲線分為4個階段：彈性彎曲階段(Ⅰ)、塑性彎曲階段(Ⅱ)、薄膜伸張階段(III)、塑性失穩(wěn)階段(Ⅳ)。彈性彎曲階段的斜率主要受到材料彈性模量的影響。

圖3 小沖桿試驗典型載荷-位移曲線

2.2.2 彈性模量的確定

小沖桿試驗過程中彈性階段極短，且該階段試樣變形極小，符合小變形假設(shè)，即試樣變形前后尺寸不變[12]。將小沖桿試樣近似視作周邊固定的半徑為R(R為下夾頭孔徑d2的1/2)的薄圓板，彈性試驗階段，試樣在中心半徑為R1(R1為沖頭與試樣接觸部分的半徑)的圓內(nèi)受大小為q的均布載荷作用。根據(jù)彈性薄板理論，此時圓板中心點的位移，即試樣中心撓度u[13]為

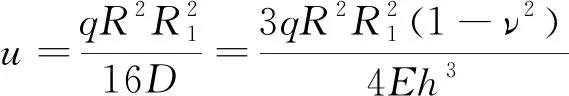
(1)

式中：D為試樣的彎曲剛度；E和ν分別為試樣的彈性模量和泊松比。

試樣受到的載荷F為

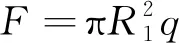
(2)

將式(2)代入式(1)得到材料的彈性模量E為

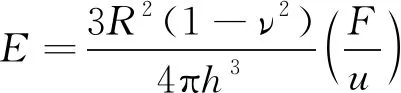
(3)

F/u即為小沖桿試驗載荷-位移曲線第一階段的斜率。

在試驗過程中，沖頭與試樣接觸面積不斷增大，且接觸位置迅速進(jìn)入塑性階段，基于彈性假設(shè)得到的位移量必然小于真實位移量，因此通過式(3)計算得到的彈性模量與實際的相比偏小。羅紅花等[12]通過4種材料的小型沖壓試驗和有限元分析對式(3)進(jìn)行修正，引入了修正系數(shù)λ(λ=1.328 4)，修正后的公式為

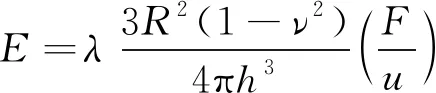
(4)

從表2可以看出：隨著試樣厚度的增加，小沖桿試驗載荷-位移曲線第一階段的斜率增大；利用式(4)計算得到的彈性模量與單軸拉伸試驗測試值的相對誤差均小于9.2%，說明修正后的彈性模量經(jīng)驗公式適用于X80管線鋼，且基本不受試樣厚度變化的影響。

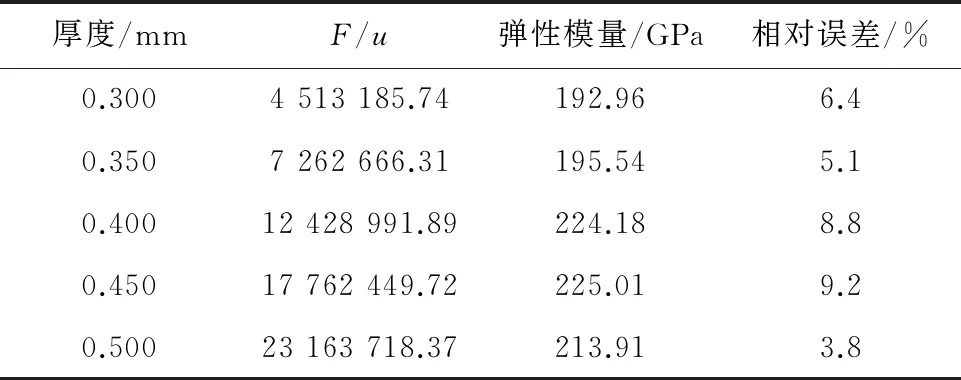
表2 采用式(4)計算得到的不同厚度X80管線鋼的彈性模量

2.2.3 屈服強度的確定

屈服載荷為材料從彈性階段向塑性階段過渡時對應(yīng)的載荷，但小沖桿試驗載荷-位移曲線上無明顯屈服平臺，彈性向塑性的過渡緩慢，表現(xiàn)為一段圓滑的曲線，屈服載荷不易確定。為此，利用最小二乘法[8]對載荷-位移曲線上彈性彎曲階段、塑性彎曲階段，即屈服載荷附近的曲線重新進(jìn)行擬合，兩擬合曲線的交點(A)對應(yīng)的載荷即為屈服載荷FP，如圖4所示。

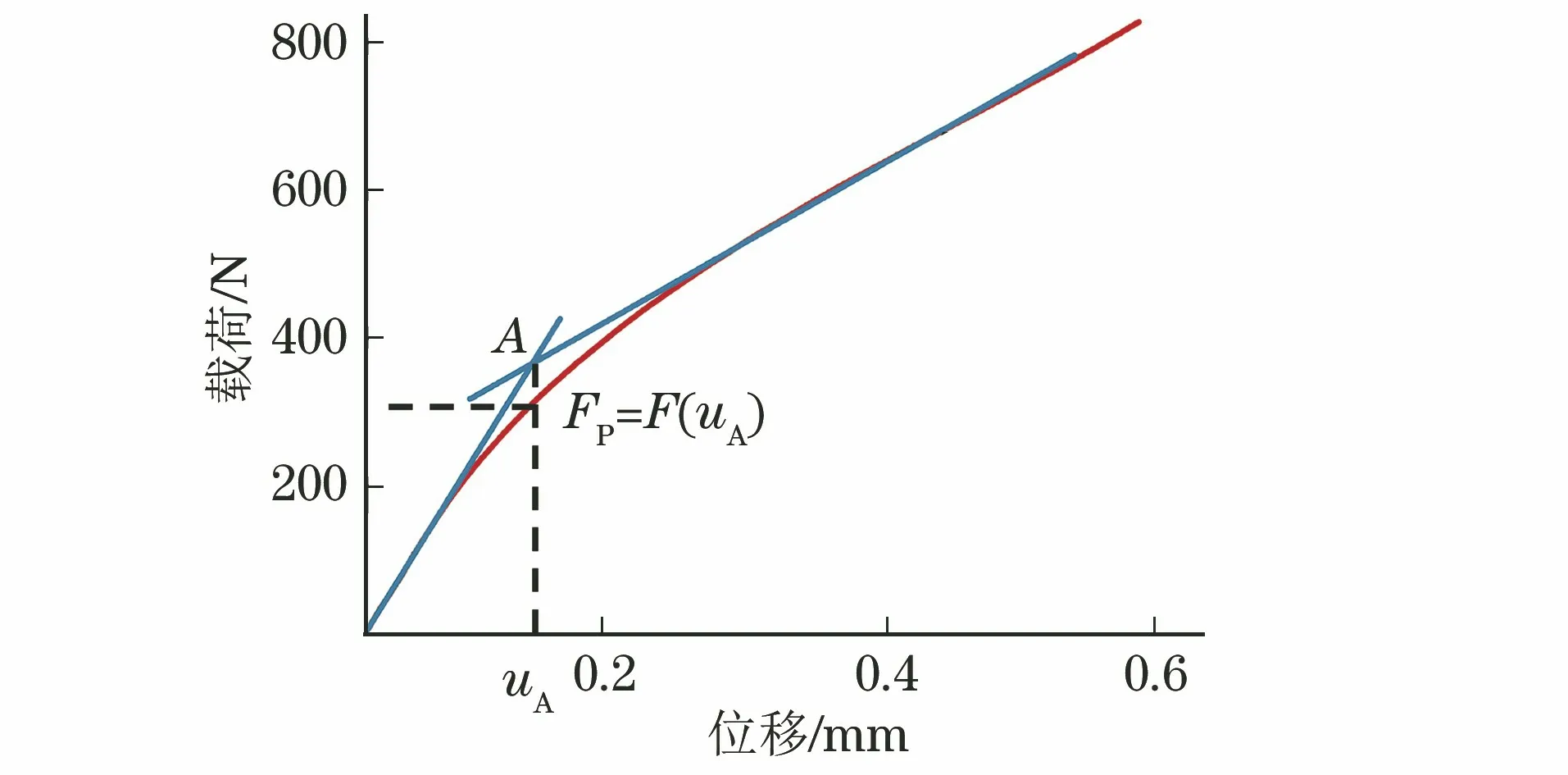
圖4 屈服載荷確定方法示意

由表3可以看出，隨試樣厚度增大，X80管線鋼屈服載荷不斷增大。這是由于試樣的承壓能力隨厚度增加逐漸增大，發(fā)生屈服時的載荷亦隨之增大。

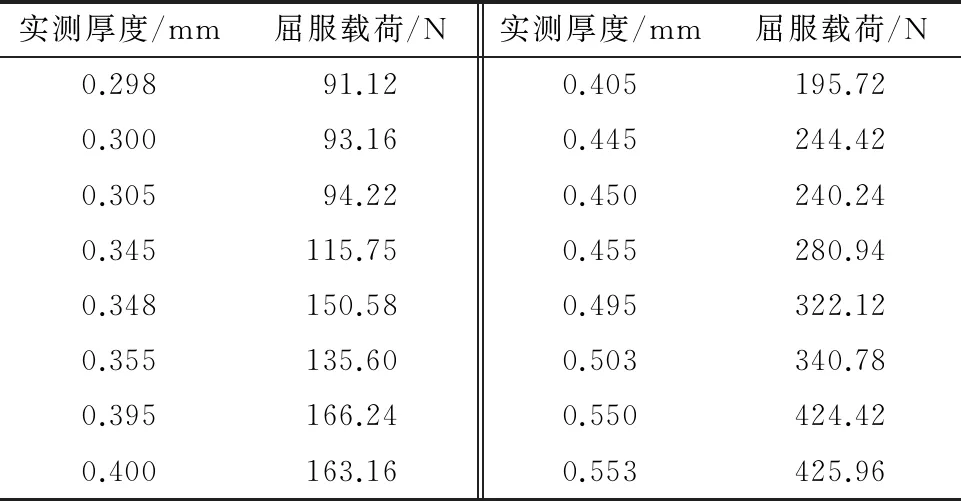
表3 不同厚度X80管線鋼小沖桿試樣的屈服載荷

在數(shù)據(jù)處理過程中發(fā)現(xiàn)，屈服載荷與厚度之間存在二次函數(shù)關(guān)系，為了簡化公式并滿足量綱要求，將屈服載荷FP與試樣厚度的平方h2相關(guān)聯(lián)，兩者之間成線性關(guān)系，如圖5所示。相關(guān)系數(shù)為0.992，決定系數(shù)為0.984。

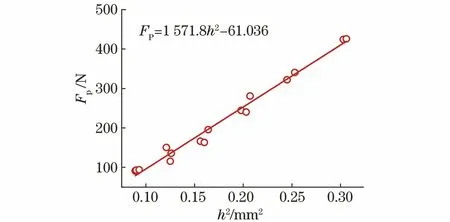
圖5 FP與h2的關(guān)系曲線

基于上述分析結(jié)果,建立一種新的經(jīng)驗公式,即

FP=A1Rp0.2h2+B1

(5)

式中：A1，B1為待定系數(shù)。

令Rp0.2=594 MPa(單軸拉伸試驗結(jié)果)，則聯(lián)立式(5)和圖5中FP與h2擬合公式，可得A1=2.646，B1=-61.036。將A1和B1代入式(5)，得到X80管線鋼小沖桿試驗屈服強度的經(jīng)驗公式為

Rp0.2=(0.378FP+22.985)/h2

(6)

韓浩等[8]及MAO等[10]給出的小沖桿試驗屈服強度經(jīng)驗公式分別為

Rp0.2，Han=0.5FP/h2

(7)

Rp0.2，Mao=0.36FP/h2

(8)

將試驗所得不同厚度試樣的屈服載荷分別代入式(6)～(8)，結(jié)果如圖6所示。可見利用式(7)和式(8)計算得到的X80管線鋼的屈服強度均隨著試樣厚度的增加而增大，尤其是式(8)所得結(jié)果，相比于單軸拉伸屈服強度的誤差極大。而利用式(6)所得屈服強度的準(zhǔn)確性較高，與單軸拉伸試驗結(jié)果的相對誤差均小于11.2%，并且隨著試樣厚度的增大，誤差越來越小。厚度較小的試樣在進(jìn)行小沖桿試驗時會迅速屈服進(jìn)入塑性彎曲階段，在確定第一階段范圍時，將不可避免地包含過多彈性-塑性過渡區(qū)域，因此厚度較小試樣的屈服強度計算誤差普遍偏大。

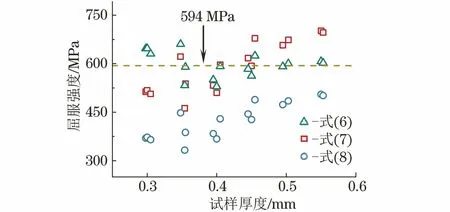
圖6 不同小沖桿試驗經(jīng)驗公式計算得到X80管線鋼的屈服強度

2.2.4 抗拉強度的確定

通過小沖桿試驗獲得材料的抗拉強度相對簡單，只需將小沖桿試驗載荷-位移曲線中最大載荷Fmax與單軸拉伸抗拉強度Rm相關(guān)聯(lián),即可建立經(jīng)驗關(guān)系式。不同厚度X80管線鋼小沖桿試樣的最大載荷如表4所示。

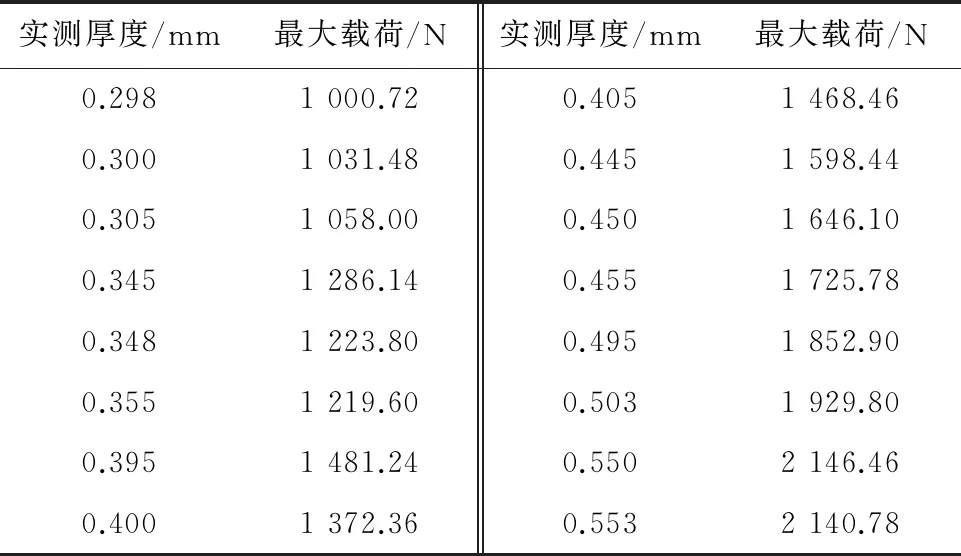
表4 不同厚度X80管線鋼小沖桿試樣的最大載荷

與屈服載荷類似，最大載荷Fmax與試樣厚度的平方h2亦具有線性關(guān)系，如圖7所示，相關(guān)系數(shù)為0.994，決定系數(shù)為0.986。

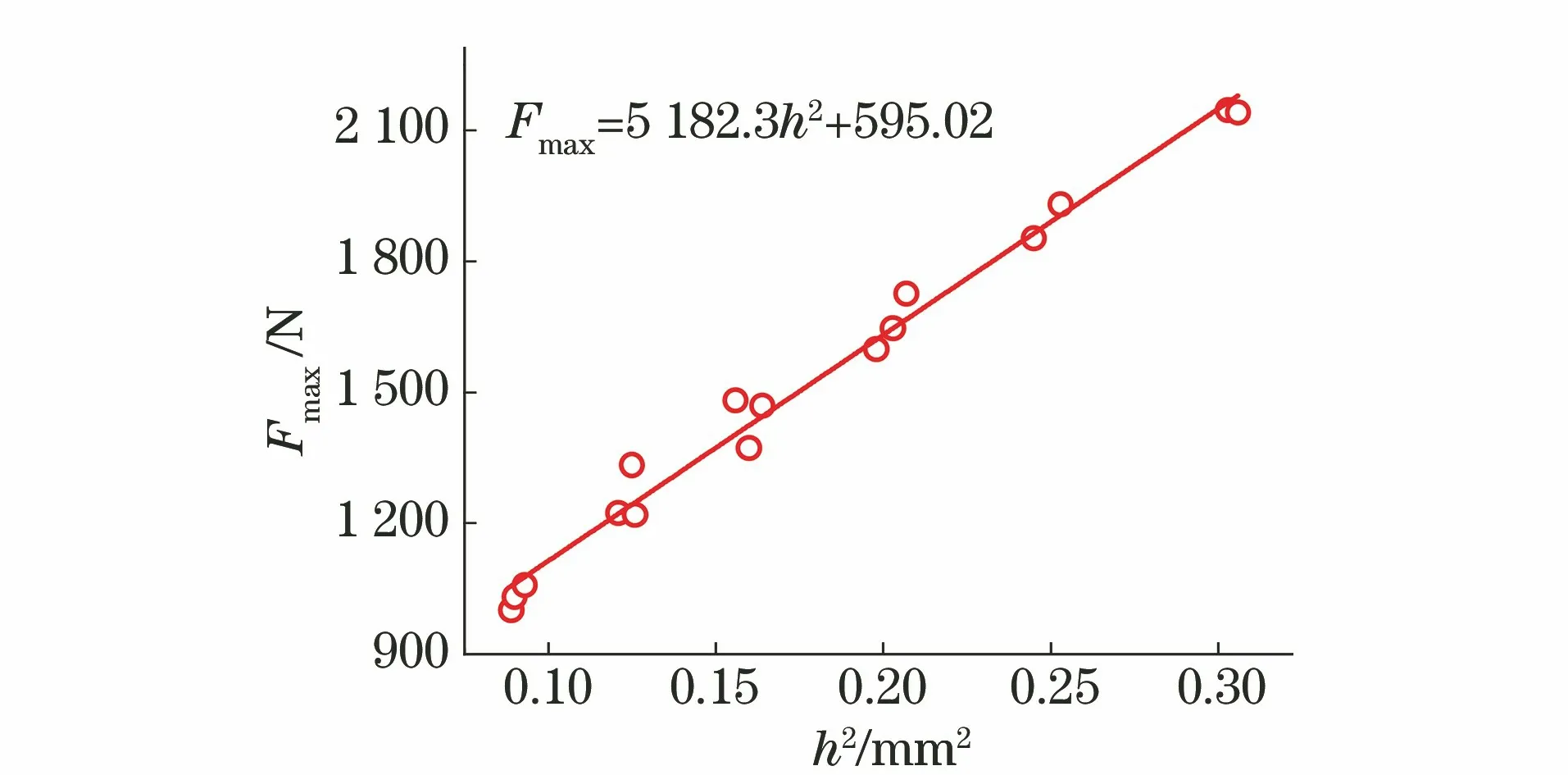
圖7 Fmax與h2的關(guān)系曲線

最大載荷與試樣厚度的關(guān)系式為

Fmax=A2Rmh2+B2

(9)

式中：A2，B2為待定系數(shù)。

令Rm=713 MPa(即單軸拉伸抗拉強度)，則聯(lián)立式(9)和圖7中Fmax與h2擬合公式，可得A2=7.27，B2=595.02。將A2和B2代入式(9),得到X80管線鋼小沖桿試驗抗拉強度經(jīng)驗公式為

Rm=(0.138Fmax-82.143)/h2

(10)

韓浩等[8]及MAO等[10]給出的小沖桿試驗抗拉強度經(jīng)驗公式分別為

Rm，Han=0.11Fmax/h2-77

(11)

Rm，Mao=0.13Fmax/h2-0.32

(12)

將試驗所得不同厚度試樣的最大載荷分別代入式(10)～(12)，計算結(jié)果如圖8所示。可以看出，通過式(11)和式(12)計算得到的抗拉強度隨著試樣厚度的增加而減小，當(dāng)試樣厚度小于0.500 mm時，計算結(jié)果遠(yuǎn)高于單軸拉伸試驗結(jié)果，說明這兩種經(jīng)驗公式已不適用于X80管線鋼。利用式(10)所得抗拉強度受厚度變化影響不大，與單軸拉伸試驗結(jié)果的相對誤差均小于12.3%。在試樣厚度較小時，誤差相對較大。這是由于小沖桿試樣尺寸極小，存在各向異性與尺度效應(yīng)[14]，并且在發(fā)生塑性變形時，試樣中的孔洞、夾雜物等缺陷還極易引發(fā)裂紋的萌生與擴(kuò)展[15]，造成最大載荷不穩(wěn)定，進(jìn)而導(dǎo)致抗拉強度計算誤差偏大。

圖8 不同小沖桿試驗經(jīng)驗公式計算得到X80管線鋼的抗拉強度

3 結(jié) 論

(1) X80管線鋼單軸拉伸試驗測得的彈性模量為206.04 GPa，屈服強度為594 MPa，抗拉強度為713 MPa。