基于灰狼算法的模塊化關節摩擦辨識和補償

崔靖凱，賽華陽，張恩陽，朱明超 ，徐振邦，3*

（1. 中國科學院長春光學精密機械與物理研究所，吉林長春130033；2. 中國科學院大學，北京 100049；3. 中國科學院大學材料與光電研究中心，北京100049）

1 引 言

模塊化關節能通過重構組合，使機械臂形成不同功能的構型，滿足不同環境和任務的需求。具有模塊化關節的機械臂制造成本低、設計周期短、互換性強并易于改進，被廣泛應用于各個領域［1］。為了獲得高負載自重比，模塊化關節常具有諧波減速器等非線性環節，這增大了摩擦干擾，影響機械臂的定位和跟蹤精度。

摩擦補償是減少或消除關節非線性環節的不利影響、提高系統動態性能的重要途經。摩擦補償包括基于摩擦模型的補償和不基于摩擦模型的補償。其中，基于摩擦模型的補償由于具有可預見、響應速度快等特點［2］，獲得了廣泛應用。模塊化關節的摩擦模型包括庫倫-黏性摩擦模型［3］、Stribeck 摩擦模型［4］、LuGre 摩擦模型［5］等。庫侖-黏性摩擦模型和Stribeck 摩擦模型無法描繪電機速度接近于零時的預滑動區域的摩擦特性，導致電機速度換向時補償的摩擦力不連續，引起力矩的跳變。為了充分考慮摩擦的非線性特性，保證補償力矩的連續性，本文基于LuGre摩擦模型進行摩擦補償。

摩擦模型參數的準確度直接影響了摩擦模型的精度，進而影響摩擦補償的效果［6］，因此需要對模型參數進行辨識。參數辨識是指在滿足激勵的條件下，采集系統的狀態信息對物理參數進行估計的過程［7］。參數辨識可以分為在線辨識和離線辨識。在線辨識適用于對環境變化敏感的參數，如溫度的變化、材料的磨損等，雖然具有高精度和實時響應的優點，但可能存在參數收斂不完全的問題，且受到實驗對象能否實時執行的限制。離線辨識相對簡單易行，在對環境變化不敏感的參數如力矩系數、摩擦系數等上更具優勢，因此，本文采用離線辨識的方法。

針對LuGre 模型，學者們提出了多種辨識方法。肖前進［8］等用分段最小二乘法辨識了LuGre模型的靜態參數，將電機預滑動區域的特征作線性化處理，等價為一個二階系統，計算得到動態參數。該方法需要對實驗數據分段辨識，預滑動區域的線性化處理會引入建模誤差、計算誤差等，影響辨識精度。為了提高辨識精度，元啟發式算法成為研究熱點。于偉［9］等用一般辨識方法辨識了靜態參數，并以轉速變化為目標函數，用遺傳算法擬合出動態參數；曾德林［10］等用分步夾逼和分步搜索法初步辨識了摩擦參數，然后用遺傳算法提高辨識精度。

灰狼算法是由SEYEDALI M［11］提出的元啟發式優化算法，模仿自然界中灰狼的領導階層和捕獵機制。灰狼算法具有簡單易用、靈活性強和避免局部最優等優點，適用于多參數辨識的情況。相較于工程常用的最小二乘法，無需對數據分段處理，在辨識非線性模型方面具有優勢。

本文針對自主研發的模塊化關節，選用能較為全面地描述摩擦特性的LuGre 模型，分別用基于分段最小二乘法的一般辨識方法和基于灰狼算法的元啟發式辨識方法對摩擦參數進行辨識，并將辨識結果對比分析，最后通過前饋補償算法對摩擦力進行補償。實驗結果表明，相比于一般辨識方法，灰狼算法在摩擦辨識領域精度更高、適用性更強；本文提出的摩擦補償方法能顯著減小關節速度跟蹤誤差，提高控制品質。

2 模塊化關節系統及建模

2.1 關節結構

圖1 為模塊化關節的內部構造示意圖。關節主要由外殼、無框力矩電機、諧波減速器、電磁制動器、增量式編碼器、絕對式編碼器和驅動電路板構成。左側和下側的電連接板用于給相鄰關節供電通訊，方便關節的裝卸和組合，體現模塊化的特點。關節采用雙編碼器設計，增量式編碼器獲取的相對位置信息通過差分運算得到速度信息，絕對式編碼器用于獲取關節負載端的絕對位置信息。

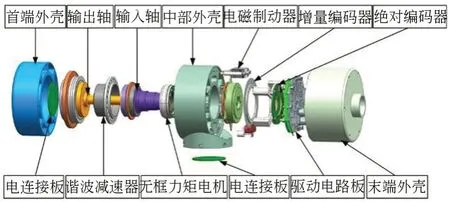
圖1 模塊化關節結構圖Fig.1 Structure of modular joint

2.2 控制系統

關節采用位置-速度-電流三閉環控制，控制框圖如圖2 所示。計算機使用倍福公司的Twin?CAT 軟件對關節發送指令，關節的驅動電路板接收到位置或速度指令，通過控制q軸電流驅動電機轉子和輸入軸轉動，諧波減速器的波發生器與輸入軸固連，經減速后的輸出軸與負載連接，實現力矩的輸出。

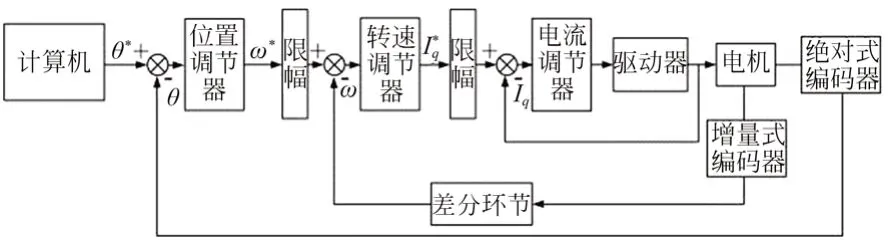
圖2 模塊化關節控制框圖Fig.2 Block diagram of modular joint control system

2.3 動力學模型

建立模塊化關節的簡化動力學模型如圖3 所示，其動力學方程為：

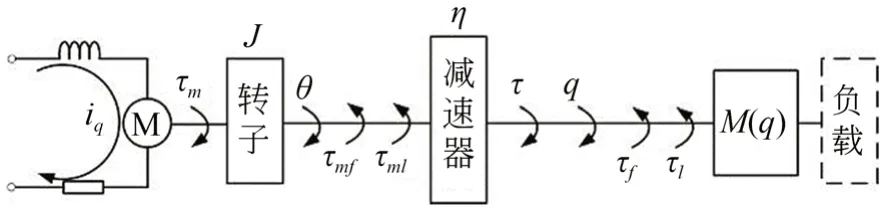
圖3 模塊化關節動力學模型Fig.3 Dynamic model of modular joint

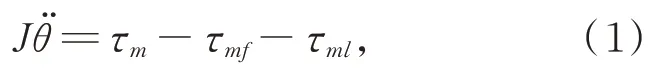
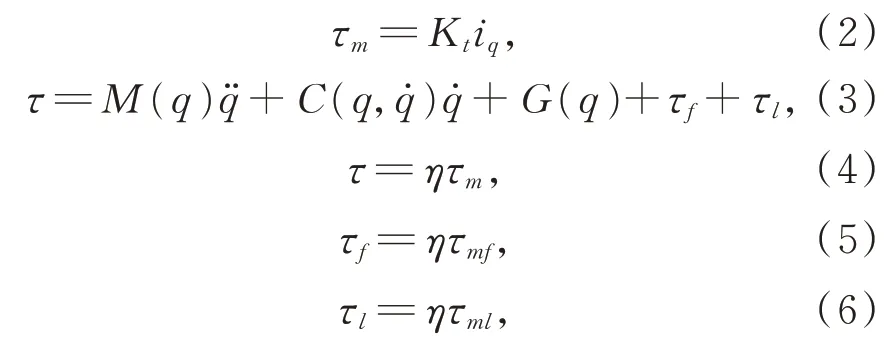
其中：J為電機轉子及波發生器折算到電機端的轉動慣量；θ為電機轉角；τm為電機端輸出力矩，τmf和τml分別為折算到電機端的摩擦力矩和負載力矩；Kt為力矩系數；iq為q軸電流；τ為關節端輸出力矩分別為關節端角度、角速度、角加速度；M(q)q?為連桿慣性項為離心力和科氏力項；G(q)為重力項；τf和τl分別為關節端摩擦力矩和負載力矩；η為諧波減速器的減速比。為了統一度量，本文均采用關節端的物理量作為實驗和計算數據。

3 摩擦參數辨識

3.1 LuGre 摩擦模型

摩擦來源于接觸器件的相對運動。對于模塊化關節，諧波減速器的波發生器和柔輪的相對運動、柔輪和鋼輪的相對運動都會產生摩擦。此外，電機輸入軸、輸出軸的支撐軸承也存在摩擦。

LuGre 摩擦模型為：

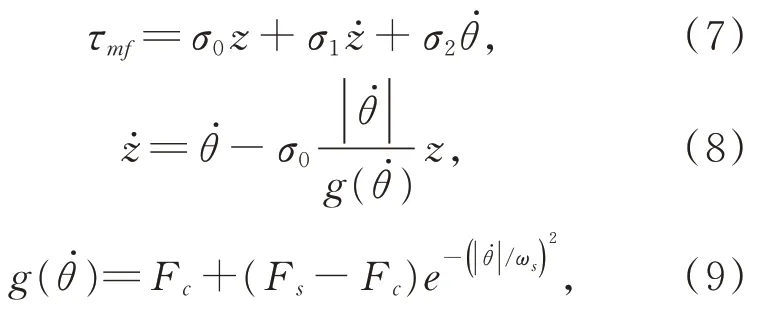
其中：z為鬃毛平均形變量，σ0為鬃毛剛度，σ1為鬃 毛 阻 尼 系 數 ，σ2為 黏 滯 摩 擦 系 數為Stribeck 效應，Fc為庫侖摩擦力，Fs為最大靜摩擦力，ωs為Stribeck 速度。模型包括四個靜態參數Fc、Fs、ωs和σ2，以及兩個動態參數σ0和σ1。

3.2 基于分段最小二乘法的一般辨識方法

一般辨識方法分為兩步，第一步將實驗數據分段，用最小二乘法分別辨識電機轉速為正和轉速為負時的摩擦靜態參數；第二步將轉速為零附近的預滑動區域作線性化處理，使其近似為二階系統，然后辨識該系統的幅頻特性，計算得到動態參數。

3.2.1 靜態參數的辨識

此時關節的輸出力矩主要克服摩擦力矩。

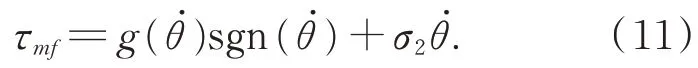
結合式（1）和（2），在電機空載勻速轉動的條件下，有：

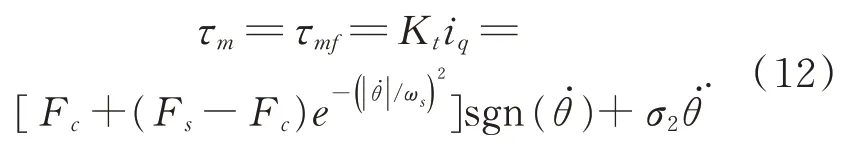
因此，可以測出電機在不同速度下勻速轉動時的q軸電流，乘以力矩系數Kt=0.21 N·m/A得到摩擦力矩，繪制摩擦力-速度曲線。

圖4 是摩擦參數辨識和補償平臺。關節空載且水平放置，計算機的TwinCAT 軟件用于控制電機勻速轉動，MATLAB 軟件用于數據的處理和分析。計算機和關節驅動板用網線連接，通信協議為倍福公司的EtherCAT。實驗時，采樣周期設置為5 ms，關節端速度變化范圍為-35（°）/s到-0.5（°）/s 和 0.5（°）/s 到 35（°）/s，每次改變0.5（°）/s，每個速度維持 15 s。為了消除電機在啟動和停止階段的電流波動，取中間5 s 的q軸電流值的平均值作為該速度下的電流值。根據式（12）計算出每個速度對應的摩擦力，用分段最小二乘法擬合摩擦力-速度曲線，結果如圖5 所示。

圖4 摩擦辨識和補償平臺Fig.4 Platform of friction identification and compensation

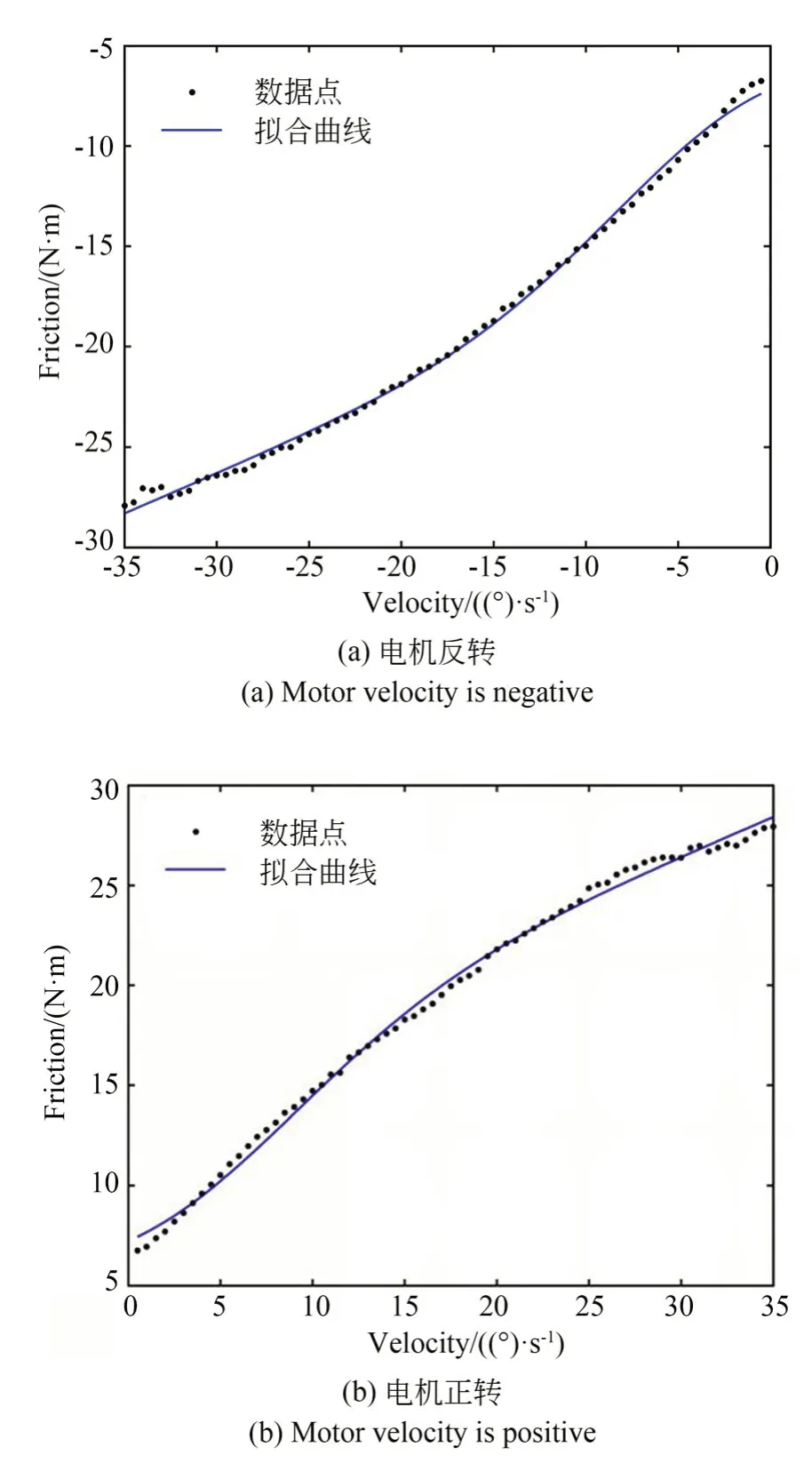
圖5 摩擦擬合曲線Fig.5 Fitting curves of friction torque

按照式（12）辨識的靜態摩擦參數如表1所示。

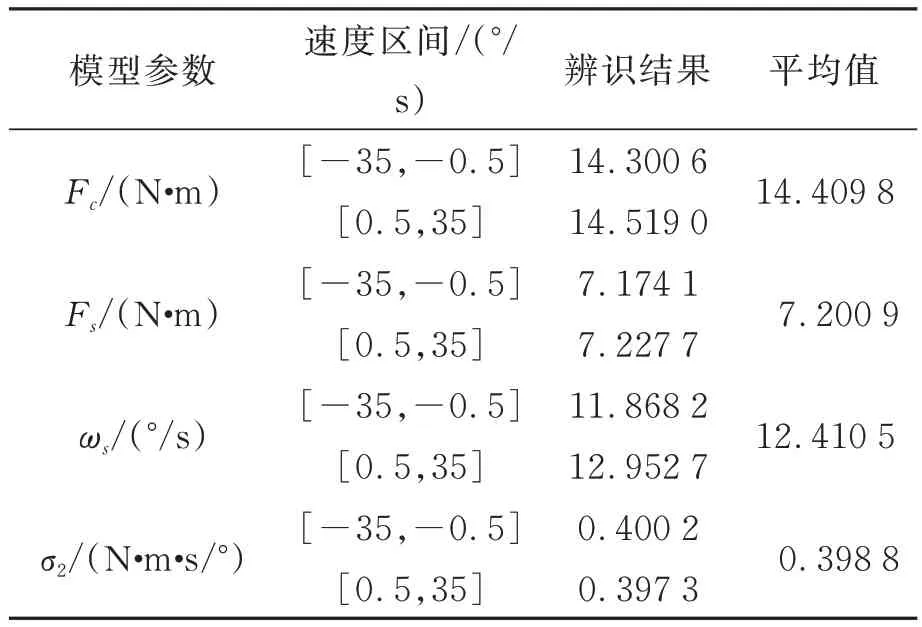
表1 靜態參數辨識結果Tab.1 Identification results of static parameters

3.2.2 動態參數的辨識

在電機的預滑動區域，即驅動力矩小于最大靜摩擦力矩時，對方程（7）在零狀態和零速度附近作線性化處理，即令得到：

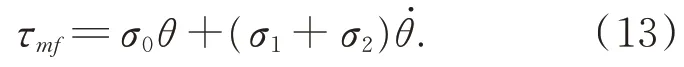
關節空載即τml=0 時，結合式（1）和（2），得到：

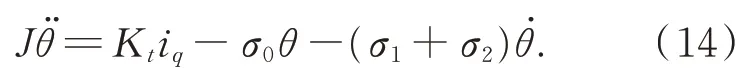
式（14）在頻域中的表達可寫成：

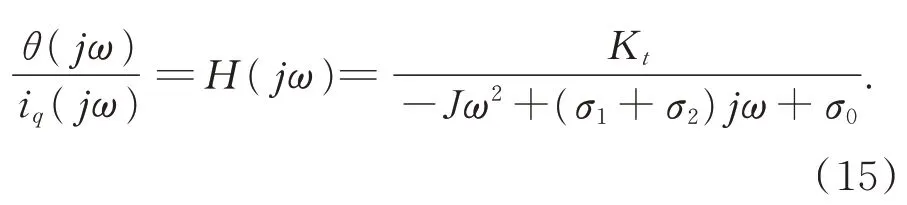
由此可見，在預滑動區域，LuGre 模型表現為帶有阻尼的質量-彈簧二階系統。可以通過偽隨機序列測試該二階系統的幅頻特性，分析伯德圖和擬合的頻響函數獲得動態參數σ0和σ1的估計值。

實驗時，以幅值為0.19 A，長度為511 位，周期為2 s 的M 序列作為q軸電流值輸入關節系統。該序列滿足準白噪聲要求，其自相關函數可近似為δ函數。序列幅值的均方根值對應的關節驅動力矩為6.65 N·m，小于最大靜摩擦力7.200 9 N·m，可防止系統離開預滑動區域。測量的系統響應為電機的轉角θ。為了排除非零初始條件的影響，輸入4 個周期的M 序列，測出后3個周期的系統響應并做平均處理。圖6 展示了其中一個周期的M 序列和系統響應曲線。

圖6 偽隨機序列和系統響應Fig.6 Pseudo-random sequences and system responses

用相關分析法將系統辨識為二階系統，得到頻響函數H(jω)。在ω=0 時，由式（15）得到：

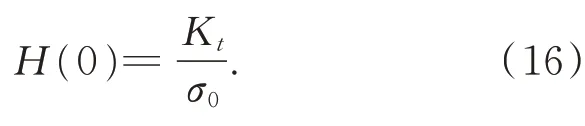
因此可以得到σ0的估計值。再根據式（15）計算σ1的估計值，辨識結果如表2 所示。

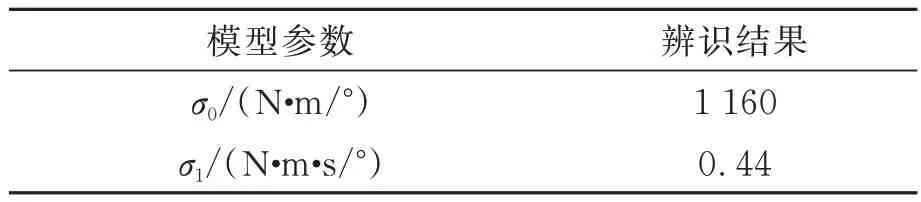
表2 動態參數辨識結果Tab.2 Identification results of dynamic parameters

3.3 基于灰狼算法的元啟發式辨識方法

灰狼算法（GWO）是一種新的元啟發式算法，靈感來自灰狼社會的狩獵行為。GWO 的種群代表一群狼，根據灰狼的適應度將其分為4 個階級：最優解稱為α 狼，次優解稱為β 狼，再次優解稱為 γ 狼，其余解稱為 ω 狼。

α，β和γ是搜索獵物的領導者，ω狼通過以下算子來更新它們的位置，以跟隨三只頭狼到達搜索空間的最佳區域：

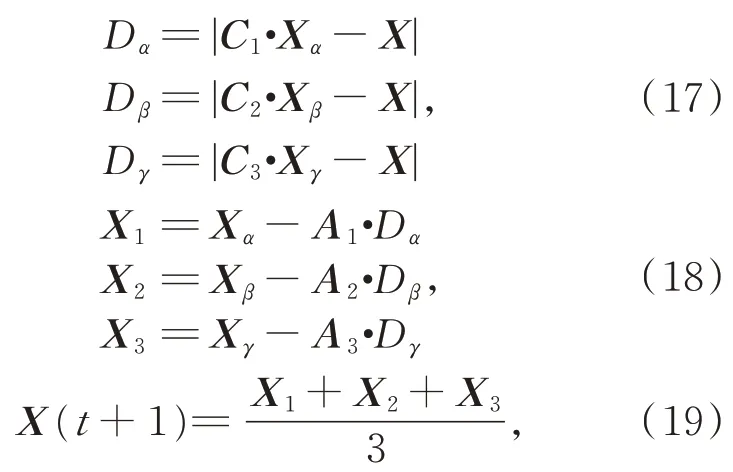
其中：Dα，Dβ和Dγ分別是狼群ω與頭狼α，β和γ的距離；X，Xα，Xβ和Xγ分別是狼群ω、頭狼α，β和γ當前迭代次數下的位置向量；X（t+1）是狼群ω下一次迭代的位置向量，t是當前迭代次數；Ai和Ci（i=1，2，3）是隨機生成的系數向量，如下所示：

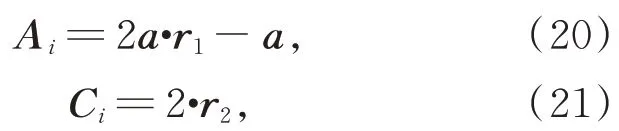
其中：r1和r2是區間［0，1］中的隨機向量；a的值在迭代過程中按照下式從2 線性減小到0：

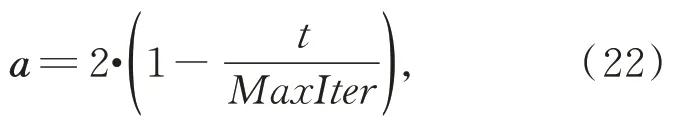
其中MaxIter是最大迭代次數。

圖7 展示了狼群如何在二維搜索空間內更新其位置。可以觀察到，最終位置將位于由搜索空間中頭狼α、β 和γ 所定義的圓內的隨機位置。換句話說，α、β 和 γ 估計獵物的位置，其他狼隨機更新至獵物周圍的位置。隨機向量Ai和Ci是該算法需要調節的兩個參數。|Ai|<1 時，灰狼會向獵物進攻，而|Ai|>1 時，灰狼會被迫逃離獵物，這允許灰狼進行全局搜索。|Ci|始終是區間［0，2］中的隨機值，它將提供隨機權重，以強化（|Ci|>1）或弱化（|Ci|<1）獵物在式（17）中定義距離的效果。Ci也可視為自然界中障礙物對灰狼接近獵物的影響，它有助于灰狼突破局部最優停滯。

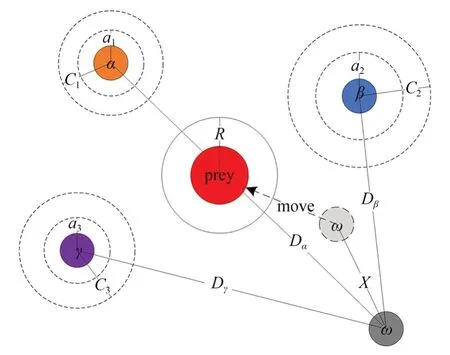
圖7 GWO 位置更新示意圖Fig.7 Position updating in GWO

在LuGre 摩擦模型的辨識中，該算法所處理的獵物是式（7）到（9）所包含的6 個參數。定義目標函數為：

其 中 ：N是 樣 本 數 ，fi和fdi分 別 是 第i次 采 樣 的模擬摩擦力和實際摩擦力。該問題是最小化尋優問題，即目標函數越小，灰狼的適應度越高。

圖8 展示了灰狼算法的操作流程。實驗時，參數約束設置為：Fc∈［0，20］，Fs∈［0，10］，ωs∈［0，20］，σ2∈［0，1］，σ0∈［0，30000］，σ1∈［0，1］，狼群規模設置為50。因為算法是隨機搜索的，故用不同的初始種群進行了10 次重復運算，并在200 次迭代后停止運行。圖9 展示了在不同的初始種群下，α 狼（最優解）的目標函數隨迭代次數的演變過程。

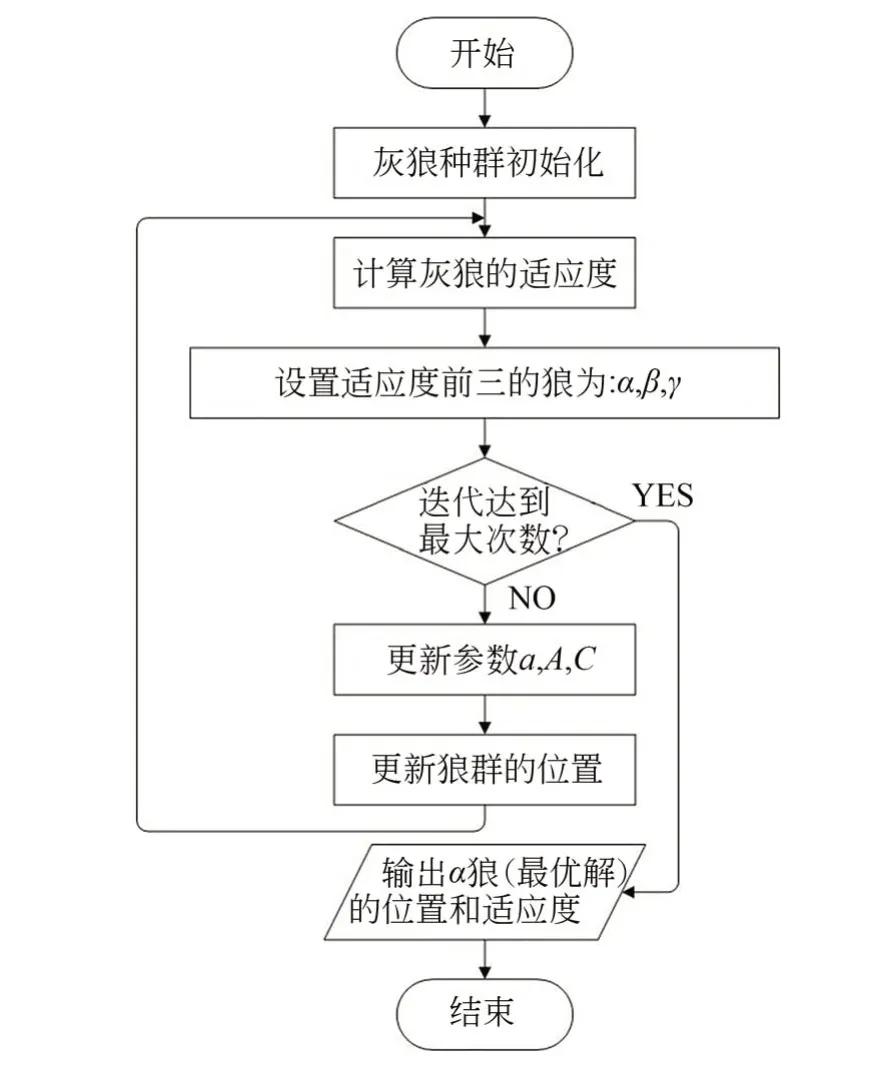
圖8 GWO 算法流程Fig.8 Flowchart of the GWO algorithm

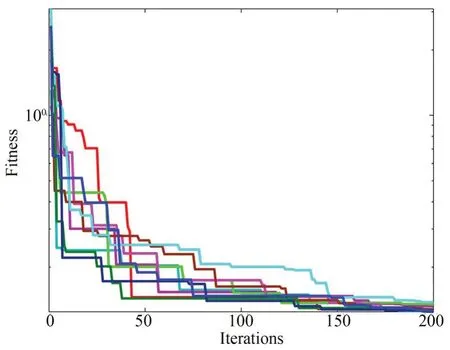
圖9 不同初始種群下GWO 的收斂曲線Fig.9 Convergence curves of the GWO algorithm with different initial population

可以看出，十次重復運行的結果都成功地收斂到最優參數附近，最佳運行的第38 次迭代和最差運行的第158 次迭代的目標函數都達到了10-0.84。一些運行在搜索過程中陷入了局部最優，但在最后的幾次迭代中都成功地突破停滯，走向全局最優。

基于灰狼算法的辨識結果如表3 所示。

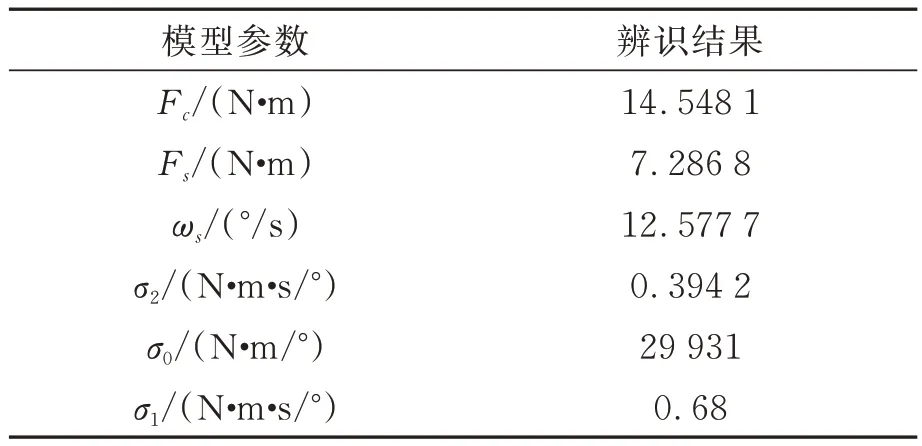
表3 基于灰狼算法的辨識結果Tab.3 Identification results of parameters based on GWO

3.4 兩種算法的對比

選擇式（23）作為辨識精度的衡量指標。J代表辨識結果和實驗數據之間的誤差，J越小，辨識精度越高。基于分段最小二乘法的一般辨識方法和基于灰狼算法的元啟發式辨識方法的對比如表4 所示。由此可見，灰狼算法的辨識精度高于一般辨識方法，且無需對實驗數據分段辨識，無需對預滑動區域作線性化處理，避免了建模誤差和計算誤差，在摩擦辨識領域具有更強的競爭力。

表4 兩種摩擦參數辨識算法對比Tab.4 Comparison of two friction parameter identification algorithms

4 摩擦補償及實驗

為驗證摩擦辨識的準確性，改善模塊化關節的動態性能，設計了圖10 所示的基于摩擦模型的前饋補償算法。關節仍采用位置-速度-電流三閉環控制，取期望的電機端速度值為摩擦補償器的輸入，按照式（7）到（9）計算相應的摩擦補償值τc，除以力矩系數得到補償電流值Iqc，作為前饋量疊加到電流環的輸入端，以消除摩擦擾動。

圖10 摩擦補償算法框圖Fig.10 Block diagram of friction compensation algorithm

關節輸出角度的跟蹤精度很大程度上取決于速度的跟蹤精度，因此取關節的角速度作為觀測量。實驗采用圖4 所示的設備，摩擦補償前，測得模塊化關節的速度環帶寬為12 Hz，實驗時，給定幅值為 1（°）/s，頻率為 10 Hz 的正弦關節端速度輸入信號sin（20πt），加入摩擦補償前后的關節端速度曲線、摩擦補償值曲線、速度跟蹤誤差曲線如圖11 所示。

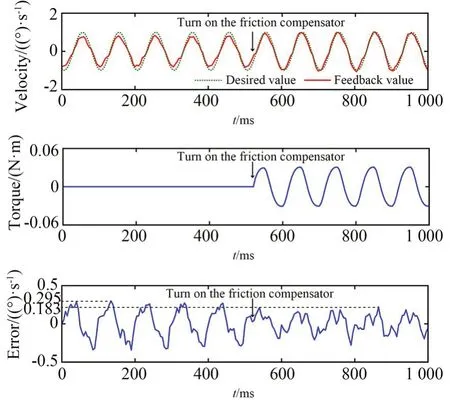
圖11 摩擦補償結果Fig.11 Results of friction compensation

圖11 中，在箭頭所標注的時刻開啟摩擦補償器，可以看到摩擦補償后，實線代表的速度反饋值能更好地跟蹤虛線代表的速度期望值，跟蹤誤差顯著減小，由補償前的峰值0.295（°）/s 減小到補償后的峰值0.183（°）/s，降低了38%。改變輸入正弦波的頻率，測得摩擦補償后，關節速度環帶寬為18 Hz，比補償前提高了50%。由此可見，建立的摩擦補償算法效果顯著，能提高速度跟蹤精度和速度環控制帶寬，同時驗證了摩擦模型辨識的準確性。

5 結 論

本文針對模塊化關節，設計了摩擦模型的離線辨識方法和摩擦補償算法。分別使用基于分段最小二乘法的一般辨識方法和基于灰狼算法的元啟發式辨識方法對LuGre 摩擦模型進行了參數辨識，并對辨識結果進行對比分析。設計前饋摩擦補償算法，以期望速度作為補償器的輸入，以補償的電流值作為輸出前饋給電流閉環。在模塊化關節上進行實驗，結果表明，相比于一般辨識方法，灰狼算法的辨識精度提高了19.2%；給定幅值為 1（°）/s，頻率為 10 Hz 的速度正弦輸入信號，摩擦補償后，關節速度跟蹤誤差減小了38%；摩擦補償后，速度環帶寬提高了50%。所提出的參數辨識方法準確有效，摩擦補償算法可以顯著提高關節速度跟蹤精度和速度環帶寬。