一種基于通道相位線性分析的直擴信號檢測算法

徐 哲，熊 剛

（1.中國人民解放軍91977 部隊，北京 100001；2.中國電子科技集團公司第三十研究所，四川 成都 610041）

0 引言

直接序列擴譜（Direct Sequence Spread Spectrum，DSSS）信號具有頻帶寬、抗干擾性能好、傳輸速率高和隱蔽性強等多種特點[1]，已經被軍事通信與民用通信領域廣泛采用，如無人機數據鏈通信系統、全球定位系統（Global Positioning System，GPS）、美國第三代國防衛星通信系統（Defense Satellite Communication System III，DSCS III）、跟蹤與數據中繼衛星系統（Tracking and Data RelaySatellite System，TDRSS）、碼分多址（Code Division Multiple Access，CDMA）通信和無線局域網（Wireless Local Area Network，WLAN）等[2]，由此低信噪比下DSSS 信號的檢測技術成為了頻譜監測、網電對抗等應用中的重要研究課題。直擴通信信號的存在性檢測為后續參數估計和解擴的前提，但在實際環境中電磁環境日益復雜，且可提供的目標信號先驗信息較少，可以視作近似盲檢測范疇。

由于DSSS 信號具有低功率譜和低工作信噪比的性質，其經常表現為淹沒在電磁空間噪聲里，導致很多傳統的檢測方法在運用于DSSS 信號時效果不理想。這個問題引起了眾多研究機構和學者的關注，例如文獻[3]中描述的方法都是基于已知DSSS 信號的周期特征和一些先驗假設條件的，否則無法檢測；文獻[4]是根據短碼DSSS 信號的符號循環平穩特進行檢測，不能用于長碼DSSS 信號。因此，現有研究的不足也對DSSS 信號的檢測算法分析及改進提出了較高要求[5]。

針對上述問題，本文提出了一種DSSS 信號的檢測新方法，該算法具有檢測率較高，且不需要太多的目標先驗信息的特點。該方法基于對接收的DSSS 信號頻域空間協方差矩陣優化計算思路，能夠在低信噪比條件下正確檢測出DSSS 信號，穩健性強。此外，該方法通過對信號的交叉相位線性特征進行深入分析，實用性較好，能夠適用于長碼直擴、短碼DSSS 信號，可以實現成功的檢測。

1 信號模型分析

下面對本文研究的DSSS 信號目標對象系統和算法的數學模型進行說明。DSSS 信號的收發原理框圖如圖1 所示。

在通道下變頻、濾波和采樣處理后，接收到的DSSS 信號可以表示為：

式中：{d(kTc)}表示原始的信息符號；k為整數，k=1,2,3,…,n；{c(kTc)} 表示直接擴譜的碼序列；Tc表示擴譜碼間隔；S為DSSS 信號能量；{n(kTc)}表示信道高斯噪聲。擴譜碼序列可用{c1,…,cN}，ci∈{±1} 表示；相移鍵控（Phase Shift Keying，PSK）調制后得到的符號可用di表示，di∈{±1}。

短碼DSSS 信號和長碼DSSS 信號的區別為：短碼是在擴譜周期內僅調制一個符號碼元[6]；長碼是指對應于各個擴譜周期可調制多符號碼元。[7]長碼DSSS 信號的數學表達式為：

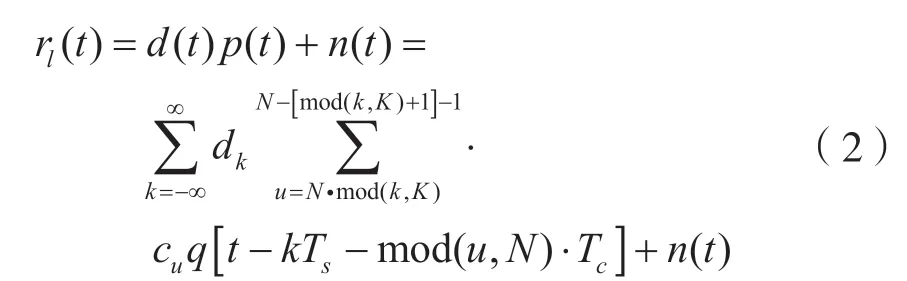
式中：dk表示擴譜符號序列，是獨立同分布的；n(t)為高斯噪聲；Ts為DSSS 信號的擴譜符號周期；cu（u=0.1,…,KN-1）表示其中的第u個碼元符號；Tc為符號長度，Tc=Ts/N；N表示長碼序列相對于符號的等分長度。長碼擴譜信號持續長度設為T0，則T0=KTs=KNTc；K表示數量，K=1,2,…,n。

在擴譜信號接收過程中，設濾波器的頻譜響應為G(f)，T表示擴頻周期，γ(f)表示信號的頻域變換，f表示頻率，當T取值較大時，DSSS 信號的平均功率表達式為：

其方差表達式為：

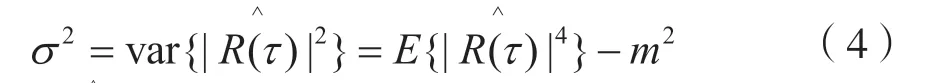
式中：R^(τ)表示信號的解析式，根據中心極限準則，R^(τ)服從高斯分布。

由于信號的高斯均值為0。當τ值較小時，可得到：

然后，對信號的檢測模型開展分析[8]。其二元假設檢驗的數學表達式為：

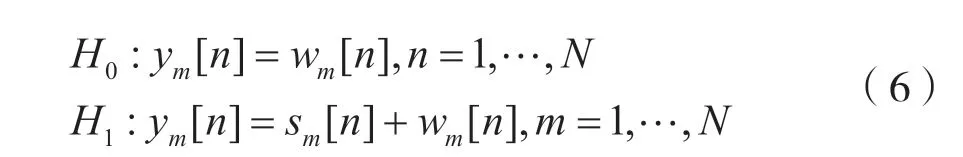
式中：H0和H1分別表示目標信號不存在和目標信號存在兩種情況；N表示接收的目標信號樣本數量。設w[n]表示在時間和空間上不相關的、白色的、零均值高斯噪聲，其方差為σ2。s[n]表示待檢測的目標信號，w[n]表示噪聲。

對于H1假設，如圖2 所示，DSSS 信號檢測可采用多通道結構[9]，使用M個處理單元組成的空間分布陣列來進行分析。其中，FFT（Fast Fourier Transform）表示快速傅里葉變換。

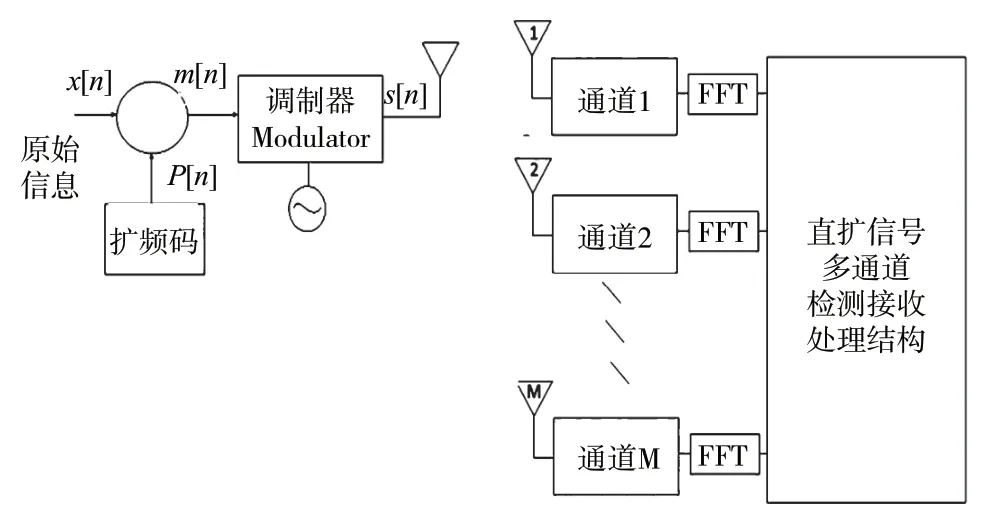
圖2 本文基于相位線性分析的DSSS 信號多通道檢測模型

從上圖中可看出，本文中設計的DSSS 信號檢測接收模型表達式為：

式中：m表示處理單元的序號；Dm表示第m個通道和參考通道之間的時間偏移量；x[n]表示基帶源信號；c[n]表示長度為L的長碼擴譜碼。對于長碼DSSS 信號，L通常應大于擴頻系數因子。式（7）的頻域變換計算式為：

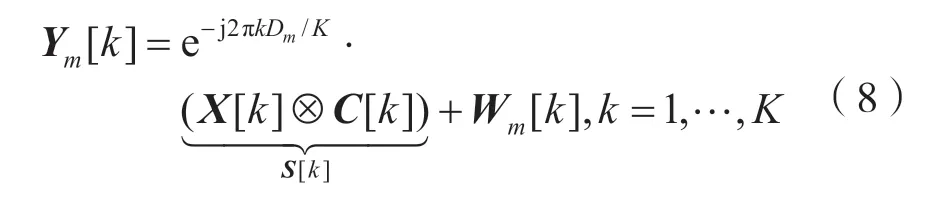
式中：k表示頻率譜線的索引值；K表示頻域譜線的總數量（K≤N）；?表示卷積。在頻域中M個通道的輸出向量可表示為：

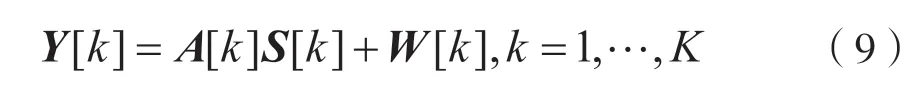
進一步得出，第k個頻域譜線的空間協方差矩陣可定義為：

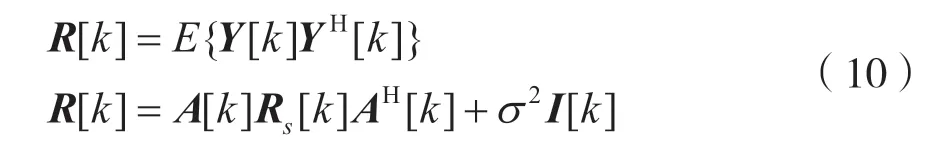
式中：(·)H表示矩陣的共軛轉置；A[k]代表流形矩陣；I[k]表示單位矩陣。設S[k]表示接收的單一寬帶DSSS 信號矩陣，則信號的協方差矩陣為：

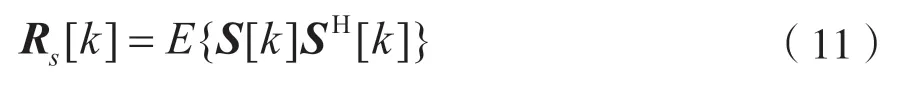
2 本文檢測算法分析

若存在DSSS 信號時，交叉通道協方差項的相位對應于信號帶寬是呈線性的[10]。圖3 和圖4 分別給出了交叉協方差項的幅度響應和相位響應。

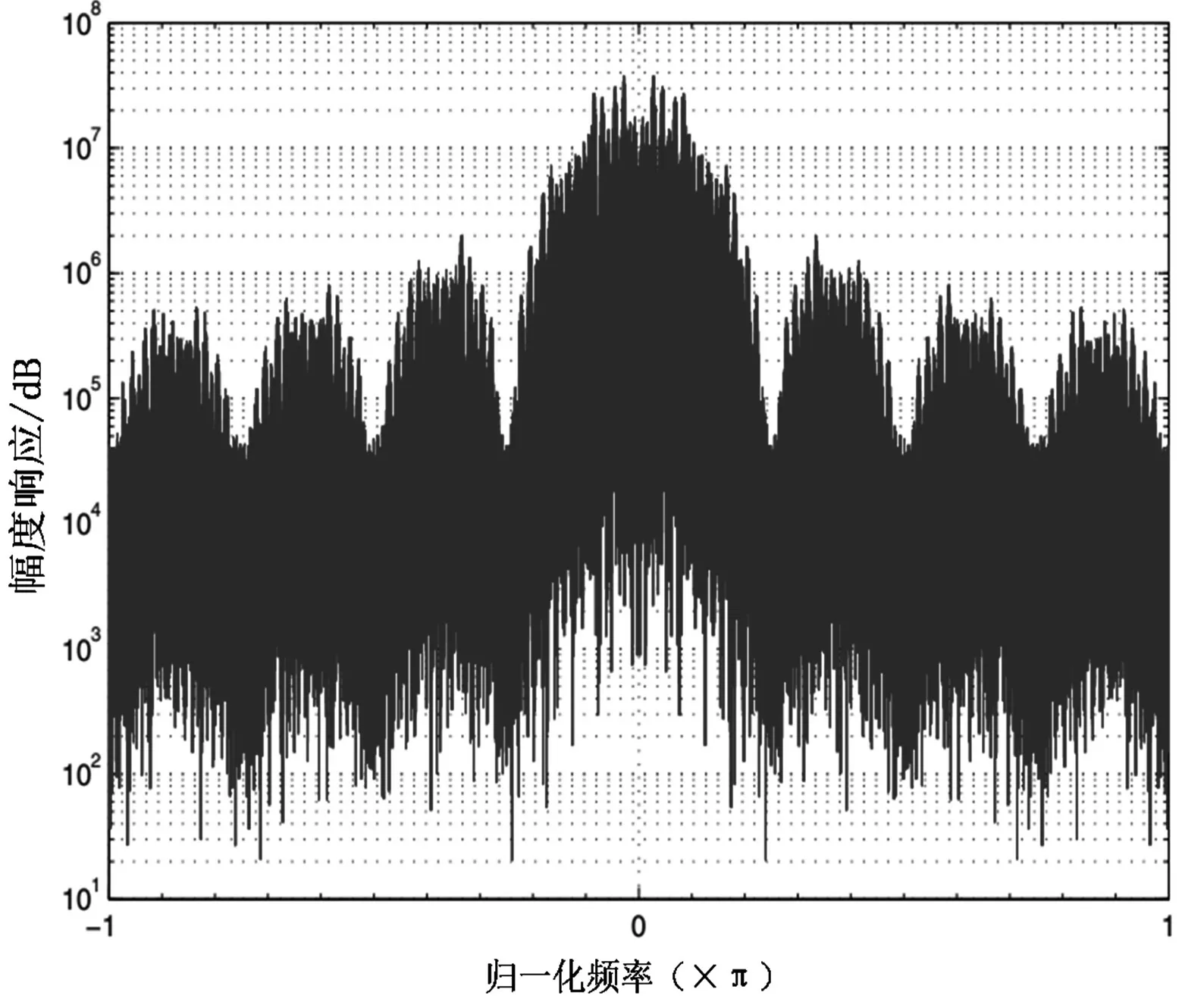
圖3 本文算法的交叉協方差項的幅度響應

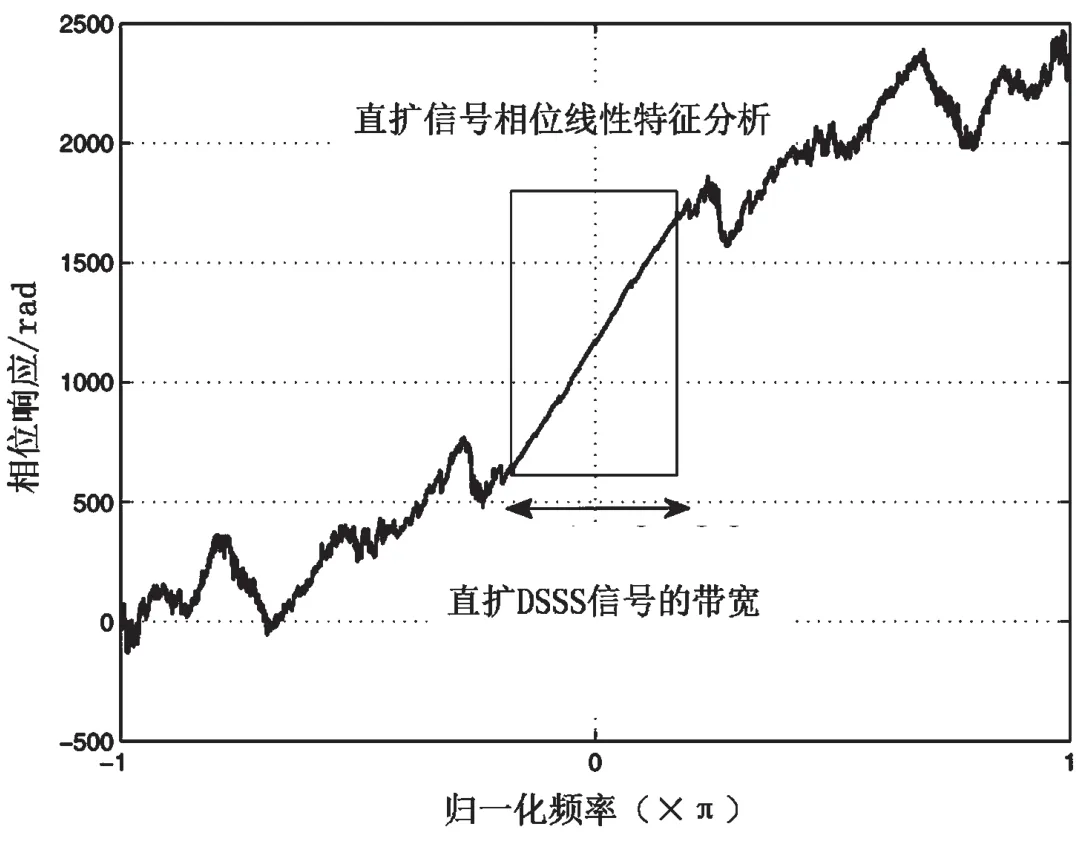
圖4 本文算法的交叉協方差項的相位響應

從圖4 中可以看出，DSSS 信號的空間協方差相位具有明顯的線性特征。

本文的檢測思路主要是通過先構建圖2 所示的多通道處理模型；然后對空間協方差矩陣進行計算，提取出空間分布通道的相位線性特征。在最小均方意義下，DSSS 信號的線性斜率與帶寬內的相位響應匹配，并對相位響應函數實現最佳擬合，從而提取出線性度特征。在DSSS 信號存在的情況下，線性擬合的曲線與信號相位是基本重合的，而在無信號存在，僅有噪聲的情況下，擬合偏差量較大。

DSSS 信號是寬帶信號，在低信噪比環境中常常被背景噪聲掩蓋；因此，本文對DSSS 信號的檢測采用了寬帶信號分解的思路，信號被分解成多個窄帶通道，然后處理窄帶內的各個信號，再將各頻帶的處理數據進行組合，得到最終結果。

（1）將DSSS 信號平均劃分為不重疊的多個通道子帶，其窄帶帶寬對應的快拍數為B；

（2）計算快照B時間內信號的離散傅里葉變換（Discrete Fourier Transform，DFT），得到如下空間估計協方差矩陣：

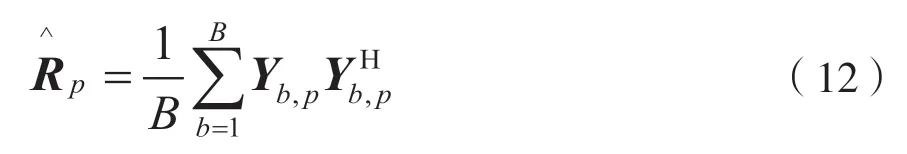
式中：B表示快拍數量，b=1,…,B；P表示每個快拍對應的頻率譜線的索引數，p=1,…,P；Yb,p代表第b個快拍，第p個頻率分量對應通道的輸出；進一步地，表示M×M維矩陣，且其協方差矩陣有P個。

（3）對于第p根頻率譜線，的交叉項相位值為：

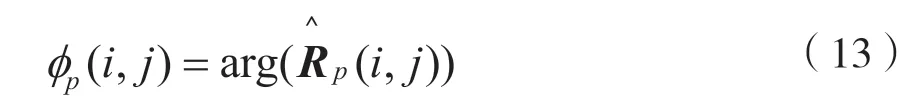
式中：矩陣的行索引用i表示，i=1,…,M-1；列索引用j表示，j=2,…,M，i＜j。從而φp(i,j)可由P個頻率分量和相位響應得出。信號帶寬對應的交叉信道協方差項相位響應如圖4 所示。當檢測出DSSS 信號時，相位響應曲線對于信號帶寬內的部分都呈現線性特性。

（4）通過使用線性模型，可將全部頻率譜線對應的相位響應函數實現曲線擬合，得到線性模型的數學表達式為：

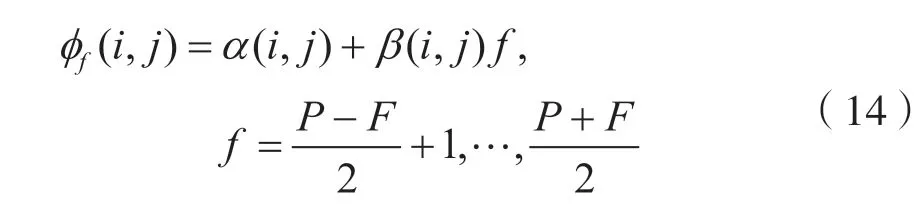
式中：F表示全部的頻率譜線集合變量；f表示頻率譜線索引；α(i,j)表示初始點；β(i,j)表示擬合曲線斜率。從信號中心頻率的兩側對稱地選擇信號帶寬內的F頻點（F＜P）。式（15）中表示的模型也可以用第i個、第j個交叉項協方差矩陣表示為：

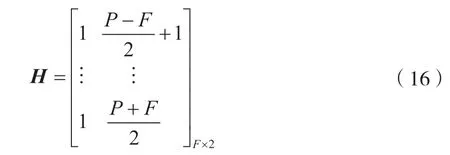
且有θ(i,j)表示未知參數向量，θ(i,j)=[α(i,j),β(i,j)]T；因此，各交叉項的擬合曲線參數可得出的數學估計表達式為：

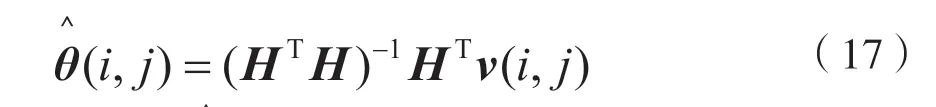
基于通道相位線性分析的DSSS 信號檢測方法的主要處理思路步驟為：

（1）計算所有交叉信道協方差項的相位響應和最佳擬合曲線之間的線性度偏差。為定量提取特征，可采用標準化的總均方根誤差，計算方式為：

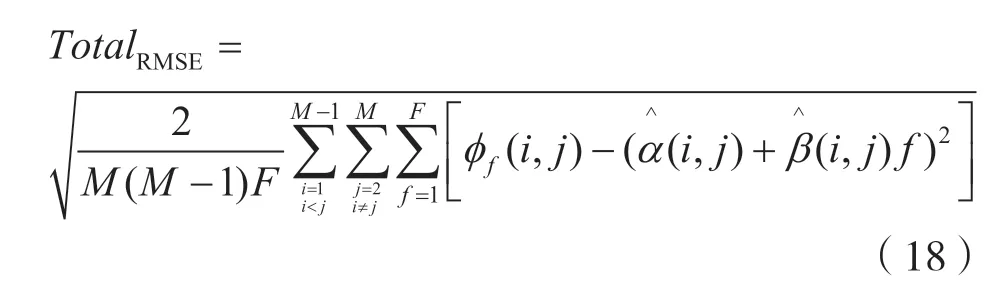
（2）采用式（18）中的總誤差作為檢驗統計量，即各通道的信號相位響應與擬合曲線之間的線性度偏差量。

（3）根據均方根值的分布選取合理的檢測閾值γthreshold，判決是否存在直擴DSSS 信號，如下所示：

γthreshold也與標準正態分布表和虛警率（False Alarm Rate，FAR）有關。TotalRMSE的值是對基于相位空間協方差矩陣的度量，并不依賴于噪聲功率。

3 仿真分析

本節對本文算法進行MATLAB 仿真試驗驗證。

首先設置仿真參數：接收的長碼/短碼DSSS信號的采樣率為200 MHz，載波頻率為60 MHz，擴頻碼元速率為10.24 Mb/s，樣本點數取為8 192，擴頻碼為M 序列。Monte Carlo 仿真次數設為1 000 次，信道噪聲為高斯白噪聲。

其次，對本文設計的基于通道相位線性分析的DSSS 信號檢測算法開展仿真，并選用過去的一些方法思路包括功率譜檢測算法、基于倒譜的檢測法和本文新方法進行比較，檢測性能曲線如圖5所示。

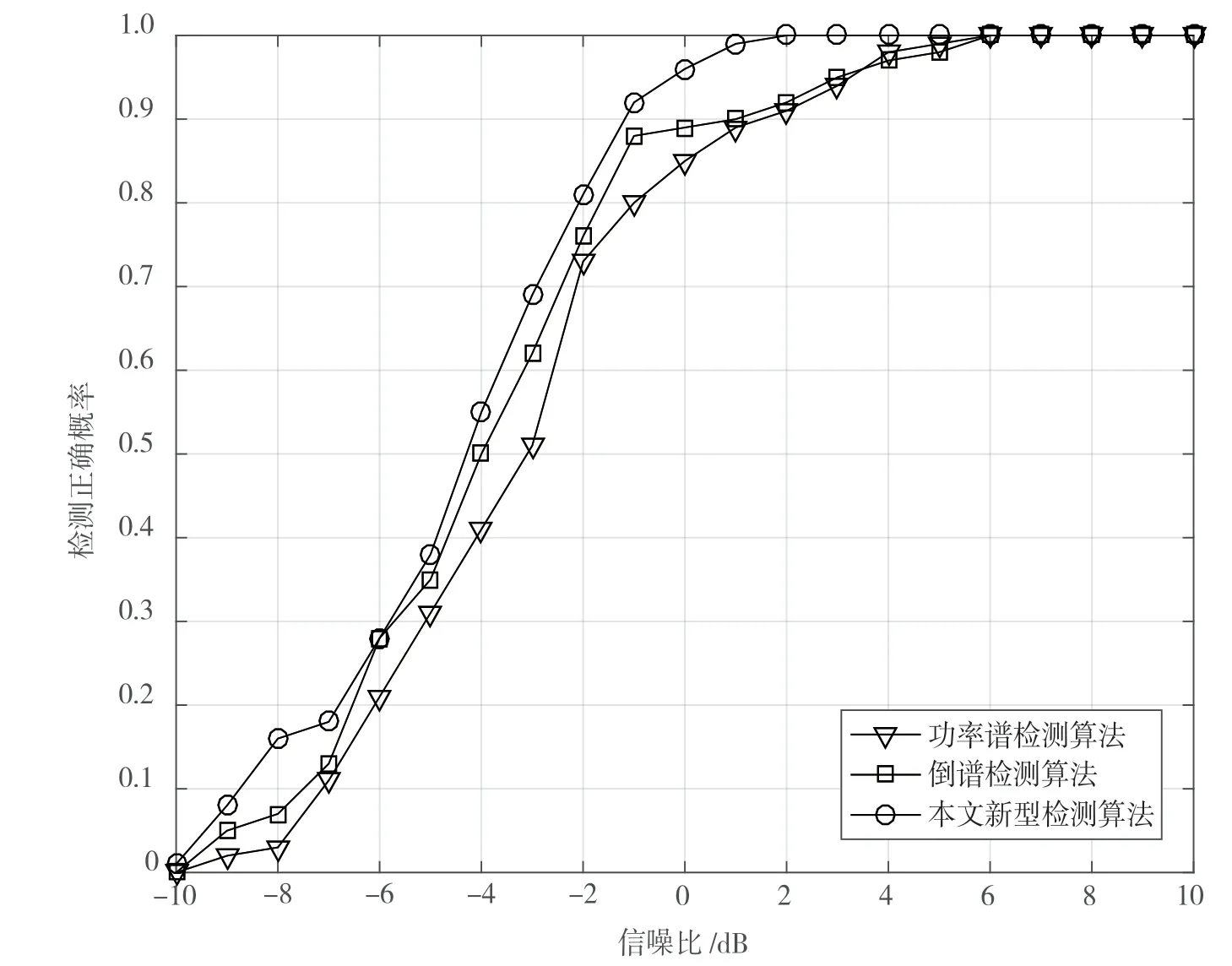
圖5 本文新算法與過去算法的性能對比曲線

分析圖5 可得出，本文的檢測算法可實現對DSSS 信號的正確檢測，且在低信噪比條件下，新方法的檢測效果相對優于過去的功率譜法和基于倒譜的檢測方法，性能有所提高。

4 結語

在低信噪比、復雜電磁環境中的DSSS 信號檢測問題一直是非協作信號處理研究中的難點問題，需要對過去的一些算法加以改進，并探索新的方法。本文提出了一種基于通道相位線性分析的DSSS 信號檢測算法。仿真試驗驗證了新方法的性能，比起過去的功率譜算法、倒譜算法等具有更高的檢測概率，相對更優，可為DSSS 信號的監測提供一種更有效的手段，并對網電對抗技術領域的研究提供參考。