分組碼的幾種碼限的討論

馮天樹

（北京科技大學天津學院，天津 301830）

0 引言

給定q元信息，位長k，增加m=n-k個監督編碼元，編碼為n長碼n(n＞k)，構成分組碼(n,k,d)或(q,n,k,d)。分組碼用符號(q,n,k,d)表示，包括線性分組碼和非線性分組碼。線性分組碼下文中也用符號[q,n,k,d]表示，是群碼，有封閉性和包含全0碼字。

設C是q元n長碼，即C是的子集。d是碼C的最小距離，表示為：

式中：d(x,y)表示x和y的漢明距離，即x和y不相同的位數。

如何構造(q,n,k,d)碼達到香農極限，一直是信道編碼工作者們追求的目標，科學家們在不斷地構造出新的好碼。在構造新碼的過程中，不可不免地遇到一個問題：哪些碼可以構造出來，哪些碼構造不出來，如果能構造出來，那么該如何構造？現在信道編碼理論中出現了分組碼的四個限或界（bound）：漢明限、Plotkin 限、Singleton 限，Gilbert-Varshamov 限。但所有信道編碼教材都對幾碼限介紹的非常簡潔，本文對這四個碼限進行詳細的討論和分析，希望對信道編碼工作者在構造達到香農極限的新碼時有所幫助。

1 幾種碼限

1.1 漢明限

1.1.1 碼限問題

漢明給出了分組碼(q,n,k,d)的d的一個上限，這就是漢明限[1]。漢明限為：

說明：

（1）漢明限是必要條件，不是充分的。所有的碼必須滿足此條件，不滿足的這條件的碼肯定不存在。

當式（1）取等號時的碼叫完備碼。令d=2t+1，參數為(n,k,2t+1)的q元完備碼滿足：

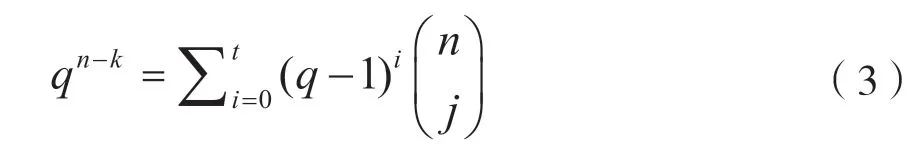
但遺憾的是滿足式（3）的q、n、k、d很少。

Golay 求出滿足式（3）的參數(q,n,k,d)的只有(2,23,12,7)，(2,90,78,5)，(3,11,6,5)三組；但Golay 發現二元(90,78,5)不存在[2]，只存在二元(23,12,7)碼和三元(11,6,5)碼。二元Golay (23,12,7)碼滿足：

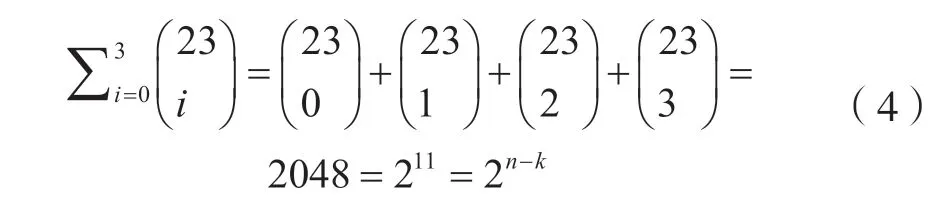
完備的線性分組碼只有以上幾種，后來數學家們找到一些非線性的q元完備碼[2]。

（2）q元(n,n,1)碼是完備碼，但毫無糾錯能力，沒增加任何校驗位。

（3）二元碼(2t+1,1,2t+1)奇數長的重復碼，是完備碼，許用碼組只有兩個碼：全1 碼、全0 碼。

（4）q元漢明碼的碼距d=3，是碼。q=2 時，為(2m-1,2m-1-m,3)，m=n-k是監督位個數。

（5）并不是任意給定q、n、k、d，都能構造出相應的(q,n,k,d)碼，使q、n、k、d滿足式（2）的約束。

對達不到漢明限的非完備碼，有個覆蓋半徑問題。

1.1.2 覆蓋半徑問題

[定義1]覆蓋半徑：碼集合C（許用碼組）是的子集，以每一個屬于C的碼v為球心，以ρ為半徑的球，對許用碼組的所有碼字做這樣的球，讓這些球并集等于。最小的ρ稱為碼C的覆蓋半徑，記為t(C)。

線性分組碼的t(C)實際上是編碼矩陣陪集首（或譯碼校驗子）的最大漢明重量[1]，即：

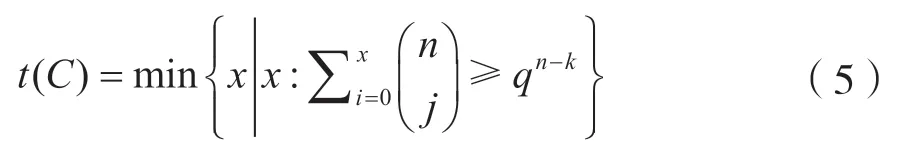
[定義2]每一個屬于C的碼v為球心，以ρ為半徑的球，所有球不相交的半徑ρ的最大值叫碼C的球半徑，記為S(C)。

顯然有：

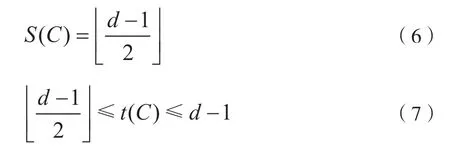
如果t(C)=S(C)，式（2）取等號，碼C就是完備碼。例如，漢明碼C的=1=S(C)，二元Golay 碼(23,12,7)的=3=S(C)。

對非完備分組碼C求覆蓋半徑t(C)，是一非常難的問題，數學家們一直在探索[3-4]，覆蓋半徑t(C)和相應的碼的碼重分布沒有對應關系，雖然線性碼的最小碼重等于最小碼距。

t(C)越小，空間中包含的許用碼組的碼字越多，越接近完備碼，因而t(C)越小的碼越好。但如何構造小t(C)的碼，人類仍然未知。

1.2 Plotkin 限

1.2.1 碼 限

Plotkin 也給出了線性分組碼[q,n,k,d]的d的一個上限，被稱為Plotkin 限[5]，碼限為：

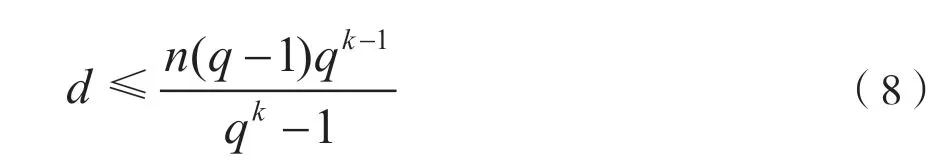
Plotkin 是根據同一[n,k]線性分組碼，有qk(n-k)個不同的生成矩陣；每個矩陣產生的許用碼組的總重量相同，為n(q-1)qk-1；每碼的非零最小碼重（最小碼距）不會大于平均碼重：。

對非線性分組碼(q,n,k,d)，M是碼字總數(對應線性碼的qk)，有如下結論：

證明思路是分組碼的總距離小于等于nM2(q-1)/q，再除以總碼子對M(M-1)。

式（8）的條件也是[q,n,k,d]碼存在的必要條件，分組碼必須滿足此條件。

1.2.2 等重碼

[定義3]等重碼：式（8）取等號時的碼叫等重碼或單純碼（simplex code），這時碼組的所有非零碼的碼重一樣。

線性等重碼的性質如下：

（1）可以證明[6]：q元等重線性碼[q,n,k,d]是q元漢明碼的對偶碼，對漢明碼m=n-k是監督位長度，對等重碼m是信息位長度。

（2）當q=2時，二進制線性等重碼[2m-1,m,2m-1]，碼 長n為2m-1，信息位數為m，校驗位數2m-1-m，許用碼組個數為2m，每個非零碼字的重量（碼距）是，例如，[3,2,2]、[7,3,4]、[15,4,8]碼等等。

（3）以等重碼所有許用碼為行構成碼矩陣，碼矩陣的列數比行數多一，即是(2m-1)×2m矩陣。

（4）因為等重碼的碼矩陣的列互換，碼的重量不變，那么碼矩陣列互換不影響碼重或碼距，生成矩陣列互換即可得到。

1.2.3 二元碼線性等重碼的構造方法

（1）方法1

先構造漢明碼，再用漢明碼的H矩陣做G矩陣即可生成等重碼。m（信息位個數）位二元共2m個組合，去除全0 碼，剩下的2m-1 列構成的矩陣就是等重碼的生成矩陣。

也可用循環碼生成，xn-1=g(x)h(x)，單純碼的生成多項式是其對偶漢明循環碼的h(x)。

（2）方法2

將2m×2m階0,1 Walsh-Hardamark 矩陣(即 將普通±1 的Walsh-Hardamark 矩陣的1 變為0、-1變為1)，去掉全0 列，得到(2m-1)×2m矩陣即為許用碼矩陣[7]。

非線性等重分組碼這里不做討論。

1.3 Singleton 限

1.3.1 碼限

設Aq(n,d)表示長為n最小碼距為d的q元分組碼所能容納的碼字個數的最大值，即Aq(n,d)=max{M|存在分組碼(n,m,d),給定n,d}。

Singleton給出了分組碼(n,k,d)的Aq(n,d)的上限：

當分組碼為線性碼[n,k,d]時，d的上限為：

這時碼限與q無關。

式（10）和式（11）表示的極限叫Singleton 限。對線性分組碼，Singleton 的證明思路是：對線性分組碼，最小碼距是最小的非0 碼重，此時信息位不可能全0，至少一個1，而n-k位監督信息最多有n-k個1，所以最小的非0 碼重至少為n-k+1。

1.3.2 MDS 碼

[定義4]使式（11）等號成立的碼叫極大距離可分（Maximum Distance Separable，MDS）碼，此時達到Singleton 限.

對二進制線性分組碼，只有重復碼(n,1,n)奇偶校驗碼(n,n-1,2)及(n,n,1)碼，這三類碼是MDS 碼，叫平凡MDS 碼。2 ≤k≤n-2 的(n,k,d)MDS 碼叫非平凡MDS 碼。

對二進制線性碼，MDS 碼都是平凡MDS 碼，沒有非平凡的MDS碼。因為q=2時n=3，(3,1,3)，(3,2,2)碼都是平凡碼。

著名的里德-所羅門（Reed-Solomon，RS）碼q=2，n=q-1=2m-1 是非平凡多進制MDS 碼。

線性[n,k,n-k+1]MDS 碼的對偶碼是[n,n-k,k+1]碼，也是MDS 碼。

1.3.3 MDS 碼的猜想

設M(k,d)=max{n|存在(q,n,k,n-k+1)碼}

[命題1]如果q≤k，那么M(k,d)=k+1

q元分組MDS 碼猜想[8]為：

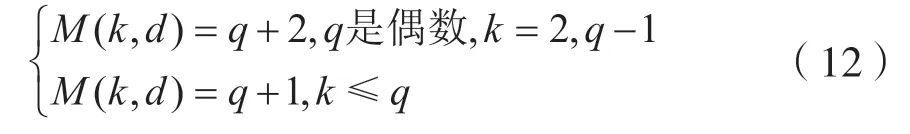
對線性碼，設m(k,d)=max{n|存在線性碼(q,n,k,n-k+1)}

這猜想至今沒被完整證明，只部分被證明，n、k、d是小數字時可以驗證。

1.3.4 多項式碼

[定義5]多項式碼：設a1,a2,…,an是Fq中n個不同的元素(n≤q)(1 ≤k≤n)，則集合：

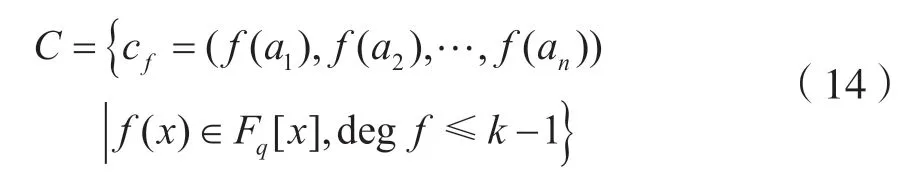
是q元[n,k,d]線性MDS 碼。

可以證明多項式碼的d=n-k+1，只要多項式的次數小于等于k-1,n≤q，則可構造一大類MDS 碼。擴展RS 碼是f(x)取固定某函數的特殊多項式碼，多項式碼提供了一大類構造MDS 碼的方法。

1.4 Gilbert-Varshamov 限

1.4.1 碼 限

Gilbert 用代數的方法證明分組碼(n,M,d)（不一定線性），如果存在下關系：

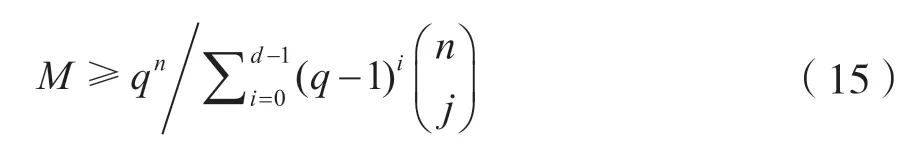
那么這樣的(n,M,d)分組碼一定存在。

如果線性分組碼[q,n,k,d]存在以下關系：

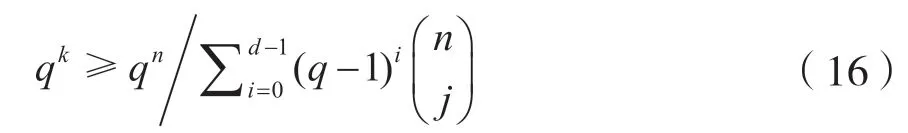
或者是：

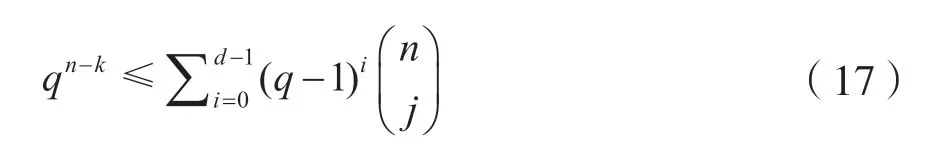
那么這樣的線性[n,k,d]碼一定存在，這就是Gilbert 限，該條件是碼存在的充分條件，不是必要的。

Gilbert 的證明思路：以許用碼的每碼字為中心，以d-1 為半徑的漢明球的并的集合個數，肯定超過的元素個數。

Varshamov 用概率統計的對線性分組碼方法證明了：

設q≥2，對每個，且0＜ε≤1-Hq(δ)，那么一定存在(n,k,d)碼

式中：R=k/n，δ=d/n，Hq(δ)是q元熵函數：

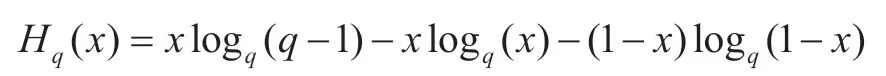
可以證明式（16）當n→∞時和（18）是一樣的，都稱Gilbert-Varshamov（GV）限。

式（16）叫非漸進GV 限，式（18）叫漸進GV 限。

1.4.2 碼限說明

式（16）這個限很松，給定n和k，d存在下限，或給定n和k，d存在下限。當n、k、d、q是小數字時，漢明碼、等重碼、RS 都比非漸近GV 限好；但比式（16）下限小的碼，是存在的。

[命題2]更緊的非漸進GV 限是：

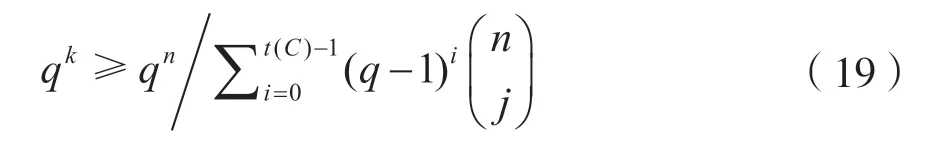
t(C)碼C的覆蓋半徑，所以求碼的覆蓋半徑很重要。證明略。

[命題3]對任意(n,k)線性分組碼，總存在d=1的碼。

證明：當生成矩陣的第k行為n長(0,0,…,0,1)或第k行有奇數個1 時，當發送信息為k長的(0,0,…,0,1)時，碼字為n長(0,0,…,0,1)，最小非0碼重為1，所以d=1。

[命題4]式（16）的等號，不可能存立，除非d=1。

證明：因為取等號時，以碼為球心以d-1 為半徑的球，會兩不相交，并覆蓋整個空間。這等效于：完備碼的以碼為球心以(d-1)/2 為半徑的球覆蓋整個空間，(d-1)/2=d-1，所以d=1。證畢。

2 4 種碼限的比較和說明

如圖1 所示是q=2 時的幾種限。

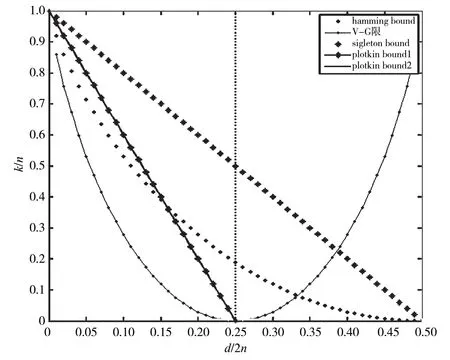
圖1 二進制碼限

圖1 中Plotkin bound2 曲線是：

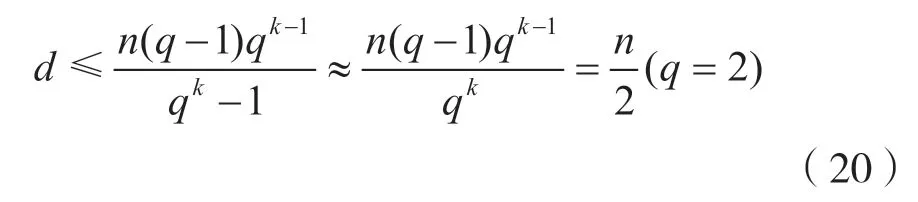
2.1 對幾種碼限的比較說明

2.1.1 說明一

在幾種上限（Plotkin、漢明、Singleton）中，任意一碼，只能滿足3個限中最小的。圖1中，R＜0.4時，碼限應小于Plotkin 限；R＞0.4 時，碼限應小于漢明限。意味著：想構造完備碼，R必須是大于0.4高碼率碼；想構造等重碼，必須R小于0.4。

例如：

二進制漢明碼(15,11,3) 碼，其Plotkin 限為dplotkin=7，其Singleton 限為dsingleton=4。

真實d=3 ＜dplotkin，d＜dsingleton。

二進制等重碼(15,4,8) 碼，其漢明限為dhamming=7，其Singleton 限為dsingleton=15-4+1=12。

因為，215-4＞C(15,0)+C(15,1)+C(15,2)+C(15,3)

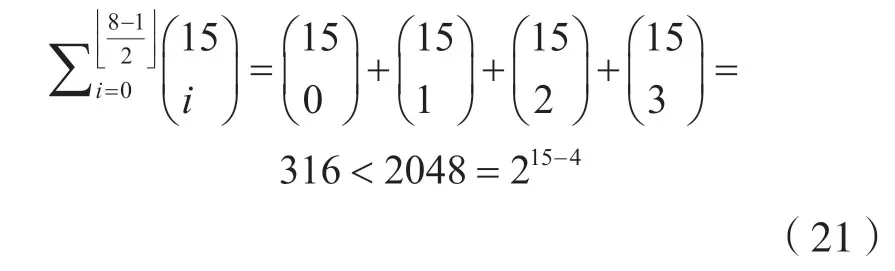
等重碼也是滿足漢明限。

二進制等重碼(15,4,8)碼在GV 限曲線的上面，則：

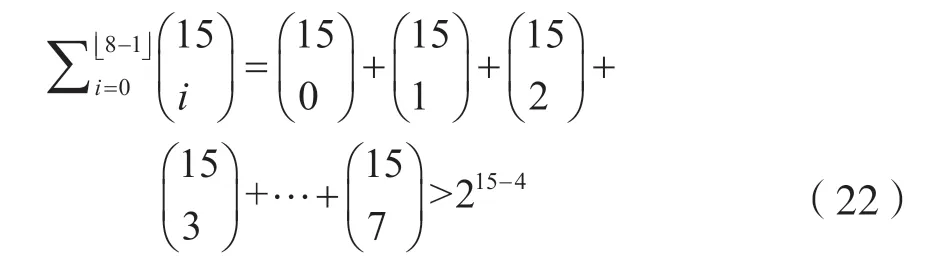
2.1.2 說明二

GV 限條件是充分條件不是必要的，分組碼可以位于GV限曲線的下面，并不是所有的碼都滿足GV限。

例如(15,4,5)碼：

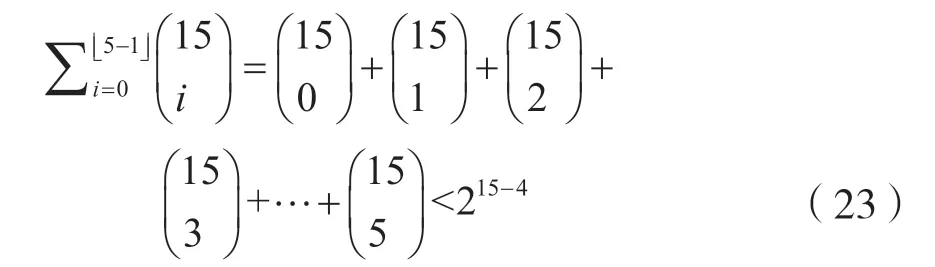
但該碼存在。

2.1.3 說明三

表1 是n=16 的所有k的二進制循環碼及其最小d。

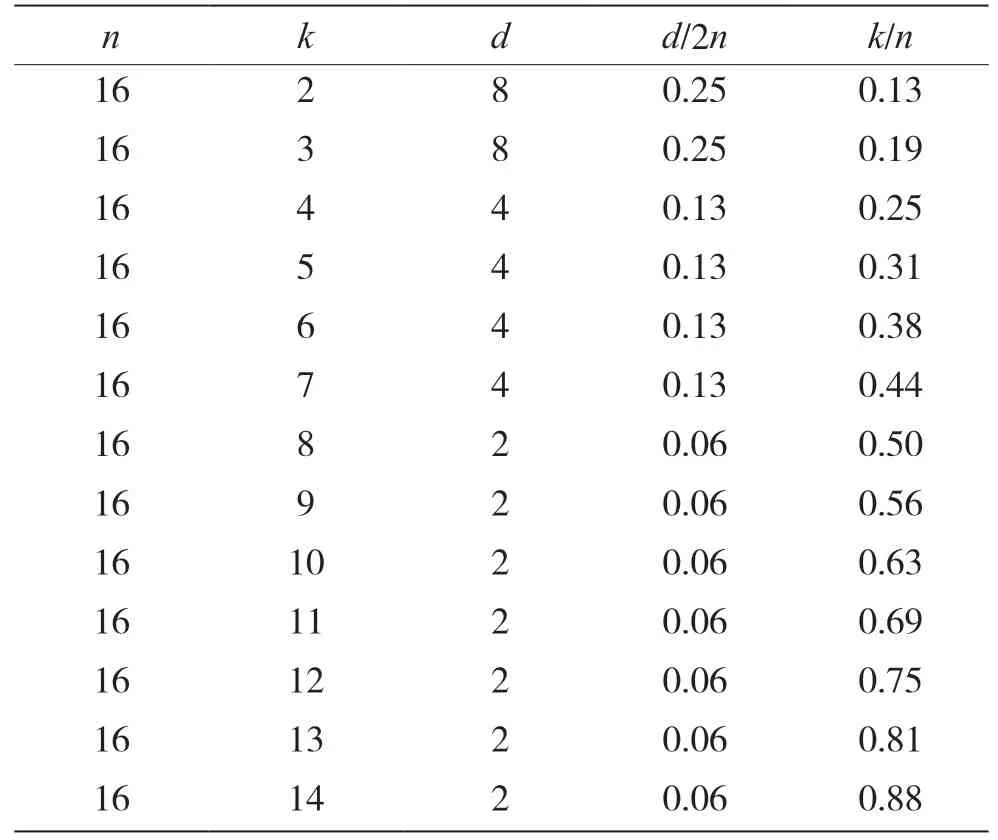
表1 n=16 的所有k 的二進制循環碼及其最小d 的碼限

圖2 是n=16 的所有k的二進制循環碼在碼限圖上的情況（小圓圈）。

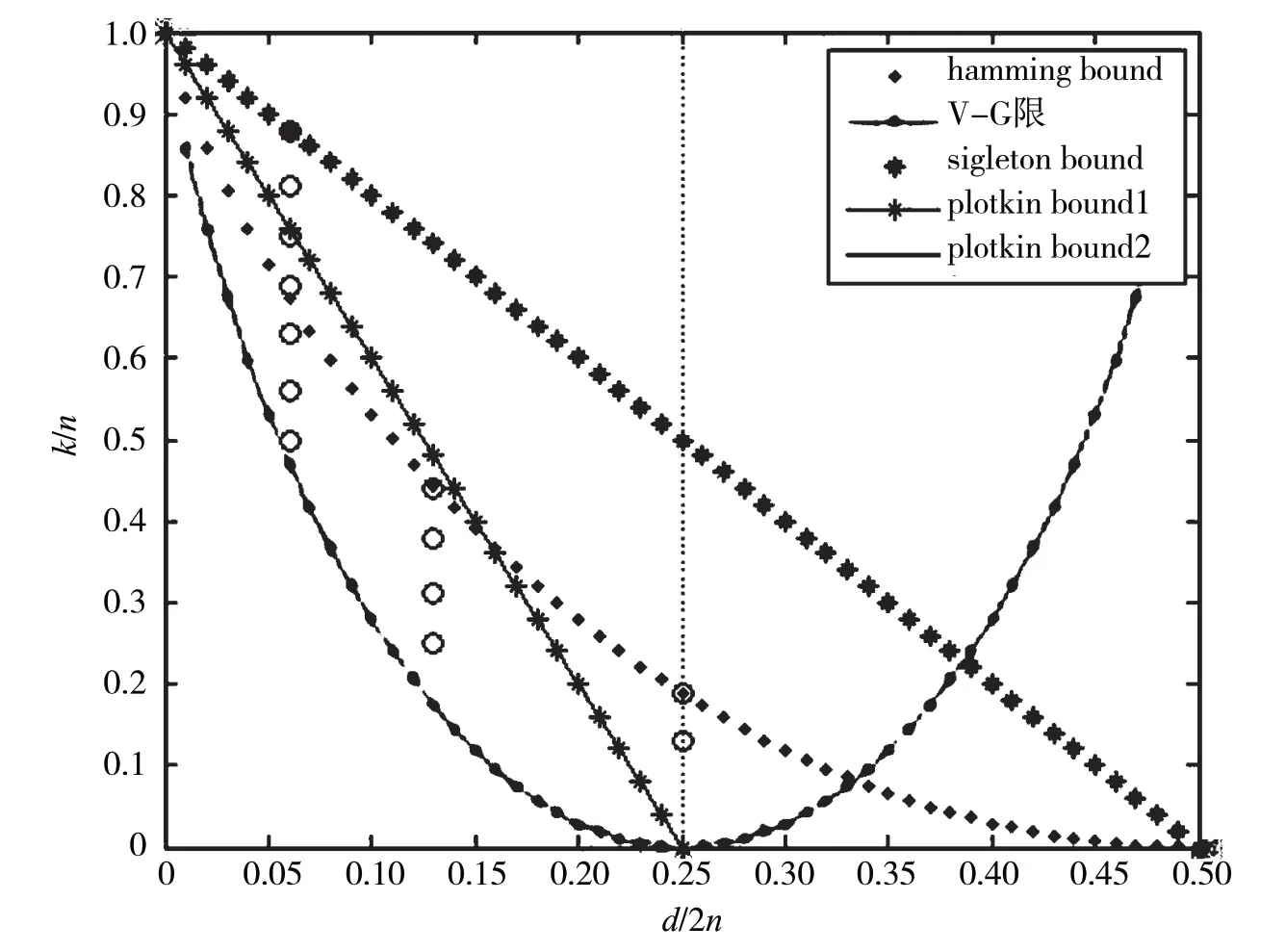
圖2 n=16 的所有k 的二進制循環碼及其最小d 的碼限

2.2 關于Singleton 限圖的一個問題的解釋

在圖1 的碼限圖中，Singleton 限曲線在漢明限曲線和Plotkin 限曲線的上面，而漢明限Plotkin 限是必要條件。讓人感到奇怪的是：達到Singleton 限的MDS 碼，怎么會滿足漢明限和Plotkin 限呢？下面舉例說明。

例如：RS 碼(7,2,3)(t=1,q=8)滿足漢明限。滿足Plotkin 限。

這是因為圖1 畫的二進制碼限圖，滿足Singleton 限的MDS 碼應是q進制碼（不是二進制），且必須滿足q＞n，而把Singleton 限畫在二進制碼限圖上（某些文獻也這樣畫Singleton 限曲線），就會產生誤解。

3 碼限對香農信道編碼定理的意義

香農給出了著名的信道編碼定理：在存在差錯概率的信道上，如果傳送碼率不超過信道容量C，那么一定存在一種糾錯編碼的方法，使接收端能夠無誤碼接收。香農信道定理的證明的方法是：隨機碼、碼長n無窮長和最大似然譯碼。

香農在信道編碼定理中使用隨機碼和n→∞時，當R=k/n＜信道容量C，那么平均誤碼率將趨近0。R＜C；但R不能趨近0，R越接近C，碼越好。

從上文中的幾個碼限可以得出，為達到香農限，不可能無限增加d，因為d的增大是受碼限約束的，并且d的增大對Pe的減少是有限的，為達到香農限只能想別的辦法。

[定義6]q≥2，設有一組{ni}i≥1，是一組遞增的分組碼長度，假設存在序列{ki}i≥1和{di}i≥1，使得存在q元分組碼Ci=(ni,ki,di)，那么碼序列Ci={Ci}i≥1是碼序列。C的碼率定義為：對漢明碼CH∶ni=2i-1，ki=2i-1-i，di=3，R(CH)=1，δ(CH)=0。

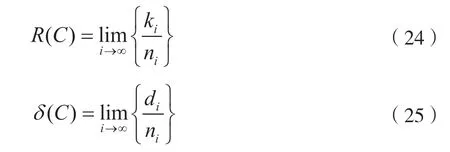
而構造香農碼要求：R＜信道容量C，要Pe→0，δ不能→0，否則沒糾錯能力。R不能→0，否則Pe→0 的代價不是在R略小于容量C時得到的。顯然漢明碼不能滿足香農定理的要求。

同樣，等重碼簇的R=0，δ=0.5，RS 碼簇、MDS 碼簇都不能滿足n→∞時，R和δ能同時保持大于0，不趨近0。

漸進GV 限，如式（18），對構造香農碼的意義：是否存在能用代數方法規則構造出來的碼，n→∞時R和δ能同時保持大于0，不趨近0。

所以數學家們在構造n→∞時R、δ都不趨近0 的碼。1972 年Justesen 構造出這種碼，但離漸進GV 限有點距離。

現在數學家們把碼空間的碼解釋為代數幾何中的影射空間的曲線，在構造漸進GV 碼如仙農碼方面有一定的進展[9]。

4 結語

本文對信道編碼中的分組碼的漢明限、Plotkin限、Singleton 限、Gilbert_Varshamov 限四種距離限進行了討論和分析，說明達到這些限時的碼的性質和碼的構造方法，并對這些碼限進行了比較和分析。結果說明：要降低誤碼率到達香農限，增加碼距的作用對是有限的，關鍵還是靠增加碼長和構造新的編譯碼方法。這些碼限特別是GV 限對構造香農理想碼有重要意義。這種思路和工程界構造的Turbo碼、LDPC 碼和polar 碼，不是一條思路。另外，分組碼還有Johnson限、Griesmer限、Elias-Bassalygo限，本文未做討論。