基于電磁感應加熱的硫化機熱板溫度場分析*

□ 孫國通 □ 陳 興 □ 王 進 □ 孫寶壽

1.寧波大學 機械工程與力學學院 浙江寧波 315211 2.浙江省零件軋制成形技術研究重點實驗室 浙江寧波 315211

1 研究背景

在用硫化機熱板加工橡膠制品的過程中,熱板表面溫度不均勻容易造成橡膠制品發生硫化不完全情況,嚴重制約最終產品的成型,成為制造瓶頸。傳統硫化機熱板采用油加熱或電阻加熱[1],加熱效率較低,且熱板表面溫度難以達到理想水平。電磁感應加熱控制方式簡單,在短時間內能產生大量熱量,成為當今加熱方式的研究熱點之一[2-3]。電磁感應加熱主要通過控制電磁感應過程中的電流、頻率來達到控制加熱的目的[4]。Eom等[5]研究發現,隨著電磁波頻率及電流的增大,硫化機熱板的溫差也增大。余露等[6]應用正交法對電磁參數進行優化,相對而言,電磁參數中電流的影響比較大,優化后熱板溫差為3 K。陳富豪等[7]結合遺傳算法與神經網絡,對感應頻率、感應電流密度、時間進行優化,得到最的優參數組合。趙朋成等[8]運用模糊控制原理控制感應過程中的加熱功率,改善熱板溫度的均勻性,同時確認由于電磁感應現象的復雜性,線圈的形狀對加熱所產生的影響也不容忽視。Huang Mingshyan等[9]提出使用分層式線圈,結合主成分分析及田口法來優化線圈的結構,可以將熱板的溫差控制在3 K以內。胡曉飛[10]研究得出,采用矩形線圈加熱熱板,溫度較均勻,同時推導得到熱板發熱區域與線圈形狀相關。Mrozek[11]發現磁屏蔽材料可以改善熱板上磁通密度的分布,以達到優化的目的,但并未解決如何排布屏蔽材料。

以上研究通過線圈設計、參數優化、添加磁屏蔽材料來解決熱板表面溫度均勻性問題。筆者通過采用COMSOL商業仿真軟件對電磁感應加熱下的硫化機熱板進行模擬仿真,分析噴涂不同尺寸及形狀45號鋼涂層時的加熱效率,研究如何選擇保溫電流,并采用溫度不均勻因數來評估熱板最終的溫差,為在電磁感應加熱下的硫化機熱板優化設計提供參考。

2 電磁感應加熱理論

電磁感應加熱源自法拉第發現的電磁現象,當線圈接通交流電時,在線圈周圍會產生交變磁場。在交流磁場中,金屬導體切割磁力線產生渦流,從而使導體內發熱。

2.1 電磁場控制方程

由積分形式轉換為微分形式的麥克斯韋方程組適用于所存在空間的任意一點,電磁感應加熱時的電磁場控制方程為:

(1)

式中:A為磁矢量,Wb/m;為梯度算子;J為總電流密度矢量,A/m2;Je為渦流密度矢量,A/m2;Js為源電流密度矢量,A/m2;σ為電導率,S/m;μ1為磁導率,H/m;t為時間,s;Φ為標量勢,V。

對式(1)取散度,得:

(2)

(3)

綜上得到熱板電磁場控制方程為:

(4)

對于熱板及線圈周圍空氣域,假設Je、Js為0,則控制方程為:

(5)

對于線圈,假設渦流可以忽略,則控制方程為:

(6)

2.2 溫度場控制方程

求解電磁場和渦流場的目的是利用電磁感應產生的焦耳熱作為內部熱源來計算溫度場。溫度場控制方程為:

(7)

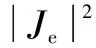
(8)

式中:ρ為材料密度,kg/m3;c(T)為比熱容,J/(kg·K);λ(T)為導熱系數,W/(m·K);qv為渦流引起的熱源強度,W/m3;T為熱板溫度,℃。

2.3 溫度場邊界條件

線圈與空氣交界面的邊界條件方程為:

-nair·(-λairTair)-ncoil·(-λcoilTcoil)=0

(9)

式中:nair、ncoil分別為空氣邊界和線圈邊界的法向向量;λair、λcoil分別為空氣和線圈的導熱系數;Tair、Tcoil分別為空氣和線圈的溫度梯度。

無窮域的邊界條件為:

T=T0

(10)

式中:T0為初始溫度,T0=25 ℃。

絕緣層的電荷量q為0。

熱傳導的邊界條件為:

(11)

式中:T1、T2為熱傳導兩側的溫度;λ1、λ2為熱傳導兩側的導熱系數;n為熱傳導法向方向。

熱板表面與空氣域邊界條件為:

=hw(Tα-T)+hm(Tα-T)

(12)

(13)

式中:nx、ny、nz依次為X、Y、Z方向向量;hm為熱輻射系數,W/(m2·K);hw為對流換熱系數,W/(m2·K);Tα為環境溫度模型,取25 ℃;ε為輻射率模型,取0.68;σs為斯特藩-玻爾茲曼常數。

2.4 電磁場邊界條件

模型域邊界可以分為兩類,一類是不同介質的界面,另一類是場的外邊界。

不同介質的界面邊界條件為:

(14)

式中:H1、H2為兩側磁場強度,A/m;B1、B2為兩側磁通密度,Wb/m2;n為單位法向量;t1為單位切向量。

場的外邊界在不同條件下有不同的邊界條件。通量平行邊界條件為:

A=0

通量垂直邊界條件為:

無限域邊界條件為:

A=0

在感應加熱的過程中,由于渦流的影響,在靠近線圈的熱板底部薄層中首先產生熱量,熱量的穿透深度δ為:

(15)

式中:f為交流頻率,Hz;ρ1為電阻率,Ω·m。

3 熱板溫度場分析

3.1 熱板物理模型

熱板電磁感應加熱模型如圖1所示,安裝位置如圖2所示。采用熱噴涂工藝在熱板上噴涂45號鋼涂層[12],為研究噴涂形狀對電磁加熱的影響,噴涂方式一般選擇菱形噴涂、全噴涂、三角形噴涂、仿線圈形狀噴涂、圓形噴涂、正方形噴涂。

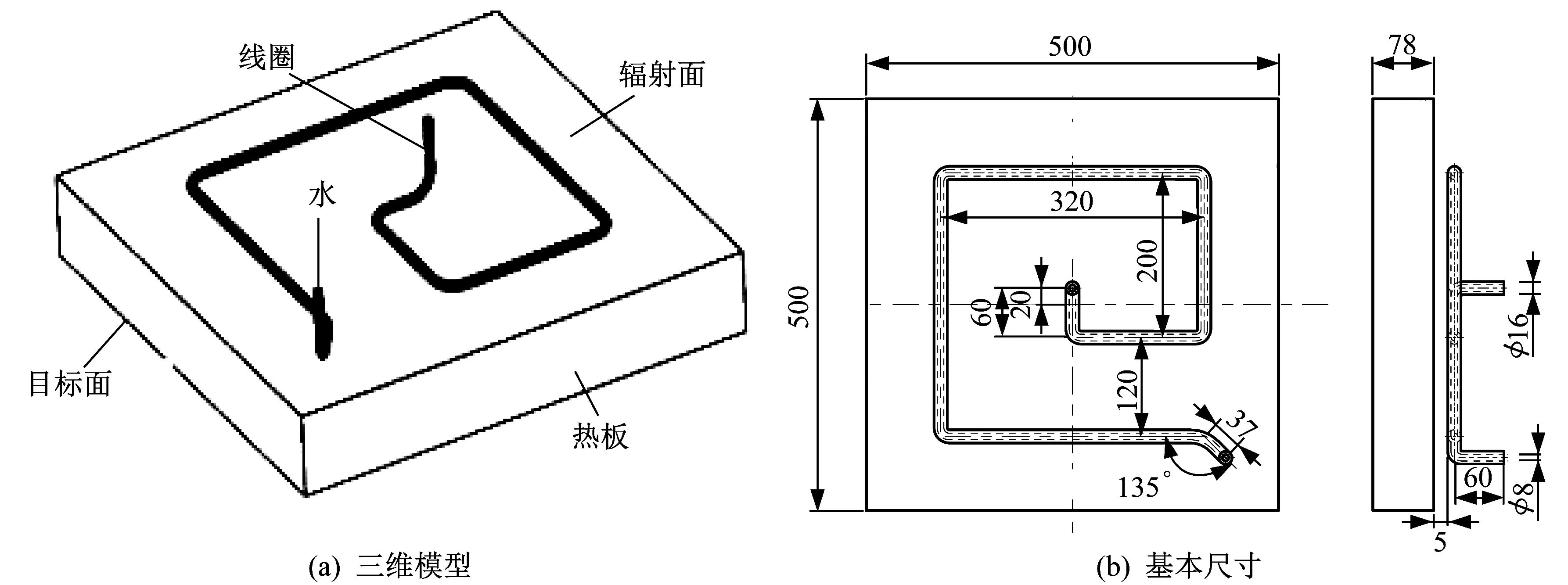
▲圖1 熱板電磁感應加熱模型

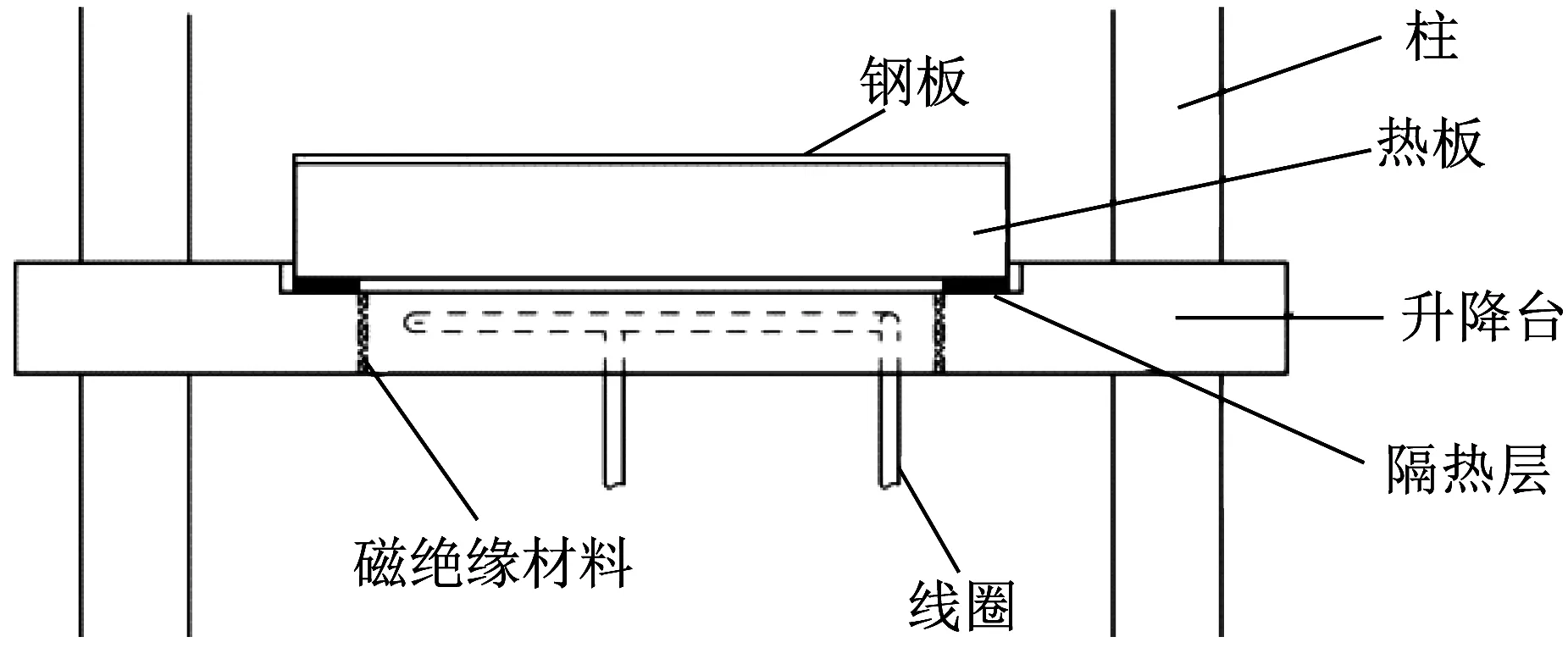
▲圖2 熱板安裝布置

在SolidWorks軟件中建立熱板三維模型,并建立六種噴涂模型,如圖3所示。

熱板平面尺寸均為500 mm×500 mm,線圈直徑為16 mm,冷卻管道直徑為8 mm,所使用的線圈與噴涂表面距離為5 mm。菱形噴涂尺寸為32 mm×32 mm,每個菱形噴涂間距為7 mm。全噴涂尺寸為320 mm×320 mm。三角形噴涂為等邊三角形,邊長為32 mm,每個三角形噴涂間距為7 mm。仿線圈形狀噴涂尺寸為46 mm。圓形噴涂直徑為32 mm,每個圓形噴涂間距為7 mm。正方形噴涂尺寸為32 mm×32 mm,每個正方形涂漆間距為7 mm。

根據式(15)可以得出,選用頻率為70 kHz時,在感應加熱過程中熱量的穿透深度為0.08 mm。由于穿透深度和頻率成反比,因此可選取較高的頻率。噴涂厚度需大于穿透深度,由此選擇噴涂厚度為0.3 mm。與文獻[13]介紹的傳統熱板不同的是,筆者在紫銅熱板頂面處額外增加2 mm厚的45號鋼鋼板,用于延緩溫度的迅速下降。

3.2 模型材料參數

模型中線圈及熱板材料為銅,涂層及熱板底面材料為45號鋼,所采用的材料屬性見表1。熱板溫度通常不高于300 ℃,因此不會使45號鋼涂層達到居里溫度。

表1 模型材料屬性

3.3 有限元模擬

根據以上分析,應用SolidWorks軟件進行熱板幾何建模后,將六種噴涂類型模型以.step格式文件導出,并在COMSOL Multiphysics軟件中依次導入文件,設置模型材料屬性,進行模型網格劃分,如圖4所示。感應電流為850 A,仿真頻率為50 kHz,線圈與熱噴涂涂層間距為5 mm,環境溫度為25 ℃,輻射率為0.68。

線圈在電磁感應加熱過程中,由于趨膚感應的存在,線圈外表面是感應電流的主要分布區域,在劃分網格時,需要對線圈的外表面進行集中網格細化處理。在COMSOL軟件中采用掃略網格對線圈進行網格劃分。硫化機熱板的工作區域形狀規整,此部分網格劃分采用六面體網格掃略。對于與線圈接近的熱板面,為保證仿真精度,需要進行額外細化處理。網格尺寸需小于熱板的趨膚深度。對于模型中的空氣域,由于區域形狀復雜,可以采用四面體網格來劃分。需要注意的是,因為線圈與熱板附近的空氣域接觸為曲面物理場,為保證有較好的計算精度和收斂性,需要進行網格細化處理。

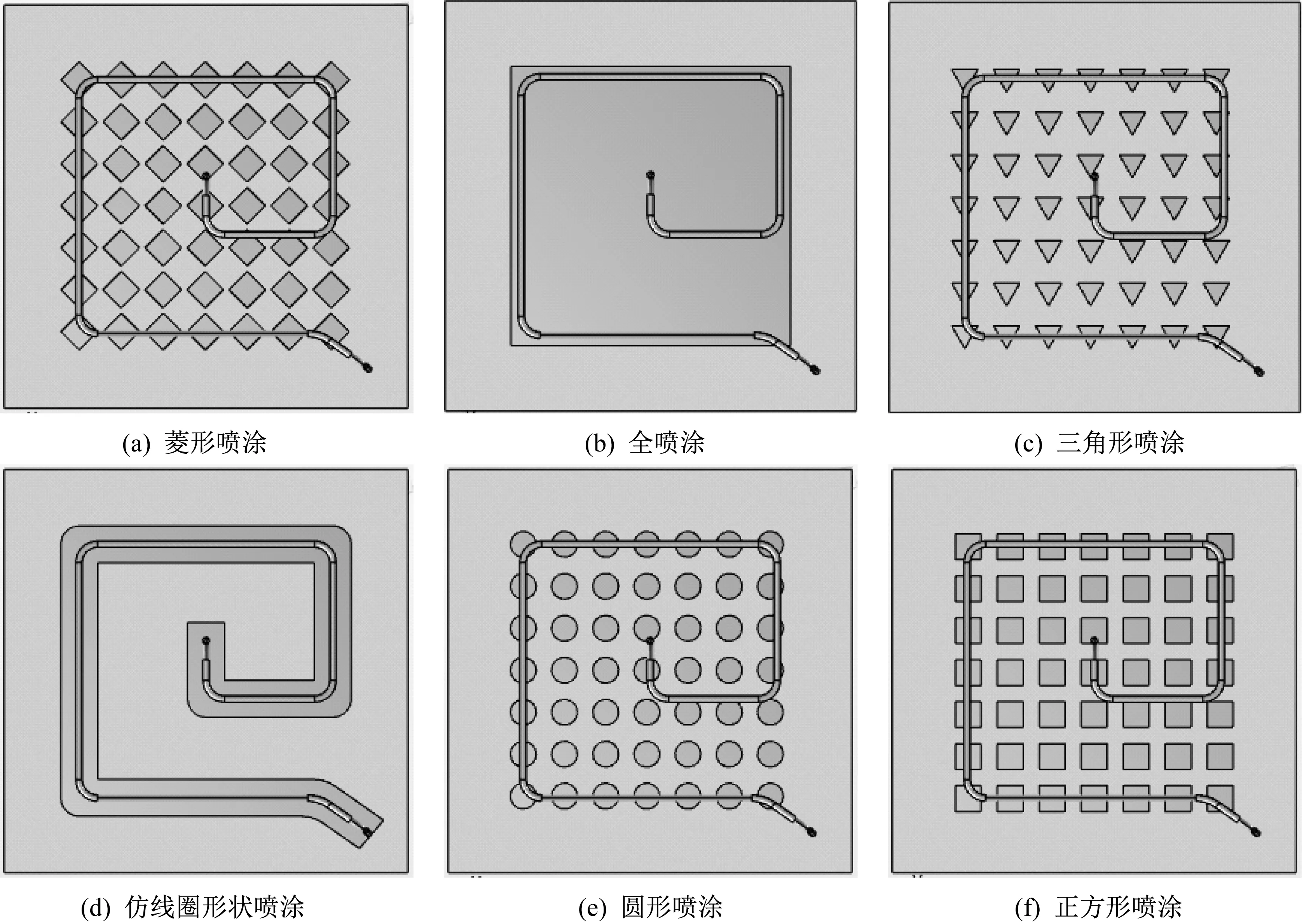
▲圖3 熱板噴涂模型

▲圖4 模型網格劃分

設置熱板目標面溫度為120 ℃,觀察熱板目標面溫度分布云圖及目標面溫差情況,分析在達到相同溫度120 ℃時六種噴涂方案溫升的速率及溫升過程中目標面溫度的均勻性。若電流一直保持在850 A,則熱板目標面溫度會隨加溫時間的延長而持續升高。過高的溫度會對硫化產品造成不利影響,如破壞硫化產品內部分子鏈破壞,硫化反原導致產品性能降低等。為使熱板在達到所需溫度時能夠保持溫度穩定,需要在目標面溫度達到120 ℃時及時減小加熱電流,進入保溫階段,并調整好保溫電流。此時熱板45號鋼涂層最高溫度會明顯下降,并逐步趨于穩定,熱板表面最小溫度與最大溫度的溫差也會隨著時間的延長而不斷減小,熱板的溫度達到均勻。由于保溫電流的影響相對獨立,因此筆者分析在加熱過程中如何合理確定保溫電流。

3.4 目標面溫度對保溫電流影響

仿真中,保溫電流和目標面溫度關系如圖5所示。

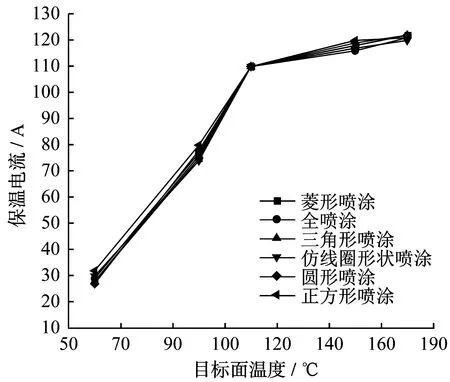
▲圖5 保溫電流與目標面溫度關系

由圖5可以發現,目標面溫度升高時,所對應的保溫電流增大。熱板目標面溫度升高時的熱量方程為:

QT=QE-QL

(16)

式中:QT為溫升時吸收的熱量;QE為渦流發熱量;QL為熱損失。

目標面溫度升高可分為兩個階段,第一是加熱階段,第二是保溫階段。第一階段中,隨著加熱電流增大,渦流發熱增加,溫升速度加快,此時熱板目標面最高、最低溫度的溫差也會增大。第二階段中,隨著保溫時間的延長,目標面最高、最低溫度的溫差逐步減小,并趨近于零。當QT為零時,式(16)變為:

QE=QL

(17)

此時目標面達到熱平衡,目標面溫度處于穩定,保溫電流僅起到維持熱板目標面溫度均勻的作用。如果目標面的目標溫度高,那么所對應的保溫電流需相應增大。由圖5還可以發現,當目標面溫度為60～120 ℃時,保溫電流變化斜率較大,保溫電流由30 A增大到110 A;當目標面溫度為120～180 ℃時,保溫電流變化斜率相對較小,保溫電流逐漸穩定在120 A。

3.5 溫度均勻性評估

引入溫度不均勻因數公式對目標面溫度均勻性進行評估,通過對熱板加熱后熱板目標面的溫度不均勻因數進行有效統計計算,量化熱板目標面溫度場分布的均勻性。目標面網格如圖6所示。溫度不均勻因數是目標面溫度標準差與目標面平均溫度的比值,反映的是熱板目標面達到目標溫度后熱板表面溫度的分布情況。通過加熱過程中熱板表面溫度不均勻因數的變化趨勢,可以評估熱板表面溫度均勻性。溫度不均勻因數Kt為:

▲圖6 目標面網格

(18)

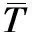
溫度不均勻因數越小,熱板目標面溫度的均勻性就越好。

3.6 溫度場分析結果

六種不同噴涂方案在電磁感應加熱3 000 s后熱板目標面的溫度分布云圖如圖7～圖12所示,溫度變化曲線如圖13～圖18所示。菱形噴涂方案在加熱時間達到2 220 s時,熱板目標面最高溫度達到初始設定目標溫度120 ℃。這一階段在噴涂層中產生渦電流,目標面溫度勻速上升。隨著加熱時間的延長,進入保溫階段。由于銅具有優良的導熱能力,使熱板目標面溫度快速上升,并使目標面溫度逐漸趨于均勻。進入保溫階段且加熱時間達到3 000 s后,熱板目標面最高溫度為120.100 ℃,最低溫度為119.648 ℃。全噴涂方案在加熱時間達到1 120 s時,熱板目標面最高溫度達到初始設定目標溫度120 ℃,然后調整加熱電流,在加熱時間達到3 000 s后,熱板目標面最高溫度為120.430 ℃,最低溫度為120.231 ℃。三角形噴涂方案在加熱時間達到1 410 s時,熱板目標面最高溫度達到初始設定目標溫度120 ℃,在加熱時間達到3 000 s后,熱板目標面最高溫度為122.878 ℃,最低溫度為117.898 ℃。仿線圈形狀噴涂方案在加熱時間達到710 s時,熱板目標面最高溫度達到初始設定目標溫度120 ℃,在加熱時間達到3 000 s后,熱板目標面最高溫度為121.128 ℃,最低溫度為120.950 ℃。圓形噴涂方案在加熱時間達到2 800 s時,熱板目標面最高溫度達到初始設定目標溫度120 ℃,在加熱時間達到3 000 s后,熱板目標面最高溫度為119.627 ℃,最低溫度為117.657 ℃。正方形噴涂方案在加熱時間達到2 220 s時,熱板目標面最高溫度達到初始設定目標溫度120 ℃,在加熱時間達到3 000 s后,熱板目標面最高溫度為120.957 ℃,最低溫度為120.658 ℃。

▲圖7 菱形噴涂方案溫度云圖

▲圖8 全噴涂方案溫度云圖

▲圖9 三角形噴涂方案溫度云圖

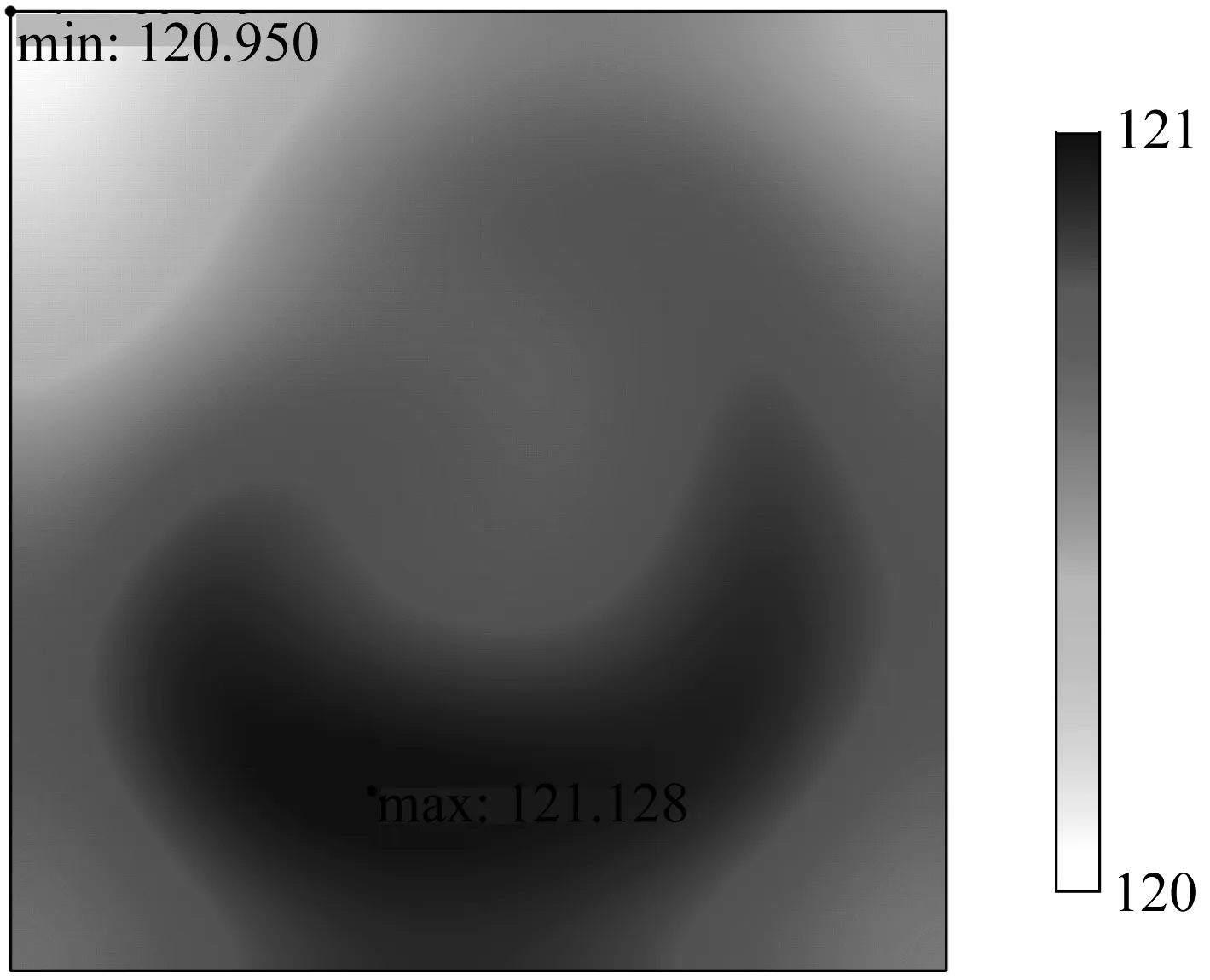
▲圖10 仿線圈形狀噴涂方案溫度云圖

▲圖11 圓形噴涂方案溫度云圖

▲圖12 正方形噴涂方案溫度云圖

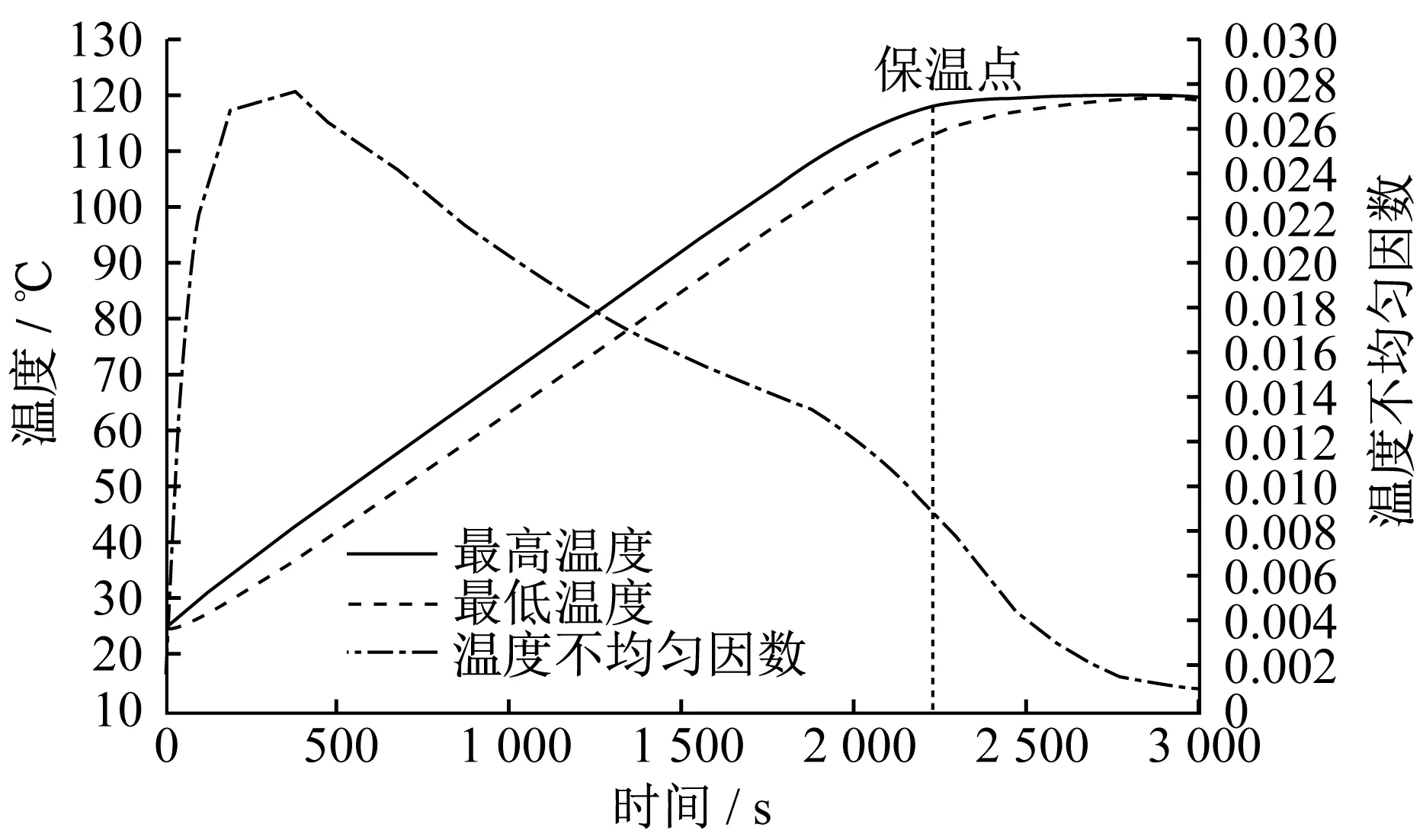
▲圖13 菱形噴涂方案溫度變化曲線

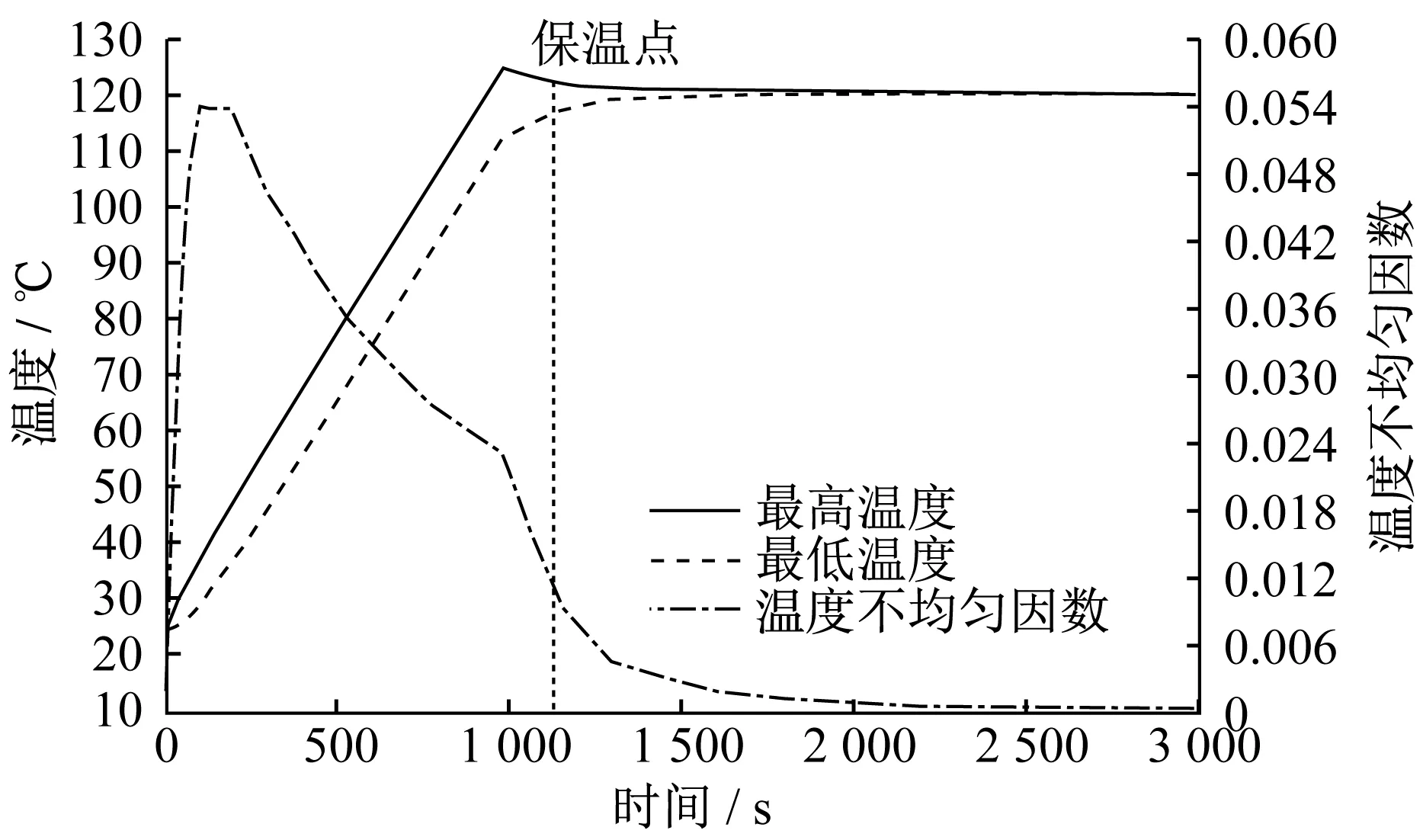
▲圖14 全噴涂方案溫度變化曲線

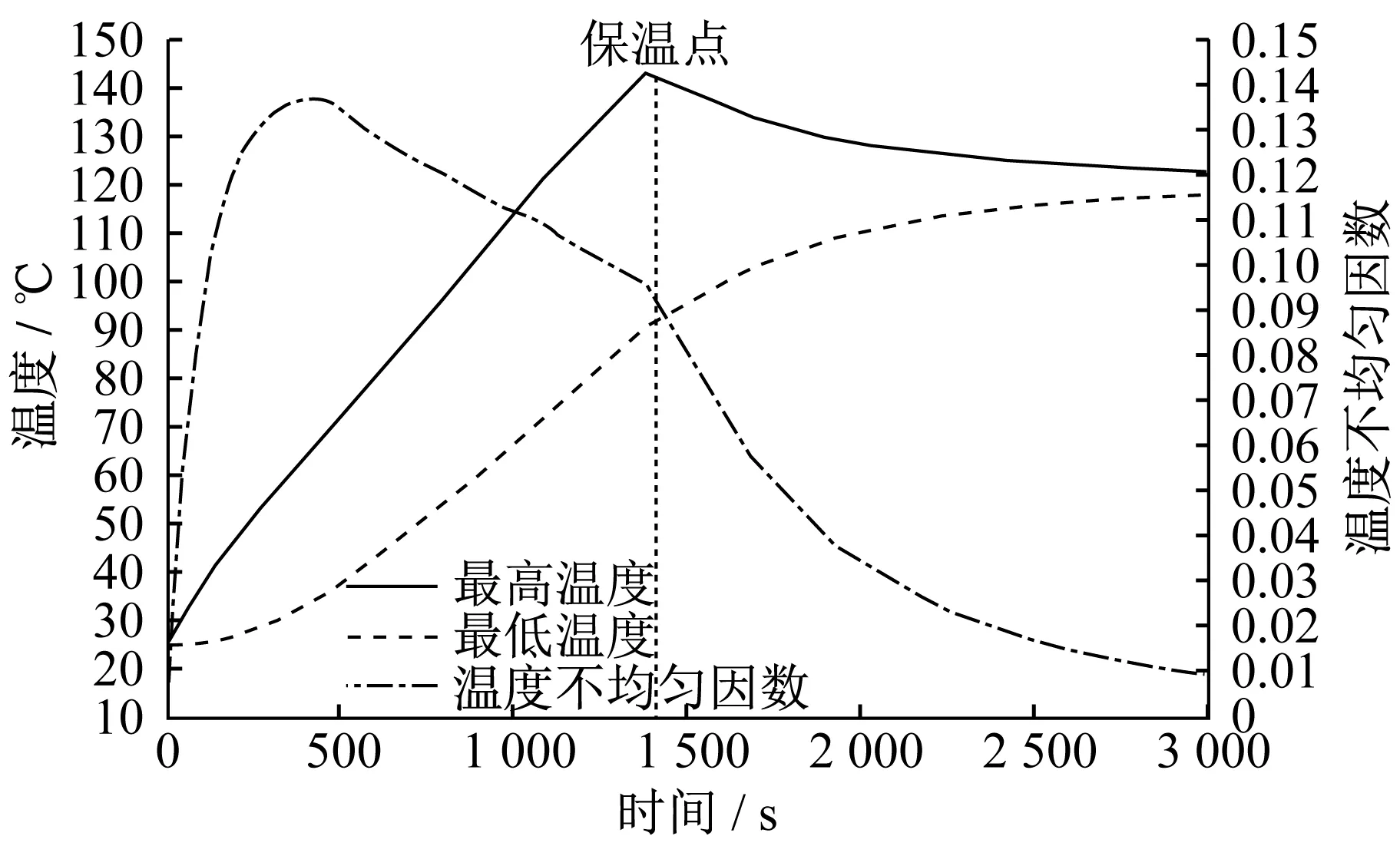
▲圖15 三角形噴涂方案溫度變化曲線

▲圖16 仿線圈形狀噴涂方案溫度變化曲線

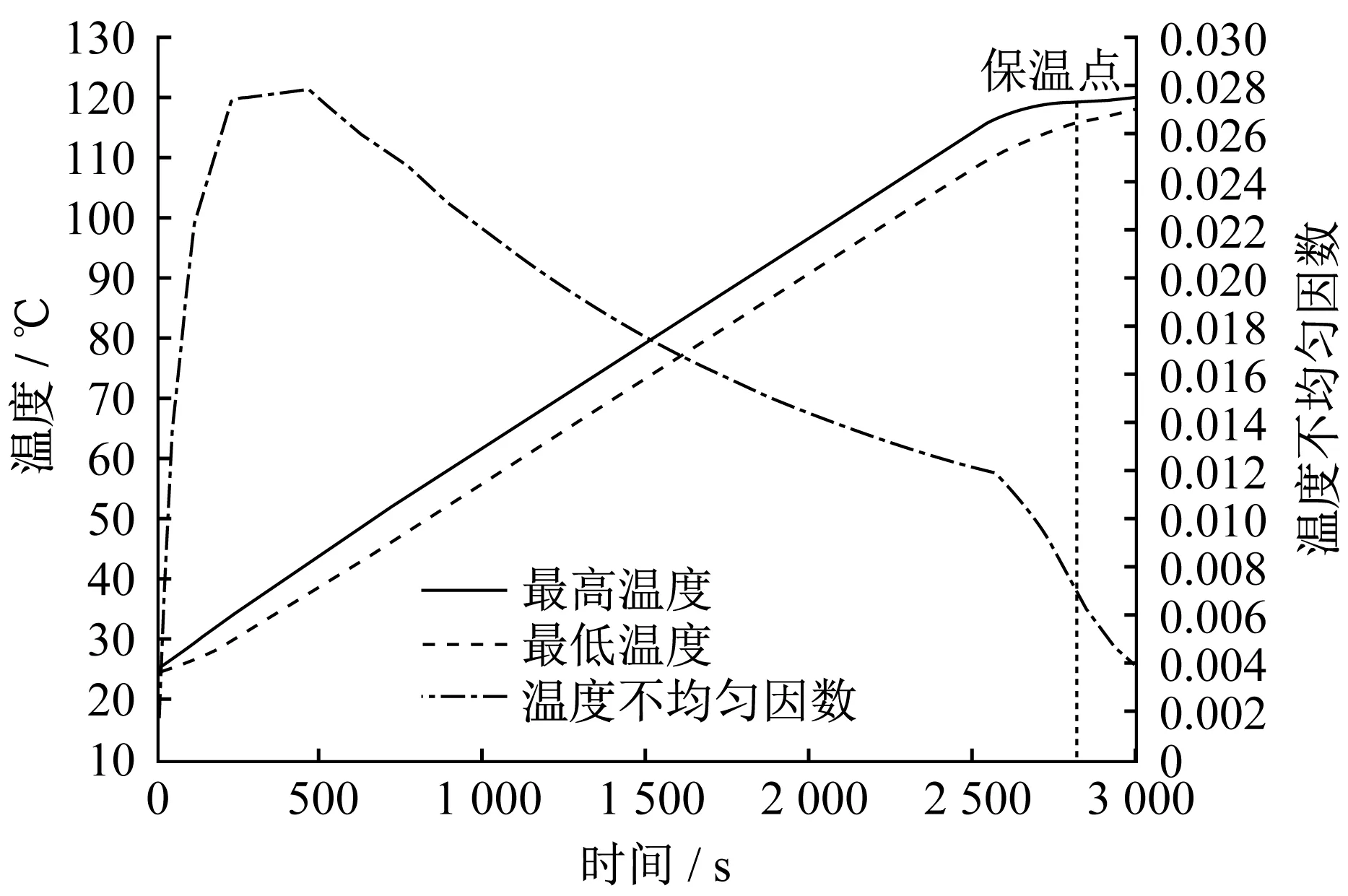
▲圖17 圓形噴涂方案溫度變化曲線

▲圖18 正方形噴涂方案溫度變化曲線

由分析可以發現,仿線圈形狀噴涂方案最優,可以在較短時間內滿足熱板目標面的溫差要求,溫度不均勻因數小于0.001。全噴涂方案整體加熱速率低于仿線圈形狀噴涂方案,但優于其余四種噴涂方案。全噴涂方案在加熱時間達到1 120 s的過程中,溫差較大,接近12 K,在施加保溫電流后,最終溫差與仿線圈形狀噴涂方案幾乎一致,為0.2 K。當然,全噴涂方案經濟成本較高。三角形噴涂方案加熱速率良好,處于六種噴涂方案中間值,但加熱過程中熱板目標面溫差過大,大于50 K,雖然可以采用保溫電流方式來調節最終溫差,但最終溫差仍然接近5 K左右。菱形噴涂方案、圓形噴涂方案、正方形噴涂方案雖然在加熱過程中可以將溫差控制在5～7 K,但是在加熱速率方面遠低于其它三種噴涂方案,并且耗能大。

由加熱過程中熱板目標面溫度不均勻因數的變化趨勢可以看出,未達到目標溫度120 ℃時,六種噴涂方案在加熱初期溫度不均勻因數呈線性增大趨勢,并迅速達到峰值,其中,三角形噴涂方案在加熱420 s后達到峰值0.136,菱形噴涂方案、正方形噴涂方案、圓形噴涂方案在加熱370 s后依次達到峰值0.027、0.027、0.024,仿線圈形狀噴涂方案在加熱130 s后達到峰值0.042,全噴涂方案在加熱100 s后達到峰值0.054。在六種噴涂方案溫度變化曲線中,還有溫度不均勻因數第二次下降的現象,這是因為施加保溫電流后,熱板目標面溫度的均勻性得到迅速改善,三角形噴涂方案由未施加保溫電流時的0.092下降到施加保溫電流后的0.01,菱形噴涂方案、正方形噴涂方案由0.01下降到0.001,圓形噴涂方案由0.008下降到0.004,全噴涂方案、仿線圈形狀噴涂方案分別由0.012、0.12下降到接近于0.000 1。綜合評估六種噴涂方案目標面的溫度不均勻因數,可以得到仿線圈形狀噴涂方案為最優方案。

4 仿線圈形狀噴涂方案參數優化

綜合以上分析,選擇仿線圈形狀噴涂方案進行參數優化設計。通常影響熱板表面溫差的主要因素為加熱頻率、線圈與噴涂層距離、加熱電流。正交試驗能夠從全面試驗中選取具有代表性的試驗組合,使試驗具有均勻分散、齊整可比的特點,在多因素多水平研究中可以大幅減少試驗次數,在各研究領域都得到廣泛應用。筆者選擇加熱頻率、線圈與噴涂層距離、加熱電流三個主要因素,確定三因素三水平正交表,正交試驗因素和水平見表2。

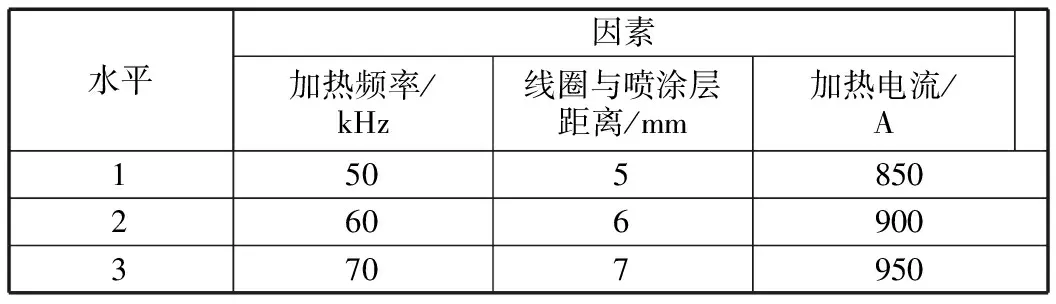
表2 正交試驗因素和水平

根據表2設計正交試驗,由L9(33)正交表得到九種變量組合,應用COMSOL軟件進行三維瞬態求解,試驗結果為仿線圈形狀噴涂方案熱板表面溫差。正交試驗結果見表3。

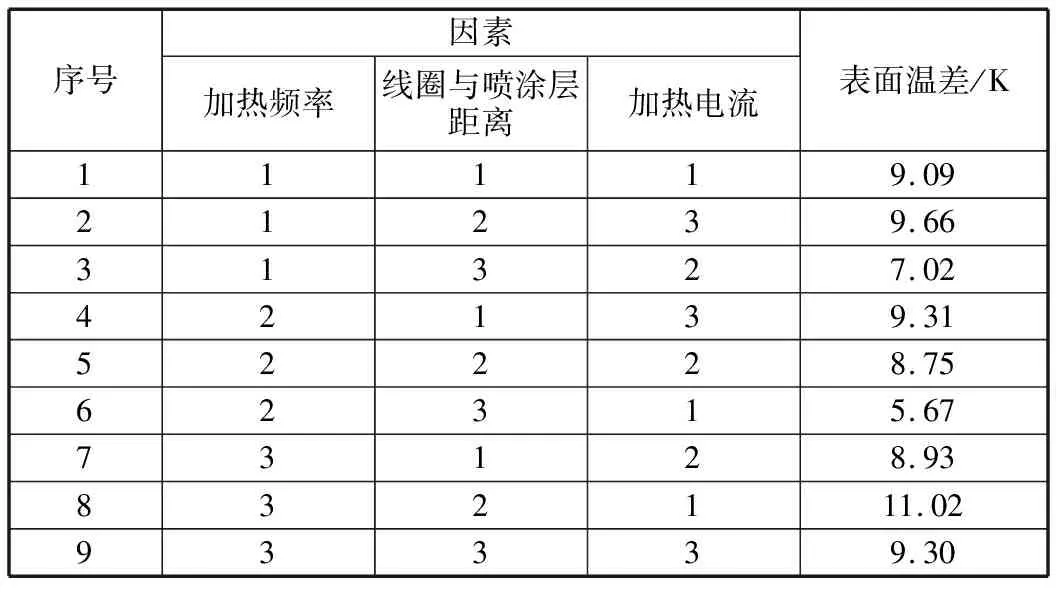
表3 正交試驗結果

利用極差分析法對試驗結果進行分析,見表4。極差R表示任意一列因素水平的試驗指標最大值與最小值之差,Ti表示任意一列中水平i所對應的指標之和。由分析結果可知,仿線圈形狀噴涂方案各因素對溫差影響從大到小為線圈與噴涂層距離、加熱頻率、加熱電流。

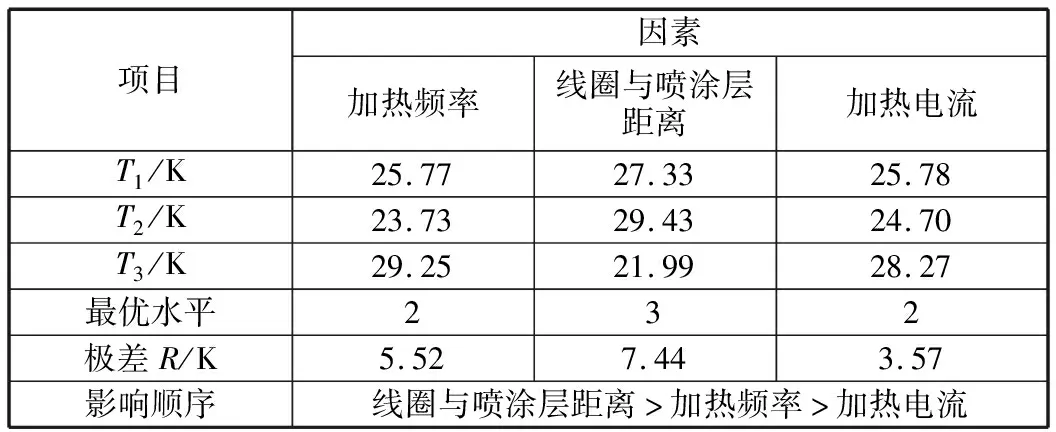
表4 極差分析

根據Ti的大小可以判斷三個因素的最優水平,試驗指標,即熱板表面溫差越小越好,因此應選擇每個因素小指標所對應的水平。由表4可見,各因素的最優水平組合為加熱頻率60 kHz、線圈與噴涂層距離7 mm、加熱電流900 A。

得出最優參數組合后,對仿線圈形狀噴涂方案采用COMSOL軟件進行三維瞬態模擬分析,得出熱板表面溫度分布云圖,如圖19所示。優化前后熱板表面溫度不均勻因數曲線如圖20所示。

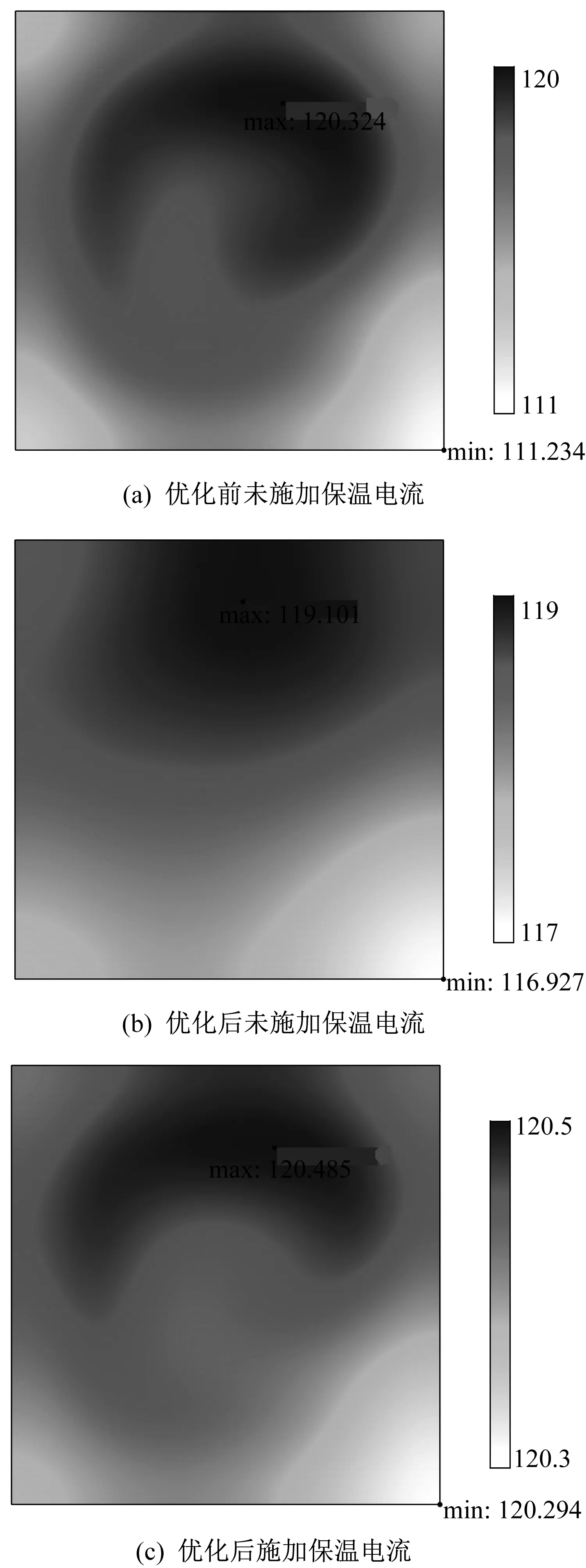
▲圖19 熱板表面溫度分布云圖

經正交試驗極差參數優化后,未施加保溫電流時,熱板表面溫差由為9.1 K減小為2.2 K。施加保溫電流后,保溫時間縮短,溫差進一步減小至0.2 K,優化后的結果符合硫化行業標準。

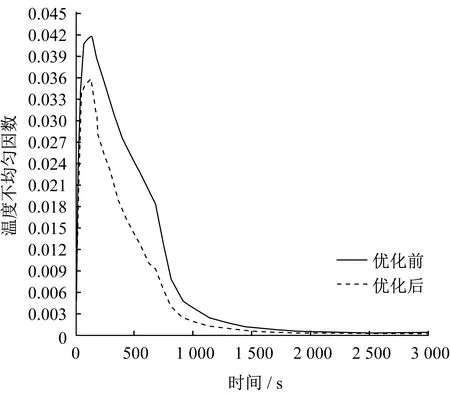
▲圖20 熱板表面溫度不均勻因數曲線

5 結束語

為了研究電磁感應加熱過程中硫化機熱板溫度場,采用COMSOL軟件進行了仿真模擬,分析噴涂不同形狀45號鋼涂層加熱效率與溫差的關系、熱板表面目標溫度及噴涂尺寸與保溫電流的關系、噴涂尺寸與加熱速率的關系,并采用正交試驗對最優方案參數進行優化,以達到減小溫差的目的。

當熱板表面目標溫度從60 ℃提高到200 ℃時,保溫電流從30 A增大到120 A。

通過不同噴涂方案噴涂45號鋼涂層,在頻率為50 kHz,加熱電流為850 A,保溫電流為110 A,線圈與熱板距離為5 mm的條件下,菱形噴涂方案、全噴涂方案、三角形噴涂方案、仿線圈形狀噴涂方案、圓形噴涂方案、正方形噴涂方案六種噴涂方案中,仿線圈形狀噴涂方案加熱效率最高,加熱710 s后,熱板表面溫度可達到120 ℃。

利用正交試驗與極差分析對仿線圈形狀噴涂方案進行參數優化,各因素對溫差的影響程度從大到小為線圈與噴涂層距離、加熱頻率、加熱電流。用最佳參數組合進行模擬,在未施加保溫電流時,溫差由原來的9.1 K減小到2.2 K,在施加保溫電流后,溫差進一步減小至0.2 K。