導引頭伺服系統穩定回路擾動觀測器設計

趙明翰, 鄭秋實, 顧家瑋, 韓道達, 李乃星

(上海無線電設備研究所,上海 201109)

0 引言

導引頭是導彈的重要組成部分,其測量精度將直接影響導彈的性能。隨著軍事現代化的不斷發展,現代化武器對導引頭測量精度提出了更高的要求。傳統的導引頭伺服系統大多采用線性超前滯后的方法來設計控制器,這種方法設計的控制器具有設計簡單、調試方便的優點,但是對系統中的干擾力矩和不確定因素的抑制能力有限。為了進一步提高導引頭伺服系統的精度,需要對設計方法進行優化。

導引頭伺服系統主要有三種工作狀態:預定回路、穩定回路和跟蹤回路,三個回路分別完成不同的任務[1-2]。穩定回路用于保證天線中心軸在慣性空間中的指向穩定。由于導彈彈體在飛行過程中存在擾動,所以需要通過導引頭伺服系統反向偏轉來維持天線中心軸在慣性空間中指向穩定。由于系統中存在較為明顯的摩擦力矩和機構傳動間隙,且不同環境條件下摩擦力矩和機構傳動間隙還存在變化的可能性,傳統的線性超前滯后控制器對于上述非線性環節的抑制效果不盡如人意,需要進一步優化相關設計。文獻[3]采用雙口內模控制的方法提高了去耦性能,并獲得了較好的魯棒性。另外自抗擾控制[4-8]、自適應模糊比例-積分-微分(PID)控制[9]、自適應內模控制[10]、擾動觀測器[11-12]等方法在非線性環節抑制方面的應用,均取得了一定的效果。

這里需要指出的是,導引頭伺服系統的摩擦力矩和機構傳動間隙較易受到環境變化的影響。不同的環境溫度、濕度以及潤滑情況都會對摩擦力矩和機構傳動間隙產生較為明顯的影響,所以常見的靜態補償方法并不能獲得理想的非線性環節抑制效果,需要采用動態補償的方法來優化控制系統性能。

1 系統建模

導引頭穩定回路的主要功能是隔離導彈飛行過程中彈體的擾動,保證天線中心軸在慣性空間中指向穩定。其工作原理如圖1所示。

圖1 穩定回路工作原理框圖

圖1中被控對象由電機和負載組成,其動力學方程為

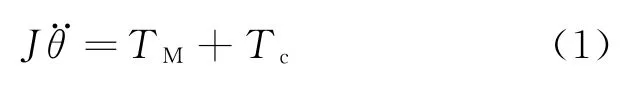
由于系統中的電機選用的是直流電機,根據電磁感應原理和動力學原理,描述直流電機動態特性的時域方程可以表示為

式中:Tem(t)為電磁轉矩;Kt為轉矩系數;Ia(t)為電樞電流;Ea(t)為電樞反電勢;Ke為反電勢系數;ω(t)為電機轉子的角速度;Tc(t)為干擾力矩;Ua(t)為電樞兩端輸入電壓;La為電樞電感;Ra為電樞電阻。

對式(2)進行零初始條件的拉普拉斯變換,可以得到

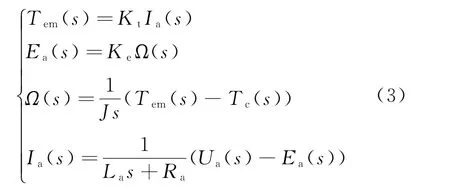
式中:Ω(s)為電機轉子角速度ω(t)的拉普拉斯變換。

由于式(3)中的干擾力矩Tc(s)主要受摩擦、死區、間隙等典型非線性環節影響,因此在處理的過程中,將這部分干擾力矩單獨提出,作為整體傳遞函數中的非線性環節。將剩余的環節線性化后,可以得到以角速度為輸出、電壓為輸入的直流電機傳遞函數

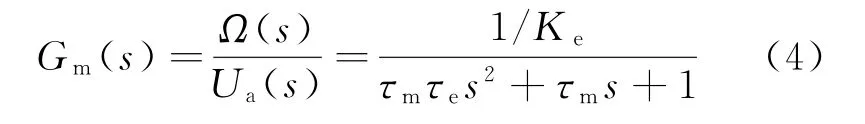
式中:τm,τe分別表示機械時間常數和電磁時間常數。

代入相關參數后得到的直流電機傳遞函數為

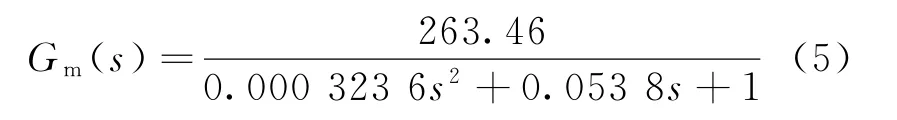
由于被控對象在實際的機械系統中存在摩擦,導致系統存在一個不可忽略的死區非線性環節。角速度傳感器可以近似為一個比例環節,陀螺的傳遞函數為

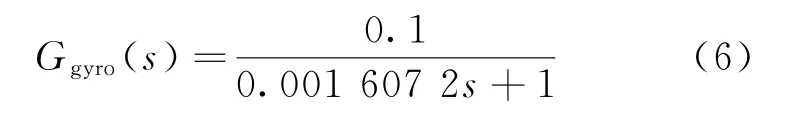
機電伺服系統由于存在機械傳動鏈,不可避免會出現諧振現象。針對機械傳動結構中存在的不易建模部分,對機械傳動系統進行掃頻,將得到的結果進行數據擬合,得到的不易建模的兩個環節的傳遞函數為

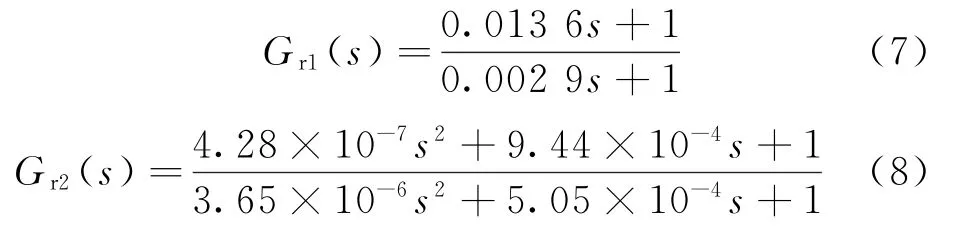
最終得到的被控對象的傳遞函數為

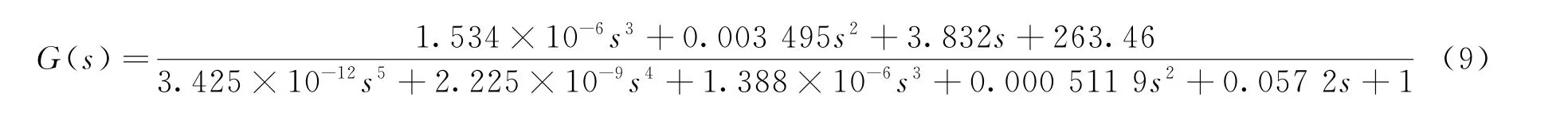
2 擾動觀測器設計

對于系統中存在的摩擦干擾力矩,通常采用基于模型的補償方法。先對摩擦力矩進行建模分析,再對實際系統的參數進行辨識,獲取摩擦力矩模型的具體參數,最后在控制器中對摩擦干擾力矩進行補償。這種方法是一種靜態補償的方法。當系統中的摩擦力矩相對穩定時,靜態補償可以獲得比較好的補償效果。但如果摩擦力矩本身具有一定的不確定性,或者在進行建模辨識的過程中出現了一定的偏差,靜態補償就難以獲得理想的補償效果,需進行動態補償。

動態補償的方法主要有兩種。一種是采用基于狀態反饋的擾動觀測器,通過觀測系統的狀態變量來對系統進行實時補償。這種方法相對復雜,要求相關的狀態變量具有能觀性,且需在設計擾動觀測器的同時完成狀態反饋控制器的設計。另一種是采用基于輸出反饋的擾動觀測器,通過將系統實際輸出與名義輸出進行比較來對系統的摩擦干擾力矩進行實時補償。這種方法結構簡單,不需要知道系統中的狀態變量信息,僅僅依靠系統輸出就可以完成擾動的實時補償[13]。

當導引頭伺服系統摩擦模型相對復雜,相關參數辨識困難,且系統處于不同環境條件時,摩擦參數存在較明顯的差異,基于模型的補償方法無法解決導引頭伺服系統中由于摩擦引入的干擾力矩問題。

將式(9)得到的模型用狀態空間方程[14-15]表示,表達式為

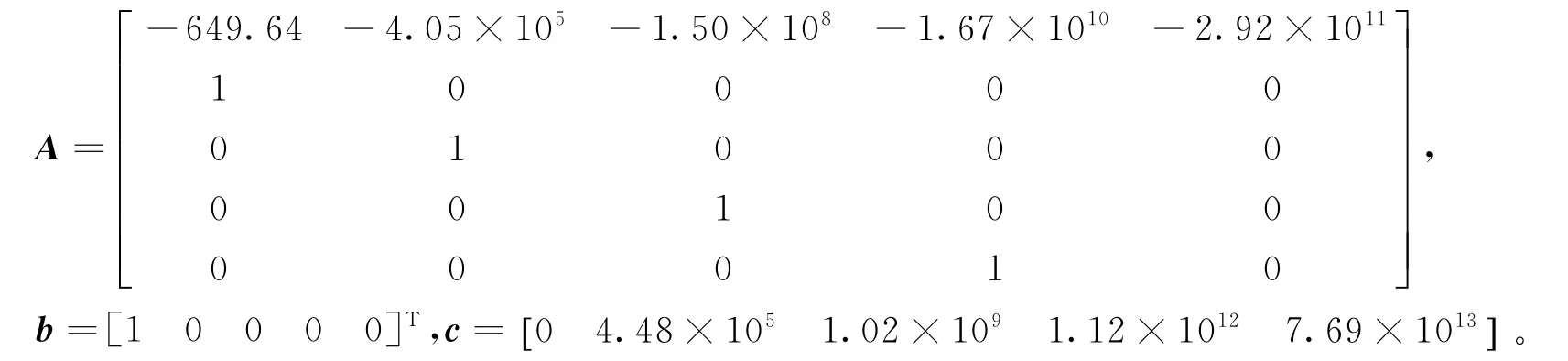
經計算可知,能觀矩陣Qc=[c cA c A2cA3cA4]T的秩為4,按照能觀性判據,系統不完全能觀,所以不能采用狀態觀測的方法來進行擾動的實時補償。故選擇第二種補償方式,利用輸入輸出信息對系統擾動進行實時補償。基于輸出反饋的擾動觀測器框圖如圖2所示。

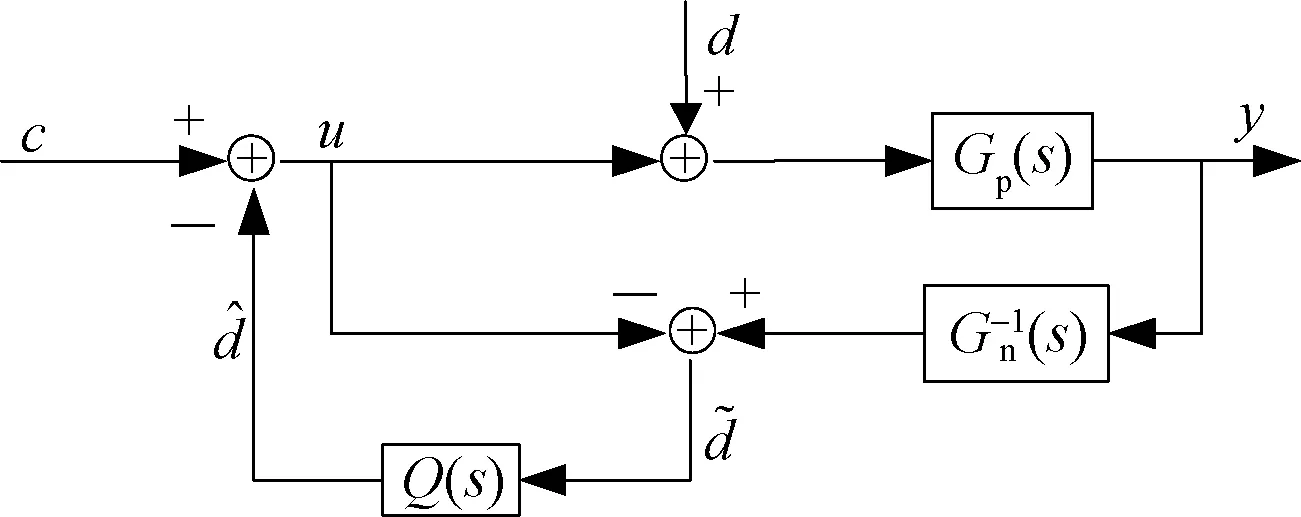
圖2 基于輸出反饋的擾動觀測器

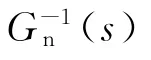
由于在實際工程實踐中,名義對象的傳遞函數求逆通常不能實現,所以將圖2進行適當簡化變形得到圖3。

圖3 簡化變形后的擾動觀測器

在實際系統中,由于傳感器并不理想,導致其輸出中往往會疊加量測噪聲,所以需要分析設計的擾動觀測器對量測噪聲的響應情況。含有量測噪聲的擾動觀測器框圖如圖4所示。

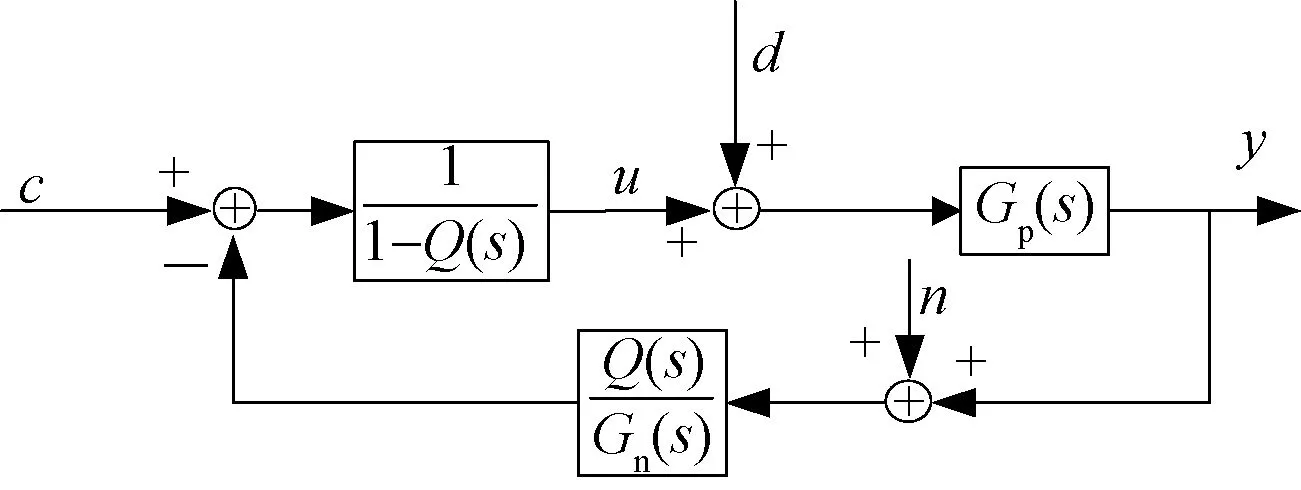
圖4 含噪聲的擾動觀測器

由圖4可知,擾動-輸出的傳遞函數Gdy(s)和噪聲-輸出的傳遞函數Gny(s)分別為

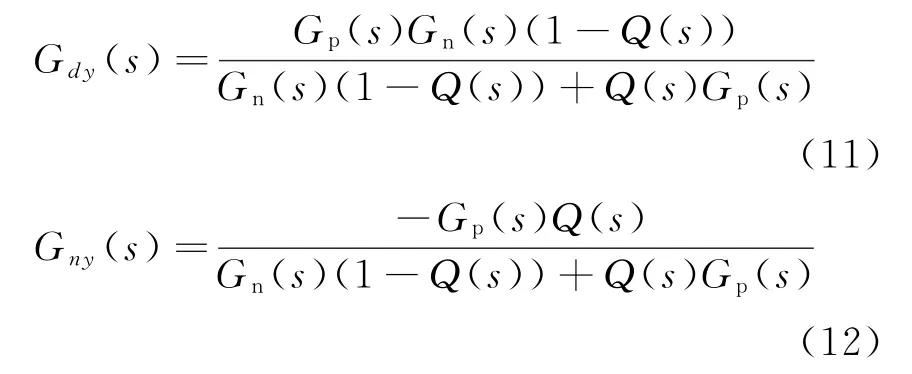
由式(11)和式(12)可知,在低頻段內,Q(s)趨近于1時,能夠抑制擾動信號;在高頻段內,Q(s)趨近于0時,能夠避免傳感器量測噪聲對系統的影響。基于上述原則對Q(s)進行設計,由于被控對象是二階的,則

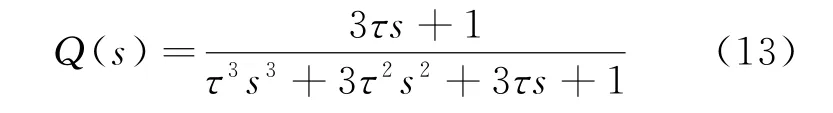
式中:τ為低通濾波器的時間常數。從帶寬和魯棒性兩個角度考慮,最終確定τ=0.006 2。

3 仿真驗證

為了驗證導引頭伺服系統穩定回路中擾動觀測器對非線性環節和噪聲的抑制效果,分別施加兩種正弦信號,驗證系統性能。施加的正弦信號

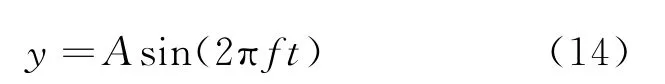
式中:A為正弦信號幅度,取值為0.1 rad/s;f為正弦信號的頻率,取值分別為1 Hz和3 Hz。

對于穩定回路而言,衡量其性能的指標是去耦系數K,計算公式為

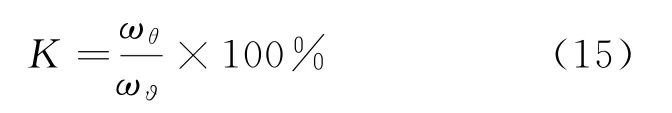
式中:ωθ表示視線角速度輸入為0時,天線中心軸相對慣性空間轉動的角速度;ω?表示彈體相對慣性空間轉動的角速度。

當不考慮系統中的非線性環節及相關擾動時,天線中心軸角速度仿真結果如圖5所示。

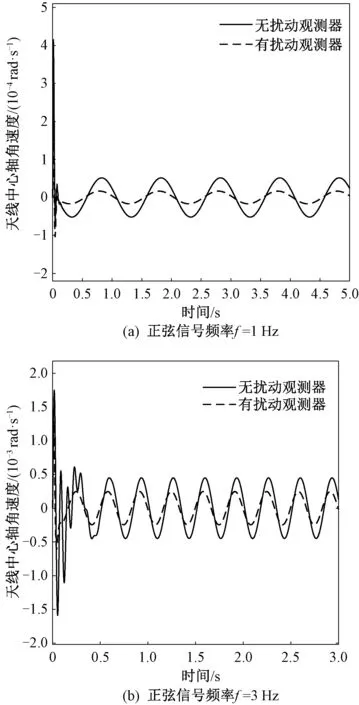
圖5 不考慮系統非線性時天線中心軸角速度

可以看出,當不考慮系統中的非線性環節時,使用擾動觀測器能夠較為明顯地提高系統的去耦能力。對應的指標如表1所示。

表1 不考慮系統非線性情況下的去耦系數

由于摩擦環節的存在,當電機力矩小于最大靜摩擦時,對外輸出力矩為0。只有當電機力矩大于最大靜摩擦時,才能對外輸出力矩。為了簡化仿真過程,將系統中的摩擦環節等效為死區非線性環節。當考慮系統中的非線性環節時,天線中心軸角速度仿真結果如圖6所示。

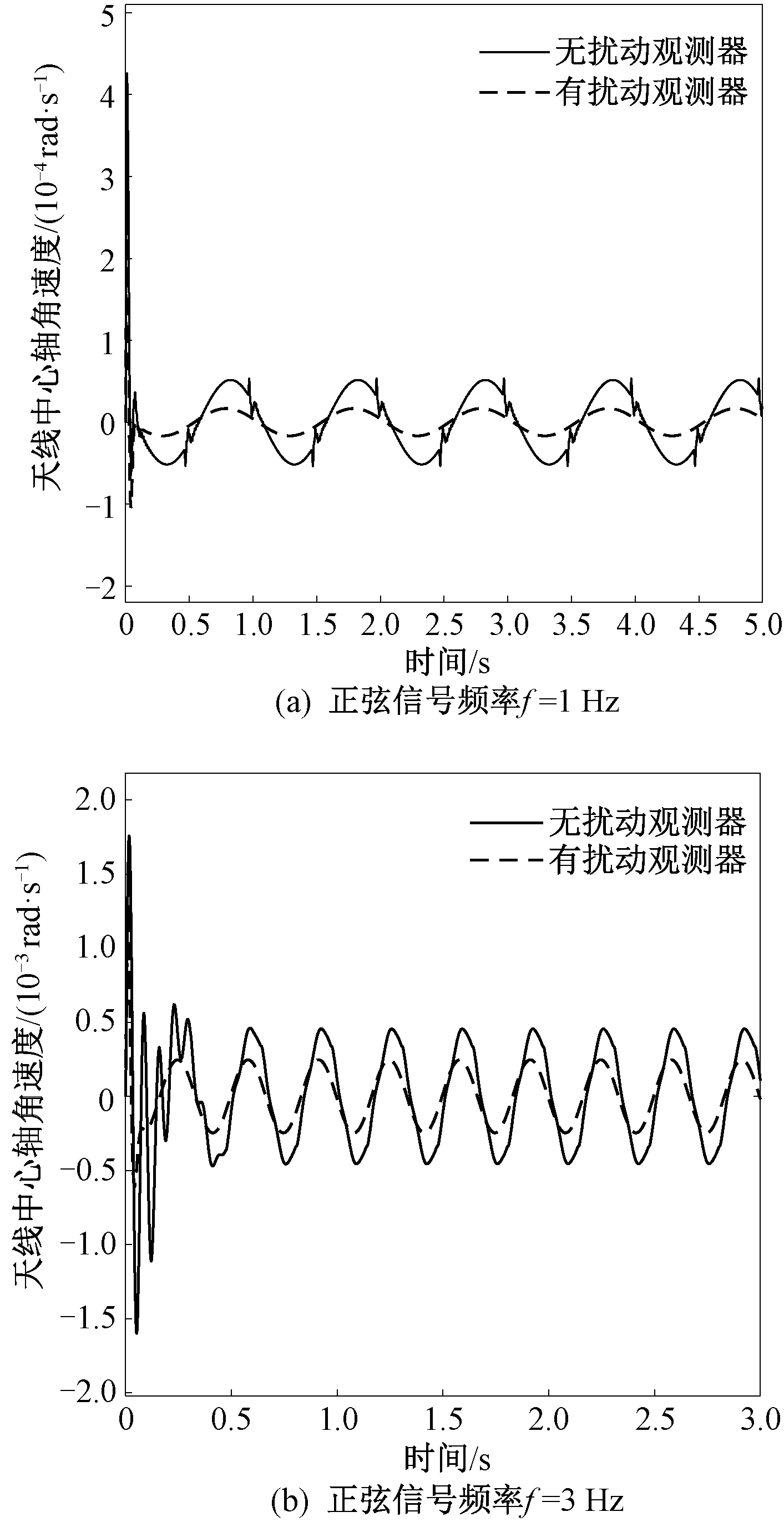
圖6 考慮系統非線性時天線中心軸角速度

可以看出,當考慮系統中存在的非線性環節時,天線中心軸角速度曲線出現了畸變,系統的去耦性能出現了一定程度的下降。具體的指標見表2。

表2 考慮系統非線性情況下的去耦系數

當考慮傳感器噪聲時,天線中心軸角速度仿真結果如圖7所示。其中噪聲為白噪聲,對應的功率譜密度為10-9rad2/s。此時對應的去耦性能指標見表3。可以看出,當系統中存在傳感器噪聲時,穩定回路的去耦性能會受到影響,但影響程度有限。在抑制噪聲方面,盡管擾動觀測器對噪聲的抑制能力有限,但使用擾動觀測器依舊能夠獲得更好的去耦性能。

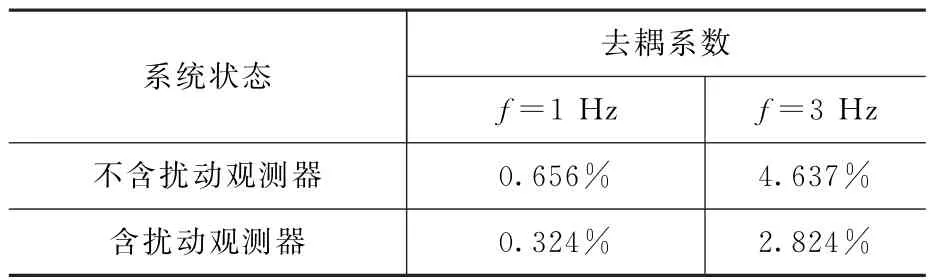
表3 考慮傳感器噪聲時的去耦系數

4 結束語

導引頭伺服系統穩定回路的功能是保持天線中心軸在慣性空間中指向穩定。但是由于導引頭伺服系統固有的工作特點,導致采用基于模型的方法無法對摩擦環節引入的干擾力矩進行補償。采用基于輸出反饋的擾動觀測估計方法對擾動進行動態補償,可以獲取更好的穩定回路去耦效果。同時,通過理論分析與仿真驗證,證明了本文設計的擾動觀測器能夠在存在量測噪聲的情況下獲得較為理想的去耦效果。