一種基于改進遺傳算法的寬帶吸波材料優化設計方法

邢正維,梁迪飛,劉 川,劉 倩,李健驍

(電子科技大學 國家電磁輻射控制材料工程技術研究中心,四川 成都 611731)

隨著雷達探測技術的快速發展,其對己方軍事目標的威脅已經越來越大。先進的吸波材料應滿足厚度薄、重量輕、吸收帶寬寬、吸收能力強的要求[1]。傳統的單一吸波材料因吸收峰單一、吸波頻段窄而難以滿足當前寬帶的吸波性能需求。而多層吸波材料可以將各組分材料的性能互補和關聯,在很大程度上拓寬了吸波帶寬,可獲得單一材料所不能達到的綜合性能[2-3]。目前的研究主要采用多層傳輸線理論或多層均勻平面分層介質理論,結合計算機輔助設計多層吸波材料。采用的優化算法主要有:遺傳算法(GA)[4]、粒子群優化算法(PSO)[5]、差分進化算法(DE)[6]、蝴蝶優化算法(BOA)[7]、人工蜂群算法(ABC)[8-9]等。盡管很多研究人員在多層優化的問題上嘗試了不同的優化算法,但優化中間結果的適應度評估函數還是采用了均值、平方求和、權重系數法等[8-11]。這些設定的適應度函數并不能很好地反映優化的需求,如:權重系數法的權重系數設定就對優化的結果影響很大,而且難以找到一個適用于所有優化目標的權重系數。目前的多層設計研究更趨向于研究算法的尋優能力,而忽略了將吸波優化需求轉化為合理數學模型的重要性。事實上影響吸波優化設計結果的不僅僅是算法的尋優能力,優化需求的數學模型轉化即適應度函數也很重要。

本文的適應度函數依據優化的目標帶寬和最小反射損耗定義,能很好地反映真實的優化需求。針對帶寬和厚度的多目標優化,引入了優化設計總厚度和帶寬均衡的措施,即可以選擇犧牲一些吸波性能來降低優化設計的總體厚度。基于遺傳算法結合上述改進可以很好地優化出符合需求的結果,并通過優化一個帶寬2～18 GHz、最小反射損耗-10 dB 的多層設計實例進行驗證。

1 結構與原理

1.1 多層吸波材料優化設計的結構與理論

多層吸波材料優化設計的結構如圖1 所示,均勻平面波垂直入射到多層吸波材料表面,中間的N層為吸波材料,底層為金屬板。根據電磁波的等效傳輸線理論可等效為圖2 所示的N段不同的均勻傳輸線級聯的電路模型[12]。

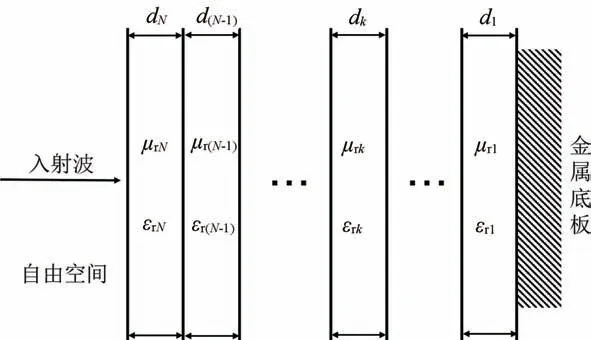
圖1 多層吸波材料結構示意圖Fig.1 Schematic diagram of multilayer absorbing material structure

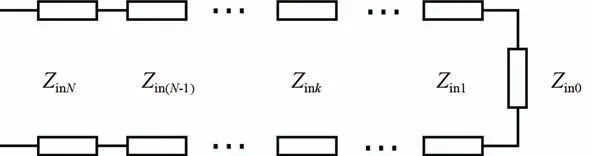
圖2 等效傳輸線電路模型Fig.2 Equivalent transmission line circuit model

依據等效的電路模型最終可以遞推地求解出多層吸波材料的等效輸入阻抗。其中從第k層看進去的等效輸入阻抗采用如下公式計算:

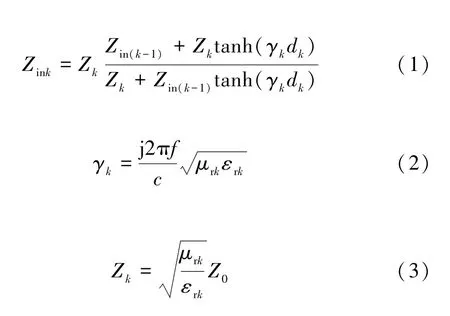
式中:Zink表示第k層吸波材料的等效輸入阻抗;Zin(k-1)表示第(k-1)層材料的等效輸入阻抗;Zk表示第k層材料的波阻抗;dk為第k層材料的厚度;μrk為第k層材料的相對磁導率;εrk為第k層材料的相對介電常數;f為頻率;c為光速;為空氣的波阻抗,μ0和ε0分別為真空的磁導率和介電常數。第0 層的材料為金屬可當作理想導體,因此其特性阻抗為Zin0=0。遞推求解出多層吸波材料的等效輸入阻抗后,可依據下式計算出多層吸波結構的反射率:

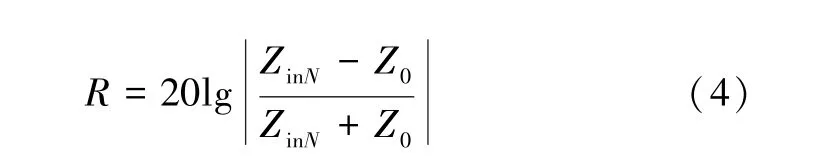
1.2 數據庫材料的吸波特性

吸波材料的吸波性能主要由磁性吸收劑羰基鐵粉、鐵硅鋁等的特性決定。多層吸波材料的吸波性能跟每一層材料的吸波特性相關。因此針對設定的優化目標,需要數據庫的不同材料具有交叉覆蓋全頻段的吸波性能。本次優化使用的數據庫參數包括羰基鐵粉和鐵硅鋁與石蠟不同比例混合制環測得的電磁參數。依據公式(1)簡化的單層反射率計算模型可計算對應的反射率,得到的球形羰基鐵材料厚度為2 mm 具有的吸波性能如圖3 所示。

圖3 羰基鐵吸收劑不同比例反射率Fig.3 Reflectance of different ratios of carbonyl iron absorbent

可見隨著吸收劑比例的提高,反射率的吸收峰向低頻移動,鐵硅鋁也具有此類規律。此外同一種材料比例一致時,隨著厚度的增加,反射率峰值也向低頻移動,如圖4 所示。

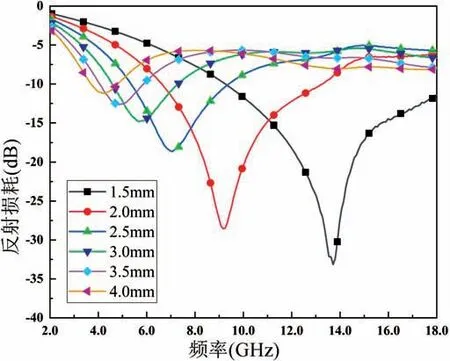
圖4 羰基鐵吸收劑同種比例不同厚度反射率Fig.4 Carbonyl iron absorber with the same proportion and different thickness reflectivity

因此選用不同種類和厚度的材料進行多層設計,理論上是可以拓展吸波帶寬的。此外依據文獻[13]所述,為了實現某一吸波帶寬的某一設定反射損耗,基于材料的性能有一個極限的最小厚度。因此在給定優化目標和數據庫之后,多層優化設計展寬帶寬有一個上限。這個上限由材料庫材料性能、優化目標頻段、總厚度約束、最小反射損耗所共同決定。

2 遺傳算法優化設計

改進后的遺傳算法優化設計流程如圖5 所示,下面給出具體的設計分析。

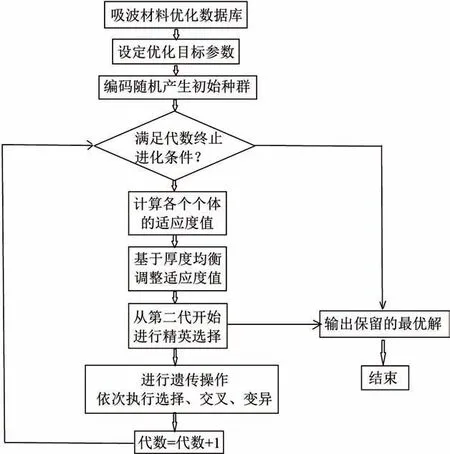
圖5 遺傳算法優化設計流程圖Fig.5 Genetic algorithm optimization design flow chart

2.1 編碼方案設計

采用二進制對多層材料進行種類和厚度的編碼,種群中的每一個個體的染色體編碼形式為S1D1S2D2…SiDi…SnDn。其中Si代表第i層材料的種類編碼,Di表示第i層材料的厚度編碼,兩者組成的二進制串SiDi就是第i層材料的編碼。每個個體二進制編碼的總體長度依據材料庫的材料種類、單層材料設計的精度(單層厚度保留的小數位數)和單層上下限厚度確定,其公式為:

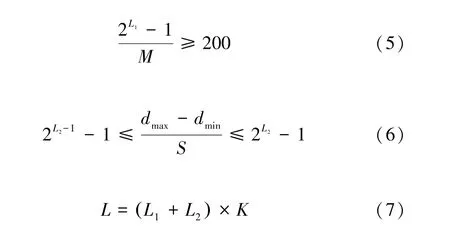
式中:L1表示編碼材料種類需要的二進制位數;M表示數據庫材料種類;L2表示編碼單層厚度需要的二進制位數;dmax與dmin分別代表每層材料厚度的上限與下限值;S表示單層厚度保留的小數位數;K表示優化的總層數;L表示每個個體二進制編碼總長度。

2.2 適應度函數設計

適應度函數是用來評估種群中個體優劣程度的主要指標,因此適應度函數設計的好壞將直接影響到遺傳算法能否找到滿足優化需求的最優解。多層設計的目的是要得到寬帶的吸波優化結果,因此適應度函數必須要能正確的評價個體中寬帶和窄帶吸波的設計結果。為此采用如下的適應度函數:

其中S1和S2如圖6 所示,S2為紅色框選的長方形部分的面積,S1為紅色框選的長方形內部的填充面積,采用微元求和的方法計算,具體計算公式如下:

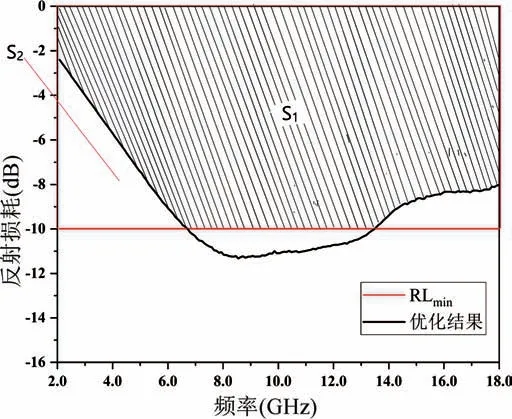
圖6 適應度函數示意圖Fig.6 Schematic diagram of fitness function

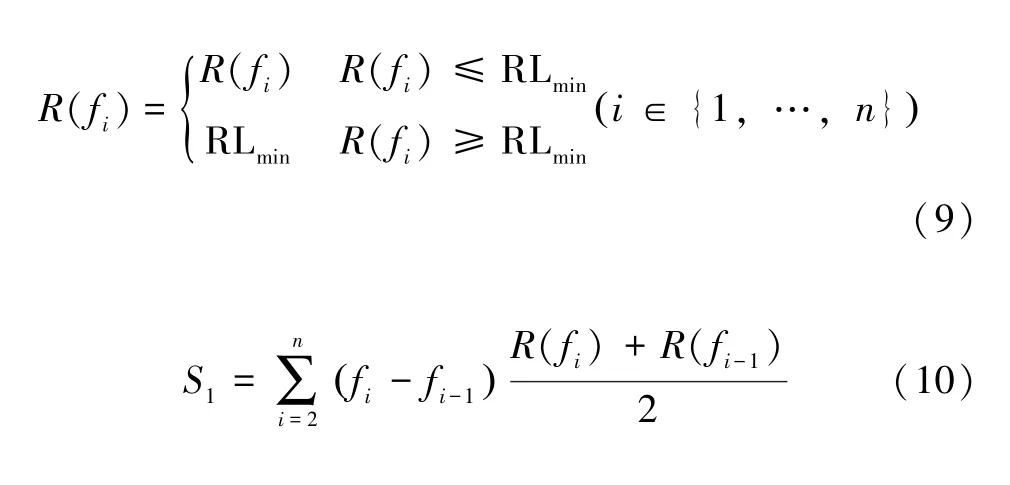
式中:R(fi)表示對應頻點fi處的反射率值;RLmin表示優化設定的最小反射損耗。適應度值反映了紅色框選部分的填充比例,其值域為[0,1]。

2.3 算法的優化改進

多層吸波材料優化設計不僅要求優化的結果盡可能地滿足優化目標,同時也希望優化結果在不超過總厚度約束的情況下盡可能薄。但吸波材料的“薄” 和“寬” 是兩個沖突的要求,為此引入了設計總厚度和帶寬的均衡措施,能對適應度值進行修正。即在優化開始前可以設定厚度約束參數(0 或1),來選擇本次優化是否需要犧牲一些吸波性能降低總體厚度。修正的具體步驟如下:(1)找到種群中適應度值最大的個體,將其適應度值和總厚度作為標準;(2)對小于最大適應度值某一范圍的個體,計算其與最大適應度個體厚度和適應度的差值,然后分別歸一化;(3)將總厚度和適應度的歸一化差值相減,然后加在各自的適應度值上。

為了避免適應度值最大個體在遺傳進化的過程中,被交叉和變異運算破壞,采用了精英選擇策略。將歷代適應度值最大的個體進行復制保留,待到交叉變異結束,用復制保留的個體替換掉種群中最差的個體,然后進行下一代遺傳操作。此外遺傳算法具有容易陷入“早熟” 的缺陷,為此引入了種群多樣性評估,包括個體外部多樣性評估和種群整體多樣性評估,分別用來評估種群個體間的差異程度和種群整體的多樣性程度[14]。個體外部多樣性的計算公式如下:

種群整體多樣性的計算公式如下:

式中:pij表示種群中個體i的第j位二進制值;NP 表示種群大小;L表示每個個體二進制編碼總長度。

2.4 選擇、交叉、變異的設計

遺傳算法的進化過程中,對種群個體的選擇采用無放回余數隨機選擇,而沒有完全采用基于適應度值的概率選擇。保證了適應度值高的個體能夠被遺傳到下一代,降低了選擇誤差[15]。無放回余數隨機選擇的過程如下:

(1)計算種群中各個個體在下一代種群中的期望值:

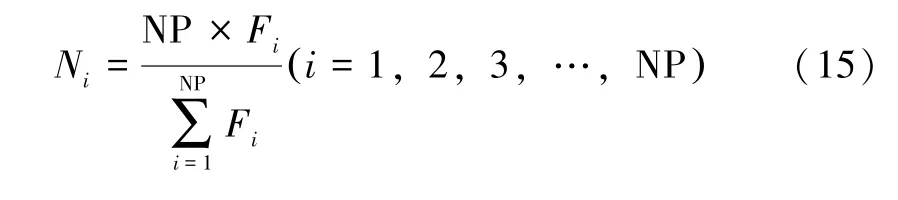
(2)用Ni的整數部分去確定各個對應個體在下一代種群中的數目,由該步共可以確定出下代種群的個個體。

(3) 調整個體的適應度值為:Fi -[Ni]×,種群中的剩余個體采用基于適應度值的概率選擇(輪盤賭策略)來隨機確定。

交叉采用隨機配對的均勻交叉,先對種群中的個體進行隨機選擇兩兩配對,然后兩兩進行基于交叉概率的交叉。變異則采用基于變異概率的基本位變異。

3 結果與討論

基于上述優化設計流程進行優化設計,各遺傳參數的設置如下:

材料庫材料種類:T=18,種群大小:NP=500,迭代次數:G=200,交叉概率:Pc=0.8,變異概率:Pm=0.01。

設定的優化目標參數:優化頻段:2～18 GHz,最小反射損耗:RLmin=-10 dB,單層設計厚度保留小數位數:S=2,設計總厚度約束:2 mm,然后設置不同的層數限制進行優化。不同層數未施加厚度約束和施加厚度約束的優化設計結果如表1。

由表1 可見在無厚度均衡2 mm 總厚度約束下,優化結果適應度最大值為20 層的0.967,其總厚度為1.980 mm。

表1 不同層數有(無)厚度均衡的優化結果Tab.1 Optimization results of different layers with(without) thickness balance

將有(無)厚度均衡的優化數據作圖,由圖7 可見無厚度均衡優化結果在層數較少和較多時,適應度值和總厚度的曲線增減趨勢并不同步,在厚度增加或者下降較大時,適應度值并未有相應比例的增加或者下降。而在20 層左右的中間段,適應度值和總厚度的曲線增減趨勢符合較好,因此該區間段的優化結果更接近于對應材料庫性能、所設優化參數能優化出的結果極限。

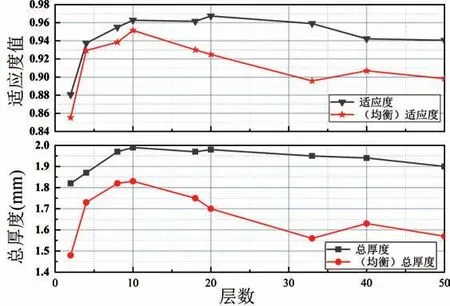
圖7 有(無)厚度均衡優化結果對比Fig.7 Comparison of optimization results with(without) thickness balance

有的時候為了盡可能減少設計的總厚度,可以適當犧牲一些目標頻段的吸波性能。為此引入了厚度均衡措施,圖7 也給出了2 mm 總厚度約束下有均衡措施和無均衡措施優化結果的適應度值、總厚度對比,均衡措施調整適應度值的范圍是種群中適應度值前10%的個體。由優化結果可見取得了一定的效果,能在適應度值減小比例不大的情況下,讓總厚度得到降低。如:33 層的優化結果總厚度下降了約0.4 mm,而適應度值(填充度)僅下降約0.06。此外不同層數優化結果用到的材料種類變化如圖8,可見隨著吸波優化設定層數的增加,吸波優化結果用到的材料種類也會有一定的增多。

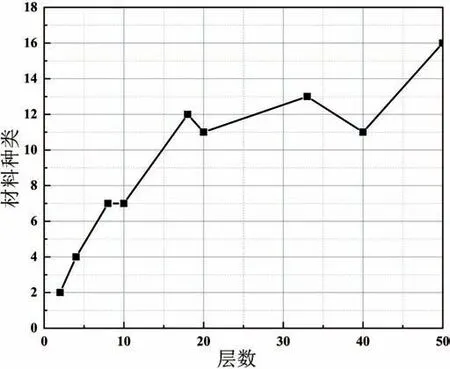
圖8 無厚度均衡優化使用材料種類Fig.8 Optimal use of materials without thickness balance

圖9 給出了20 層有(無)厚度均衡措施的優化結果反射率對比,兩者的適應度值分別為0.967 和0.925。可見加入厚度均衡措施后的優化結果在適應度值上有所下降,減小的主要是低頻部分。所以可以預見在要求厚度較薄的情況下,多層吸波材料優化設計也難以實現低頻部分的吸波性能優化。

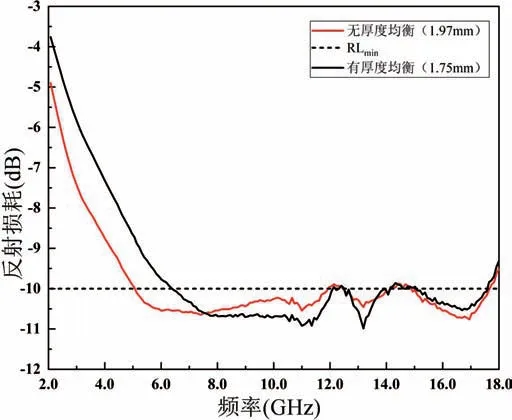
圖9 20 層有(無)厚度均衡優化結果反射損耗Fig.9 20 layers with (without) thickness balance optimization result reflection loss

20 層無均衡措施的優化過程中種群整體多樣性和個體外部多樣性的變化分別如圖10 所示。可見兩者在整體上均呈現為下降趨勢,且個體多樣性還伴隨有波動,這主要是種群的交叉和變異所引起的個體多樣性變化。而種群的整體多樣性僅受變異的影響,因此波動很小。說明交叉和變異有利于防止過早收斂,在一定程度上保證了種群中個體間的多樣性。

圖10 (a)個體多樣性變化;(b)整體多樣性變化Fig.10 (a) Individual diversity changes;(b) Overall diversity changes

另比較了在相同厚度(1.99 mm)下多層優化結果和優化中用到單一材料的反射率。此處選擇10 層的優化結果進行對比,其多層優化結果用到的材料種類為7 種。對比結果如圖11(圖中#數字表示優化數據庫中材料對應的編號),可見多層優化結果的-10 dB 吸波帶寬優于任一單一組分材料。因此多層設計有利于拓展吸波帶寬,但同時也可以看到其沒有了單一組分材料的吸收峰。所以多層設計為了拓展吸波帶寬也會犧牲部分頻段的一些吸波性能。

圖11 10 層優化結果與單一材料反射損耗對比Fig.11 Comparison of 10-layer optimization results and single material reflection loss

4 結論

本文基于改進的遺傳算法進行多層吸波材料的優化設計,用優化區間的填充量定義適應度函數,最終優化得到了符合目標需求的優化結果。并通過對優化結果的分析得到了以下結論:(1)針對某一優化目標,多層吸波設計的層數并不是越多越好,最佳的層數取決于材料庫的材料性能和優化的目標;(2)好的多層吸波設計對比同厚度單一材料,能有效拓展吸波帶寬;(3)在相同厚度下對比多層和其單一組分的吸波性能可以發現,盡管多層設計拓展了吸波帶寬,但也犧牲了部分頻段的吸波性能;(4)在要求厚度較薄的情況下,多層優化設計也難以實現寬帶的低頻吸波效果。