電-熱-固耦合作用下IGBT 高周疲勞壽命評估方法研究

張 陽,王維民,張 楊

(北京化工大學 機電工程學院,北京 100029)

IGBT 器件作為軌道交通車輛牽引變流器和各種輔助變流器的主流電力電子器件,在牽引變流器及其他電動設備于短時間內將時速從零提升到上百公里的過程中,用來實現變壓變頻控制,這種工作特點決定了其在變流裝置中存在較高的失效率,文獻[1-2]給出電力電子變流裝置中各部分的失效率,均指出功率器件及其驅動電路故障導致變流裝置故障所占的比重最大,因此研究IGBT 器件的可靠性在一定程度上有助于提高整個裝置的可靠性。

目前普遍認為IGBT 主要存在兩種疲勞模式:一是導致熱機械應力失效的高周隨機振動疲勞,波動周期通常為幾十秒到幾百秒;二是開關導致的周期結溫波動產生的低周熱應力疲勞,通常波動周期為幾十毫秒到幾百毫秒。兩者作用將導致器件內部及封裝外殼的變形和疲勞損傷累積。由于功率器件在實際工作中不斷經歷功率循環(PC)和溫度循環(TC),且由于模塊各層材料的熱膨脹系數不同,器件內部層級交界處在溫度作用下,產生隨溫度變化的大小不同的熱應力,熱應力的反復作用將加快焊料層、鍵合線、芯片、鍵合線焊點等部位出現不同程度老化,最終導致整個器件失效。研究人員認為應用于鐵路牽引系統中的IGBT模塊的使用壽命應該至少為30 年,失效率不能超過100 FIT(1 FIT=109h-1)[3]。

目前大量研究普遍基于熱應力載荷開展IGBT 模塊可靠性和壽命評估。文獻[4]以基板厚度、焊料層厚度為變量,對模塊進行隨機振動,探究了結構尺寸因素對焊層壽命的影響程度,但未考慮溫度因素在其中的耦合機理及對振動疲勞壽命的影響程度。文獻[5]利用有限元軟件對車載工況條件下的電路板進行模態分析和隨機振動分析,比較了常溫和受熱兩種分析結果。文獻[6]建立了多時間尺度IGBT 三維渦流場計算的有限元-分布參數耦合模型和計算方法,但未進行模塊在長期運行工況下由于熱分布不均而產生的熱-力耦合的研究與分析。文獻[7]綜合考慮風速、環境溫度以及功率器件的時間常數特性,對可靠性評估的時間尺度進行劃分,獲得疲勞損傷、風速波動以及環境溫度波動等對風電變流器IGBT 壽命的消耗。文獻[8]重點研究了IGBT 模塊電熱力多物理場耦合模型的建立及其失效形式和失效機理,未進一步分析模塊在熱載荷和機械載荷共同作用下的可靠性。文獻[9]推導出功率譜密度下結構振動疲勞壽命的一般表達式,分析了結構振動疲勞破壞與模態振型的關系。而功率器件的可靠性受環境溫度、電流強度、機械特性等多因素影響與制約,且因素間相互作用的機理不易分析[10]。現實工況下,熱載荷與振動載荷是影響模塊疲勞壽命的主要因素,考慮振動載荷導致的高周疲勞時,應該考慮熱載荷可能導致的部件應力幅值上升,同時動應力引起的模型變形甚至失效將影響電場和溫度場分布,從而需考慮動應力和熱應力耦合效應下的疲勞壽命。但總體來說,國內外對考慮耦合應力作用下的模塊退化失效研究依然較少,僅有的試驗研究多數也是在單一載荷順序下依次進行的,對于兩種及以上載荷同時作用下的模塊可靠性研究十分有限。

針對現有的對IGBT 電-熱-機械多場耦合壽命評估方法的不足,本文開展了考慮熱載荷影響條件下的振動載荷高周疲勞壽命計算方法研究,綜合考慮熱應力作用對振動疲勞壽命結果的影響,建立了振動載荷下的高周疲勞壽命有限元評估模型。

1 結構振動疲勞壽命計算方法

振動環境下的疲勞分析方法主要是時域法和頻域法。頻域法一般是借助有限元軟件進行動力學計算分析,獲得結構損傷處的應力或應變的功率譜密度函數(PSD),并根據統計理論計算PSD 相關參數,按照一定的損傷累積準則進行疲勞的壽命分析和估算。而時域法需要循環計數,在此基礎上進行數據統計處理后,再進行疲勞壽命分析。對比兩種方法,頻域法更加簡單便捷,適合在工程設計上應用。

假設實測應力-時間歷程為真實隨機過程的一個典型樣本,記G(f)的N階慣性矩函數mn為:

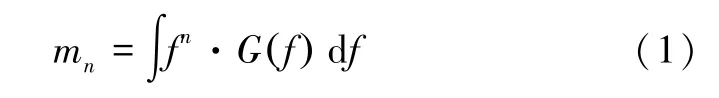
式中:G(f)為頻率f處的單邊PSD。

又材料的S-N曲線表達式為:

式中:b、c為材料常數;N是應力幅值為S時對應的疲勞壽命。

基于功率譜密度的隨機振動疲勞壽命公式[12]可表達為:

式中:m0、m2分別為第0、第2 階慣性矩;smax為實際振動中結構的最大響應應力;sf為結構材料疲勞極限。該壽命計算值單位為秒。

式(3)適用于一般情況下的隨機振動疲勞壽命計算,但求解較復雜,適用于分析軟件計算。工程上可利用高斯三區間法對其進行簡化,并按±3σ對隨機信號進行削波處理,基于Miner 線性疲勞損傷累積準則,提出單位時間內各級應力幅值造成的總損傷DRV為:

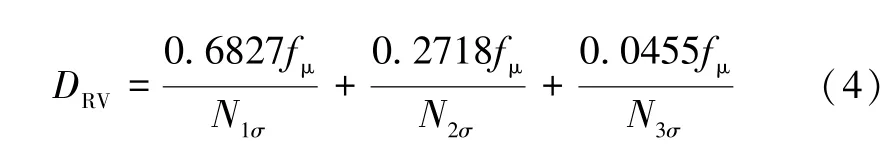
壽命值為損傷的倒數,則結構疲勞壽命可表示為:

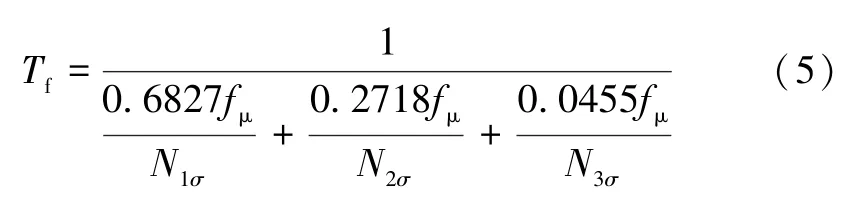
將式(1)、式(3)代入式(5)可得疲勞壽命表達式為:

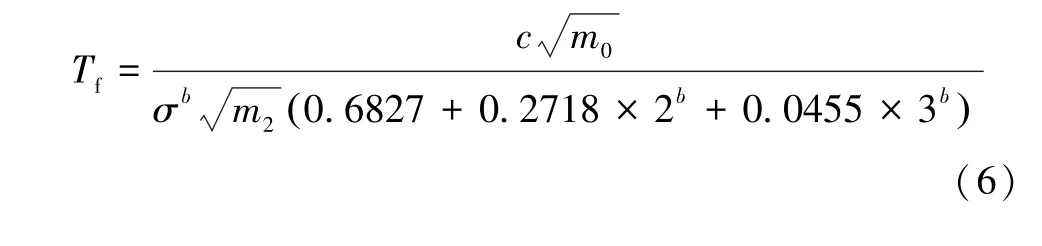
Miner 理論認為每個循環載荷變化都會對器件造成一定的損傷,沒有考慮不同載荷水平順序對壽命的影響,因此可以根據材料在多種工況下的載荷譜并結合Miner 累積損傷理論來預測其疲勞壽命。

熱循環載荷是隨時間變化的時域載荷,而振動載荷具有高頻特性,在有限元數值模擬中,可以在頻域內對熱循環進行處理,得到與隨機振動載荷共同作用下結構的響應。nCode Designlife 預測隨機振動疲勞壽命計數方法采用的是Miner 法則進行累積損傷。溫度循環與隨機振動綜合作用下的總損傷率可表示為:

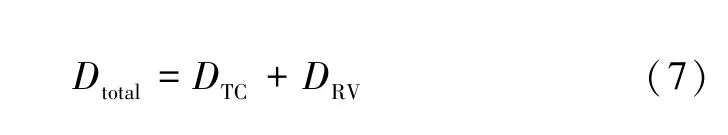
式中:DTC表示溫度循環造成的疲勞累積損傷值;DRV表示隨機振動造成的疲勞累積損傷值。

在一定的激勵頻率下,熱膨脹應力與外部激勵共同作用下引起的振動比單純由溫度梯度產生的熱應力大很多[11]。計算溫度作用下的振動疲勞損傷,即可得到熱與振動共同作用下器件的疲勞壽命。

2 有限元計算仿真

2.1 IGBT 模塊有限元建模

典型的IGBT 功率模塊的內部結構是由多層不同的材料組成,圖1(a)為模塊實體內部結構圖,圖1(b)為其內部剖面及傳熱示意圖。

圖1 IGBT 模塊內部結構Fig.1 Internal structure of IGBT module

建立功率模塊結構的簡化模型,參照文獻[12]簡化研究對象:由于模塊中多部分組件呈循環對稱分布,添加對稱區域設置,只取其中一塊進行分析,將各部分組件都簡化為層狀結構;將鍵合線的橫截面簡化為正方形,上銅層不規則的電路結構簡化為三塊規則的長方體;忽略了下橋臂的IGBT 芯片、二極管芯片、鍵合線,忽略了上橋臂二極管芯片上的鍵合線;由于模塊在運行時整體處于完全封閉狀態,僅通過底面來進行對流換熱,若考慮建立通風或水冷散熱的散熱器模型,將產生電、熱、結構、流場的復雜多物理場耦合情況,且散熱結構復雜,會大大增加有限元網格劃分及計算量,甚至可能導致計算不收斂或誤差較大。因此省略散熱器及外部的塑封外殼建模,其作用效果可通過設置銅基板底面水冷散熱系數來產生等效作用。簡化模型及網格劃分如圖2 所示,IGBT 芯片分別用1,2,3 標出。對模型各層材料賦予材料屬性,表1列出了電-熱-機械有限元分析中使用的材料參數。設置各部件間綁定接觸。對鍵合線、焊料層、芯片采用精細網格剖分,對銅層、陶瓷層尺寸相對較大的部件采用標準網格劃分。

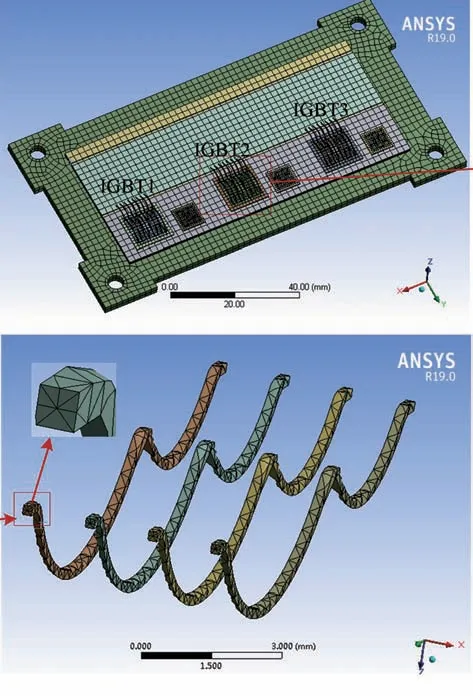
圖2 IGBT 有限元模型Fig.2 IGBT finite element model

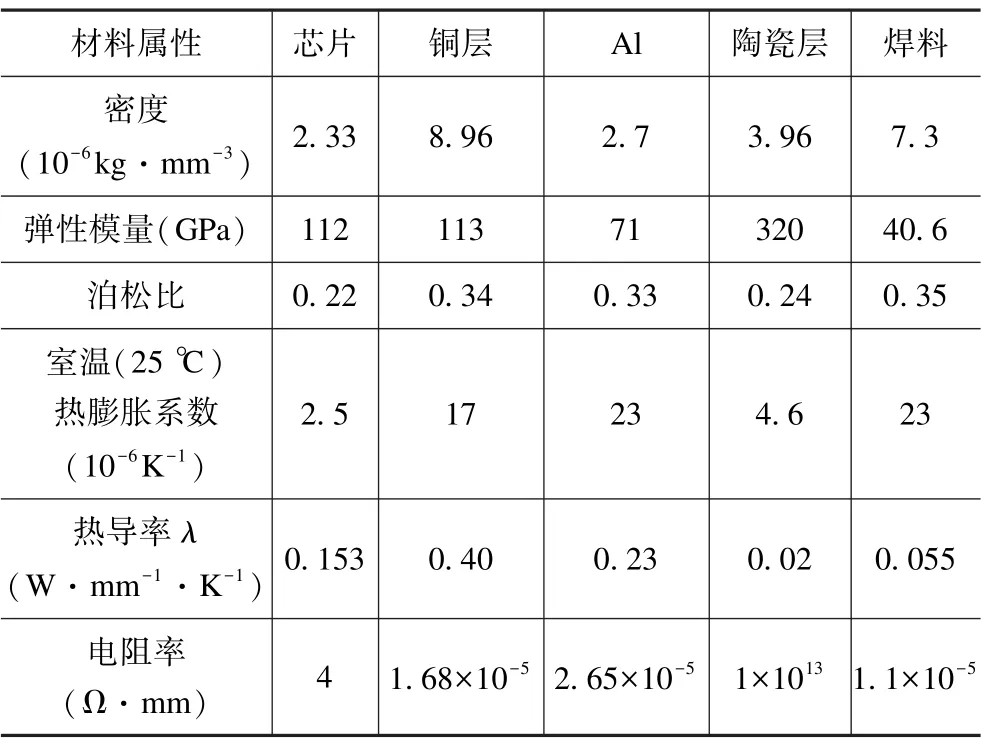
表1 材料屬性Tab.1 The material properties

2.2 IGBT 電-熱-固多場耦合分析

對模塊進行電-熱-機械多場耦合分析,在電與熱作用下產生熱應力的基礎上進行結構分析。首先在IGBT 芯片上施加熱生成率來表征恒導通條件下IGBT芯片的熱源效應,設置熱生成率為3.75 W·mm-3,該值可根據模塊的輸出特性計算得到;設置導通電流在集電極注入,發射極接地。銅基板下表面設定為對流傳熱邊界(第三類邊界)來模擬散熱器的水冷散熱作用,對流換熱系數為0.008 W·mm-2·K-1,環境溫度為22 ℃;基板側面設置為空氣自然對流換熱,系數為2×10-5W·mm-2·K-1,這里為方便計算,取了工程上的經驗系數。基板底面四個圓孔位置設置為固定位移,防止模塊移動,同時基板四周設置為z方向約束,即uz=0[13]。在對稱面上設置對稱性邊界條件,初始溫度取室溫22 ℃。

計算出的模塊溫度場分布云圖如圖3(a)所示,可以看出,IGBT 芯片的中心位置溫度最高,且由于右上端IGBT 芯片最靠近電流流入端,故此芯片上的溫度最高,為94 ℃,低于芯片可承受的工作結溫上限。對于鍵合線,最高溫度位于鍵合處,為86 ℃。由于硅材料的電阻率遠高于鋁材料,IGBT 芯片的產熱量大于Al 鍵合線的產熱量,同時芯片上電流密度及熱流密度均最大,故使得芯片結溫高于Al 鍵合線的溫度。在銅底板與散熱片的接觸面上,銅底板上最高溫度為40 ℃,位于芯片垂直向下映射范圍內。硅芯片與鋁之間因循環加熱冷卻及熱膨脹系數差異,將產生差異性的壓縮及拉伸應力而使鍵合處產生裂紋,進而發生脫落或斷裂。

在結構場分析中導入溫度載荷進行分析,得到熱應力場分布如圖3(b)所示。觀察靜力場應力結果可以發現,模塊熱應力最大值集中在焊料層上表面及IGBT 芯片中心位置,最大值為122 MPa。說明在溫度作用下,鋁金屬化層和IGBT 芯片結合處承受較大的界面熱應力,長期作用容易較早產生裂紋,進而可能會向焊料層中心區域發生損傷擴展。分析原因是焊料層在溫度變化下產生了剪切應力,將導致焊料層結構變形而失效。鋁鍵合引線脫落通常發生在焊料層疲勞失效之前[14]。

模塊熱流率分布如圖3(c),最大值為3.9 W·mm-2,位于IGBT 芯片焊層與上銅層交界線;最大剪切應力值為92 MPa,位于鍵合線和IGBT 芯片鍵合處的邊角處,如圖3(d)所示,在剪切應力的作用下鍵合線易脫落,這也是鍵合線故障的主要形式。同時比較可得,模型中各材料等效熱應力值均低于材料的最大屈服強度。綜上分析,判斷IGBT 模塊最易發生疲勞破壞的模式為芯片熱源產生的熱應力導致鍵合線脫落的電氣失效以及焊料層的焊點由于出現裂紋、空洞等的機械應力失效。

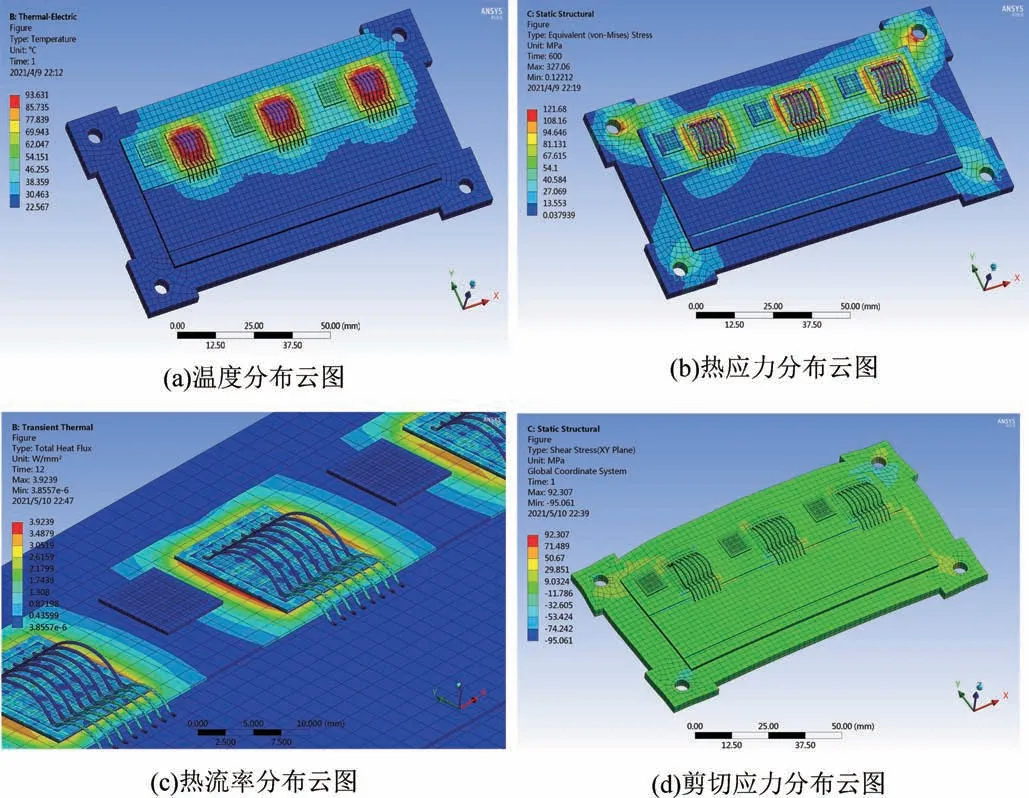
圖3 模塊整體仿真結果Fig.3 Overall simulation results of the module

2.3 模態分析

分析完溫度場和應力場后,將載入溫度載荷的結構分析結果作為預應力傳遞到模態分析,來比較常溫和受熱兩種條件下的前6 階模態分析結果,各階固有頻率值有所降低,但幅度不大。常溫下的模態分析一階固有頻率為982 Hz,受熱時的模塊的一階固有頻率為944 Hz。如圖4 所示,對比兩者變化,前5 階頻率變化率均在6%以內,第6 階頻率變化率在11%左右。分析原因是溫度場使得模塊產生熱變形及熱應力,其中熱應力作為預應力導致模塊各層材料的剛度增大,使得固有頻率增大;且材料楊氏模量也隨著溫度發生變化,影響了模塊振動模態參數。而溫度場引入的熱變形膨脹,降低了模塊的剛度。相對熱應力而言,溫度對模塊固有頻率影響更加明顯。兩者的各階振型基本相同。

圖4 溫度對固有頻率影響對比Fig.4 Comparison of the temperature on natural frequency

模塊在兩種工況下的靜力場求解變形位移如圖5所示,可以看出,模塊在受熱后的一階固有頻率下的變形量減小,其他各階變形量基本一致。變形減小原因是結構剛度提高,使得整體強度上升[5]。使用過程中應盡量避免模塊在一階固有頻率作用下工作。

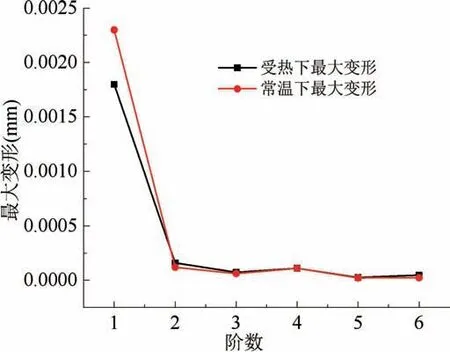
圖5 受熱對最大變形影響對比Fig.5 Comparison of the effect of heat on maximum deformation

前6 階振型如圖6 所示,各階振型直接反映了振動中模塊各部分之間的相對位置變化,可用來分析結構在隨機振動加載下的受力情況和疲勞特性。

圖6 1～6 階模態振型Fig.6 Modules 1-6 mode shapes

3 疲勞壽命分析

3.1 nCode 疲勞分析流程

隨機振動分析是計算結構在隨機載荷作用下的響應,是結構的動態特性,即頻率響應函數和加載到結構上的PSD 共同作用的結果。本文研究的IGBT的疲勞屬于機械低應力高周隨機振動疲勞,以振動試驗標準和理論為基礎,利用nCode Designlife 軟件建立振動疲勞分析模板,輸入由模態疊加法計算出的諧響應分析獲得的頻率響應函數(Frequency Response Function,FRF)的rst 文件,采用JESD22-B103B[15-16]標準里的加速度功率譜密度PSD 對模塊施加載荷,如表2 所示。

表2 加速度功率譜輸入值Tab.2 Input value of acceleration power spectrum

在隨機振動分析引擎中選定材料以及加載測試數據中的載荷譜數據,在分析模塊中設置采用Miner 累計損傷法則,對結構進行累積損傷計算,確定循環次數,得到結構的疲勞壽命。Data Value Display 顯示結構上各節點的疲勞數據,FEDisplay 顯示結構損傷、壽命云圖等。nCode 隨機振動疲勞壽命分析流程如圖7所示。

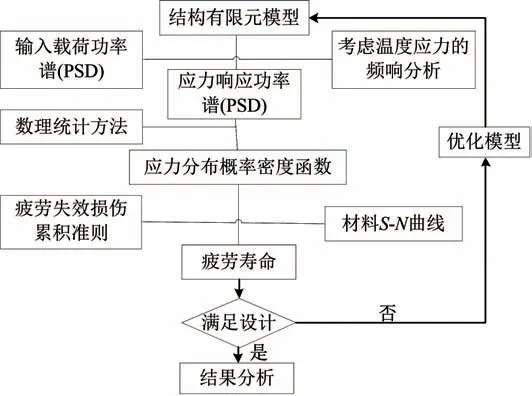
圖7 nCode 隨機振動疲勞壽命分析流程Fig.7 nCode random vibration fatigue life analysis process

3.2 常溫與受熱條件下的振動疲勞壽命計算和分析

分別將前面常溫下及導入熱應力載荷的結構有限元分析結果作為輸入載荷,使用nCode 軟件計算模塊在施加激勵機械載荷和溫度載荷作用下的疲勞壽命。nCode 軟件可以對影響疲勞的因素進行插值修正或影響因子修正處理,其中溫度對材料性能曲線影響取決于溫度對材料的極限抗拉強度(UTS)的影響。以鍵合線鋁材為例,查找nCode 軟件材料庫可知鋁材的S-N曲線如圖8 所示,該材料數據來自于美軍用手冊MILHDBK-5H[17]。

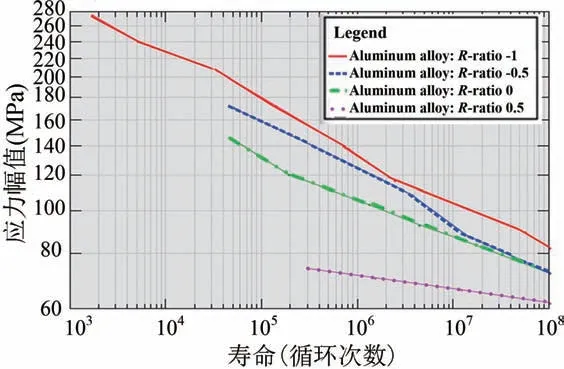
圖8 Al 材料S-N 曲線Fig.8 S-N curves of Al materials

設定材料參數、加速度功率譜密度PSD,進行統計學累積損傷等參數配置與運行,得到疲勞壽命云圖及疲勞損傷云圖,如圖9 所示。

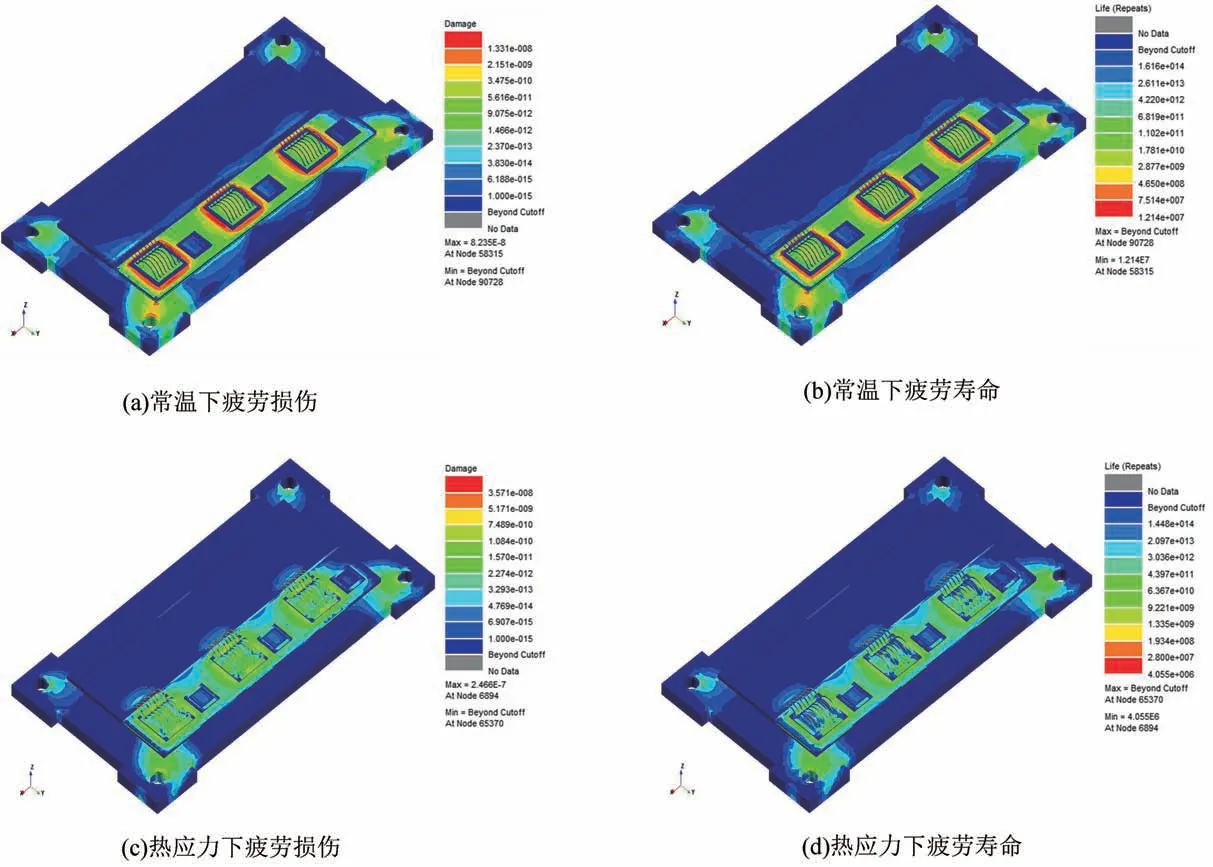
圖9 模塊的疲勞損傷及壽命云圖Fig.9 Fatigue damage and life nephogram of module

由圖9 可知,模塊危險部位發生在模塊IGBT 芯片位置處,除了個別節點因為模型細節處集中應力問題而壽命較低以外,其他節點壽命在常溫條件下普遍在1.21×107個循環以上;電-熱-機械組合工況下最早失效發生在鍵合線的鍵合處,最小循環次數為4.05×106,其次是芯片焊料層,最小循環次數為1.18×107。這與靜力分析結果及實際使用時IGBT 模塊疲勞破壞高發位置相同,同時可說明IGBT 模塊為低應力狀態下的高周疲勞破壞。與常溫疲勞危險點壽命對比,考慮熱應力影響下的疲勞壽命值明顯降低,因此在疲勞設計階段應充分考慮溫度分布的影響。

4 結論

本文對某種型號的高壓大功率IGBT 分別進行了常溫條件下與電-熱-機械耦合下的振動疲勞壽命分析。通過計算對比發現,溫度升高引起的模塊材料的各項參數發生變化使得材料力學性能退化,導致頻率響應分析得到的應力傳遞函數發生相應的改變,響應應力幅值、峰值頻率及振動疲勞壽命均發生了不同程度的變化。經過考慮熱應力的壽命評估更合理。

本文提出了一種壽命評估方法,主要結論如下:

(1)考慮熱應力對結構模態的影響,發現熱模態下的各階固有頻率均有不同程度的下降,建議在設計階段考慮溫度場分布對結構模態的影響,避免共振發生。

(2)IGBT 模塊的熱應力計算結果顯示,各部分等效應力遠小于材料屈服強度,僅從傳統靜力破壞角度考慮,在此工況下IGBT 模塊整體符合傳統靜力強度要求,是安全的。

(3)IGBT 模塊壽命最薄弱的部分在芯片、鍵合線及芯片焊料層,基于nCode 的考慮熱應力下的疲勞壽命比較不考慮熱應力的振動疲勞壽命有所降低,但總損傷小于1,均高于設計壽命,滿足鐵路牽引系統中IGBT 模塊的使用壽命及失效率要求。熱機耦合作用對疲勞壽命影響顯著,不可忽視。