鄭州市降雨-徑流關系不確定性分析

張金萍，王宇昊

(1.鄭州大學水利科學與工程學院，河南 鄭州 450001； 2.中國氣象科學院災害天氣國家重點實驗室，北京 100081；3.鄭州大學黃河生態保護與區域協調發展研究院，河南 鄭州 450001)

正確認識降雨-徑流之間的關系，可以識別下墊面的水文效應和氣候變化的水文效應，是區域水文模型構建的基礎[1]。隨著人類活動的加劇，降雨-徑流關系不確定性增加，對變化環境下降雨-徑流關系的研究具有重要的意義。近年來，許多人對降雨-徑流關系進行了研究，如，張學成等[2]運用動態分析研究了黃河流域劃分的11個區域進行了降雨-徑流關系的動態變化特點；郭愛軍等[3]利用滑動偏相關系數法診斷涇河流域降雨-徑流關系變異情況，并引入Copula函數分析降雨-徑流關系變化特征；高申等[4]以汾河水庫流域為例,運用M-K檢驗和集對分析的方法,分析了水土保持對降雨與徑流關系的影響。這些研究主要集中于降雨-徑流關系的突變及變化趨勢上，但降雨-徑流關系具有動態性，人類活動的動態變化時刻影響著降雨-徑流關系[5]，這些研究無法反映降雨和徑流之間在不同時間尺度下的聯系。本文以鄭州市年降水量和年徑流量數據序列為基礎，利用累積距平法對降雨和徑流進行趨勢分析，結合滑動t檢驗法確定徑流突變年份作為降雨-徑流關系的突變點，再分別對長序列的鄭州市年降水量、年徑流量進行多時間尺度小波分析，最后對不同時間尺度下和不同時段的降雨-徑流進行集對分析。

1 研究區概況及數據來源

鄭州市位于河南省中部，北臨黃河，西依嵩山，東南為廣闊的黃淮平原。全市東西長135～143 km，南北寬70～78 km，總面積7 446 km2。鄭州市屬北溫帶大陸性季風氣候，冷暖氣團交替頻繁，四季分明，年平均氣溫14.3 ℃，全市多年平均降水量 635.6 mm。鄭州市地跨黃河、淮河兩大流域，其中黃河流域面積2 012 km2，淮河流域面積5 434 km2，全市大小河流124條，流域面積較大的河流有29條，其中黃河流域6條，淮河流域23條。

本文選用鄭州市及周邊的50個雨量站的年降水量加權平均后作為鄭州市年降水量序列；告成、中牟、新鄭3個水文站的年徑流量之和作為鄭州市年徑流量序列，其中告成站位于穎河，中牟站位于賈魯河，新鄭站位于雙洎河。研究區域內主要河流和站點分布見圖1。

(a) 雨量站

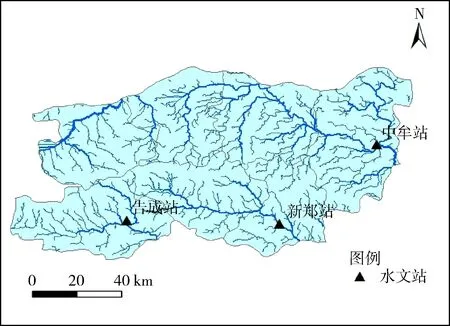
(b) 主要河流及水文站

2 研究方法

2.1 滑動t檢驗

滑動t檢驗根據滑動點和步長對序列逐點進行t檢驗，即設滑動點前為序列1，滑動點后為序列2，從兩序列中抽取容量分別為n1和n2的樣本，對兩序列的分布函數相等這一假設進行檢驗[6]，則

(1)

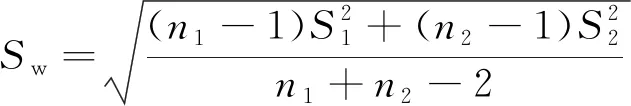
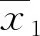
T服從t(n1+n2-2)分布，對于給定的顯著性水平α，當|T|>tα/2時原假設被拒絕，即抽取的兩個樣本存在顯著性差異，序列發生突變[7]。

2.2 小波變換

小波變換的基本思想是用一簇小波函數系來表示逼近某一信號或函數[8]。因此，小波函數是小波變換的關鍵，它是指具有震蕩性、能夠迅速衰減到0的一類函數[9]，即

(2)

式中ψ(t)為基小波函數，它可通過尺度的伸縮和時間軸上的平移構成一簇函數系。

(3)

式中：ψa,b(t)為子小波；a為尺度因子，反映小波的周期長度；b為平移因子，反映時間上的平移。對于給定的能量有限信號f(t)∈L2(R),其連續小波變換為

(4)

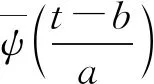
(5)

由式(5)可知小波變換的基本原理，即通過增加或減小伸縮尺度a來得到信號的低頻或高頻信息，分析信號的概貌或細節，實現對信號不同時間尺度和空間局部特征的分析[10]。

2.3 集對分析法

集對分析是對不確定系統中有關聯的兩個集合構造集對，二者等級水平相同的即為同一，相差一級的即為差異，相差兩級的為對立。做同一性、差異性、對立性分析，然后用聯系度描述集對的同、異、反關系[11]。

(6)

其中N=S+F+Le=S/N

f=F/Ng=L/N

式中：μ為兩個集合的聯系度，聯系度越大，二者關系越密切；S為同一性個數；F為差異性個數；L為對立性個數；N為集合的總長度；i為差異性系數，i的取值范圍為[-1,1]，本文中i取0.5；j為對立性系數，j值常取-1；e、f和g分別為兩個集合的同一度、差異度和對立度[12]。

3 結果與分析

3.1 降雨-徑流關系變化趨勢

圖2為1963—2012年鄭州市年降水量和年徑流量變化，可見，1963—2012年，鄭州市年降水量變化線整體圍繞多年平均降水量上下波動，而年徑流量變化沒有明顯的規律，二者的變化趨勢在大部分時段內基本一致，存在若干時段高度一致或變化趨勢相反。

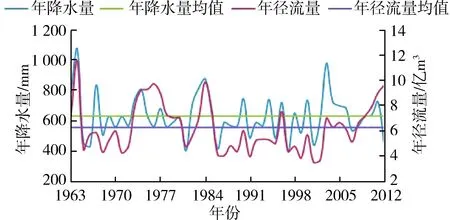
圖2 1963—2012年鄭州市年降水量和徑流量變化

為進一步研究年降水量和年徑流量的變化趨勢，對降雨和徑流序列作累積距平[13]曲線(圖3)。由圖3可見，鄭州市年降水量增減不定，呈現出3～5 a的周期變化，整體上沒有明顯的變化趨勢；1965—1972年，鄭州市年徑流量始終低于多年均值；1972、1985、2002年徑流趨勢發生改變且1973—1984年，2003—2012年兩時段內年徑流量基本高于多年均值，而1985—2002年時段內年徑流量基本低于多年均值。

圖3 鄭州市降雨-徑流累積距平曲線

為了進一步確定徑流的突變年份，利用滑動t檢驗法，分別取步長為5 a、7 a、10 a，取顯著性水平為0.01，查表得臨界值依次為3.355、3.055、2.878，對年徑流量進行突變分析，結果見圖4。由圖4可見，n1=n2=5 a時，年徑流量在1972年、1977年、2002年發生突變；n1=n2=7 a時，年徑流量在1972年、1985年、2003年發生突變；n1=n2=10 a時，年徑流量在1985年、2002年發生突變。

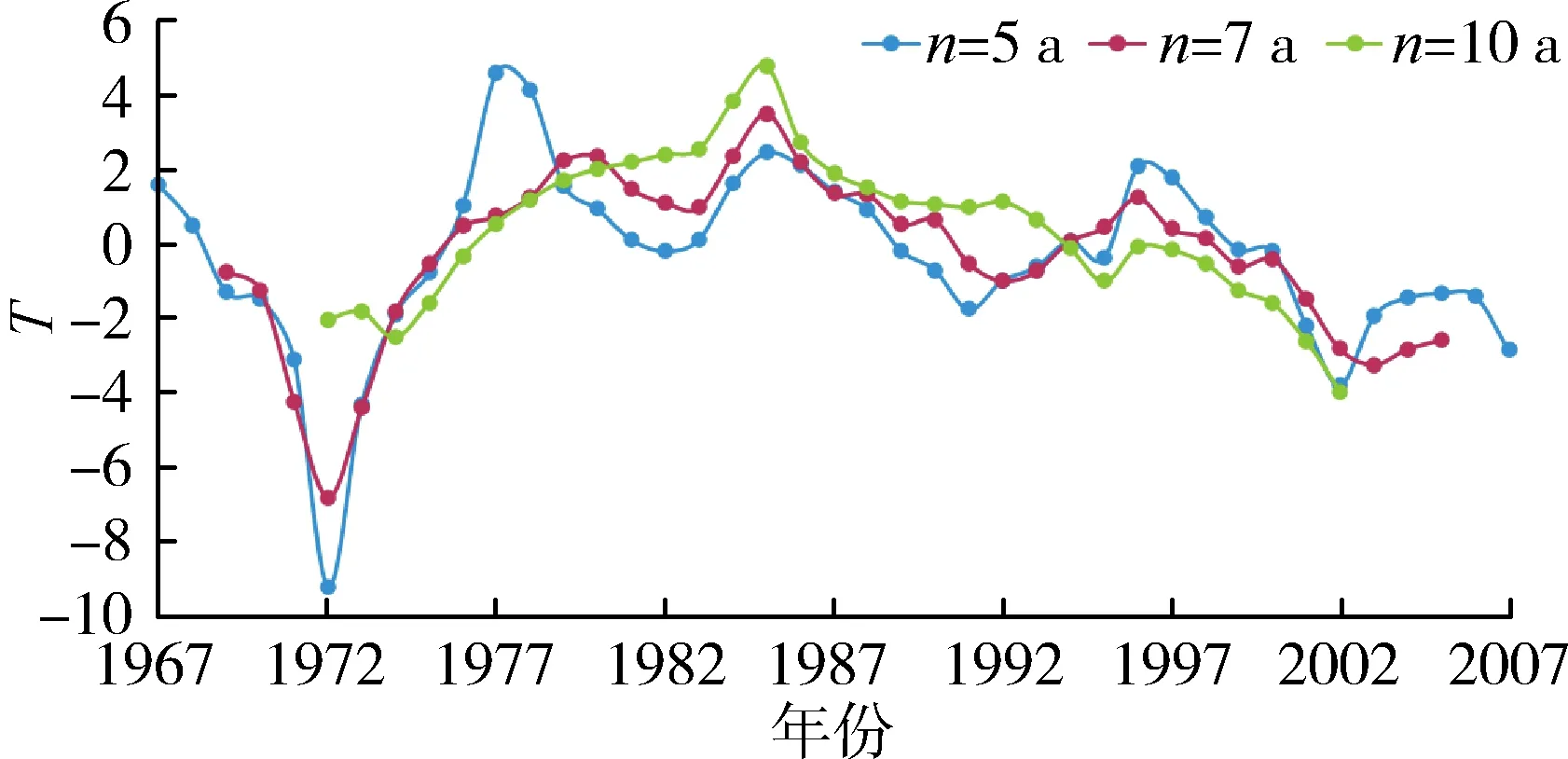
圖4 鄭州市年徑流量滑動t檢驗曲線

由于滑動t檢驗默認前后兩序列樣本容量相等，存在一定的局限性[14-15]，因此假設1972年、1985年、2002年為徑流突變年份，與突變點劃分時段的長度不一致，因此對根據假設突變點劃分的時段，對突變點進行進一步t檢驗，見表1。

由表1結合圖4可得：①在99%的置信度下，1985年、2002年為鄭州市徑流突變年份，且1985年的突變最為顯著，由于鄭州市降雨無明顯變化趨勢，則徑流量的突變年份即為降雨-徑流關系發生改變的年份；②1985年徑流量發生減小突變，說明人類活動對徑流量影響顯著，根據實際情況分析，這一結果可能是1985年后鄭州市社會經濟高速發展，人口急劇增長，城市取用水量增大所導致的；③2002年徑流量發生增大突變，結合實際情況，可能是因為進入21世紀以來鄭州市城市化程度不斷提高[16]，不透水面積增大導致下滲量減小，從而使徑流量增大[17-18]。

表1 突變點的顯著性t檢驗

3.2 降水量和徑流量的小波分析

選用緊支集正交小波(db6)[19-22]，對年降水量和年徑流量序列進行一維離散小波分析。圖5、圖6分別為二者分解所得的分量，其中Pa5分量可體現年降水量整體的變化趨勢，Ra5分量體現年徑流量整體的變化趨勢。從圖5、圖6可以看出：①鄭州市降水量分量Pd1具有準2～4 a波動周期，波動幅度逐漸減小，至今較為平穩；分量Pd2具有準5～7 a波動周期，波動幅度總體變化趨勢散亂；分量Pd3具有準6～11 a 波動周期，前期波動幅度較為平緩，2005—2012年波動幅度減小；分量Pd4具有準23 a波動周期；分量Pd5具有準32 a波動周期。②鄭州市徑流量的分量Rd1具有準2～4 a波動周期，波動幅度在20世紀60年代中期較大,之后至今波動幅度較為平穩；分量Rd2具有準4～9 a波動周期，波動幅度在20世紀80年代較大,其他時段波動幅度較為平穩；分量Rd3具有準8～11 a波動周期，波動幅度從20世紀80年代開始逐漸減小；分量Rd4具有準17 a波動周期，波動幅度呈減小趨勢。③年降水量呈現逐漸減小的趨勢；年徑流量呈現先減后增的趨勢，且在20世紀80年代末達到最小值。

(a) d1～d5分量

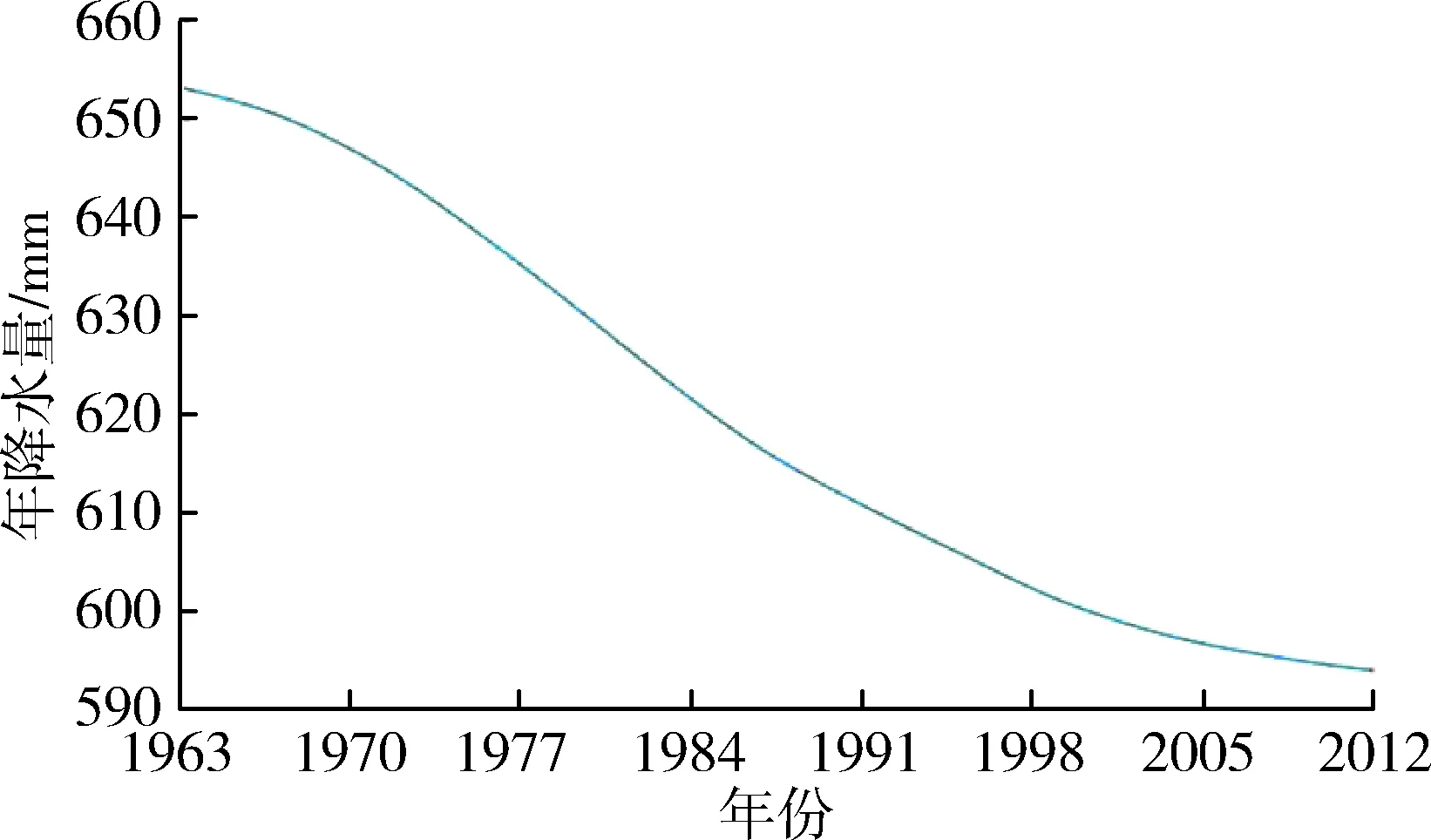
(b) a5分量

(a) d1～d5分量

(b) a5分量

3.3 降水量與徑流量的多時間尺度集對分析

根據小波變換多時間尺度的分析結果，設定 2～4 a為短周期,5～9 a為中周期，10～16 a為中長周期，17～23 a為長周期，將降水量的各細節成分序列與徑流量的各細節成分序列分別進行多時間尺度集對分析。采用均值標準差法，降水量和徑流量分級標準分別見表2和表3。

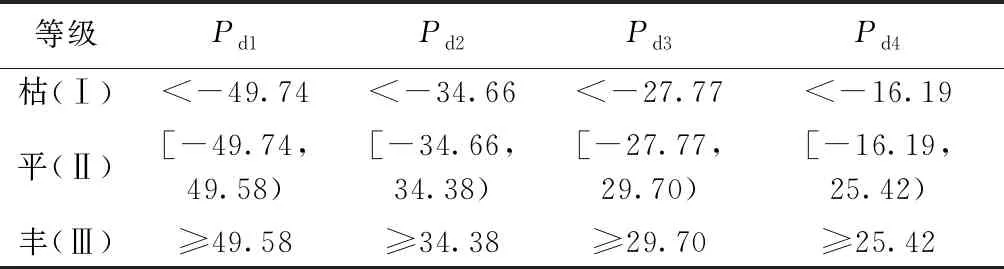
表2 降水量分級標準

構建4個集對：H(Pd1,Rd1)、H(Pd2,Rd2)、H(Pd3,Rd3)、H(Pd4,Rd4)。計算每一集對的同一度、差異度、對立度和聯系度，計算結果見表4。從表4可見，鄭州市降水量和徑流量的同一度主要表現在短周期尺度上，差異度主要表現在中長周期尺度上，對立度主要表現在長周期尺度上。鄭州市降雨和徑流的相關程度在中周期尺度和中長周期尺度上最高，在長周期尺度上最小。鄭州市年降水量和年徑流量在短、中、中長周期以同一性為主，差異性同樣占主要位置，對立性可忽略不計；在長周期則以差異性為主，且此時對立性較同一性占主要位置。

表3 徑流量分級標準

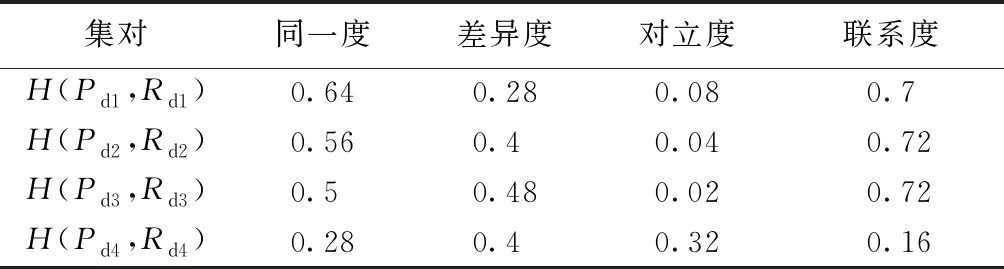
表4 鄭州市降雨-徑流多時間尺度集對分析結果

同理，對1963—1984年、1985—2001年、2002—2012年3個時段的降雨徑流進行集對分析(表5)。將鄭州市各時段降雨-徑流集對分析結果與多時間尺度集對分析結果進行比較可得，1963—1984年這一時段鄭州市降雨-徑流關系與長周期尺度下的降雨-徑流關系一致性較高；1985—2001年這一時段鄭州市降雨-徑流關系與中長周期尺度下的降雨-徑流關系一致性較高；2002—2012年這一時段鄭州市降雨-徑流關系與中周期尺度下的降雨-徑流關系一致性較高。

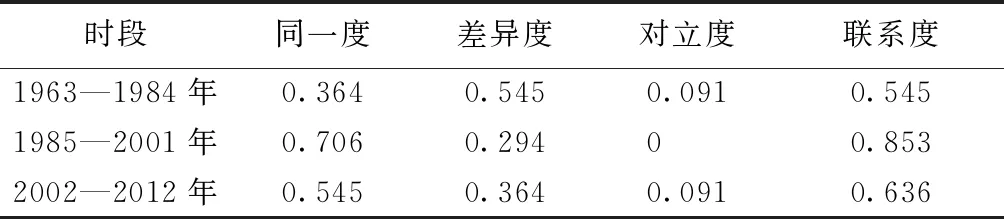
表5 各時段降雨-徑流集對分析結果

4 結 論

a.鄭州市降雨-徑流關系在1985年和2002年發生顯著改變，人類活動對徑流影響愈發顯著，徑流的影響因素增多，降雨-徑流關系的不確定性增加。根據突變年份劃分為3個時段：1963—1984年、1985—2001年、2002—2012年，其中第二時段二者相關程度最大，第一、第三時段二者相關程度較小。

b.鄭州市年降水量具有準2～4 a、5～7 a、6～11 a、23 a、32 a的波動周期；年徑流量具有準2～4 a、4～9 a、8～11 a、17 a的波動周期，反映了降雨-徑流關系的復雜性。

c.鄭州市年降水量和年徑流量在短、中、中長周期以同一性為主，差異性同樣占主要位置，對立性可忽略不計；在長周期則以差異性為主，且此時對立性占主要位置。這一規律可為從宏觀和微觀角度預測鄭州市徑流、研究鄭州市下墊面和氣候變化等方面提供理論支撐。