基于集合經驗模態分解和ARIMA-GRNN的負荷預測方法

王洪亮，陳新源，趙雨夢

(昆明理工大學 電力工程學院,云南 昆明 650500)

智能電網作為研究熱點受到越來越多的關注。用戶是電網服務的對象，在智能電網中發揮著至關重要的作用。對用戶側數據進行采集、傳輸和存儲，有利于管理電網發電需求。對用戶負荷數據進行管理可以使電網更加安全可靠地運行[1]。電力負荷預測在保證電力系統安全及經濟運行方面具有重要意義。進行負荷預測，需要建立與之對應的數學模型。隨著負荷預測理論研究的不斷深入，電力負荷預測的理論和方法也越來越多，例如神經網絡、模糊理論、小波分析等[2]。但是這些方法仍具有局限性，例如神經網絡算法要按照一定的準則進行學習，然后才能工作，而且容易出現陷入局部極小的現象。目前已有的負荷預測理論方法已無法滿足預測速度和精度的要求，當計算數據非常龐大時，傳統方法就顯得力不從心，通常耗時幾小時甚至幾天。隨著智能電網的發展，需要進行海量數據的收集、存儲和處理，因此亟需一種新的大數據處理方法[3]。新型負荷的出現也對電網提出更高的要求，在大量數據基礎上進行數據預測就顯得十分重要[4]。在上述背景下，本文提出一種基于集合經驗模態分解和ARIMA-GRNN的混合負荷預測模型，兼顧了電力負荷內在的線性特征與非線性特征，可以對電力系統負荷預測進行有效分析。仿真結果表明，該模型算法較之傳統單一算法效果更加優越。

1 集合經驗模態分解算法

經驗模態分解(Empirical Mode Decomposition，EMD)法是一種新型自適應信號時頻處理方法，適用于非線性非平穩信號的分析處理。EMD法依據數據自身的時間尺度特征來進行信號分解，無須預先設定基函數。集合經驗模態分解方法(Ensemble Empirical Mode Decomposition，EEMD)是在EMD方法的基礎上發展起來的[5]。該方法的本質是對時間序列數據進行局部平穩化處理，再進行希爾伯特變換獲得時頻譜圖，從而得到有物理意義的頻率[6]。EEMD的思想是信號極值點影響固有模態函數(Intrinsic Mode Function，IMF)分量，若分量分布不均勻則會出現模態混疊。將頻譜均勻分布的白噪聲引入要分析的信號中，可使信號自動分布到合適的參考尺度上。集成均值的計算結果與原始信號的差值隨著集成平均次數的增加而減少[7]。由于零均值噪聲的特性，噪聲經過多次平均計算后會相互抵消，因此可將集成均值的計算結果視作最終結果。

EEMD算法步驟如下：

步驟1將正態分布的白噪聲加到原始信號；

步驟2將加入白噪聲的信號作為一個整體，然后進行EMD分解，得到各IMF分量；

步驟3重復步驟1和步驟2，每次加入新的正態分布白噪聲序列；

步驟4將每次得到的IMF做集成平均處理后的結果作為最終結果。

由于受到天氣變化、經濟波動等多種外界因素的影響，負荷通常呈現非平穩序列的特征，所以必須對其采取平穩化處理。為了得到理想的預測結果，在數據進入模型的訓練過程之前，需要對電力負荷的原始數據進行處理和分析。由于傳統的信號分解方法對于分解非線性非平穩的負荷序列存在較大的局限性，故本文采用EEMD對原始負荷序列進行分解。

2 傳統負荷預測方法

2.1 ARIMA時間序列模型

ARIMA為差分自回歸滑動平均模型，又稱為求自回歸滑動平均模型，是時間序列預測分析方法之一。ARIMA時間序列法被廣泛應用于電力系統負荷預測。該方法只需要通過前期的負荷數據便可以構建基于時間的數學模型，不僅計算速度快，計算過程簡單，且只需少量數據就可以對平穩序列達到較高的預測精度。但是，如果負荷數據為非平穩序列，則需要在使用該方法前先實施平穩化處理[8]。

如圖1所示，ARIMA模型是自回歸模型AR模型和MA模型的整合模型，是一種常用的時間序列預測模型。其模型具體形式為

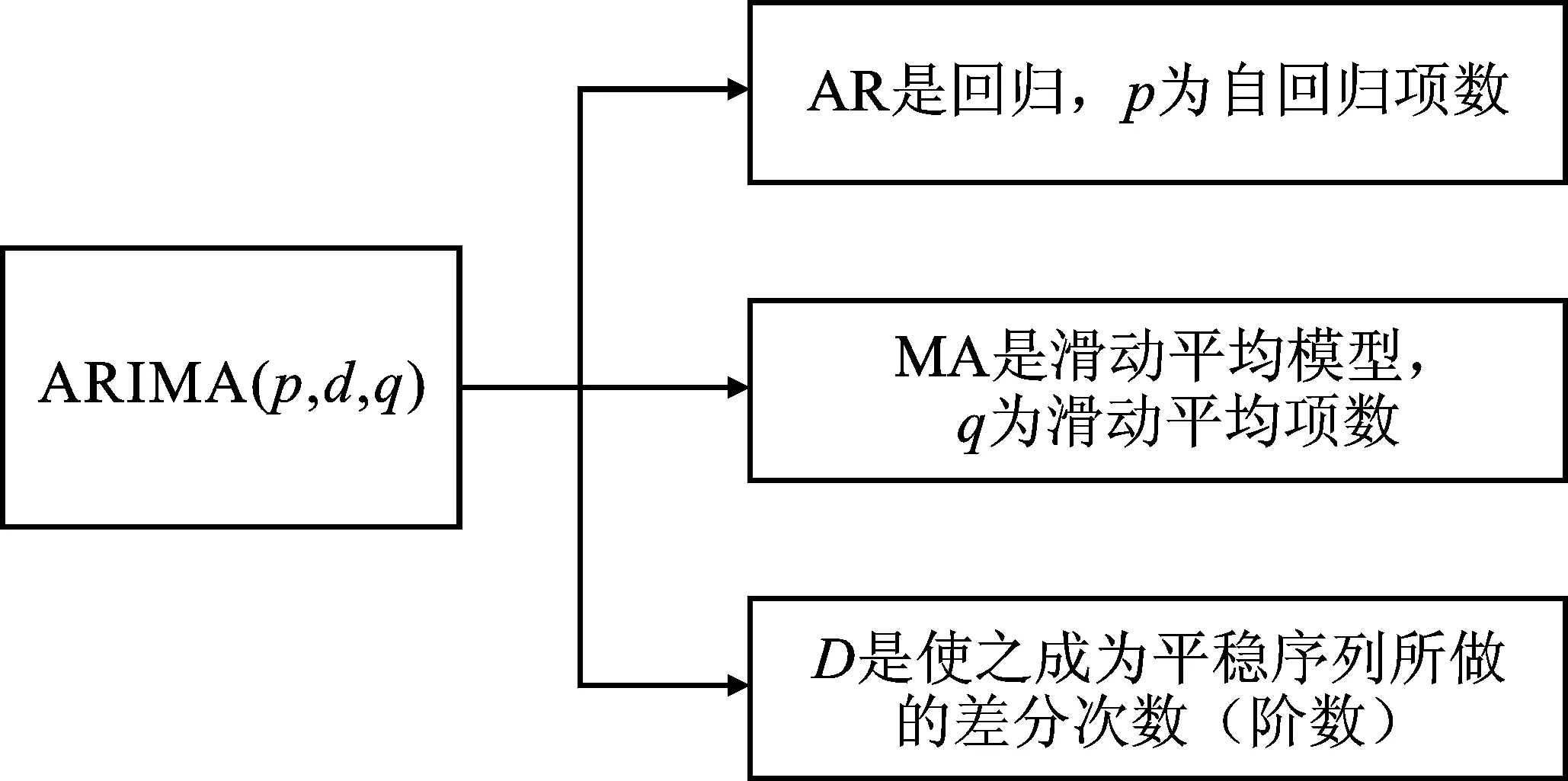
圖1 ARIMA結構圖Figure 1.ARIMA structure diagram

(1)

式中，t表示時間；yt為隨時間t變化的原始負荷時間序列數據；Δdyt表示yt經d次差分后的平穩時間序列；εt表示隨時間t變化的零均值的白噪聲隨機誤差序列；Φi為AR模型第i階的估計參數；p為AR模型的最佳階數；θj為MA模型第j階的估計參數；q為MA模型的最佳階數。

基于ARIMA時間序列建模步驟如圖2所示。如果負荷數據是一個非平穩的時間序列，則首先需要對時間序列做d階差分，得到一個平穩的時間序列[9]。然后，對自回歸階數和滑動平均階數嘗試取值進行參數估計，利用AIC、BIC、HQC等信息準則挑選出最優的ARIMA預測模型。最后，利用挑選出來的最優ARIMA預測模型對負荷時間序列進行預測分析[10]。

圖2 ARIMA建模圖Figure 2.ARIMA modeling diagram

2.2 GRNN神經網絡負荷預測算法

廣義回歸神經網絡(Generalized Regression Neural Network，GRNN)是一種徑向基神經網絡，具有很強的非線性映射能力和學習速度。GRNN最后收斂于樣本量集聚較多的優化回歸，當樣本數據較少時，預測效果較好，還可以處理不穩定數據[11]。雖然GRNN沒有徑向基精準，但在實際分類和擬合方面，特別是在數據精準度比較差的時候，GRNN有著很大的優勢[12]。

電力負荷預測是一個受諸多因素影響的具有隨機性、非線性、動態不確定性的過程，對預測精度有一定的要求。針對天氣、溫度等隨機因素對電力負荷的復雜影響，采用GRNN神經網絡算法實現多種隨機因素影響的短期電力負荷預測。由于GRNN神經網絡具有較強的魯棒性、非線性和自適應等特性，因此可以利用神經網絡的學習能力來學習歷史數據中包含的映射關系，再利用這種映射預測未來的電荷。

其中，X(x1,x2,…,xn)為輸入；Y(y1,y2,…,yn)為輸出。

如圖3所示，GRNN神經網絡結構包括輸入層、模式層、求和層和輸出層。輸入層為向量，維度為m，樣本個數為n，線性函數為傳輸函數。隱藏層與輸入層全連接，層內無連接，隱藏層神經元個數與樣本個數相等，也是n，傳輸函數為徑向基函數。求和層中有兩個節點：第一個節點為每個隱含層節點的輸出和；第二個節點為預期的結果與每個隱含層節點的加權和。輸出層的輸出是第二個節點除以第一個節點的值[13]。

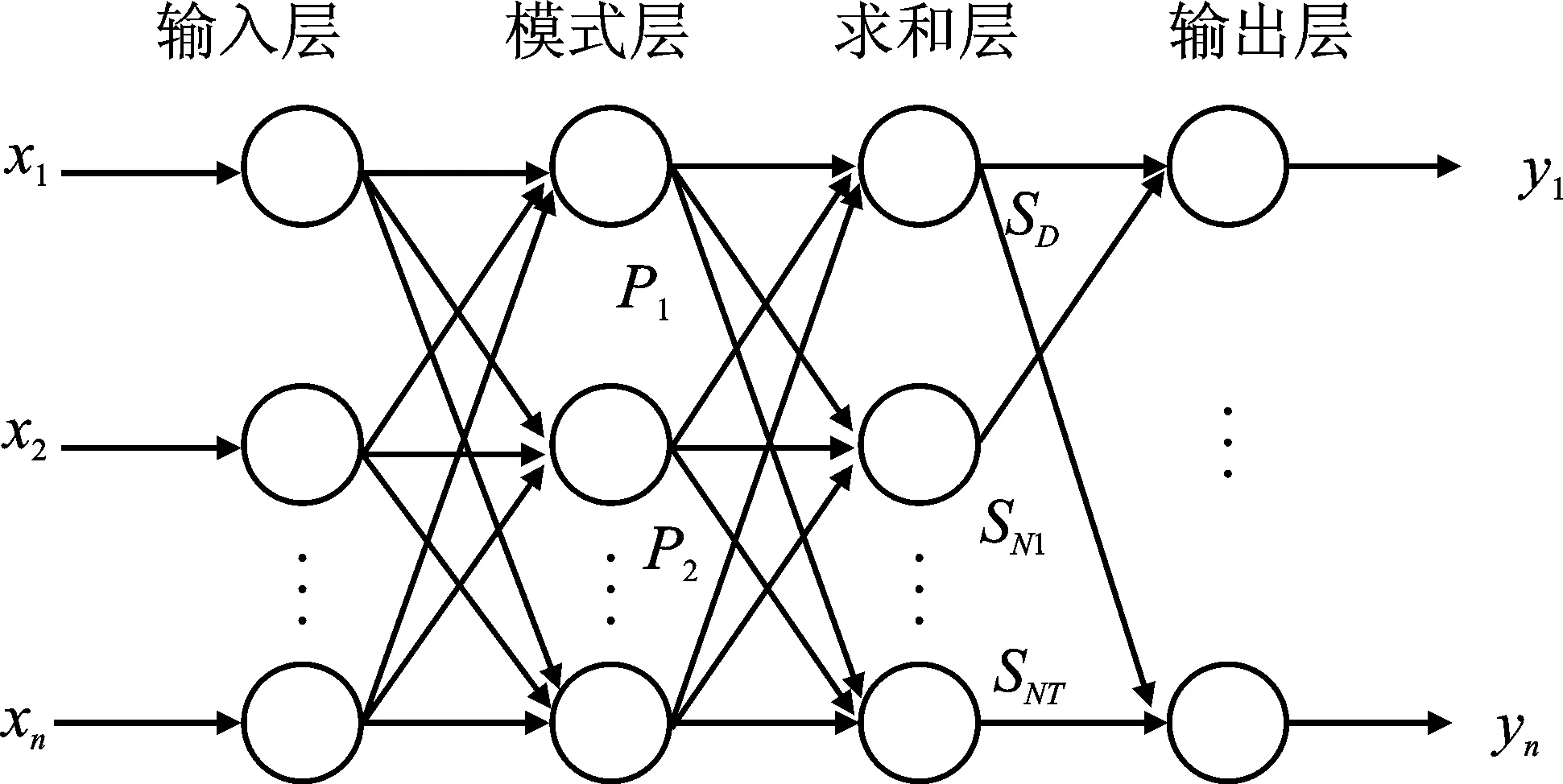
圖3 GRNN結構圖Figure 3.GRNN structure diagram

模式層函數為

(2)

式中，v為神經元；Pv為神經元v所在的模式層輸出；X為網絡輸入變量；Xv為第v個神經元學習樣本；σ為高斯函數的寬度系數，此處為光滑因子[14]。

求和層函數為

(3)

式中，n為神經元最大值；SD為求和層的輸出。

對所有模式層神經元的輸出進行算術求和，其模式層與各神經元的連接權值為1。

GRNN在逼近能力和學習速度上較其他神經網絡算法有一定優勢。GRNN最后收斂于樣本量積聚較多的優化回歸面，且在樣本數據較少時具有較好的預測效果[15]。

3 基于EEMD和ARIMA-GRNN混合模型的負荷預測

電力系統負荷需求不僅包含時間序列變量，也受到溫度、天氣、經濟等各種因素影響[16]，進而產生非線性變量，如下式所示

Zt=Tt+Xt

(4)

式中，Zt為t時刻的觀測值；Tt為t時刻的線性時間序列分量；Xt為t時刻的非線性預測分量預測值。

因此，無論是單一的時間序列算法還是非線性的神經網絡算法，其對電力負荷預測都存在一定的局限性[17]。EEMD適用于非線性非平穩信號的分析處理[18-19]。本文提出了一種基于集合經驗模態分解和ARIMA-GRNN混合模型的負荷預測方法，其具體建模過程如圖4所示。

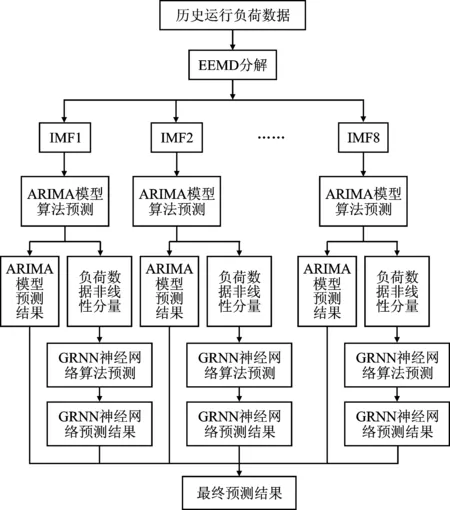
圖4 EEMD-ARIMA-GRNN模型算法建模圖Figure 4.EEMD-ARIMA-GRNN model algorithm modeling diagram

步驟1采用某地電網歷史運行負荷數據作為樣本原始數據，使用EEMD方法將樣本原始數據分解出不存在模態混疊的IMF分量和余項；

步驟2ARIMA(p,d,q)模型分為AR、I、MA共3部分。使用ARIMA(p,d,q)模型對每一項IMF分量進行預測，首先需確定數據的差分階數d。對樣本數據進行一次差分就能得到一個平穩的負荷時間序列。負荷需求往往受到一些外界因素如天氣或經濟的影響，所以歷史運行負荷數據一般表現為負荷數據時間非平穩時間序列；

步驟3對差分后平穩的IMF分量分別求得其自相關系數ACF和偏自相關系數PACF，通過對自相關圖的分析，得到最佳階層p。通過偏自相關圖的分析，得到最佳階數q。確定具體ARIMA(p,d,q)預測模型。利用選定的ARIMA預測模型對IMF分量進行預測分析得到預測數據。這些預測數據即為時間序列預測分量；

步驟4將通過步驟2得到的時間序列預測分量和樣本原始數據相減得到非線性分量數據。取歷史運行負荷每天的最高溫度、最低溫度、平均溫度、平均相對濕度和降雨量特征作為GRNN神經網絡算法的特征變量；非線性分量數據作為GRNN神經網絡算法訓練數據集和測試數據集。將訓練數據集輸入模塊進行訓練，反映這些特征變量對負荷的影響規律，得到訓練模型。再利用訓練模型對測試數據集進行測試，得到非線性預測分量預測值；

步驟5將所有時間序列預測分量和非線性預測分量兩者相加，即可得到具有更高精度的電力負荷預測值。

為了更加直觀地表明本文設計的復合模型的優越性，本文選取均方根誤差(Root Mean Square Error，RMSE)、平均絕對誤差(Mean Absolute Error，MAE)和平均絕對百分誤差(Mean Absolute Percentage Error，MAPE)3項數據來衡量預測模型的性能[16]。

RMSE是預測數據與實際數據差值平方和的算數平方根。均方根誤差用來描述數據序列的變化趨勢，其值越小，說明預測數值誤差越小，計算式如下

(5)

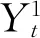
平均絕對誤差MAE和平均絕對百分誤差MAP可用來衡量預測算法性能，其值越小說明算法越好。

(6)

(7)

4 算例分析

4.1 基于ARIMA時間序列的負荷預測

選取某地電網歷史負荷數據，以2013年12月21日～2014年6月18日每天某個時刻共計180個數據作為樣本數據。使用ARIMA(p,d,q)模型進行預測，通過對負荷數據進行一次差分得到一個平穩的負荷時間序列，即d為1。對差分后平穩的負荷時間序列分別求得其自相關系數ACF和偏自相關系數PACF，得到最佳階層p為5，最佳階數q為8。確定具體ARIMA(5,1,8)，預測模型，進行預測分析得到預測數據，并與原始數據進行對比，得到原始數據與預測數據對比圖和相對誤差圖，如圖5和圖6所示。

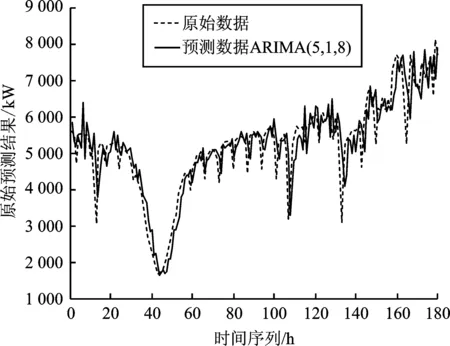
圖5 ARIMA模型算法預測圖Figure 5.ARIMA model algorithm prediction diagram

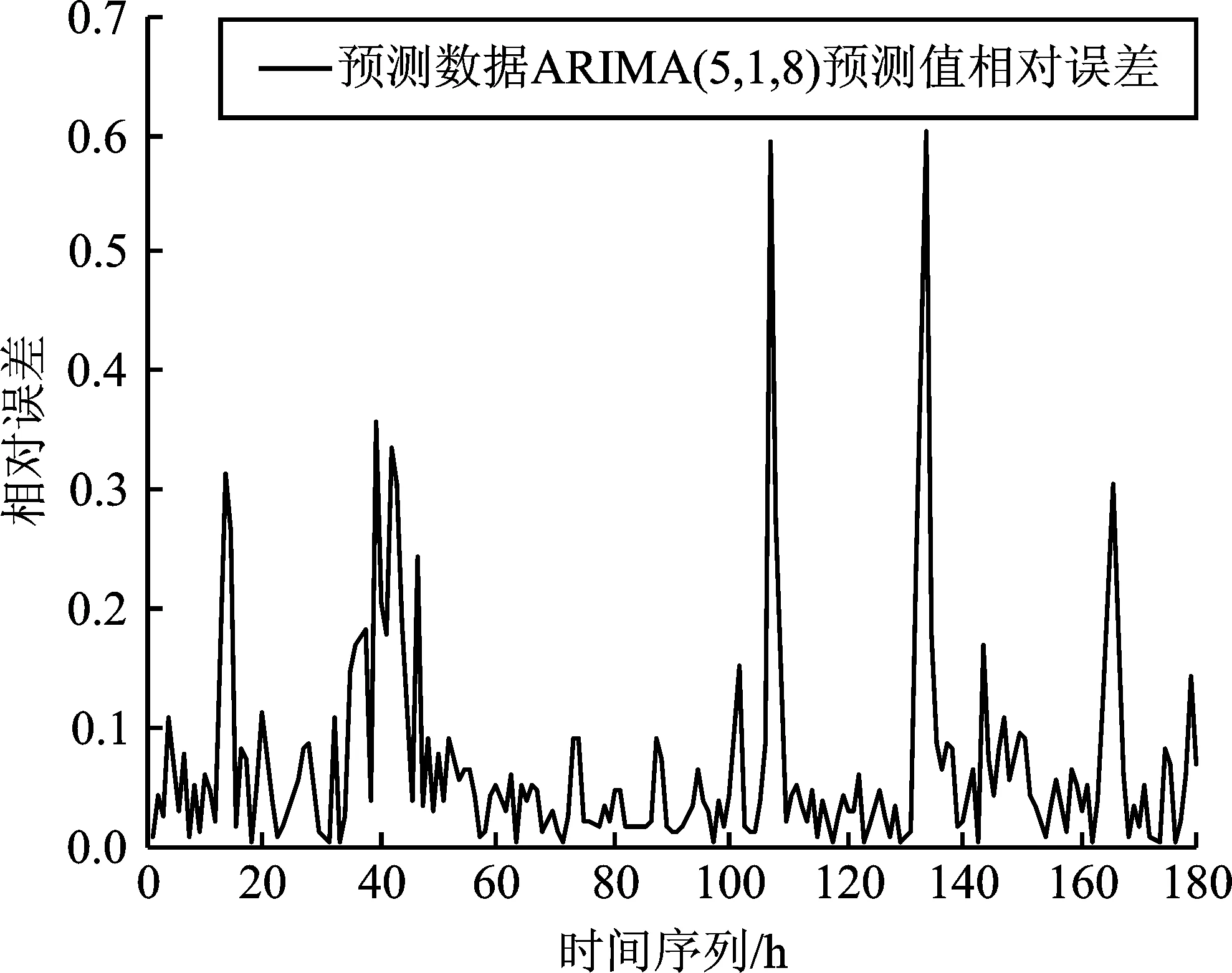
圖6 ARIMA模型算法相對誤差圖Figure 6.Relative error diagram of ARIMA model algorithm

采用基于ARIMA時間序列的負荷預測，其預測趨勢大致上與實際數據相同，但個別極值預測偏差過大，相對誤差達到0.6，即在突發的外界因素條件影響下，采用單一的ARIMA時間序列的負荷預測方法不能滿足預測精度要求。

4.2 基于GRNN神經網絡算法的負荷預測

本文以2012年1月1日～2014年6月18日每天某個時刻共計900個數據作為樣本數據，以2012年1月1日～2013年12月20日共計720個數據作為訓練數據，以2013年12月21日～2014年6月18日每天某個時刻共計180個數據作為測試數據。取負荷數據每天的最高溫度、最低溫度、平均溫度、平均相對濕度和降雨量特征作為GRNN神經網絡算法的特征變量，將訓練數據集輸入模塊進行訓練，反映這些特征變量對負荷的影響規律，得到訓練模型。然后，再利用訓練模型對測試數據集進行測試，得到預測值，并與原始數據進行對比，得到原始數據與預測數據對比圖和相對誤差圖，如圖7和圖8所示。

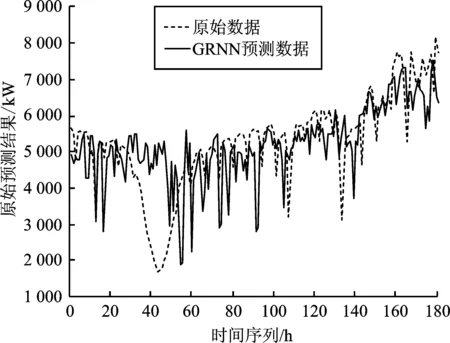
圖7 GRNN模型算法預測圖Figure 7.GRNN model algorithm prediction diagram

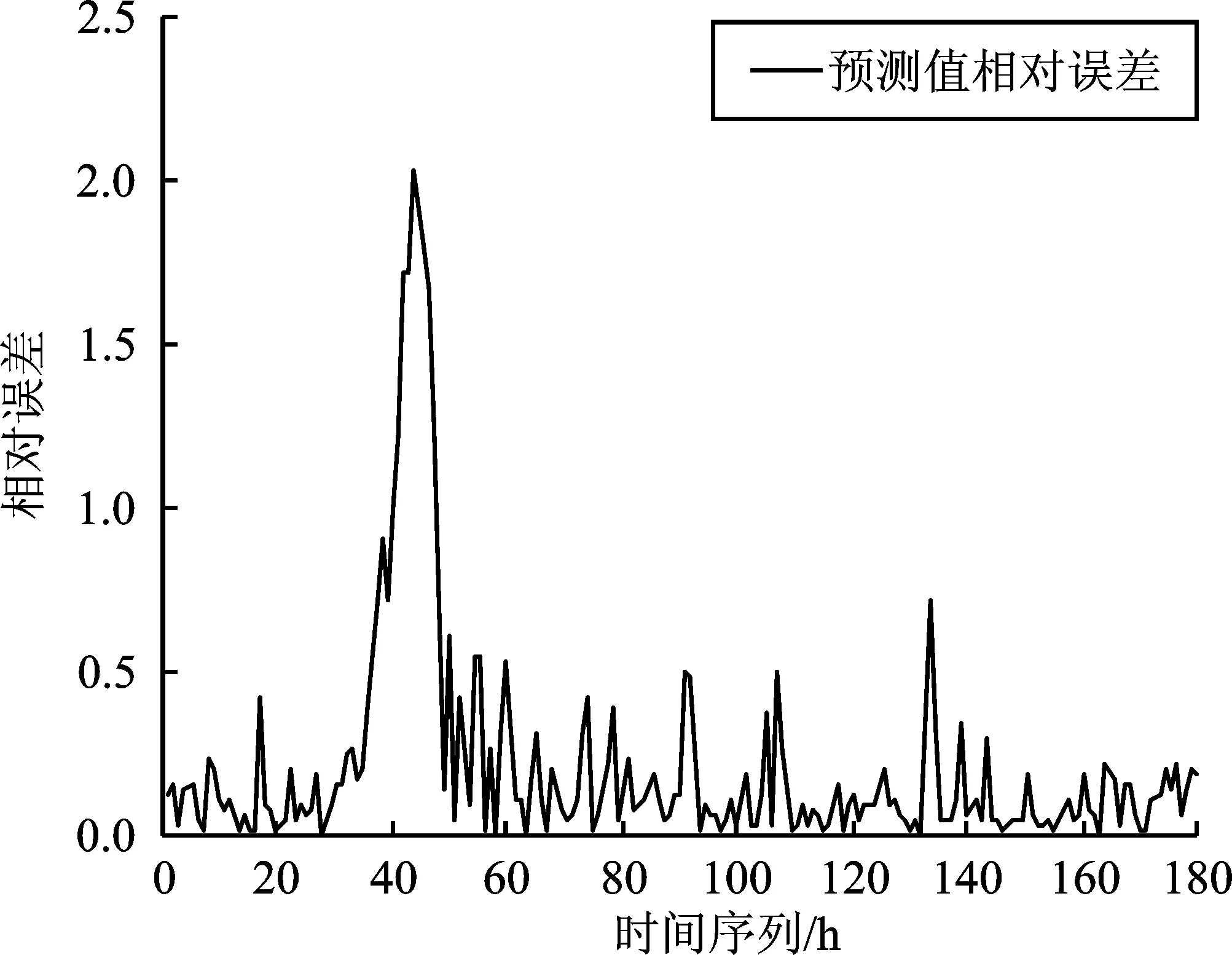
圖8 GRNN模型算法相對誤差圖Figure 8.Relative error diagram of GRNN model algorithm

基于GRNN神經網絡算法的負荷預測法的預測趨勢與實際數據有較大差距，無法滿足負荷隨時間線性變化的特征，說明單一的神經網絡算法同樣無法滿足負荷預測的精度要求。

4.3 基于ARIMA-GRNN混合模型的負荷預測

以2012年1月1日～2014年6月18日每天某個時刻共計900個數據作為負荷數據，先對其進行ARIMA模型預測，通過計算確定ARIMA(2,1,6)預測模型。然后，利用挑選出來的ARIMA預測模型對負荷數據進行預測分析得到線性預測數據，并與原始數據進行相減。將差值數據分為GRNN神經網絡算法訓練數據集和測試數據集，取負荷每天的最高溫度、最低溫度、平均溫度、平均相對濕度和降雨量特征作為GRNN神經網絡算法的特征變量。將訓練數據集輸入模塊進行訓練得到訓練模型，再利用訓練模型對測試數據集進行測試，得到非線性預測分量預測值。將非線性預測分量預測值和線性預測值相加得到最終預測值。原始數據與預測數據的對比圖和相對誤差圖如圖9和圖10所示。

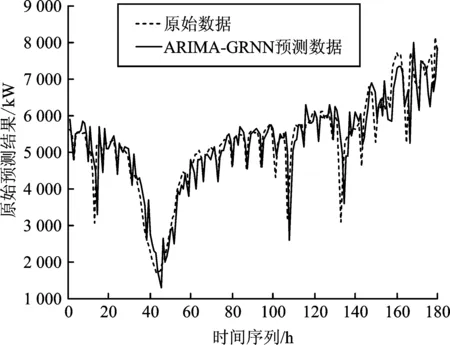
圖9 ARIMA-GRNN模型算法預測圖Figure 9.Algorithm prediction diagram of ARIMA-GRNN model

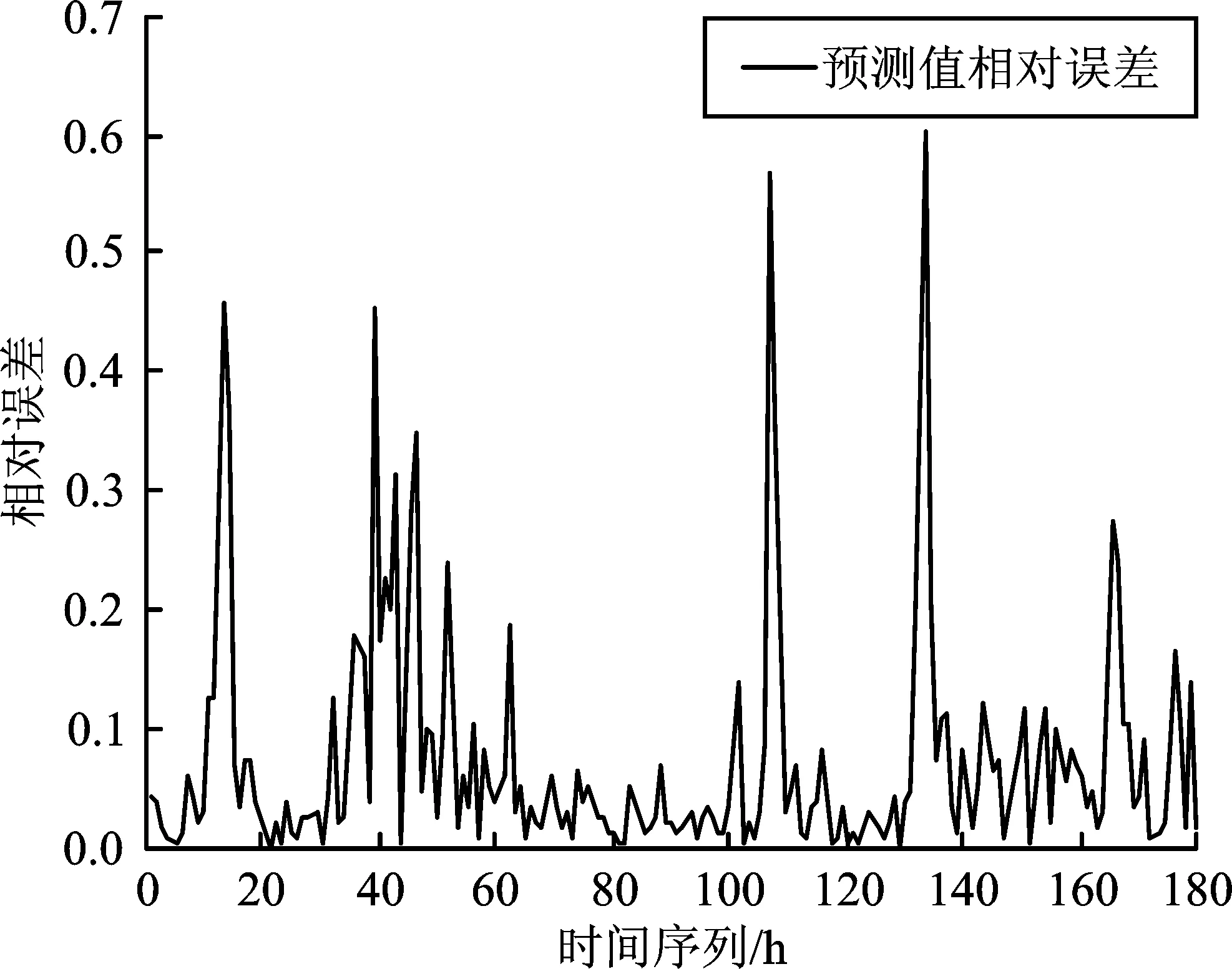
圖10 ARIMA-GRNN模型算法相對誤差圖Figure 10.Relative error chart of ARIMA-GRNN model algorithm

采用基于ARIMA-GRNN混合模型算法進行負荷預測，其預測趨勢大致與實際數據相同。相較于ARIMA方法，混合模型算法在負荷極點處的預測有了明顯的改善，基本滿足負荷預測的精度要求。

4.4 基于EEMD和ARIMA-GRNN混合模型的負荷預測

以2012年1月1日～2014年6月18日每天某個時刻共計900個數據作為樣本數據，加入100組試驗次數白噪音，白噪音標準偏差設置為0.2。通過EEMD將數據分解為IMF分量和余項，對每項IMF分量進行上述ARIMA-GRNN混合模型預測。將所有非線性分量與線性分量求和得到最終的預測值，如圖11～圖13所示。

圖11 負荷數據EEMD分解圖Figure 11.EEMD decomposition diagram of load data

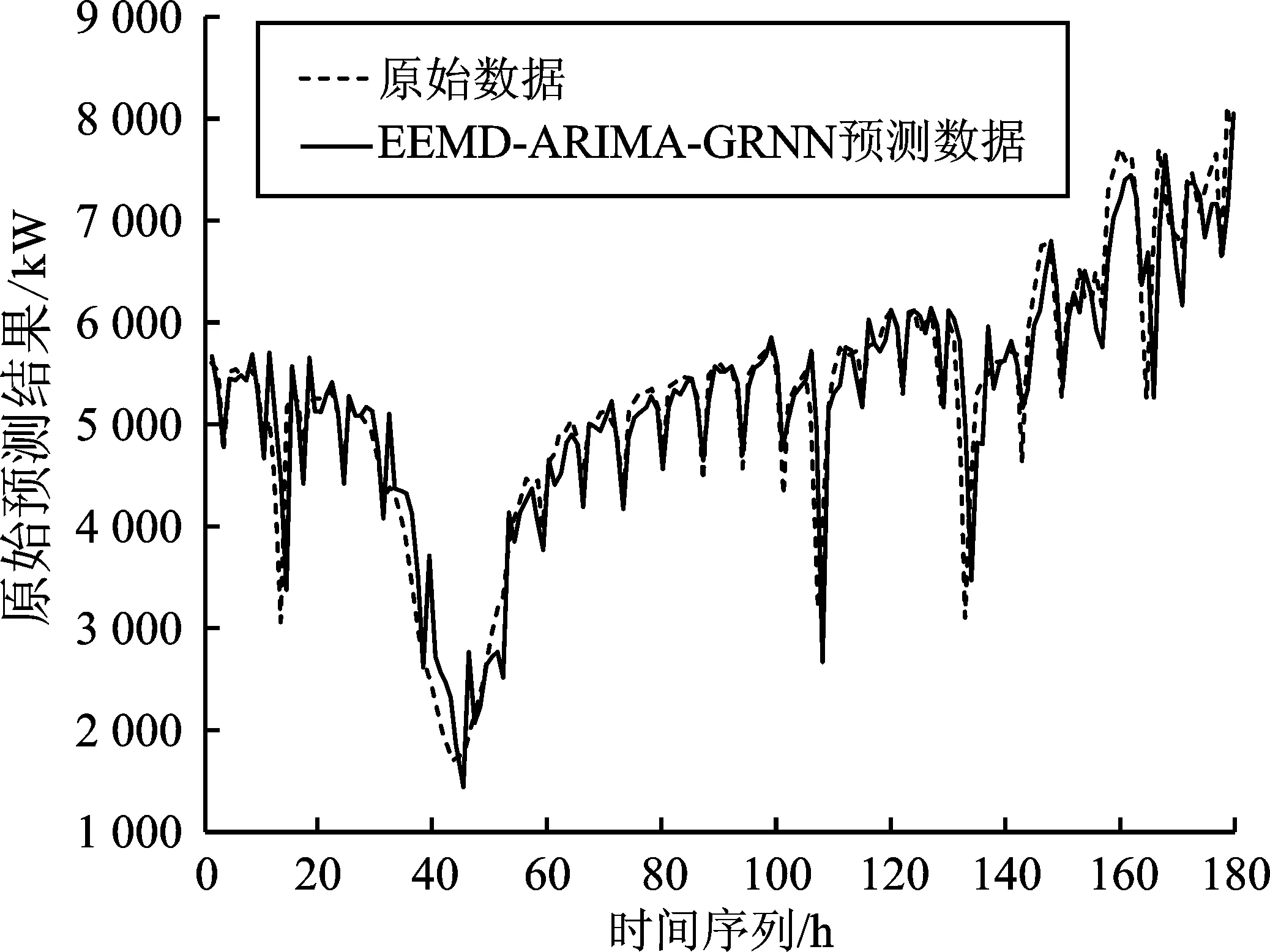
圖12 EEMD-ARIMA-GRNN模型預測圖Figure 12.Algorithm prediction diagram of EEMD-ARIMA-GRNN model

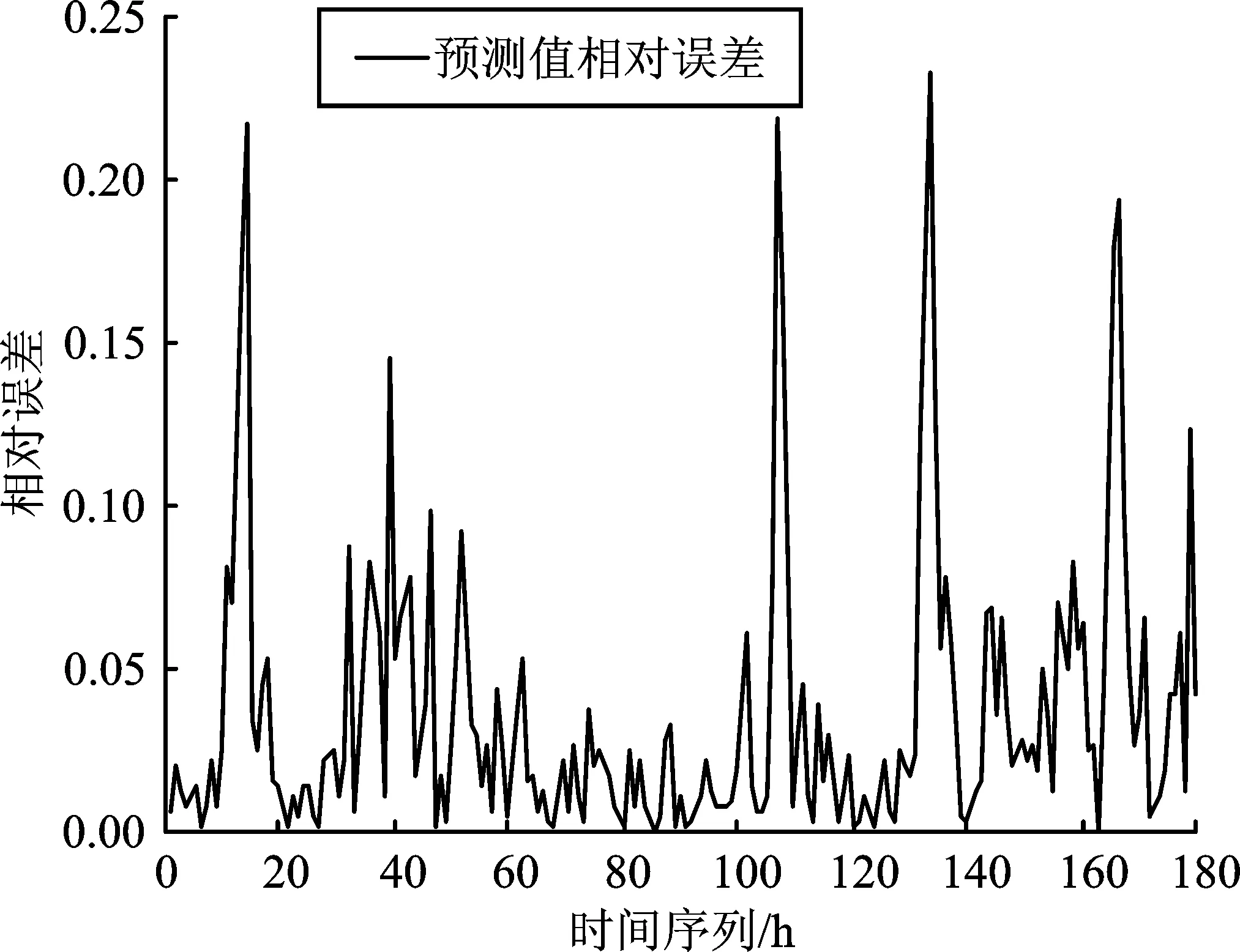
圖13 EEMD-ARIMA-GRNN模型算法相對誤差圖Figure 13.Relative error chart of EEMD-ARIMA-GRNN model algorithm

基于EEMD-ARIMA-GRNN混合模型算法的負荷預測的預測趨勢與實際數據大致相同。在突發外界因素條件的影響下，極值處的預測值與實際數據相差較小，相對誤差也控制在0.23以內，說明本文所設計的預測方法可同時兼顧電力負荷內在線性特征與非線性特征的特點，滿足負荷預測的精度要求。

通過4次仿真實驗得到4種預測算法的性能指標，如表1所示。

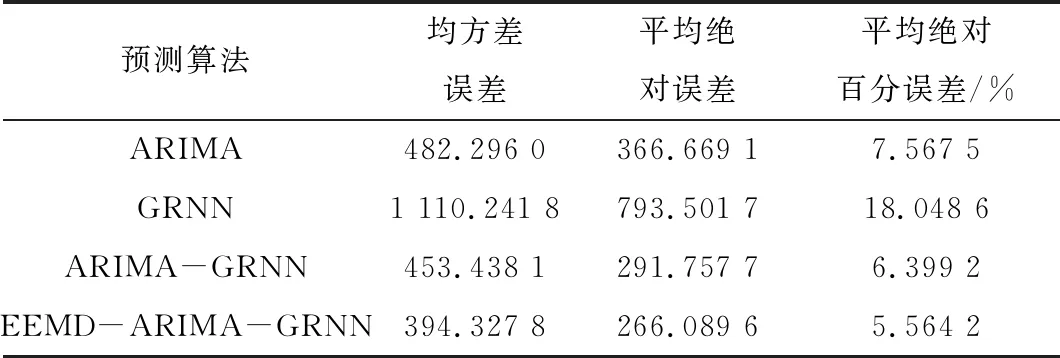
表1 性能指標表Table 1. Performance index

通過對表中數據進行分析，可知GRNN神經網絡算法效果最差，傳統ARIMA模型算法和ARIMA-GRNN算法的誤差值次之。本文所提出的EEMD-ARIMA-GRNN混合模型算法性能最佳，3項數據均比傳統ARIMA模型算法和GRNN模型算法更加優越。同時，對比4次仿真實驗相對誤差圖，可以清晰地看出混合模型算法的相對誤差在0.23之內，較大程度地提高了預測精度。綜上所述可知，相較于傳統單一算法，基于EEMD-ARIMA-GRNN混合模型的算法在電力負荷預測方面性能更優。

5 結束語

針對傳統負荷預測方法難以兼顧電力負荷內在的線性特征量與非線性特征量的問題，本文提出了一種基于EEMD和ARIMA-GRNN的混合負荷預測模型方法。仿真實驗證明，本文所提出的混合算法比傳統的時間序列算法和單一的神經網絡算法性能更加優越，能夠滿足短期負荷預測的要求。但是，本文所提方法并未考慮混合模型的計算開銷及工程應用實際需求，下一步研究中將對上述問題進行探討。