一種高功率因數無電解電容PMSM的設計與仿真

蔣凱文，金 海，許 參

(浙江理工大學 信息學院,浙江 杭州 310018)

近年來，隨著功率電子技術的快速發展，永磁同步電機(Permanent Magnet Synchronous Machine，PMSM)因其結構簡單、可靠性高、節能高效等優點得到了廣泛的應用。在永磁同步電機驅動系統中，電解電容位于變頻器的直流環節，并聯在直流母線兩端[1-2]。經電解電容濾波后，母線電壓雖然穩定，但是電壓值很高，使得整流二極管導通角變小，母線上的電流表現為脈沖波，畸變嚴重，電流諧波增加，降低了電網輸入的功率因數。因此，帶有電解電容的驅動電路還需增加功率因數校正(Power Factor Correction，PFC)電路[3-5]，才能降低對電網側的諧波影響。有電解電容永磁同步電機驅動拓撲如圖1所示。由于電機在實際應用環境中受高溫、高濕度、真空等因素影響，電容中成本高，體積大，電解液緩慢蒸發，影響電解電容壽命，降低了變頻驅動系統的穩定性。

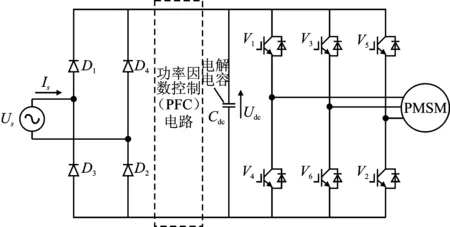
圖1 有電解電容永磁同步電機驅動拓撲Figure 1.Topology of PMSM drive with electrolytic capacitor

無電解電容驅動電路拓撲如圖2所示，其采用小容值的薄膜電容代替大容值的電解電容，薄膜電容體積小，輕便耐用，提高了電容器件的使用壽命。通過對功率的控制，無需PFC電路就可以提高電網輸入功率因數。目前，針對無電解電容逆變器驅動永磁同步電機系統的研究熱點為功率因數控制[6]。

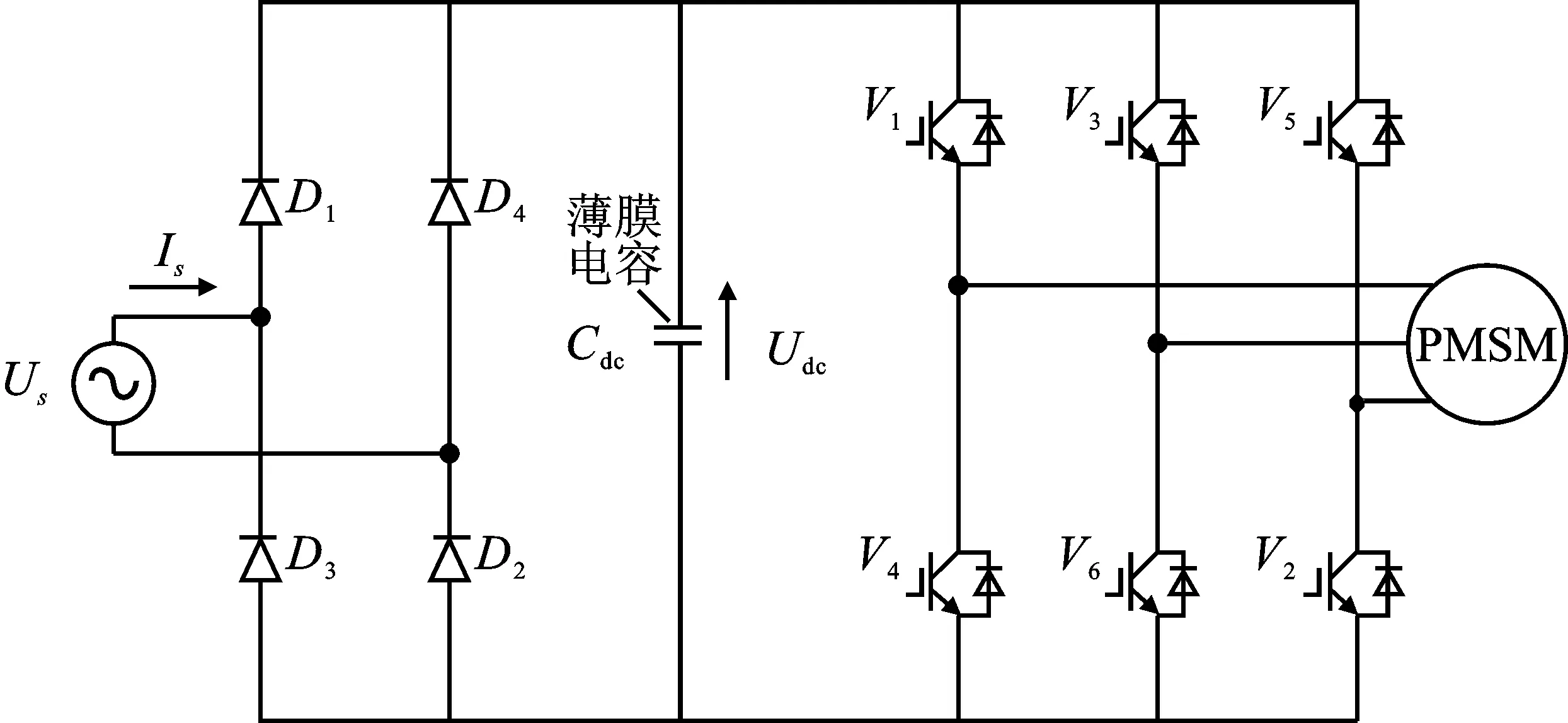
圖2 無電解電容永磁同步電機驅動拓撲Figure 2.Topology of PMSM drive without electrolytic capacitor

無電解電容逆變器技術最早由日本長崗技術大學的學者提出[7]。在風機、水泵等對電機動態響應不高但應用環境較復雜的領域，使用薄膜電容代替電解電容，提高了系統可靠性，延長了使用壽命。文獻[8]提出在矢量控制速度環和電流環之間加入1個功率環，利用PI控制器及重復控制器作為功率調節器。這種方法雖能較好地跟蹤正弦信號，但對控制器參數整定難度較高。文獻[9]基于功率平衡關系式和電壓約束方程提出精確功率控制法。該方法的應用建立在龐大的數據計算之上 ，d、q軸給定電流的選定依賴查表。

本文在無電解電容永磁同步電機矢量控制系統中，提出一種交軸相位補償結合直軸弱磁給定的控制策略，并在MATLAB/Simulink環境下搭建仿真模型。仿真結果顯示該控制策略可有效追蹤波動的給定電流，在功率因數控制和電網諧波抑制方面也有較好的效果。

1 PMSM矢量控制

1.1 坐標變換

永磁同步電機的轉子貼有永磁體，一般由鐵鈷鎳等材料構成，無需外加勵磁電路。永磁同步電機的定子裝有三相對稱繞組a、b、c，他們在空間上依次相差120°，如圖3所示。

圖3 各坐標軸之間關系Figure 3.Relationship between each axis

圖3中，由a、b、c3個軸線構成的坐標系是永磁同步電機三相靜止坐標系。a、b、c分別為定子三相繞組的軸線，3個坐標軸依次相差120°。由α、β構成的坐標系，稱為兩相靜止坐標系。α軸與三相靜止坐標系的a軸重合，β軸逆時針方向超前α軸90°，從三相靜止坐標系到兩相靜止坐標系的變換稱做Clark變換，變換方程如式(1)所示。

(1)

圖3中由d-q軸構成的坐標系稱為兩相旋轉坐標系，d軸成為直軸與轉子N極軸線重合，q軸為交軸逆時針方向超前α軸90°。d-q坐標系跟隨著轉子旋轉，圖中θ為轉子位置角，ω為轉子角速度，Ψf為轉子磁鏈，它的位置與d軸重合。從兩相靜止坐標系到兩相旋轉坐標系的變換稱作Park變化，變換方程如式(2)所示。

(2)

矢量控制的核心就是電流的解耦，永磁同步電機是一個非線性、強耦合的系統。矢量控制將定子三相電流矢量通過坐標變換，分解為相互正交的勵磁電流矢量iq和轉矩電流矢量id。這樣使永磁同步電機的控制方式類似于直流電機的控制方式，簡化了對電機的控制復雜程度[10-11]。

1.2 永磁同步電機數學模型

忽略電路飽和、鐵芯損耗以及電機中的渦流和磁滯損耗，永磁同步電機在d-q坐標軸上的電壓方程為[12]

(3)

轉矩方程為

(4)

式中，Te為電機輸出的電磁轉矩；ud和uq分別為定子電壓在d軸和q軸的分量；id和iq分別為定子電流在d軸和q軸的分量；Rs為定子電阻；Ld和Lq為定子電感在d軸和q軸分量，隱極電機Ld=Lq，本文選用凸極電機Ld≠Lq；pn是電機轉子的極對數；ωe是轉子旋轉電速度。

式(4)表示電機輸出電磁轉矩由電磁轉矩項3/2pniqΨf及磁阻轉矩項3/2pniqid(Ld-Lq)構成，磁阻轉矩項耦合程度較高。常見矢量控制中，取id=0，這樣輸出轉矩僅與iq有關。轉矩方程消除了耦合，簡化了對電機輸出轉矩的控制。

1.3 空間矢量脈寬調制

根據坐標變換，定子三相繞組電壓可以轉換為在矢量空間內以角速度ω旋轉的電壓矢量。三相逆變器的三組橋臂6種開關狀態在矢量空間內構成6組基本電壓矢量U1～U6，每條矢量之相隔60°，將矢量空間平均分成扇區Ⅰ～扇區Ⅵ，原理如圖4所示。

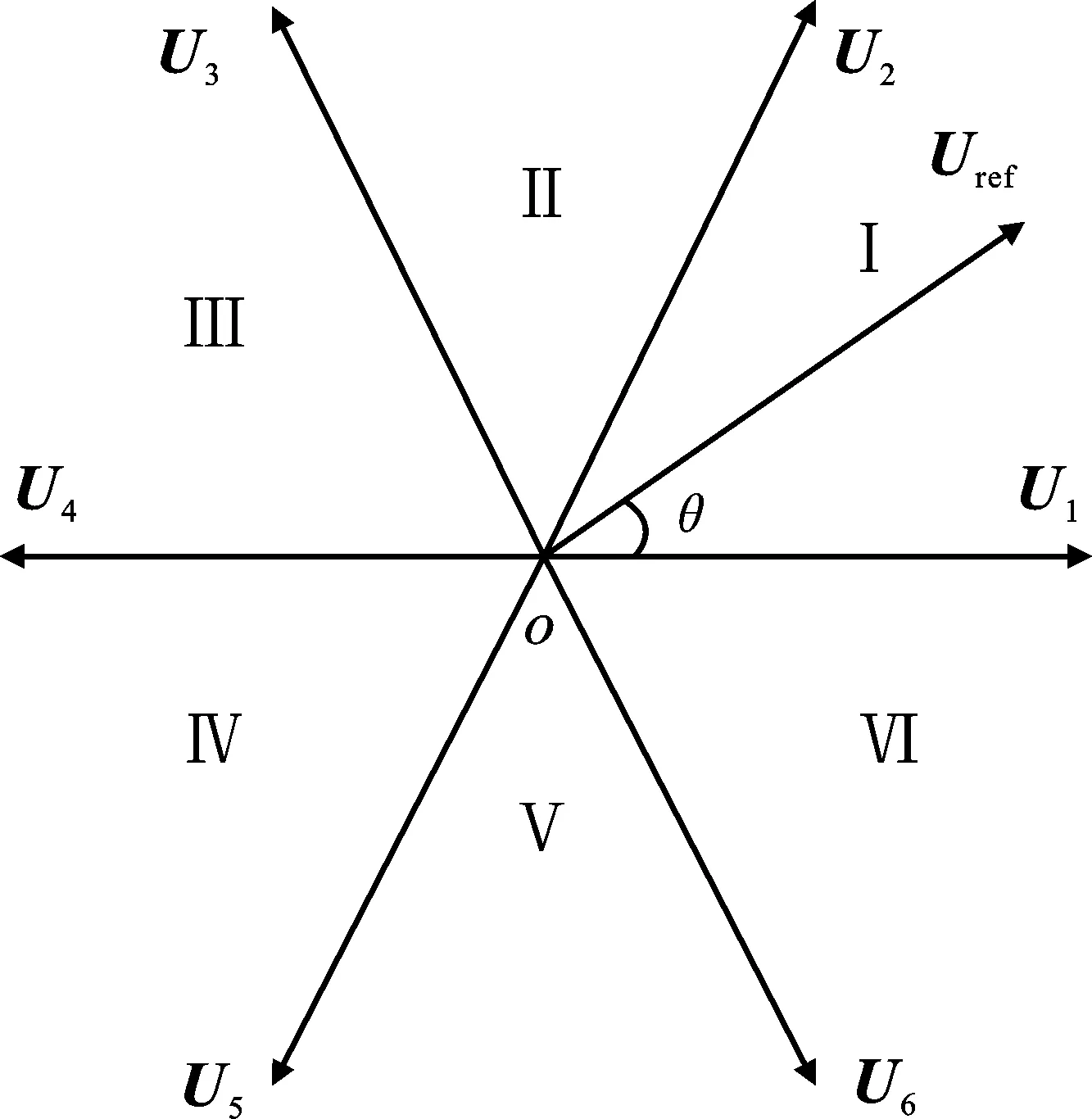
圖4 空間矢量脈寬調制原理圖Figure 4.Principle diagram of space vector pulse width modulatio

空間矢量脈寬調制(Space Vector Pulse Width Modulation，SVPWM)就是把某一時刻的電壓矢量Uref通過轉子位置角θ確定所在扇區，根據矢量疊加原理由該扇區鄰近的兩組基本電壓矢量和零矢量U0合成所得[13]。由于每組基本空間矢量都對應著逆變橋的一種開關狀態，故調整逆變橋的開關狀態和持續時間，便可在矢量空間中合成出近似于圓形的電壓矢量軌跡[14]。SVPWM開關損耗小，電壓利用率高，在交流電機矢量控制中廣泛應用于逆變模塊。

2 無電解電容逆變器PMSM矢量控制策略

2.1 功率因數

跟據定義，功率因數(Power Factor，PF)是有功功率p和視在功率s的比值[15]。在電機驅動系統中，受整流逆變等非線性環節影響，電網輸入的功率因數表示為

(5)

式中，φ為電網電壓與電流一次諧波的相位差；THD是總諧波畸變因數

(6)

式中，In是電網電流n次諧波的幅值。在永磁同步電機驅動系統中，高功率因數的控制就是要使電網電流與電壓同相，即控制φ=0。同時，降低電網電流高次諧波占比，使其波形接近正弦波形，即降低THD，從而達到對電壓波形的跟隨，實現高功率因數。

2.2 PMSM功率分析

假設電網電壓us是標準正弦波，且功率因數為1，即電網側電壓與電流同向，可以得到

(7)

其中，us、is為輸入電壓和電流；Us、Is是輸入電壓和電流的幅值；θs=ωst是輸入電壓的相角；ωs是輸入電壓的角頻率。由式(7)可以得到電網輸入功率

Ps=usis=UsIssin2(θs)

(8)

輸入電壓經全波整理后，由于用于濾波的薄膜電容很小，直流母線電壓udc隨輸入電壓二倍頻率波動。

udc=|Ussin(θs)|=Ussin(θs)·sgn(Ussin(θs))

(9)

綜合式(9)可以得到母線電容功率

(10)

式中，Cdc為母線電容值。

綜合永磁同步電機d-q坐標軸下電壓方程式(3)，可以得到逆變器輸出側功率

(11)

根據功率守恒原則，電網的輸入功率是輸出功率和逆變器輸出功率的和，即

Ps=Pdc+Pinv

(12)

薄膜電容充當母線電容時，Cdc值非常小，所以Ps≈Pinv，輸入功率近似等于輸出功率。合理控制逆變器輸出功率，即可調節電網側的輸入功率，達到調節功率因數的目的[16]。

2.3 q軸電流給定

忽略薄膜電容功率，將式(8)和式(11)帶入式(12)可得q軸電流給定為

iqref=iqavsin2(θs)

(13)

式中，iqav為q軸電流直流分量。由上式可知，與傳統的矢量控制相比，無電解電容控制中，母線點壓呈現二倍工頻波動。為了使電機的電流更好地跟隨母線電壓的波動，需要在電流給定中注入正弦量。

考慮薄膜電容對電流相位的影響，還需要在正弦注入量中加入相位修正。

薄膜電容屬于容性元件，電流流經電容后會與電壓產生逆時針超前90°的相位移。逆變器輸出電流由輸入電流與流經電容的電流疊加后形成，薄膜電容產生的電流相位移會導致輸出電流與輸入電壓形成相位差，q軸電流給定還需加入相位補償。根據電容充放電時的電流計算式，由電容造成相位超前角可表示為

(14)

加入相位補償后，q軸給定可表示為式(15)。

iqref=iqavsin(θs)sin(θs-θc)

(15)

2.4 d軸弱磁給定

當電機運行時，為了得到更好的解耦效果，一般d軸電流給定為0。當電機運行到較高轉速時，由于電機反電動勢與轉速成正比，反電動勢隨轉速上升。由式(3)可知，電機的電壓矢量變為負值，電機輸出轉矩不足，電機轉速下降，無法達到給定值，電機運行受逆變器電壓極限的制約。此時可在d軸給定一個小于零的電流，抵消永磁體磁場，降低電機反電動勢。這種在d軸給定去磁電流的控制稱作弱磁控制[17]。

無電解電容矢量控制由于母線電壓以二倍工頻波動，也須滿足電壓極限約束條件[18-19]。

(16)

為了實現高功率因數，d軸電流也是波動的。將電壓矢量方程帶入式(16)可得d軸電流給定

idref=idav+Asin(2θs)

(17)

式(17)中前一項為滿足電壓約束條件下的弱磁直流分量，后一項為波動分量。

本文在構建上述電流給定策略的基礎上，通過鎖相環來獲取電網電壓相位。鎖相環將外部輸入信號頻率與給定信號頻率進行比較，當二者頻率相等時進入鎖定狀態，輸出相位信息。本文將電壓信號輸入鎖相環，獲取波動相位θs。

3 仿真搭建與實驗結果分析

為了驗證本文提出控制策略的可行性，在MATLAB/Simulink環境下搭建永磁同步電機無電解電容控制系統模型。如圖5所示，仿真系統由永磁同步電機、母線電壓生成模塊、直軸弱磁給定模塊、交軸相位補償模塊、空間矢量脈寬調制模塊、逆變橋模塊、鎖相環模塊、坐標變換模塊、電流解耦模塊組成。電機參數為極對數pn=3，定子電阻Rs=0.685 Ω，電感Ld=7.5 mH，Lq=11.8 mH，定子磁鏈Ψf=0.125 Wb。輸入電壓為220 V頻率為50 Hz單相交流電，薄膜電容大小取20 μF。仿真系統給定轉速設置為2 400 r·min-1，負載轉矩為2 N·m。

圖5 無電解電容PMSM控制仿真圖Figure 5.Simulation diagram of PMSM control without electrolytic capacitor

圖6為無電解電容下電機負載運行時母線電壓的波形。從圖6可以看出，使用薄膜電容代替大容值的電解電容后，電容吸收電荷能力降低，母線電壓發生震蕩。

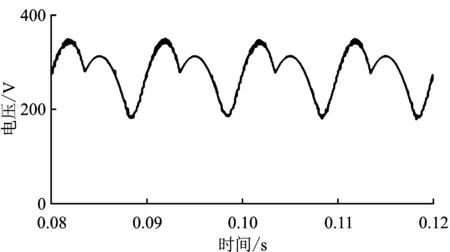
圖6 無電解電容下的母線電壓Figure 6.Bus voltage without electrolytic capacitor

圖7為電機空載運行時，q軸、d軸給定電流和實際電流的波形。無電解電容后，矢量控制下的解耦電流呈現正弦變化。在本文控制策略下，q軸、d軸電流給定隨母線電壓呈現二倍工頻波動，給定電流實現正弦化。合理設計d-q軸電流PI控制器，可實現q軸、d軸實際電流對給定電流的跟隨。

圖8為電機負載運行時母線電壓Udc、q軸、d軸給定電流和實際電流的波形。當進入穩態后，與空載運行相比，q軸和d軸給定電流隨母線點壓波動幅度增大，實際值也較好地跟隨了給定電流波動，相比空載時實際電流曲線更為平滑。圖7和圖8的結果表明，該仿真系統對于正弦條件下的給定電流具有較好的跟隨效果。

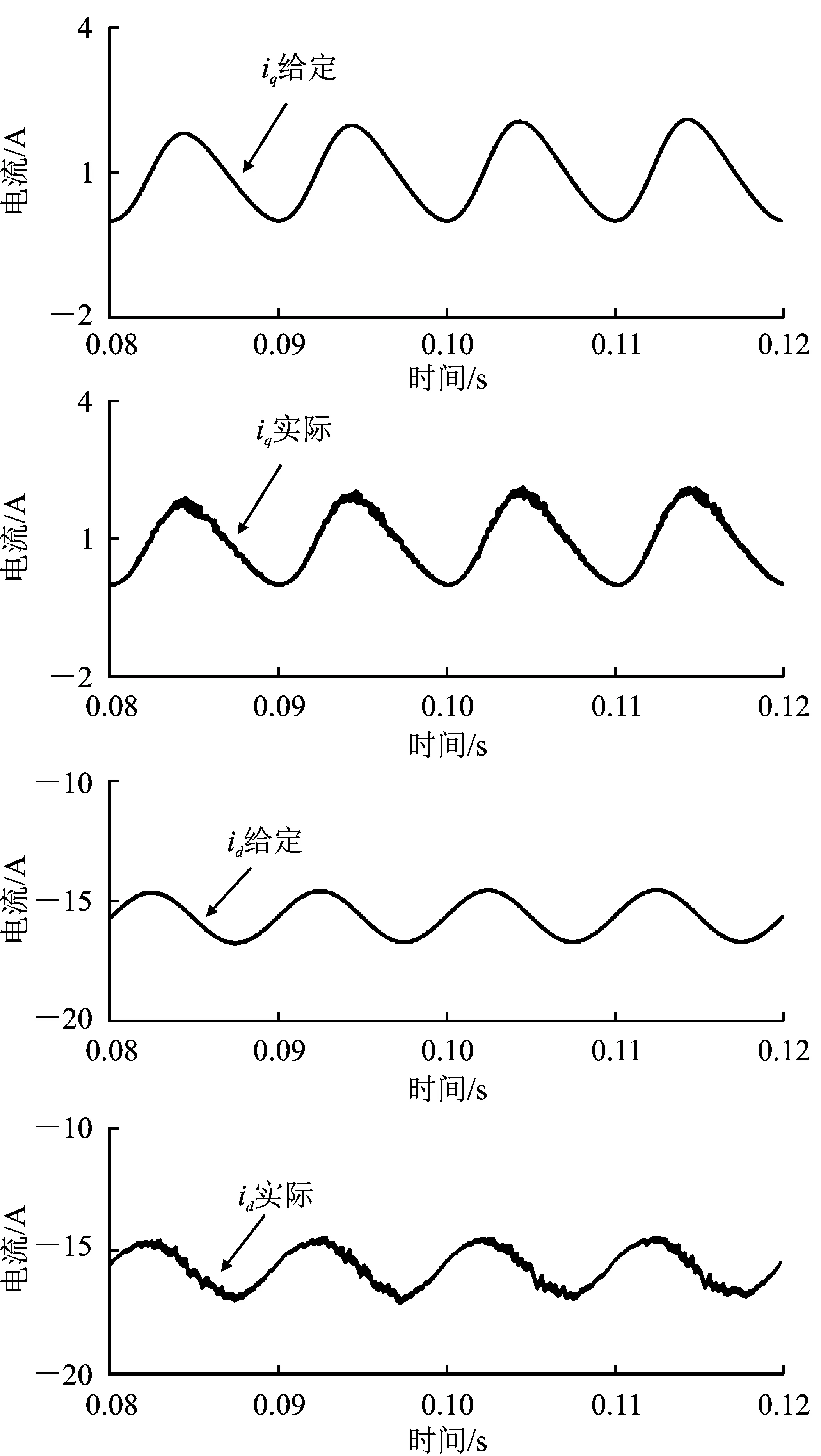
圖7 空載條件下電流跟隨效果Figure 7.Current tracking effect under no-load conditions

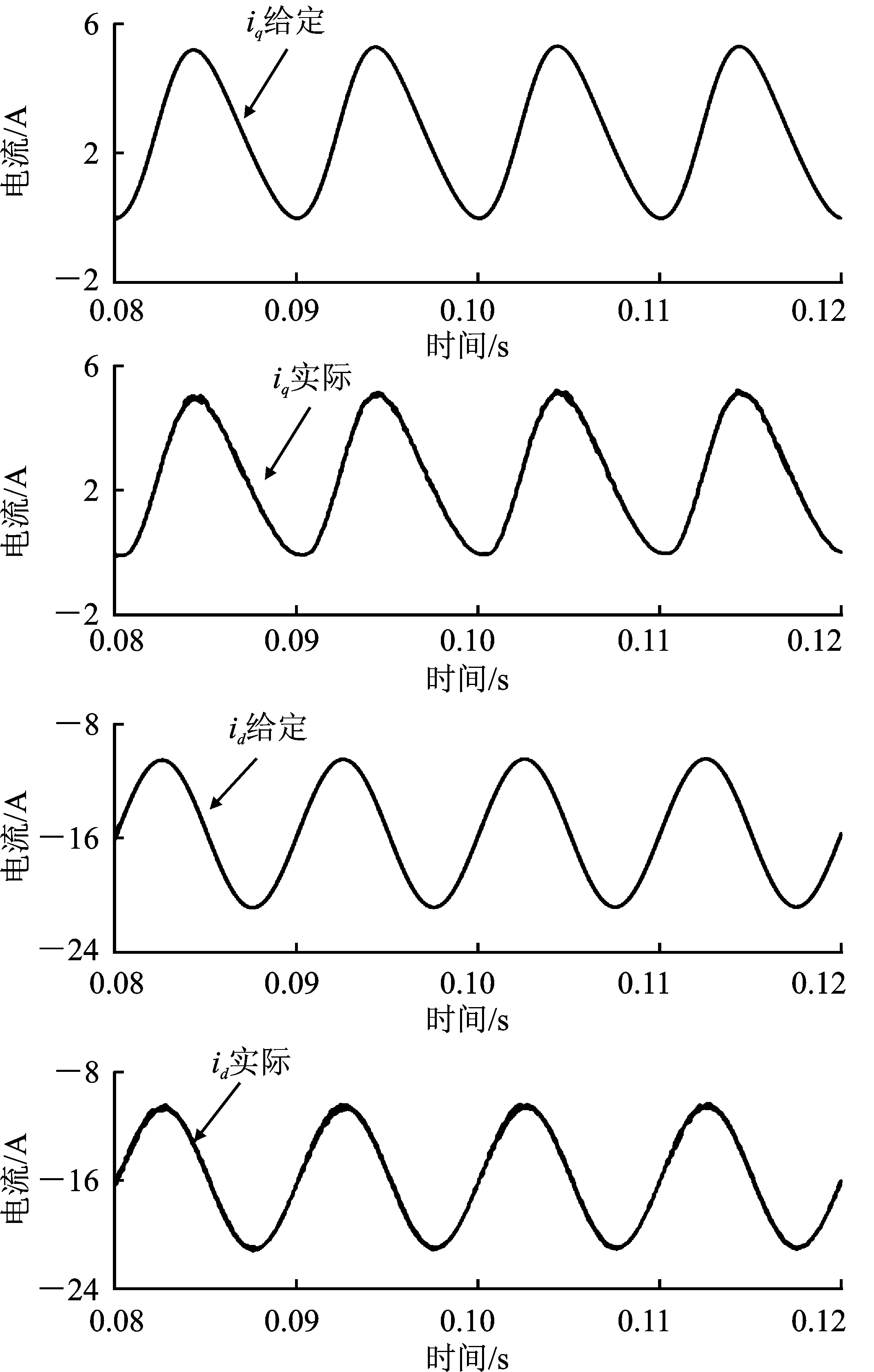
圖8 負載條件下電流跟隨效果Figure 8.Current tracking effect under load conditions

圖9為電機帶負載時傳統矢量控制下輸入電壓與輸入電流的波形圖。傳統控制下，輸入電流導通角較窄，波形畸變嚴重，電流與電壓之間存在相位差，功率因數較低。圖10為帶負載時本文提出的控制策略下的輸入電流與輸入電壓波形。與圖9相比，輸入電流導通角拓寬，加入相位補償與弱磁控制后，電流與電壓接近同相，電流畸變降低，電流與電壓波形跟隨程度提高。圖11為輸入電流波形快速傅里葉分析(Fast Fourier Transform，FFT)結果，由MATLAB/Simulink測算，THD為30.91%，根據式(5)可得，此時功率因數為93.51%。

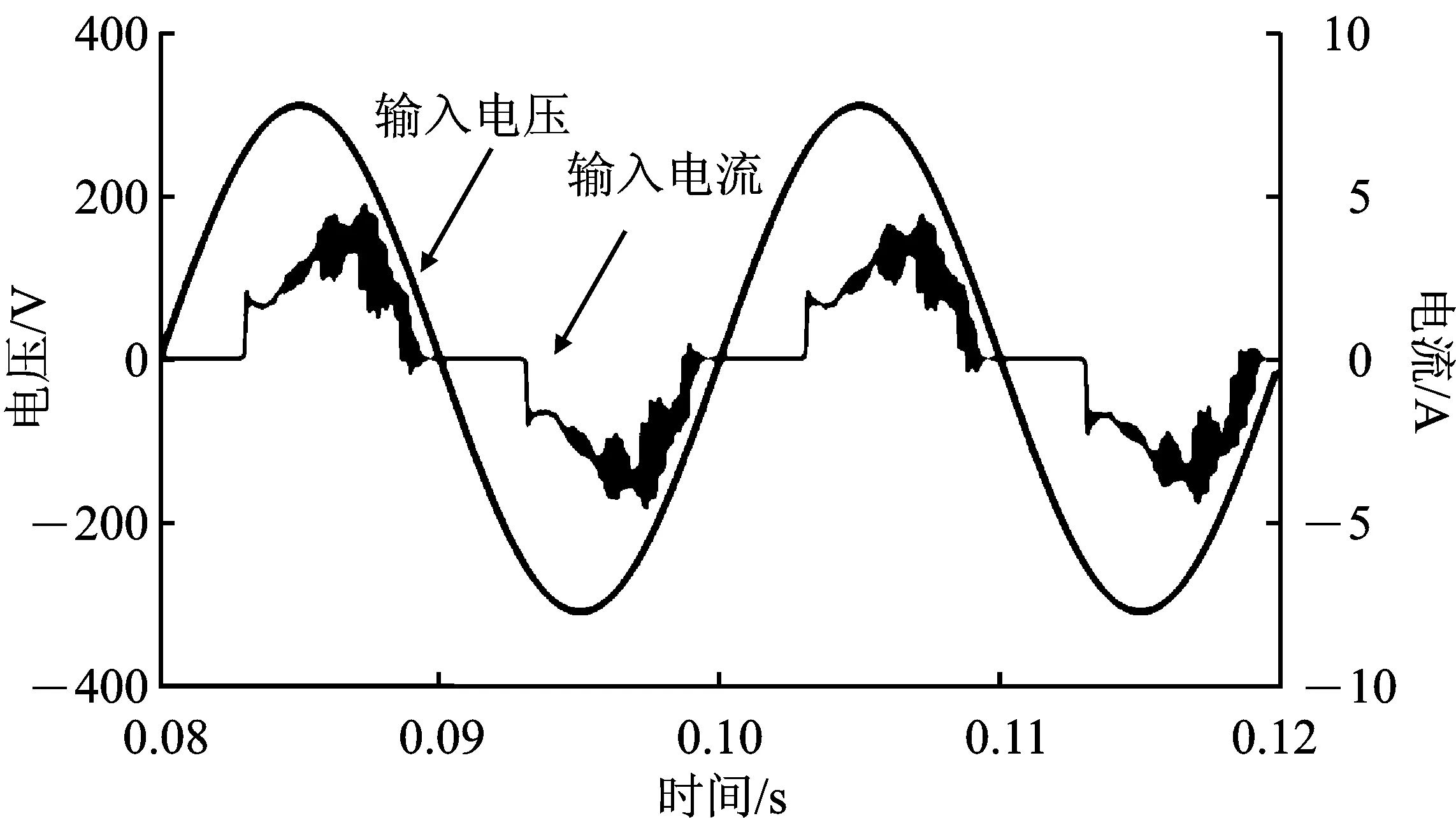
圖9 傳統矢量控制下的輸入電壓和輸入電流波形Figure 9.Input voltage and input current waveform under traditional field-oriented control

圖10 本文控制策略下的輸入電壓和輸入電流波形Figure 10.Input voltage and input current waveforms under the proposed control strategy

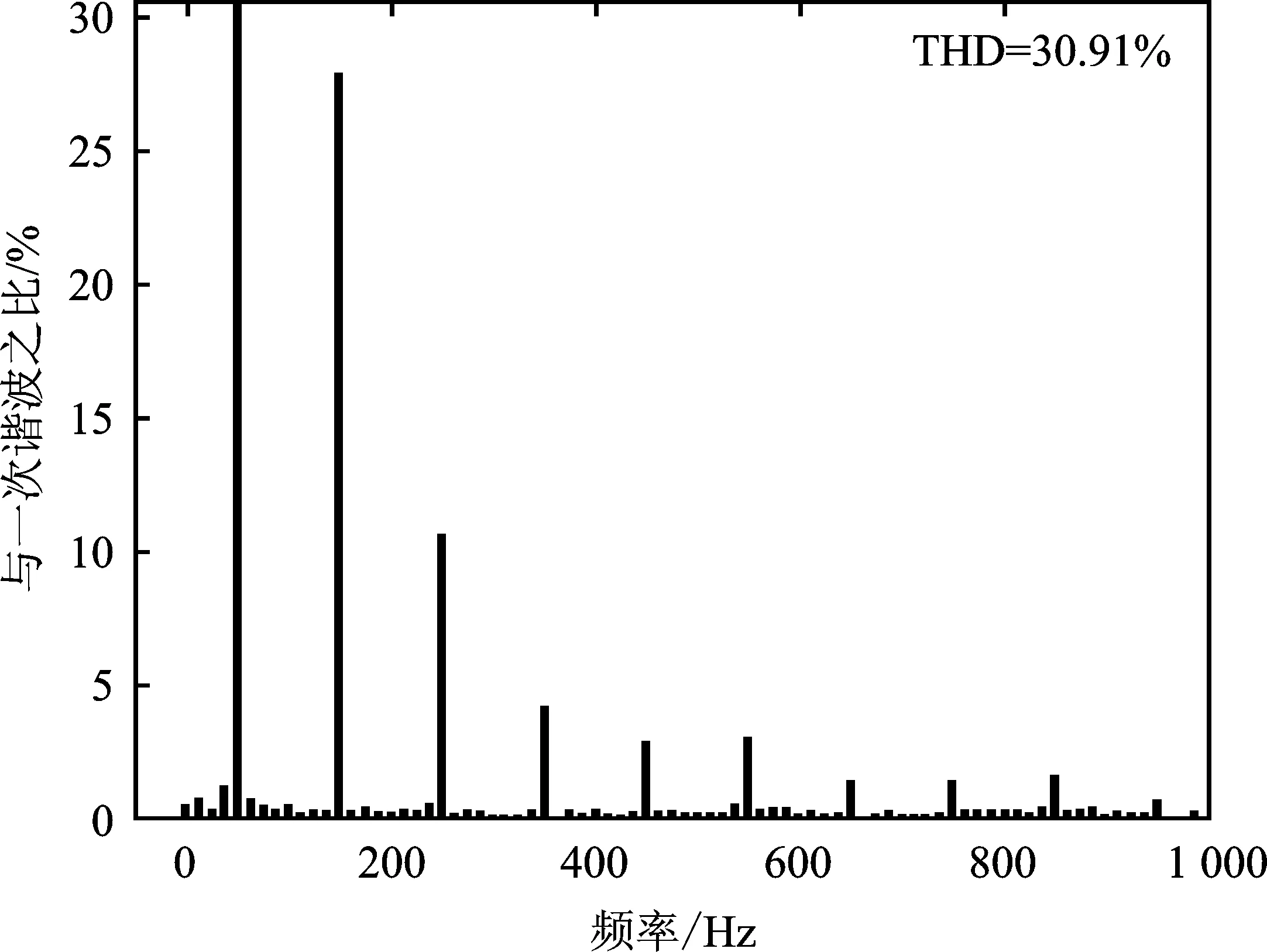
圖11 輸入電流波形FFT分析結果Figure 11.FFT analysis result of input current waveform

4 結束語

本文闡述了永磁同步電機數學模型和無電解電容控制原理，提出了一種結合交軸相位補償和直軸弱磁控制的永磁同步電機無電解電容控制策略，并在MATLAB/Simulink環境下搭建仿真模型進行仿真實驗。仿真結果表明，本文提出的控制策略可以有效抑制電網輸入電流畸變，提高電網功率因數。