例談基本不等式中的“3大注意”和“11個策略”
■河北南宮中學 溫世嫻 霍忠林
基本不等式常用來求函數最值(取值范圍)或證明不等式。高考中主要考查二元或三元基本不等式的應用。“一正、二定、三相等”是同學們耳熟能詳的使用基本不等式“口訣”。但是在解題過程中,部分同學對這“口訣”理解得不到位、對基本不等式的使用策略運用不當,從而導致得分不理想。鑒于此,本文總結了二元或三元基本不等式在使用過程中的“3大注意”和“11 個策略”,以期對同學們的學習提供幫助。
一、知識回顧
(1)若a∈R,b∈R,則a2+b2≥2ab(*),其中當且僅當a=b時,等號成立。

二、“口訣”的3大注意
(1)對“正”的理解:“一正”指的是數(代數式)必須均是正的,這是使用基本不等式的前提條件。比如,求函數y=x+的取值范圍時,顯然兩數不滿足“正”的條件,不能直接使用基本不等式,此時可以轉化為再使用基本不等式。因此,使用基本不等式之前應先看已知條件是否滿足“正”的條件。


(3)對“相等”的理解:判斷取等條件,必須在出現“定值”之后。在利用基本不等式求最值時,必須滿足“相等”的條件,若不滿足條件,則不能利用基本不等式求最值。比如,求的最小值時,采用≥2 來求最值是“行不通”的,原因就在于取等條件不滿足。但是在利用基本不等式證明不等式時,即使取等條件不滿足也可以使用。比如,當x>1時,證明:x2+。此時可以采用“x2+”來處理。
三、解題的11個策略
策略1 直接套用公式

策略2 添“項”湊“定值”
該策略指的是通過添加系數或添加常數來“湊”定值。

評析:本題通過添加系數2,從而湊出“和”為定值。

評析:本題通過添加常數項1,從而湊出“積”為定值。
策略3 乘“1”法
乘“1”法常分為“整體乘1”和“局部乘1”兩種形式。

評析:本題通過“整體乘1”策略,為基本不等式的使用提供了條件。實際上形如“已知x,y,z,r,s均為正數,且xa+yb=z,求的最小值”均可以采用此策略。

評析:本題通過“局部乘1”策略,為基本不等式的使用提供了條件。
策略4 換元法

評析:通過m=2x+y,n=y+1將本題轉化為策略3 來處理。一般情況,代數式中含有根式或含有一次式時可以考慮將根式或一次式進行換元,再求最值。
策略5 合理拆分
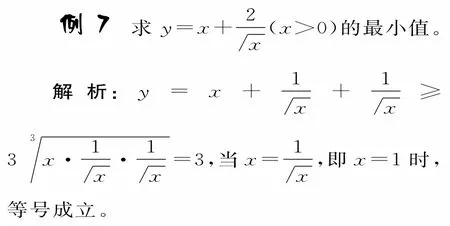
評析:注意到x=,因此將拆成相等的兩項,這樣可以保證了基本不等式“取等”的條件。“平均拆分”是合理拆分的最常見手段。
策略6 因式分解
該策略就是先對已知條件進行因式分解,再利用基本不等式解題。
例8已知a>0,b>0,且ab=a+b+3,求a+b的最小值。
解析:由ab=a+b+3,得(a-1)(b-1)=4。
所以a>1,b>1。
故a+b=(a-1)+(b-1)+2≥+2=6,當a-1=b-1,即a=b=3時等號成立。
所以a+b的最小值為6。
評析:一般形如“已知x,y,z,r,s均為正數,且ab=xa+yb+z,求ra+sb的最小值”可以考慮采用此策略。
策略7 連續多次使用基本不等式

評析:在多次使用基本不等式求最值時,必須保證等號同時成立。如果等號不同時成立,就無法使用基本不等式求最值。
策略8 主元思想

評析:在含有多個變量求最值時,可以考慮采用“主元思想,逐個擊破”策略,但是務必保證等號同時成立。
策略9 平方
該策略就是先將待求代數式平方,再應用基本不等式求解。

策略10 待定系數法

策略11 利用取等條件
利用基本不等式的“取等”條件來求最值或證明不等式,常用來處理“已知條件”和“問題”均是對稱式。
例13已知正實數a,b滿足a+b=2,求a3+b3的最小值。
解析:a3+1+1≥3a,b3+1+1≥3b,所以(a3+1+1)+(b3+1+1)≥3(a+b)=6,a3+b3≥2。
當a=b=1時等號成立。
所以a3+b3的最小值為2。
評析:注意到“題干”和“問題”均是關于a,b的對稱式,因此可以嘗試從a=b=1 條件來入手,通過a3+1+1≥3a,b3+1+1≥3b來順利實現解題的目的。
例14已知a>0,b>0,c>0,且a+b+c=1,求證:a2+b2+c2≥

綜上所述,基本不等式的學習中,要深入理解“一正、二定、三相等”這一條件。在解題過程中,要多整理、勤總結、善反思,只有這樣才能靈活掌握解題策略,實現精準備考。

