地下工程走廊寬高比對煙氣層溫度衰減系數影響研究

毛 維 邢哲理 金曉公 李超峰 侯普民 李 娟

（軍事科學院國防工程研究院 北京 100036）

0 引言

火災煙氣熱特性一直是火災研究的焦點，高溫煙氣不僅可以直接對人員產生熱灼傷[1,2]，還會嚴重影響建筑結構強度[3]，建筑內溫感報警器和自動噴水滅火系統由頂棚附近的熱煙氣觸發，煙氣層溫度的衰減程度是影響人員疏散的重要因素。地下工程處于地下，空間相對封閉并且與外界連通受限，火災時煙氣熱特性與地面建筑存在差異，人員疏散逃生和消防救援的復雜性及危險性遠大于地面建筑[4]。

單室—走廊是地下工程的典型結構，單室和走廊是構成地下工程的基本元素，工程內單室發生火災時，人員通過走廊向外逃生。前人針對單室[5,6]和巷道（隧道）[7-9]內的溫度預測模型進行了很多研究，針對地下工程典型單室—走廊結構的煙氣熱特性研究相對較少。因此，本文基于相似原理搭建了地下工程一個防火分區的單室—走廊結構模型實驗臺，構建了數據采集系統，通過改變火源規模和走廊尺寸進行了10 個工況的火災模型實驗，將模型實驗結果和前人理論模型預測結果進行了對比分析，以期得到地下工程火災時走廊高寬比對煙氣層溫度衰減系數的影響。

1 理論模型

一般情況下，地下工程的單室內發生火災時，煙氣會通過門流入走廊，在走廊進行擴散，擴散過程中熱煙氣與冷空氣相互卷吸，熱煙氣通過對流和輻射與圍護結構進行換熱，因此煙氣溫度在擴散過程中會逐漸衰減。胡隆華[10]基于雙區域理論、連續性方程及能量方程推導得到了火災煙氣溫度在隧道長度方向的衰減模型，如式（1）所示，其中煙氣層溫度衰減系數為。

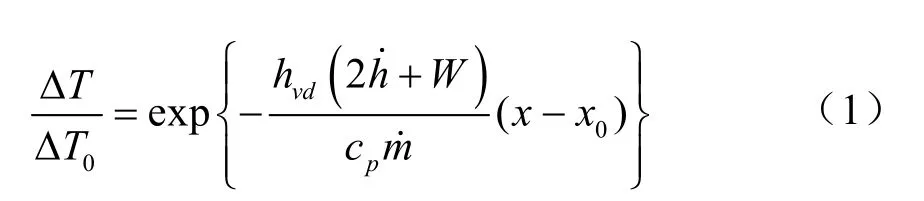
Li 等人[11]基于質量和能量守恒推導得到了隧道內煙氣溫度在長度方向簡化的一維衰減模型，如式（2）所示，其中煙氣層溫度衰減系數為簡化的模型可以快捷的預測煙氣溫度，其在推導過程中忽略了熱煙氣對冷空氣的卷吸作用。

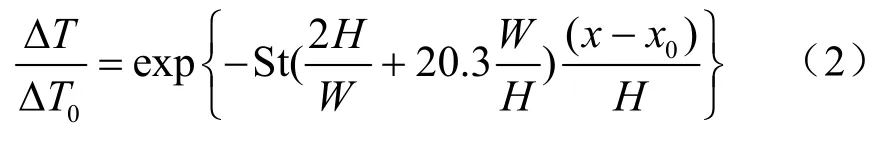
筆者[12]基于雙區域模型、連續性方程以及能量方程，針對地下工程單室火災時長走廊中的煙氣層溫度衰減模型進行理論推導，得到一種走廊內煙氣層溫度預測模型，如式（3）所示，其中煙氣層溫度衰減系數為。

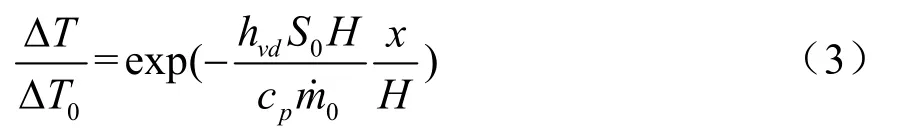
式（1）～（3）中，H為走廊高度，m；W為走廊寬度，m；x為距離，m；為煙氣層厚度，m；hvd為有效換熱系數，c p為定壓比熱，kJ/(kg·K)；為煙氣流量，kg/s；ΔT為煙氣層溫度與冷空氣溫度差，K；下角標0 表示物理量的初始值。

2 實驗

2.1 實驗臺搭建

本文以某地下工程的一個防火分區為研究對象，該對象為單室-走廊結構，火源位于單室內，火災發生后煙氣由單室蔓延至走廊，通過走廊擴散至口部。考慮到全尺寸實驗的危險性和難以重復性，本文根據相似理論和關鍵相似準則[13]通過搭建模型與實體為1:4 的模型進行實驗研究。模型實驗臺火源單室的尺寸為1.2m×0.75m×0.6m，單室門尺寸0.75m×0.2m，走廊長為15 m，走廊寬度和高度尺寸根據不同工況設置。實驗模型主要采用塑鋼材料，通過模塊化連接可以改變模型走廊的寬度和高度尺寸，火源房間主要采用耐高溫鋼化玻璃，各模塊采用防火密封劑進行封堵密封。基于模型率分析得到模型與實體之間的溫度關系為1:1，熱值比例為1:64，火源功率比例為1:32，時間比例為1:2。

2.2 工況設置

模型實驗綜合考慮到不同火源規模和不同走廊尺寸的工況，采用三種不同直徑的圓形油池火作為火源（燃料為正庚烷），并結合走廊寬度和高度的變化共進行了10 個工況的模型實驗，如表1 所示。

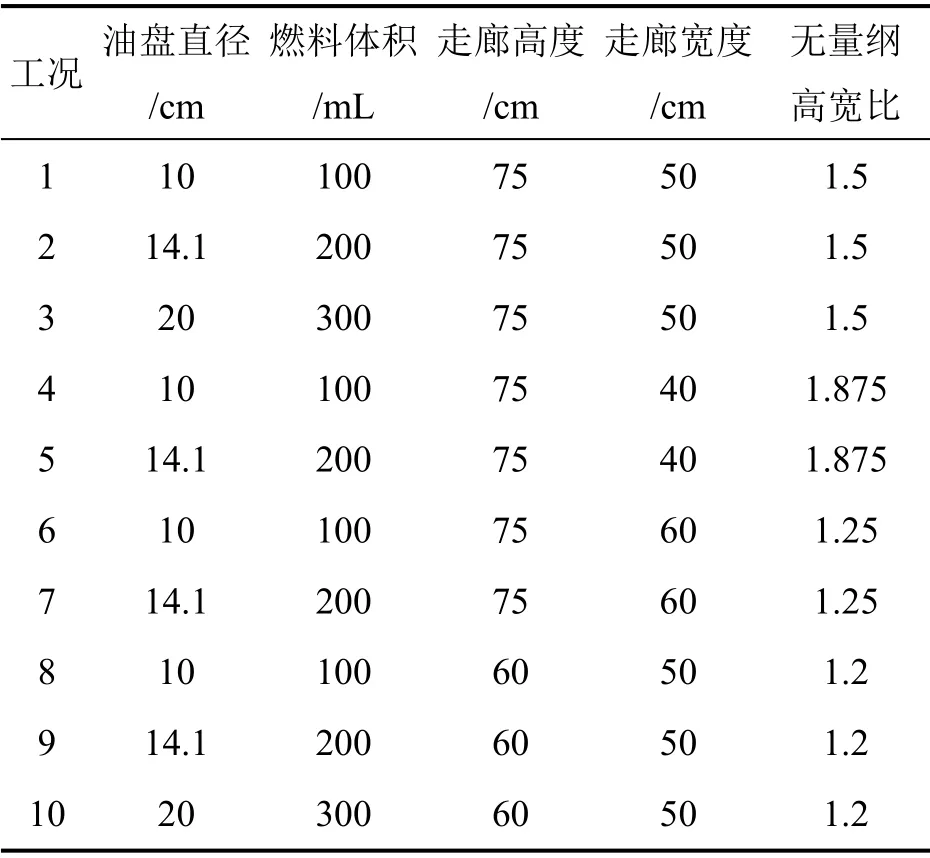
表1 實驗工況Table 1 Experimental conditions

2.3 實驗臺測點布置

實驗臺中共設置了8 組熱電偶樹（T1～T8），如圖1 所示。單室中（T1～T3）每組熱電偶樹豎直方向上有8 個熱電偶探頭，從下到上依次為1#～8#探頭，相鄰的兩個探頭相距8cm，1#探頭與地面、8#探頭與屋頂距離都為2 cm；工況1～7 時走廊中（T4～T8）每組熱電偶樹有6 個熱電偶探頭，與頂棚之間距離由上至下分別為1、15、29、43、57、71cm，工況8～工況10 時走廊中每組熱電偶樹有5個探頭，與頂棚之間距離由上至下分別為1、15、29、43、57cm。實驗過程中溫度數據采集系統將各測點處溫度實時顯示和存儲在電腦上，數據采集間隔為5s。

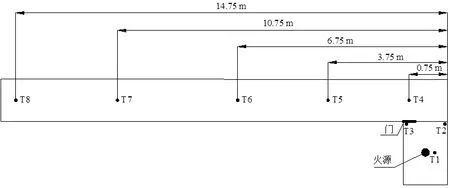
圖1 模型實驗測點布置圖Fig.1 Layout of measuring points in model experiment

2.4 實驗過程

為保證安全順利地展開模型實驗，主要分三個階段進行：

（1）實驗準備階段：檢查實驗臺是否完好；檢查實驗數據采集系統是否正常；檢查其他儀器和輔助設備是否正常工作。這一階段工作的目的是確保客觀條件能夠保證實驗正常進行。

（2）實驗進行階段：記錄環境溫度、實驗時間以及實驗工況等數據；開啟實驗數據采集系統、點火并記錄實驗數據；實驗結束后停止采集數據，通過通風排煙將實驗臺冷卻恢復至環境條件。

（3）實驗后工作階段：查看燃料是否燃盡；保存實驗數據。

3 結果與討論

3.1 煙氣層溫度隨距離的變化規律

從前人的研究來看，煙氣層溫度隨著與火源距離的增大，呈指數衰減規律，對于模型實驗結果與前人研究得到的規律是否具有一致性需要將模型實驗結果進行計算分析。考慮將不同火源規模條件下的模型實驗結果進行分類對比分析，圖2～4 分別為油池直徑10cm（工況1、4、6、8）、油池直徑14.1cm（工況2、5、7、9）和油池直徑20cm（工況3、10）時模型實驗煙氣層溫度隨距離的變化規律。從圖2～4 中可以看出，筆者將10 個工況條件下得到的煙氣層溫度均隨無量綱距離變化進行了擬合，圖中的曲線為擬合曲線，觀察發現實驗得到的結果與前人得到的理論模型具有規律一致性，均呈指數衰減規律。通過對實驗結果的曲線擬合可以得到實驗結果的煙氣層溫度衰減系數，進而可以與理論結果進行對比分析，研究無量綱寬高對衰減系數的影響及相關理論模型對于地下工程火災的適用性。

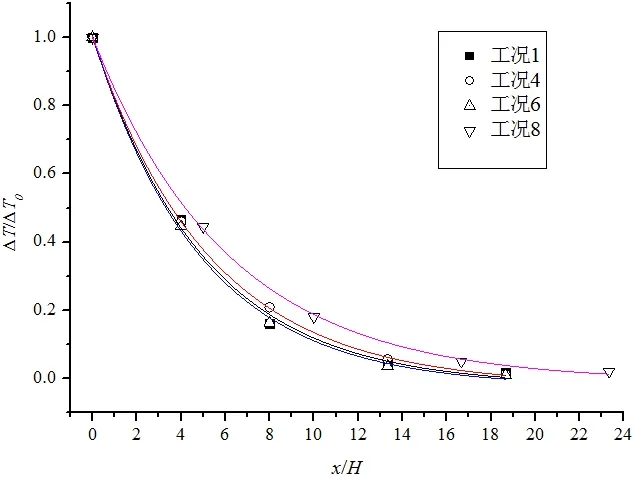
圖2 油池直徑為0.1m 時煙氣層溫度衰減規律Fig.2 The smoke temperature attenuation law when diameter is 0.1m

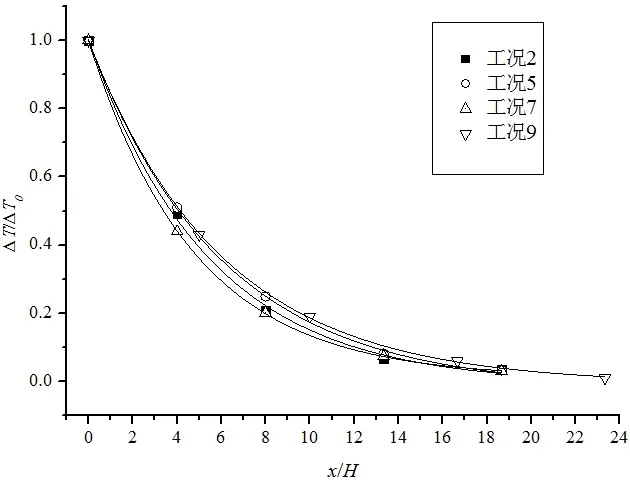
圖3 油池直徑為0.14m 時煙氣層溫度衰減規律Fig.3 The smoke temperature attenuation law when diameter is 0.14m

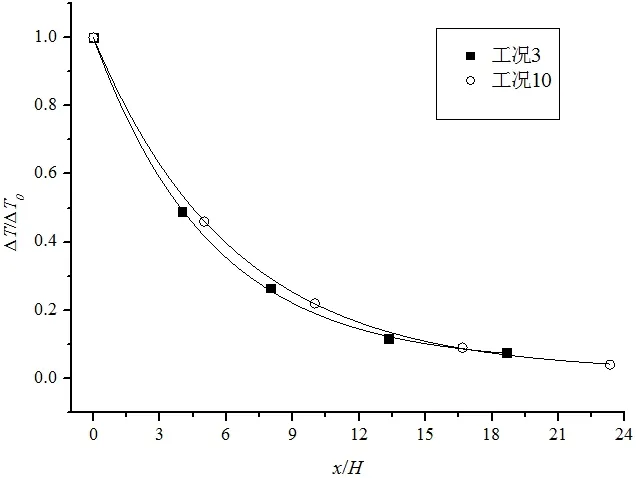
圖4 油池直徑為0.2m 時煙氣層溫度衰減規律Fig.4 The smoke temperature attenuation law when diameter is 0.2m

3.2 衰減系數預測值與實驗值對比

為了便于對比分析衰減系數預測值與實驗值，定義γ為模型實驗得到的溫度衰減系數和預測模型的衰減系數之間的相對誤差，γ可表示為：其中km為模型實驗結果擬合得到的衰減系數，m-1。模型實驗得到的溫度縱向衰減系數和預測模型衰減系數以及它們之間的相對誤差如表2 所示。從表中可以發現，式（1）和式（3）得到的衰減系數與模型實驗得到的衰減系數之間的誤差在10%以內，式（2）在高寬比為1.2 時預測效果良好。通過表中數據對比還可發現衰減系數隨火源規模的增大呈減小趨勢，即火源規模越大，走廊中煙氣層溫度衰減越小。

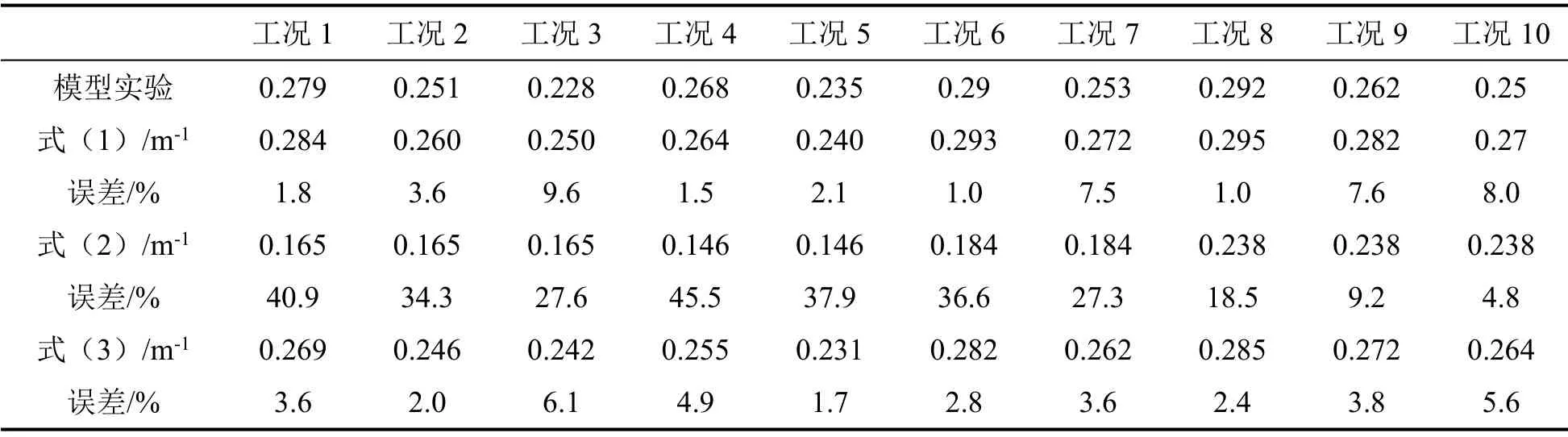
表2 模型實驗和預測模型衰減系數及相對誤差Table 2 Attenuation coefficient and relative error of model experiment and prediction model

3.3 走廊高寬比對煙氣層溫度衰減系數影響

定義走廊中無量綱高寬比為H*=H/W。圖5～圖7 所示為不同火源規模條件下（油池直徑：0.1m，0.141m，0.2m），衰減系數隨走廊無量綱高寬比的變化。從圖中可以發現，在同一火源規模條件下，煙氣層溫度的衰減系數隨走廊無量綱高寬比的減小而增大，這說明無量綱高寬比減小使得熱煙氣向圍護結構的散熱量相對增加，卷吸作用導致的熱損失就相對減少，這個結果與Lee 等人[14]得到的結論類似。由于式（2）忽略了卷吸作用，因此它與模型實驗和另兩個預測模型之間差值可以一定程度上反映卷吸作用導致的煙氣熱損失情況。從表2 中可以發現，式（2）的預測結果與另兩個模型及模型實驗結果之間的差別隨著高寬比的增大而減小，這亦證明了上述結果。因此，可以推斷，當走廊的高寬比小到一定值以后，Li 等人得到的預測模型也可以較好地預測實驗結果。實際上在工況9 和10時，走廊的高寬比為1.2，式（2）與模型實驗之間衰減系數的相對誤差在10%以內，預測結果與實驗結果基本一致。

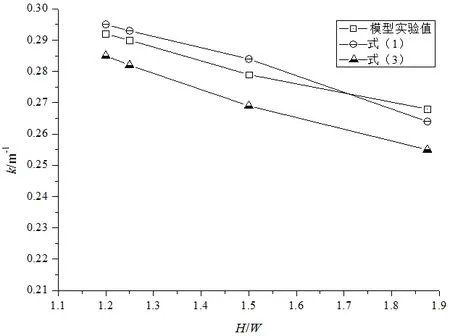
圖5 油池直徑為0.1m 時衰減系數變化Fig.5 The attenuation coefficient changes when diameteris 0.1m

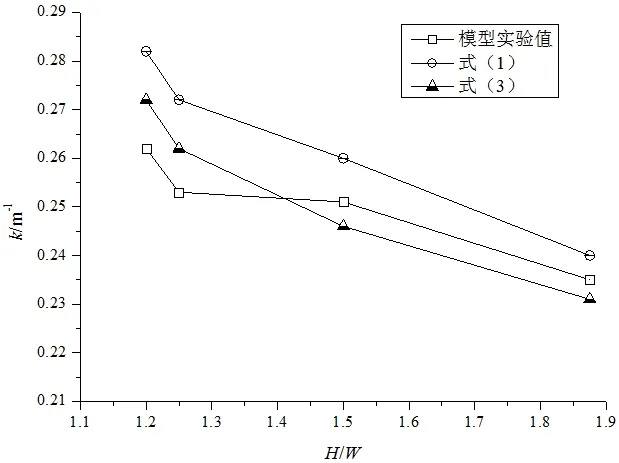
圖6 油池直徑為0.14m 時衰減系數變化Fig.6 The attenuation coefficient changes when diameteris 0.14m

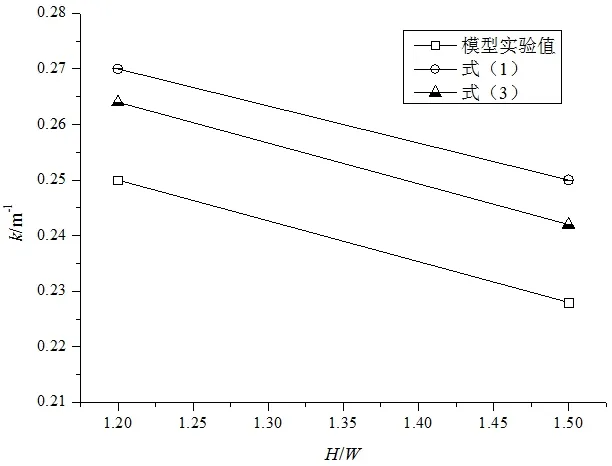
圖7 油池直徑為0.2m 時衰減系數隨走廊高寬比變化Fig.7 The attenuation coefficient changes when diameter is 0.2m

4 結論

基于以上模型實驗結果和理論模型預測結果的分析，可以得到地下工程走廊煙氣層溫度的衰減系數隨著走廊高寬比的減小而增大，煙氣與圍護結構之間的換熱相對增強，煙氣與空氣之間的卷吸換熱作用相對減弱，衰減系數隨火源規模的變大呈衰減趨勢，火源規模越大走廊中煙氣層溫度衰減越小。