關于β-凸函數若干性質的探討
劉和英
(合肥科技職業學院 基礎部,合肥 230000)
上世紀60年代中期誕生了一門新的數學分支——凸分析,它以凸集和凸函數為基本研究對象,在純粹數學與應用數學的眾多領域具有廣泛的作用。但是凸分析的局限性也很明顯, 實際問題中的大量函數是非凸的, 因此,人們從多種途徑推廣了凸函數的定義, 提出了許多廣義凸性的概念和理論, 現在已經成為數學規劃論和最優化理論等重要的理論基礎和有力工具。1978年,Breckoner[1]給出了S-凸函數的概念, Hudzik等[2]中得出了S-凸函數的若干重要性質。顯然,當S=1時,S-凸函數就是我們通常的凸函數。1985年Godunova等[3]首先給出了 Godunova-Levin 函數的定義,我們容易知道非負單調函數和非負凸函數都是它的一種特殊情況。1995年,Dragomir等[4]定義并探討了P-函數。通過對以上S-凸函數、Godunova-Levin函數、P-函數等這些函數的研究,2007年Varo?anec[5]得到了一種統一的新函數類, 稱為h- 凸函數, 并且探討了h- 凸函數的許多重要性質。受到[5]的啟發, 我們主要研究了一般實線性空間中β- 凸集, 以及在它上面定義的β-凸函數,顯然從定義可以看出β-凸函數是與h- 凸函數不同的一種凸函數,因此我們可以考慮將h-凸函數的一些性質推廣到β-凸函數。
定義1 如果對任意的x,y∈K, 對任意的λ,μ∈[0,1]且λβ+μβ=1, 其中,0 < β ≤ 1,有λx+μy∈K, 則稱K為β- 凸集。特別地,當 β= 1時,K為凸集。
定義2 設E是實線性空間,K?E,若M是包含K的最小的β- 凸集,則稱M 是K的β- 凸包,記作M=convβK。令(xn)n∈N是K 中的任意點列,則有:
定義3 設E是實線性空間,K是E中的β- 凸集, 如果對任意的x,y∈K,對任意的λ,μ∈[0,1]且λβ+μβ=1, 其中0 <β≤ 1。都有:f(λx+μy)≤λf(x)+μf(y)。
則稱f是β-凸函數。特別地, 當β= 1時,f為凸函數。
1 主要結果
定理1 設E是實線性空間,K是E中的β- 凸集,f是K上的β-凸函數且f(0)=0。若對任意的x,y∈K, 對任意的λ,μ∈[0,1],使得λβ+μβ≤1 其中0<β≤1,都有:
f(λx+μy)≤λf(x)+μf(y)。
證明:對任意的x,y∈K, 對任意的λ,μ∈[0,1],當λβ+μβ=1時顯然成立。
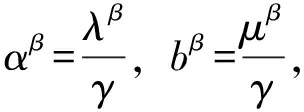
顯然a,b∈[0,1]且aβ+bβ=1,因此我們有:
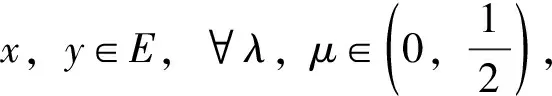
使得λβ+μβ≤1 其中0<β≤1,都有f(λx+μy)≤λf(x)+μf(y) ,則f(0)=0。
證明:不妨設f(0)≠0,則有f(0)>0。令x=y=0,從而有:
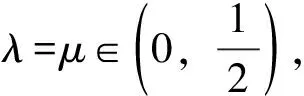
定理 2 設E是實線性空間,K是E中的有限子集。若M=convβK,且f是M上的β-凸函數,則有supf(M)=maxf(K)。
證明:我們令:
根據f的β-凸性,可得:
因此,根據定義2我們有:
從而有 supf(M)=maxf(K) 成立。
定 理 3 設E是實線性空間,f是E上的β-凸函數,
我們令ω1,ω2,…,ωn∈[0,1]與x1,x2,…,xn∈E。

證明:當n=2時,我們不妨設:
從而有λβ+μβ=1,顯然不等式成立。假設 n-1 時不等式亦成立,下面來證明對(ω1,ω2,…,ωn)與(x1,x2,…,xn)的凸組合不等式仍然成立。我們有:
注:顯然當 β= 1時, 此不等式就是凸函數的典型的Jensen-型不等式。在文[6]中的Godunova-Levin 函數得到了與此類似的結果。下面令K是有限非空的正整數集合,我們定義一個指標集的函數F如下:
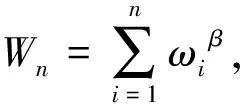
推論2 設E是實線性空間,f是E上的β-凸函數,若M,K是有限非空的正整數集,且M∩K=?,則對?ωi>0,xi∈E(i∈M∪K),都有F(M∪K)≤F(M)+F(K)。
證明:我們令:
不妨設:
顯然滿足λβ+μβ=1, 又由f是E上的β-凸函數,可得:
因此,我們有下面的不等式:
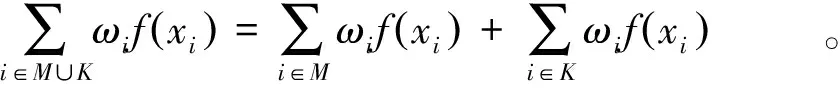
可得:
顯然對?ωi>0,xi∈E(i∈M∪K),都有F(M∪K)≤F(M)+F(K)成立。

