非中心入射流旋轉圓盤水躍現象的實驗與模擬

任思遠，劉春江，2，郭凱，劉輝，項文雨，謝春剛，李雪

（1 天津大學化工學院，天津 300072；2 天津大學化學工程聯合國家重點實驗室，天津 300072；3 自然資源部天津海水淡化與綜合利用研究所，天津 300192）

由于旋轉圓盤表面的液膜具有較高的傳熱和傳質效率，入射流旋轉圓盤在許多工程中得到廣泛應用，如微電子制造、食品加工和航天航空工業[1]。當垂直入射的液體撞擊旋轉圓盤表面時，液體在離心力、慣性力和黏性力的共同作用下，在圓盤表面沿徑向和切向方向流動，此時進口部分會出現液膜較薄的區域，在臨界半徑處液膜厚度會迅速增加，形成水躍[2]。水躍會影響旋轉圓盤表面上的液膜分布，進而影響到圓盤表面傳熱、傳質和反應過程，因此水躍引起研究人員的廣泛關注。Rayleigh[3]首先提出了無黏流體在靜止固體表面上的水躍模型。此后，Watson[4]研究了入射流在靜止表面上的層流和湍流流動，闡明了液體黏度對水躍半徑的影響。Bush等[5]在Watson的基礎上研究了表面張力對入射流水躍現象的影響，提出的理論模型與實驗結果具有更好的一致性。當固體表面開始旋轉后，研究工作大部分集中于旋轉圓盤表面的液膜厚度及流動形態，對進口區域水躍現象研究較少。Thomas 等[6-7]對旋轉圓盤表面的水力學現象進行了分析，預測隨著圓盤轉速的增加，液膜逐漸變薄，當轉速增加到一定的速度時，水躍現象將會消失，并劃分了三個不同的流動區域：內部慣性主導區、過渡區和外部旋轉主導區。Buyevich等[8]對入射流撞擊平面形成的水躍現象進行了數值模擬，他們將進口部分劃分為五個區域：入射區域、液膜黏性邊界層出現前后的層流區域、水躍區域和亞臨界區域。Avedisian等[9]利用高速照相系統研究了不同重力情況下的水躍現象，發現在微重力情況下，水躍直徑比在正常重力情況下大。Ozar等[10]利用激光界面反射技術測量了液膜厚度沿圓盤半徑的瞬時分布，驗證了Thomas等提出的理論。Duchesne 等[11]發現對于相同的表面，當進口高度一定時，Fr數不會隨著黏度和表面張力的變化而變化。Mohajer 等[12]的實驗驗證了Duchesne 的理論，但是發現表面張力的變化會影響Fr數。Wang 等[13]對旋轉圓盤表面的進口部分從停滯區、發展的層流邊界區、完全湍流區和水躍區四個方面展開研究，分析了旋轉對水躍的影響。之后Wang等[14]利用激光多普勒測速儀測定了甘油-水體系在旋轉圓盤表面形成的液膜的速度分布，并利用VOF 模型進行了數值模擬，發現水躍通常在低轉速、高黏度和入口直徑偏小的情況下出現。同時入口直徑決定是否有水躍現象的出現，但是對水躍半徑的影響很小。

上述對水躍的研究均為進口為圓盤中心的情況下進行的實驗與數值模擬，但是目前在許多實際工程中存在非中心入射流的情況，例如在空間站中用于水循環的氣相催化脫氨系統（vapor phase catalytic ammonia removal)中的刮膜式旋轉圓盤（wiped film rotating disk)[15-16]，入射流中心與圓盤中心位于不同的位置。Niederhaus 和Hall 等[17-19]雖然對刮膜式旋轉圓盤的刮刷區域進行了實驗研究，但是缺少對入射流沖擊旋轉圓盤形成的進口區的討論。入射流進口的偏移使得水躍的形狀和水躍的半徑發生了變化，液膜的厚度分布極不均勻，進而影響旋轉圓盤的傳熱效率和運轉穩定性。因此，本文將對特定條件下的非中心入射流旋轉圓盤進口區域的水力學現象進行實驗與模擬，研究進口流量和圓盤轉速對水躍的影響。

1 實驗裝置及現象

1.1 實驗裝置

實驗流程如圖1 所示，實驗裝置由進料部分、旋轉圓盤部分和圖像處理部分組成。進料罐中的液體經過離心泵和流量計后，以一定的流量從進口噴嘴垂直射向旋轉的水平放置的圓盤表面，在圓盤表面鋪展成液膜，液體以一定的速度離開圓盤表面后，進入液體回收器中，之后流入回收罐中循環使用。高速攝像機（Photron FASTCAM SA4）位于旋轉圓盤的上方，具體位置和拍照角度可以根據鏡頭（Nikon AF 50mm）需要進行調節。實驗中照相頻率為2000Hz，照片分辨率為1024×1024。實驗中的液體為自來水，圓盤直徑D為300mm，中心旋轉軸直徑Dc為50mm，圓盤表面材質為有機玻璃，與水的接觸角為70°，進口直徑d為3mm，進口位置與圓盤中心的距離e為50mm，進口位置與圓盤表面之間的垂直距離為10mm，水的流量Q的范圍是10～30L/h，圓盤的旋轉速度N的范圍是150～300r/min。為了觀察水在轉盤表面的流動狀態，實驗時在水中加入亞甲基藍固體粉末使自來水呈現深藍色，亞甲基藍水溶液濃度為50mg/L，密度為998kg/m3，黏度為1.004mPa·s，表面張力系數為0.072N/m。

圖1 實驗流程示意圖

1.2 實驗現象

實驗中得到的液膜鋪展照片如圖2所示，圖中進口流量為15L/h，圓盤轉速為150r/min，旋轉方向為逆時針方向。當圓盤的旋轉速度保持穩定后，深藍色的水由進口噴嘴射向圓盤表面，首先在進口部分聚集，隨著時間的增加，水在離心力和黏性力的共同作用下沿著圓盤的旋轉方向開始鋪展成液膜。實驗中的進口流量在10～30L/h 的范圍內，在此流量范圍下液體并不能完全潤濕圓盤表面，會在液膜的最外側形成水躍，水躍外側的液膜破裂，以液線流[20]的形式流出圓盤表面。

圖2 圓盤表面流動形態

中心入射和非中心入射造成的水躍現象的差異如圖3 所示。圖中圓盤旋轉方向均為逆時針方向，進口流量和旋轉速度均保持不變，d為進口直徑，h為過渡區液膜厚度，H為水躍高度。本文定義R1為進口旋轉方向前方的水躍半徑，R為旋轉方向后方的水躍半徑。中心流入射時，圓盤表面的液膜分布基本呈中心對稱，旋轉方向前方的水躍半徑和旋轉方向后方的水躍半徑相等。當入射流不在圓盤中心時，水躍會因為離心力和黏性力的作用發生變化，水躍位置發生了遷移，以進口中心與圓盤中心連線的垂直切面的水躍現象為例，旋轉方向前方水躍半徑明顯小于旋轉方向后方水躍半徑，而且水躍半徑受進口流量和圓盤旋轉速度影響。

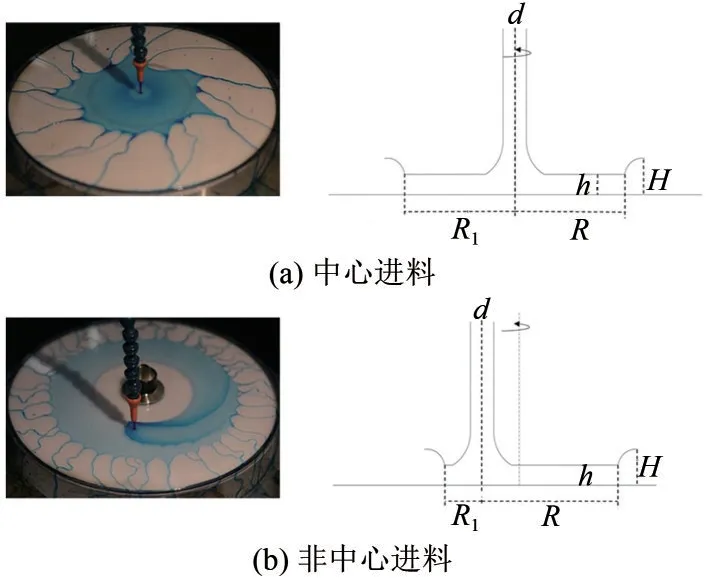
圖3 水躍實驗照片和示意圖

2 數值模擬

2.1 物理模型

計算區域的物理模型如圖4所示。研究所關注的區域僅為旋轉圓盤的進口區域，而且圓盤上水躍之外的液膜對水躍的影響較小[21]，同時由圖2可以看出水躍和鋪展的液膜集中分布在圓盤表面靠近中心的進口區域，因此只針對進口部分進行了模型構建與網格劃分，選取直徑為200mm 的圓盤中包含進口區的1/4扇形區域作為計算域，計算域的高度為5mm，在可以獲得進口部分水躍現象的同時減少了網格的數量，節約計算資源，縮短計算時間。

圖4 物理模型示意圖

2.2 計算模型

本文利用VOF（volume of fluid）多相流模型進行模擬。VOF 模型可以通過求解一組動量方程并跟蹤整個計算域中的兩種流體的體積分數來模擬空氣和水的兩相流。在每一個計算單元中，水和空氣的體積分數α之和等于1，計算式為式(1)。

如果αq=1，則網格中充滿了水；如果αq=0，則網格中充滿了空氣，如果0＜αq＜1，則表示該網格為氣液分界面。VOF 方程中的連續性方程和運動方程為式(2)、式(3)。

式中，ρ為流體的密度，通過體積加權平均得到，如式(4)。

μeff為流體的有效黏度，包括分子黏度μ和湍流黏度μt，計算式為式(5)。

其中分子黏度μ通過體積加權平均得到[式(6)]。

u為速度矢量；t為時間；FV為表面張力，由連續表面CSF模型[22]定義，定義為式(7)、式(8)。

式中，σ為表面張力系數；κ是相界面的曲率；n是表面的法向向量。考慮到液體與旋轉圓盤壁面的接觸角θw，則壁面計算單元表面的法向為式(9)。

式中，nw和tw為壁面計算單位的法向向量和切向向量。

對于入射流撞擊旋轉圓盤的三維模型的計算，Benim等[23]經過比較發現Standardk-ω模型能較好地符合實驗結果，特別是在進口區域部分模擬效果更好。本文研究內容主要針對進口區域的水躍現象，所以選取Standardk-ω模型進行模擬。Standardk-ω湍流模型[24]的方程見式(10)～式(12)。

式中，a為校正系數；k為湍動能；ω為比湍動能耗散率；Γk和Γω分別為湍動能和比湍動能耗散率的有效擴散系數；Gk和Gω分別為由于平均速度梯度產生的湍動能和比湍動能耗散率；Yk和Yω分別為由湍流引起的湍動能和比湍動能的耗散。

入口邊界設置為水相進口，采用速度入口邊界條件，出口為壓力出口邊界條件，操作壓力為標準大氣壓。圓盤表面及旋轉軸軸面均為無滑移固體壁面，給定絕對旋轉速度，旋轉軸為Y軸（圓盤中心軸），圓盤壁面與水的接觸角為70°。入口邊界的湍動能k和比湍動能耗散率ω計算見式(13)、式(14)。

使用ICEM 軟件對物理模型進行網格劃分，對靠近壁面的液體流動的區域采用六面體網格，其余空氣流動的區域采用四面體網格，對壁面處的網格進行加密，壁面第一層邊界層網格厚度為0.01mm，增長率為1.1，層數為10層。網格最大尺寸的范圍控制在0.5～1mm 之間，網格數量的范圍在486 萬～1089萬之間，當圓盤轉速為300r/min、進口流量為20L/h 時，通過綜合比較圓盤表面流體流動形態、旋轉方向后方水躍和計算速度等多方面因素，如表1所示，確定網格數量為759萬。

表1 網格無關性驗證

模擬過程利用商業軟件ANSYS Fluent 16.0 雙精度浮點數求解器進行瞬態計算，壓力速度耦合方式選擇PISO 算法，離散格式的選用如下：梯度采用Least Squares Cell Based 方式離散；壓力采用PRESTO！格式離散；動量采用二階迎風格式；體積分數采用Geo-Reconstruct 插值，湍流動能和耗散率方程采用一階迎風格式。時間步長設置為1×10-5s，計算殘差設定為1×10-4。當出口流量穩定后停止計算。

3 計算結果與討論

3.1 模型驗證

將實驗得到的照片進行圖像銳化處理，再利用ImageJ軟件，以圓盤直徑為標尺，選取與計算域相同的區域，提取圓盤表面的液膜圖像，去除液膜之外的部分，測量液膜的鋪展面積。為了減小實驗誤差，每個操作條件下均隨機選取圓盤系統運轉穩定后（流體入射圓盤表面后穩定1min 以上）的10 張不同的照片進行處理，將最后得到的數據取平均值作為對應操作條件下的鋪展面積。提取計算結果中的氣液交界面[25]作為圓盤液膜表面，如圖5 所示，從圖中可以看到計算結果包含了完整的進口區域的水躍和鋪展液膜，并利用與處理實驗照片同樣的方法統計液膜鋪展面積的計算值。圖6為不同進口流量下鋪展面積實驗值與模擬值的對比圖，從圖中可見計算得到的液膜鋪展面積與實驗值較為接近，表明只針對進口部分進行建模與數值模擬可以獲得較為準確的液膜鋪展情況。由圖6可以看出相同轉速下，隨著進口流量的增大，圓盤表面的鋪展面積逐漸增大，是因為進口流量的增大使得慣性力的作用增大，促進了液膜的鋪展。但是當進口流量相同時，圓盤轉速增加，液膜鋪展面積減小。這是由于進口位于偏離圓盤中心的位置，靠近圓盤中心的液體和靠近圓盤邊緣的液體同時受到離心力的作用，原本有利于液膜鋪展的離心力對進口區液體的作用減小，更多的液體隨著圓盤的旋轉方向運動，從而鋪展面積減小。實驗值和模擬值的平均相對誤差為9%，說明建立的計算模型可以較為準確地再現旋轉圓盤進口區域的流體流動現象。

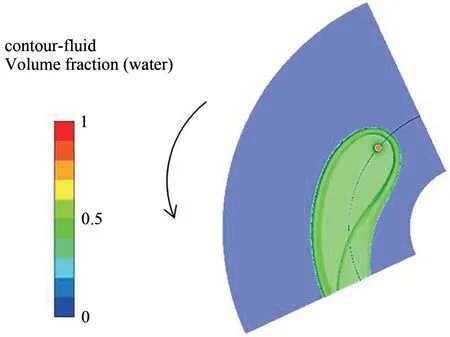
圖5 液膜分布圖

圖6 液膜鋪展面積實驗值和模擬值對比

3.2 進口流量對水躍的影響

圖7表示以圓盤中心為圓心，進口中心到圓心的距離為半徑的環面上的液膜分布圖，圖中橫坐標為圓弧線上各點與進口中心之間的相對距離，坐標為負表示位于進口的圓盤旋轉方向前方，坐標為正表示位于進口的圓盤旋轉方向后方。縱坐標表示液膜表面與圓盤表面之間的距離。不同曲線代表不同的進口流量，圓盤轉速均為300r/min。由圖7可知，在進口的旋轉方向前方，當進口流量較低時，由于慣性作用較小，沒有水躍現象；當進口流量大于20L/h 時，慣性作用增大，發生明顯的水躍現象，水躍高度變化不大，但明顯高于旋轉方向后方的水躍高度。這是因為在旋轉方向前方，液體受到的離心力和慣性力的作用方向相反，離心力會抑制液膜在旋轉方向前方的鋪展，在液膜邊緣形成水躍時，離心力和表面張力的作用方向相同，而在旋轉方向后方離心力有利于液膜的鋪展，形成水躍時離心力和慣性力的作用方向相同，所以在旋轉方向前方，水躍高度明顯高于旋轉方向后方的水躍。在進口的旋轉方向后方，當流量大于15L/h時有明顯的水躍現象，隨著進口流量的增大，水躍半徑由0逐漸增大到48.77mm，水躍高度由1.17mm 減小至0.45mm后達到穩定，穩定區液膜厚度最小為0.09mm，水躍半徑和液膜厚度隨流量的變化如圖8 和圖9 所示。是因為隨著進口流量的增大，慣性力的作用增強，表面張力的作用相對減弱，對液體流動的阻礙作用減弱，液體更容易鋪展。

圖7 液膜分布圖

圖8 水躍半徑隨流量變化

圖9 液膜高度隨流量變化

結合圖10 的速度分布曲線可得，當液體由進口入射到旋轉圓盤表面后，在慣性力的作用下，液體在圓盤表面由入射中心向四周擴散，由于圓盤表面的黏性力作用，液膜速度略有下降，之后由于離心力的作用液膜的速度逐漸增大，最終不同進口流量的液膜速度達到相同的最大值。在液膜鋪展的邊緣，由于表面張力的作用，液膜堆積形成水躍，液體的動能轉化為位能，速度變小。根據液膜的速度變化可以將旋轉圓盤進口區的液膜流動劃分為以下4 個區域：慣性力占主導作用的轉換區、過渡區、離心力占主導作用的穩定區和水躍區。當沒有水躍現象時，旋轉圓盤進口區的液膜流動只有轉化區和過渡區，液膜較厚，鋪展面積較小。當旋轉圓盤表面有明顯的水躍現象時，流量越大，過渡區過渡越平緩，穩定區長度越長，旋轉方向后方水躍半徑越大，液膜更加鋪展。

圖10 液膜速度分布曲線

3.3 圓盤旋轉對水躍的影響

圖11 表示進口中心環面上的液膜分布圖，不同的曲線表示圓盤旋轉速度不同，進口流量均為30L/h。由圖可知，在進口的旋轉方向前方，圓盤旋轉速度越大，離心力相對于慣性力的作用越大，水躍半徑越小，水躍高度越高，當圓盤轉速達到600r/min時，水躍的液膜發生破裂飛濺。在旋轉方向后方，圓盤表面液膜的水躍半徑隨著圓盤轉速的增加先增加后減小，如圖12 所示，在轉速為300r/min 時水躍半徑最大，為48.77mm。這是因為當進口流量為30L/h時，此時的流量不足以潤濕整個圓盤表面，如圖2所示，當液體流動時，存在靠近圓盤中心的液膜邊緣和靠外的液膜邊緣，兩邊均受到離心力的作用，外側受到的離心力有利于液膜向圓盤邊緣鋪展，內側受到的離心力不利于液膜向圓盤中心鋪展。當圓盤轉速較小時，內側離心力的作用相對于慣性力的作用較小，外側離心力的作用占主導作用，所以圓盤轉速增加，水躍半徑增加，液膜更加鋪展；當圓盤轉速較大時，內側受到的離心力作用增強，水躍半徑隨著圓盤轉速的增加而減小。圖13 表示進口旋轉方向后方水躍高度和穩定區液膜厚度隨圓盤轉速變化的趨勢。隨著圓盤轉速的增加，水躍高度由1.20mm 逐漸減小至0.32mm，穩定區液膜厚度由0.17mm逐漸減小至0.07mm。圓盤轉速越大，圓盤對流體的離心作用越大，旋轉圓盤上的液膜向出口運動的趨勢越強，液膜越薄，水躍高度越低。

圖11 液膜分布圖

圖12 水躍半徑隨轉速變化圖

圖13 液膜高度隨轉速變化圖

3.4 水躍半徑預測

由以上分析可知，非中心入射流旋轉圓盤進口區流體流動和水躍現象主要受進口流量和圓盤旋轉速度的影響[13]，即主要影響水躍半徑的因素為進口雷諾數ReJ和圓盤旋轉雷諾數ReD。ReJ和ReD的計算式如式(15)、式(16)所示。

式中，U為進口液體的平均流速；N為圓盤旋轉速度；D為圓盤直徑。分析進口旋轉方向后方的水躍半徑與進口流量和圓盤轉速的關系，擬合得到水躍半徑與ReJ、ReD的經驗關聯式見式(17)。

對比水躍半徑模擬值和預測值，如圖14所示，結果表明大部分模擬值和預測值的誤差在15%以內，說明經驗關聯式可以較好地預測水躍半徑。

圖14 水躍半徑模擬值和預測值對比

4 結論

本文通過實驗對非中心入射流旋轉圓盤進口部分的流體流動進行了觀察，并測量了進口部分液膜的潤濕面積，建立了旋轉圓盤進口部分流體流動過程的CFD模型，得到以下結論。

（1）當圓盤轉速一定時，隨著進口流量的增大，非中心入射流旋轉圓盤進口區的鋪展面積逐漸增大。實驗值與模擬值的平均相對誤差為9%，建立的數值模型可以較為準確地模擬實驗現象。

（2）非中心入射流旋轉圓盤的進口偏離圓盤中心，導致進口旋轉方向前方的水躍和旋轉方向后方的水躍現象明顯不同。當進口流量大于15L/h時會出現明顯的水躍現象，進口旋轉方向前方的水躍高度最高可達2.5mm，旋轉方向后方的水躍高度穩定在0.45mm。旋轉方向后方穩定區液膜厚度最小可達0.07mm。

（3）在進口旋轉方向前方，進口流量越大，圓盤旋轉速度越小，水躍半徑越大。在進口的旋轉方向后方，流量越大，水躍半徑越大，而旋轉速度越大，水躍半徑先增大后減小，當圓盤轉速為300r/min時水躍半徑最大。對進口旋轉方向后方的水躍半徑與進口流量和圓盤旋轉速度的關系進行了擬合并得到關聯式，關聯式的預測結果與模擬結果的誤差在15%以內。

符號說明

D,Dc—— 圓盤直徑和中心旋轉軸直徑，mm

d—— 進口直徑，mm

e—— 圓盤表面進口位置中心與圓盤中心的距離，mm

H—— 水躍高度，mm

h—— 過渡區液膜厚度，mm

k—— 湍動能，m2/s2

N—— 圓盤轉速，r/min

n—— 法向向量

Q—— 進料流量，L/h

R1,R—— 進口旋轉方向前方和后方的水躍半徑，mm

Re—— 雷諾數

t—— 時間，s

t—— 切向向量

U—— 進口液體的平均流速，m/s

u—— 速度矢量，m/s

u—— 黏度，Pa·s

v—— 運動黏度，m2/s

α—— 體積分數

κ—— 曲率，1/m

θw—— 接觸角，(°)

ρ—— 密度，kg/m3

σ—— 表面張力，N/m

ω—— 比湍動能耗散率，1/s

下角標

D—— 圓盤

J—— 進口

w—— 壁面