柔性管纜限彎器等效彎曲剛度研究

丁樂(lè)聲，陳金龍，張 聰，盧青針，岳前進(jìn)

（大連理工大學(xué)a.海洋科學(xué)與技術(shù)學(xué)院；b.盤(pán)錦產(chǎn)業(yè)技術(shù)研究院，遼寧盤(pán)錦 124200）

0 引 言

在海洋油氣、海上風(fēng)電[1]等資源、能源的開(kāi)發(fā)中，海底電纜、管道等柔性結(jié)構(gòu)有著大量應(yīng)用。細(xì)長(zhǎng)結(jié)構(gòu)的海洋柔性管纜在復(fù)雜的海洋環(huán)境載荷下極易發(fā)生過(guò)度彎曲、疲勞等破壞模式[2]。因此，美國(guó)石油協(xié)會(huì)（API）在其頒布的標(biāo)準(zhǔn)中指出，應(yīng)在與剛性結(jié)構(gòu)連接的柔性管道、海纜上安裝彎曲限制器[3]，并且不同環(huán)境荷載下不同柔性管纜的限彎器需要分別設(shè)計(jì)。

限彎器主體是多節(jié)圓筒相互嵌套的周期性結(jié)構(gòu)，當(dāng)柔性管道或纜與限彎器形成的組合體彎曲至限彎器的鎖合半徑時(shí)[4]，其各節(jié)互相接觸、鎖合而提供更大的彎曲剛度，阻止柔性管道或纜過(guò)度彎曲。因此，限彎器的彎曲剛度是其核心設(shè)計(jì)指標(biāo)。

限彎器形狀復(fù)雜，完全獨(dú)立的幾何參數(shù)有7個(gè)[5]，而限彎器彎曲剛度設(shè)計(jì)工作涉及公頭端部高度、有效節(jié)長(zhǎng)、母頭尾部厚度、材料彈性模量等參數(shù)，是一個(gè)多參數(shù)設(shè)計(jì)問(wèn)題。在缺乏有效力學(xué)模型時(shí)，限彎器設(shè)計(jì)多依賴經(jīng)驗(yàn)，導(dǎo)致效率低下。在已有工作中，O'Regan 等[6]首先基于ABAQUS 軟件給出了限彎器彎曲分析模型，主要研究螺栓緊固結(jié)構(gòu)對(duì)限彎器彎曲強(qiáng)度的影響；Noh 等[7]基于ABAQUS 進(jìn)行了限彎器與纜的多體接觸分析，并對(duì)限彎器結(jié)構(gòu)進(jìn)行了拓?fù)鋬?yōu)化；張聰[8]提出了組合彎曲剛度是限彎器關(guān)鍵力學(xué)指標(biāo)，并給出了基于有限元分析的限彎器等效彎曲剛度計(jì)算方法。

為提高限彎器設(shè)計(jì)效率，需進(jìn)一步對(duì)其等效彎曲剛度開(kāi)展理論研究與參數(shù)影響分析。本文基于歐拉-伯努利梁理論建立了限彎器總體純彎梁模型，并采用板彎曲理論與Hertz 接觸理論建立總體模型中的鎖合結(jié)構(gòu)模型，通過(guò)簡(jiǎn)化得出計(jì)算限彎器等效彎曲剛度的半經(jīng)驗(yàn)求解形式，還分析了關(guān)鍵參數(shù)對(duì)限彎器等效彎曲剛度的影響趨勢(shì)；然后建立有限元模型驗(yàn)證半經(jīng)驗(yàn)求解形式與關(guān)鍵參數(shù)影響趨勢(shì)，并在研究參數(shù)影響規(guī)律時(shí)引入高效的正交試驗(yàn)方法。

1 限彎器等效彎曲剛度理論研究

限彎器結(jié)構(gòu)包含如圖1 所示的諸多參數(shù)。為減少設(shè)計(jì)變量，考慮到限彎器肩部長(zhǎng)度通常與外徑保持一定比例關(guān)系，本文引入有效節(jié)長(zhǎng)l，它表示單節(jié)限彎器對(duì)柔性管纜的有效覆蓋長(zhǎng)度，分為頸長(zhǎng)l1與肩部長(zhǎng)度l2，即l=l1+l2；當(dāng)調(diào)節(jié)有效節(jié)長(zhǎng)時(shí)只改變頸長(zhǎng)以保證與肩部長(zhǎng)度相關(guān)的外徑不變。同時(shí)認(rèn)為限彎器彎曲形變符合小變形、平截面假定，忽略接觸區(qū)域的摩擦效應(yīng)，且將材料視為線彈性。

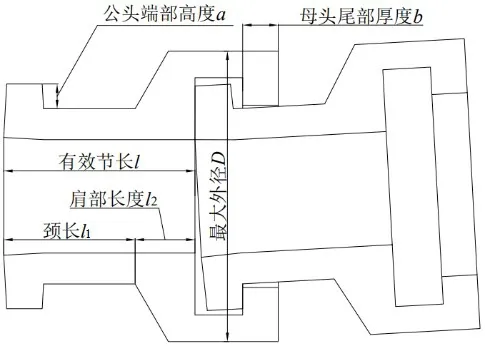
圖1 限彎器裝配Fig.1 Assembly of bend restrictor

根據(jù)上述簡(jiǎn)化及假設(shè)，可以基于歐拉-伯努利梁理論、板彎曲理論與Hertz 接觸理論，分別從總體和局部考慮建立限彎器的理論模型，并研究公頭端部高度a、有效節(jié)長(zhǎng)l、母頭尾部厚度b三類形狀設(shè)計(jì)參數(shù)，以及材料彈性模量E對(duì)限彎器等效彎曲剛度的影響。

1.1 限彎器總體純彎梁模型

限彎器總體由變徑圓筒形的子梁結(jié)構(gòu)與鎖合結(jié)構(gòu)交替組成，可簡(jiǎn)化成如圖2所示的純彎梁模型。

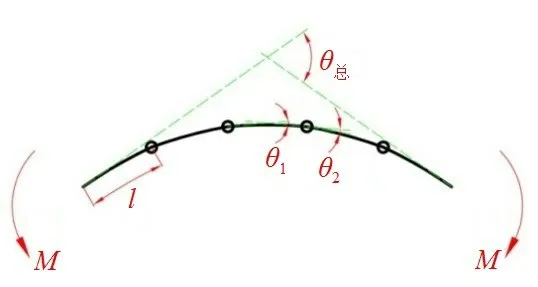
圖2 限彎器總體純彎梁模型Fig.2 Global pure bending beam model of bend restrictor

基于歐拉-伯努利梁理論，給出子梁結(jié)構(gòu)純彎公式如下[9]：

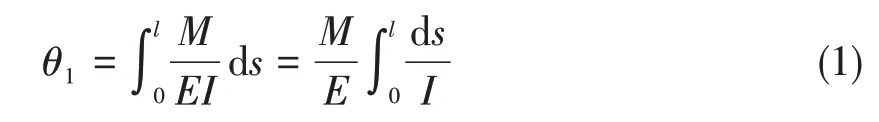
式中，θ1為子梁彎曲轉(zhuǎn)角，M為彎矩，l為有效節(jié)長(zhǎng)，E為材料彈性模量，I為截面慣性矩。

式中，D為外徑，d為內(nèi)徑，則式（1）中的積分可根據(jù)形狀參數(shù)進(jìn)行計(jì)算，簡(jiǎn)化為

此處引入鎖合結(jié)構(gòu)彎曲剛度G，則鎖合結(jié)構(gòu)彎曲轉(zhuǎn)角

由式（3）和式（4）可以計(jì)算得組合結(jié)構(gòu)的總轉(zhuǎn)角

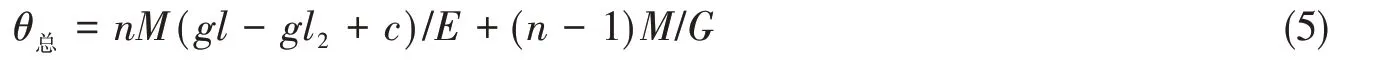
式中，n為總體中子梁結(jié)構(gòu)數(shù)量，再依據(jù)梁理論給出限彎器的等效彎曲剛度為

聯(lián)立式（5）和式（6）可以得到限彎器總體純彎梁模型為

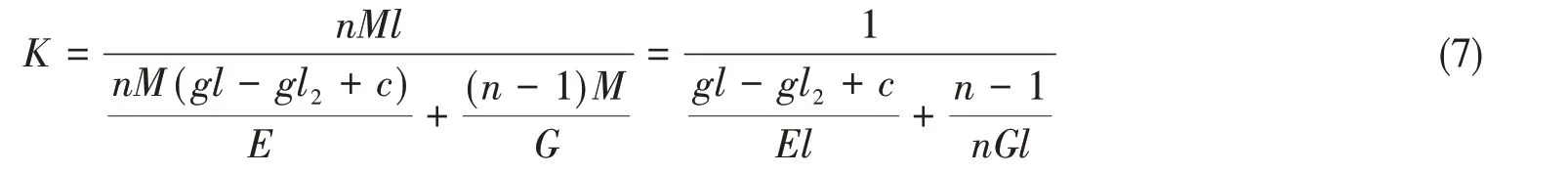
式中，鎖合結(jié)構(gòu)彎曲剛度G將在下一節(jié)進(jìn)行研究。

1.2 局部鎖合結(jié)構(gòu)彎曲模型

限彎器局部鎖合結(jié)構(gòu)如圖3所示。當(dāng)限彎器鎖合時(shí)，公頭與母頭發(fā)生接觸、傳遞彎矩。從圖中可以看出，公頭端部與母頭的上半部接觸剛度相對(duì)較大，其接觸變形可忽略不計(jì)，故可以假設(shè)此處為鎖合結(jié)構(gòu)旋轉(zhuǎn)中心，則其轉(zhuǎn)動(dòng)半徑r為公頭端部中徑；基于此，該過(guò)程可簡(jiǎn)化為兩圓環(huán)局部接觸、彎曲的力學(xué)模型。

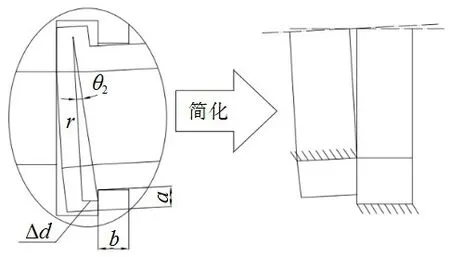
圖3 局部鎖合結(jié)構(gòu)Fig.3 Local locking structure restrictor

由幾何約束得到鎖合結(jié)構(gòu)彎曲轉(zhuǎn)角，即

式中：Δd為形變產(chǎn)生的接觸處軸向位移，r為轉(zhuǎn)動(dòng)半徑。當(dāng)Δd/r較小時(shí)可省略高階量，將式（8）簡(jiǎn)化為

形變產(chǎn)生的接觸處軸向位移由接觸形變?chǔ)1、公頭端部撓度w1和母頭尾部撓度w2三部分組成，即

同時(shí)，將公頭所受接觸力簡(jiǎn)化為沿公頭端部高度a這一徑向方程均勻分布的線性荷載q，則

值得注意的是，該荷載在接觸面的圓周方向是非連續(xù)的。

Hertz接觸理論被廣泛地用于曲面接觸問(wèn)題計(jì)算[10]。忽略掉切向摩擦力并假設(shè)接觸物體足夠大可形成彈性半空間，則引入材料泊松比μ后，限彎器公頭端部與母頭尾部的接觸變形可描述為

環(huán)形板彎曲理論可解決公頭端部與母頭尾部的彎曲問(wèn)題，其本構(gòu)方程如式（13）所示[11]：

式中：D為板彎曲剛度[11]，w為撓度，δ為厚度，ρ為徑向尺寸，q'為荷載。

局部鎖和結(jié)構(gòu)彎曲模型由式（4）和式（9）-（13）組成，但式（13）中含有邊界條件不連續(xù)的二維重調(diào)和方程；下一節(jié)將探索其簡(jiǎn)化形式，以獲得形式簡(jiǎn)單便于工程應(yīng)用的解。

1.3 等效彎曲剛度的半經(jīng)驗(yàn)求解形式

當(dāng)限彎器公頭端部及母頭尾部的徑向尺寸為定值時(shí)，根據(jù)疊加原理可引入系數(shù)k將式（13）線性化；再將母頭尾部厚度b與公頭端部厚度e代入，得到簡(jiǎn)化的彎曲模型如式（14）-（15）所示：式中：D1、D2分別為公頭端部與母頭尾部的彎曲剛度，k1、k2是為了將式（13）線性化而引入的系數(shù)，它們分別與公頭端部和母頭尾部的徑向尺寸ρ呈非線性負(fù)相關(guān)。將式（4）、式（9）-（12）、式（14）-（15）聯(lián)立得

3.2 測(cè)驗(yàn)。測(cè)驗(yàn)包括階段性測(cè)驗(yàn)、單元測(cè)驗(yàn)或隨堂考試等，主要偏重考察學(xué)生對(duì)歷史事實(shí)類知識(shí)性內(nèi)容的了解和掌握。考核方式的選擇是按照本課程設(shè)定的了解、領(lǐng)會(huì)、掌握及分析應(yīng)用等不同教學(xué)要求，歸置為不同的客觀題型，次數(shù)不限，考試時(shí)間可長(zhǎng)可短，授課中或授課告一階段后，教師都可以進(jìn)行。測(cè)驗(yàn)較之課堂提問(wèn)覆蓋面全且標(biāo)準(zhǔn)客觀統(tǒng)一，測(cè)驗(yàn)后及時(shí)反饋，便利于同學(xué)們及時(shí)發(fā)現(xiàn)自己的問(wèn)題，強(qiáng)化同學(xué)們對(duì)基本歷史事實(shí)的掌握。測(cè)驗(yàn)占到平時(shí)成績(jī)30%。

進(jìn)一步將式（16）代入式（7）得到了一種針對(duì)模型（14）的解析解，

式中，g為式（3）中頸部截面極慣性矩的倒數(shù)，c為式（3）中的定積分常數(shù)，l2為肩部長(zhǎng)度，H為鎖合結(jié)構(gòu)剛度系數(shù)，

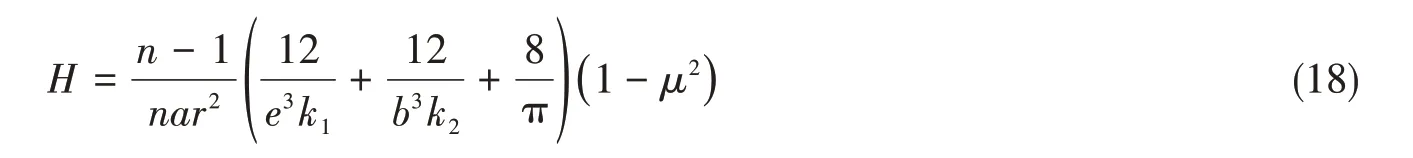
需要注意，當(dāng)公頭端部及母頭尾部的徑向尺寸不變時(shí)，系數(shù)k1、k2即為定值。并且系數(shù)k1、k2無(wú)法通過(guò)理論方法直接獲得，可結(jié)合有限元方法或試驗(yàn)分析利用式（14）-（15）計(jì)算。在獲取k1、k2之后，即可通過(guò)公式（17）-（18）求解限彎器等效彎曲剛度。

1.4 參數(shù)影響規(guī)律

通過(guò)以上理論研究，可以獲得如下參數(shù)影響規(guī)律：

（1）公頭端部高度a是一個(gè)公頭端部的徑向尺寸，式（13）中表示為ρ；由式（13）-（14）可知其與系數(shù)k1呈非線性負(fù)相關(guān)；即公頭端部高度a增大時(shí)，式（18）中k1減小，從而使H增大，但同時(shí)由式（13）可知，a本身增大亦使H減小。綜上，由式（17）可知公頭端部高度a與等效彎曲剛度呈非線性關(guān)系。

（2）由式（17）計(jì)算等效彎曲剛度K關(guān)于有效節(jié)長(zhǎng)的導(dǎo)數(shù)為

式中，g為頸部截面極慣性矩的倒數(shù)，c為式（3）中的常數(shù)，H可由式（18）求得，l2為肩部長(zhǎng)度。當(dāng)滿足判據(jù)式（20），即限彎器為短肩結(jié)構(gòu)時(shí)，K'恒為正數(shù)，有效節(jié)長(zhǎng)l與等效彎曲剛度正相關(guān)。

（3）由式（17）-（18）可知，母頭尾部厚度b和材料彈性模量E與等效彎曲剛度正相關(guān)。

2 等效彎曲剛度計(jì)算與參數(shù)影響分析

本章基于實(shí)際的限彎器參數(shù)，建立有限元分析模型驗(yàn)證理論研究獲得的半經(jīng)驗(yàn)求解形式和各參數(shù)對(duì)等效彎曲剛度的影響。在研究上述四類參數(shù)影響時(shí)引入了正交試驗(yàn)設(shè)計(jì)方法，以提高效率。

2.1 彎曲剛度計(jì)算示例

選擇公頭端部與母頭尾部徑向尺寸、材料泊松比相同的兩組實(shí)際限彎器參數(shù)作為算例A 與B，尺寸及材料參數(shù)詳見(jiàn)表1，算例參數(shù)化截面如圖4所示。

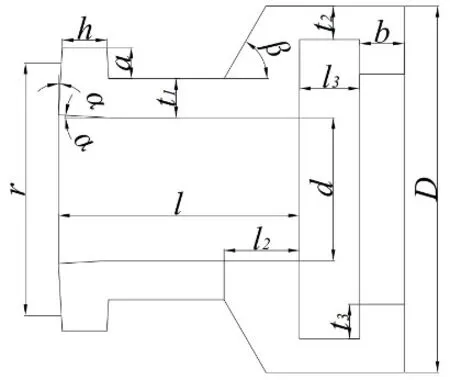
圖4 限彎器算例尺寸Fig.4 Example dimensions of bend restrictor

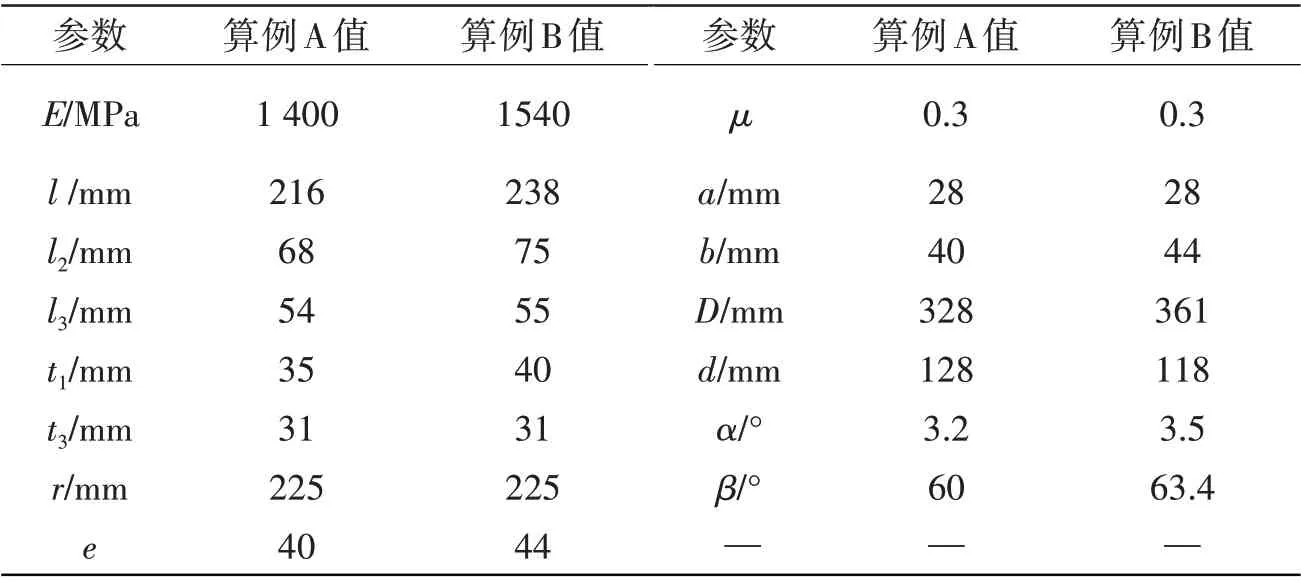
表1 限彎器結(jié)構(gòu)參數(shù)表Tab.1 Parameters of bend restrictor structure

等效彎曲剛度可通過(guò)有限元法計(jì)算。基于ABAQUS，利用結(jié)構(gòu)對(duì)稱性對(duì)上述算例A與B分別建立參數(shù)化的三維模型，并選擇懸臂梁純彎曲加載，對(duì)前端施加3 kN·m 的彎矩，對(duì)尾端施加完全固定約束，如圖5所示。

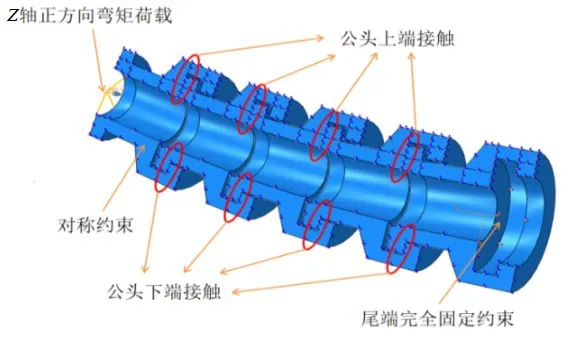
圖5 限彎器相互作用及邊界條件設(shè)置Fig.5 Interaction of bend restrictor and boundary condition setting

模型共有8個(gè)接觸對(duì)，法向行為選擇硬接觸算法，切向行為則選擇罰函數(shù)算法。最后從有限元結(jié)果中提取端部轉(zhuǎn)角，并由式（6）計(jì)算等效彎曲剛度，結(jié)果如表2所示。半經(jīng)驗(yàn)求解需計(jì)算系數(shù)k1、k2；算例A 與B 的公頭端部與母頭尾部徑向尺寸相同，因此系數(shù)k1、k2也相同。故先基于上文所述有限元方法分析算例A 定彎矩下公頭端部撓度w1及母頭尾部撓度w2，并根據(jù)式（11）、（14）-（15）求得系數(shù)k1、k2。最終將表1中各參數(shù)代入式（17）-（18）分析算例A與B等效彎曲剛度，結(jié)果在表2中給出。

表2 等效彎曲剛度計(jì)算結(jié)果Tab.2 Calculation results of equivalent bending stiffness

由表2 可知，半經(jīng)驗(yàn)求解結(jié)果與有限元法計(jì)算結(jié)果的誤差小于5%，可有效計(jì)算限彎器等效彎曲剛度。且當(dāng)系數(shù)k1、k2已知時(shí)，僅需將限彎器參數(shù)代入公式即可快速計(jì)算其等效彎曲剛度。

2.2 正交試驗(yàn)設(shè)計(jì)

通常4 因素4 水平的全因素試驗(yàn)，需要進(jìn)行44次處理，而正交試驗(yàn)設(shè)計(jì)分析只需要處理42次。故選用正交試驗(yàn)設(shè)計(jì)[12]方法，分析滿足判據(jù)式（20）的短肩限彎器；各結(jié)構(gòu)參數(shù)水平如表3所示，將參數(shù)代入L16（45）正交表[12]，并以有限元分析得到的等效彎曲剛度K作為評(píng)價(jià)指標(biāo)進(jìn)行計(jì)算。

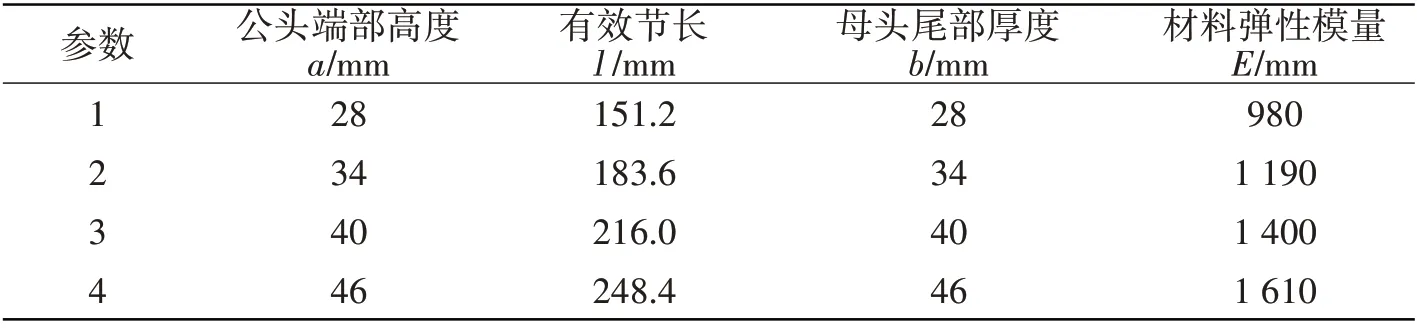
表3 限彎器模型主要參數(shù)水平Tab.3 Main parameters of the limited bender model

2.3 參數(shù)影響程度分析結(jié)果

在正交試驗(yàn)的基礎(chǔ)上引入指標(biāo)總和Ji、指標(biāo)均值ji，以及極差R以判斷各個(gè)因素對(duì)限彎器等效剛度的影響程度。

本試驗(yàn)分析結(jié)果于表4給出，四類參數(shù)對(duì)等效彎曲剛度的影響如圖6所示。

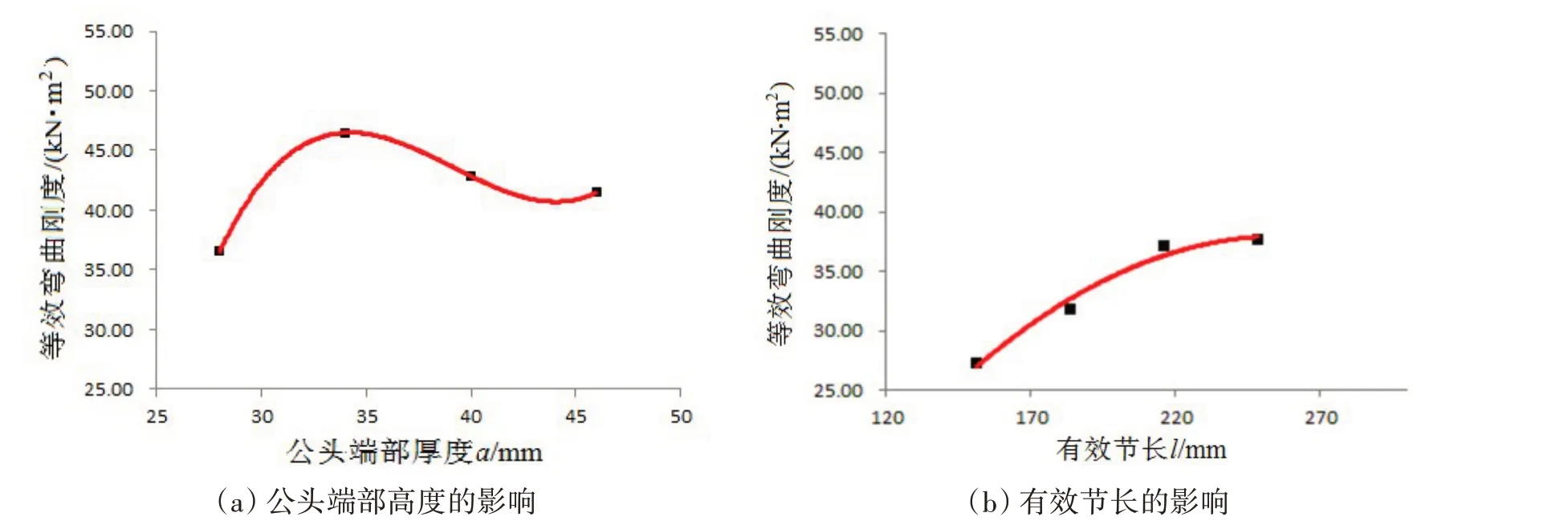
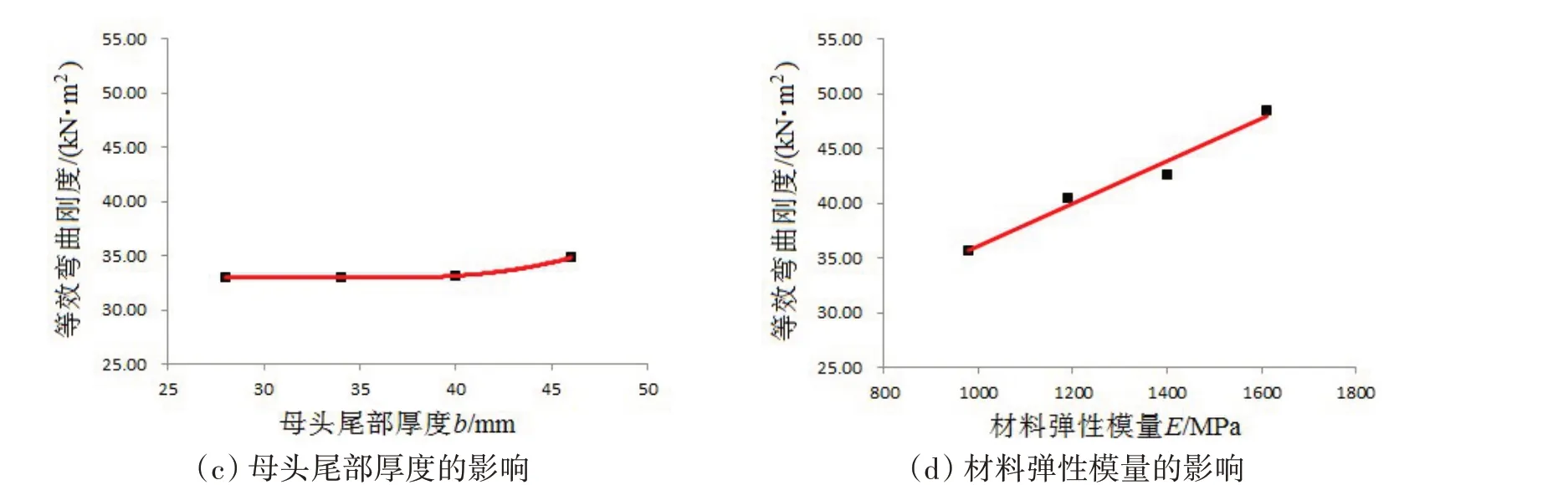
圖6 四類參數(shù)對(duì)等效彎曲剛度的影響Fig.6 Influence of four type parameters on equivalent bending stiffness

表4 正交試驗(yàn)法分析結(jié)果Tab.4 Analysis results of orthogonal test

對(duì)比表4 中各因素極差值發(fā)現(xiàn)，材料彈性模量影響最大，其次是有效節(jié)長(zhǎng)和公頭端部高度，母頭尾部厚度的影響最小。

如圖6 所示，隨著公頭端部高度增大，等效彎曲剛度呈先增大后減小趨勢(shì)；當(dāng)限彎器為滿足判據(jù)式（20）的短肩結(jié)構(gòu)時(shí)有效節(jié)長(zhǎng)與等效彎曲剛度正相關(guān)；母頭尾部厚度及材料彈性模量與等效彎曲剛度正相關(guān)。有限元分析得到的四參數(shù)影響趨勢(shì)與理論研究吻合。

3 結(jié) 論

本文基于歐拉-伯努利梁理論建立了限彎器等效彎曲剛度的總體純彎梁模型，采用板彎曲理論與Hertz接觸理論建立總體模型中的局部鎖合結(jié)構(gòu)彎曲模型；并得出簡(jiǎn)化的限彎器等效彎曲剛度計(jì)算半經(jīng)驗(yàn)求解形式，同時(shí)基于模型研究了公頭端部高度、有效節(jié)長(zhǎng)、母頭尾部厚度、材料彈性模量四類參數(shù)對(duì)等效彎曲剛度的影響規(guī)律。然后通過(guò)有限元分析以及正交試驗(yàn)設(shè)計(jì)方法進(jìn)一步驗(yàn)證與分析，獲得如下結(jié)論：

（1）通過(guò)簡(jiǎn)化限彎器等效彎曲剛度的總體純彎梁模型，可以得到半經(jīng)驗(yàn)求解形式；并且半經(jīng)驗(yàn)求解形式經(jīng)有限元法驗(yàn)證是有效的。

（2）隨著公頭端部高度增大，等效彎曲剛度先增大后減小，當(dāng)限彎器為短肩結(jié)構(gòu)時(shí)有效節(jié)長(zhǎng)與等效彎曲剛度正相關(guān)，母頭尾部厚度及材料彈性模量與等效彎曲剛度正相關(guān)。

（3）通過(guò)分析四類參數(shù)對(duì)限彎器等效彎曲剛度的影響程度，發(fā)現(xiàn)其影響主次因素順序?yàn)椴牧蠌椥阅Ａ俊⒂行Ч?jié)長(zhǎng)、公頭端部高度、母頭尾部厚度。

本文通過(guò)引入有效節(jié)長(zhǎng)概念，將限彎器結(jié)構(gòu)設(shè)計(jì)簡(jiǎn)化為四個(gè)變量進(jìn)行研究。事實(shí)上，限彎器各部分內(nèi)徑等結(jié)構(gòu)參數(shù)，也對(duì)等效彎曲剛度有影響。同時(shí)，限彎器結(jié)構(gòu)參數(shù)在設(shè)計(jì)時(shí)會(huì)受到所保護(hù)管纜的結(jié)構(gòu)性能的影響，可以在未來(lái)進(jìn)一步研究。