基于土拱效應的單樁水平極限承載力分析

王衛中，李永輝

(1.河南省交通規劃設計研究院股份有限公司，鄭州 450000；2.公路地質病害防治技術河南省工程實驗室，鄭州 450000；3.鄭州大學 土木工程學院，鄭州 450001)

樁作為工程中常用的受力構件，其承受的荷載較為復雜。在一些工程中，水平荷載成為控制樁基設計的重要因素。對于水平受荷樁，根據樁土相對剛度的大小，其破壞模式分別為剛性轉動破壞和柔性彎曲破壞，對應的單樁可分別稱之為剛性短樁和柔性長樁。由于剛性短樁的承載特性較柔性長樁簡單，為了較為簡便地獲得柔性長樁的極限承載力，MEYERHOF[1]以及POULOS et al[2]建議將柔性長樁等代為剛性短樁進行計算分析。對于剛性短樁，在僅承受水平荷載時，樁體自身變形可以忽略，樁體作為剛體繞某一點轉動，在達到極限荷載時，樁體被動側土體達到極限。眾多學者[3-6]采用被動側土體為楔形體破壞模式來計算樁側土體極限抗力，但是忽略了楔形破壞體中的土拱效應，與實際情況不符。當剛性短樁在水平荷載的作用下繞一點轉動時，樁與樁側土間及各相鄰土層間產生相對位移趨勢，進而導致土層的主應力方向發生偏轉，從而在破壞的楔形體內形成顯著的土拱效應。

根據前人研究，結構物后土拱可以假設為圓弧拱[7]、拋物線拱[8]和懸鏈線拱[9]。本文在計算柔性長樁水平極限承載力時，將柔性長樁等代為剛性短樁，然后考慮被動側土體的楔形體破壞模式及土拱效應，推導了樁后土壓力系數與水平微分單元層間摩擦系數的理論公式，得到了剛性單樁水平極限承載力的改進計算方法，并與國內外實驗數據進行了對比和驗證。

1 考慮土拱效應的剛性樁樁側土體極限抗力分析

1.1 樁后主應力拱分析

樁頂在水平荷載p作用下并朝向土體方向轉動達到極限時，樁后土體受壓并達到被動極限平衡狀態。假設破壞模式與REESE[10]關于樁周上部土體破壞楔形體模式相似，如圖1所示，圖中α=φ/2.同時，考慮到土體與樁側的摩擦角δ，根據庫侖土壓力理論，其滑裂面傾角β的計算公式為

(1)

式中：β為破壞面與水平面的夾角，φ為土體的內摩擦角，α為破裂面擴散角，δ為土體和樁的外摩擦角。

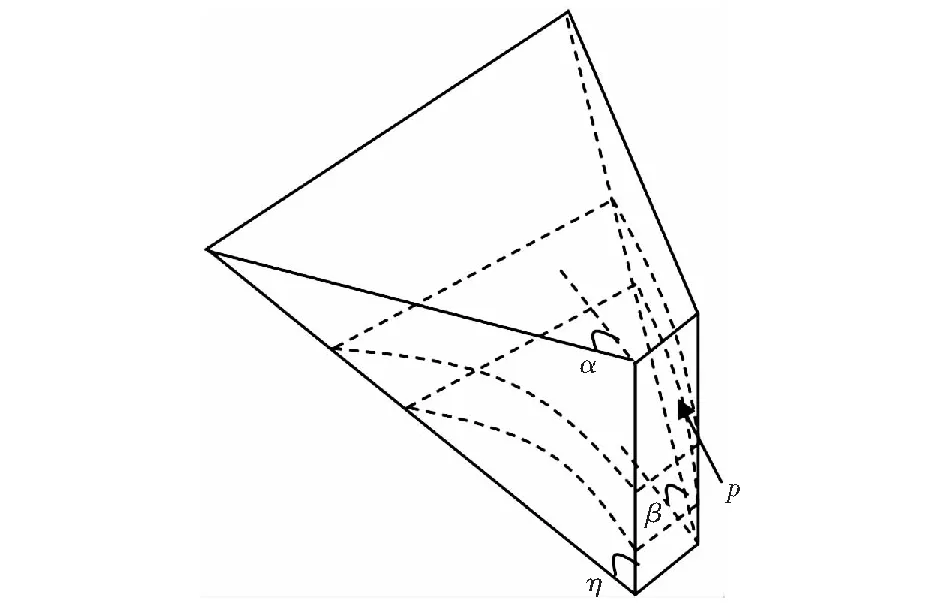
圖1 樁前楔形體破壞模式及樁前土拱Fig.1 Failure mode of wedge and soil arch of pile

樁體發生水平位移時，樁土間的摩擦角逐漸發揮，被動側土體主應力發生偏轉，在土體中形成向上凸的大主應力軌跡線，即為大主應力拱。假設楔形破壞體內的主應力軌跡線為圓曲線，如圖2所示。

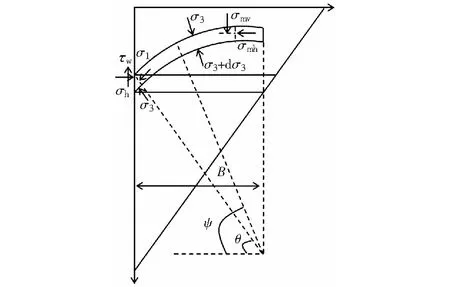
圖2 樁被動側土體大應力拱分析Fig.2 Large stress arch of passive zone of pile

拱跡線上任一點大主應力σ1的方向相切于拱跡線，小主應力σ3的方向垂直于拱跡線。圖2中B為圓弧拱的圓心與樁迎土側間的水平距離；σmh為圓弧拱微元體水平應力分量；σmv為圓弧拱微元體豎直應力分量；ψ為圓弧拱半徑與水平方向的夾角。

1.2 任意深度樁土界面位置主應力旋轉角θ

在任意深度樁土界面位置，圖3所示為摩爾應力圓的樁邊處剪應力。

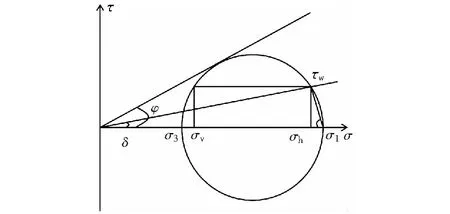
圖3 樁邊處單元土體摩爾應力圓Fig.3 Mohr stress circle of unit soil at pile edge

(2)

水平應力：

σh=σ1-τwcotθ.

(3)

由式(2)和式(3)得：

σh=σ1sin2θ+σ3cos2θ.

(4)

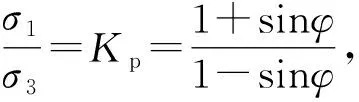
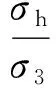
(5)

由圖3可知σv-σ3=σ1-σh，故

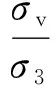
(6)

同理可得出拱跡線上任意一點：

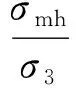
(7)

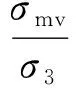
(8)

水平剪應力

τmv=(σ1-σ3)sinψcosψ.

(9)

對于樁邊處主應力旋轉角θ值：

由圖3得：

τw=(σ1-σh)tanθ=σhtanδ.

(10)

由式(4)及式(5)得

(11)

由式(10)及式(11)可得：

(12)

解上式可得到兩個θ值，較大值對應被動土壓力的情況，由此得出樁邊處主應力旋轉角：

(13)

1.3 圓弧形拱跡線分析

由式(8)-式(10)可知，對于圓弧拱任意位置處單元體豎向正應力σmv、水平向正應力σmh以及相應的斜截面的剪應力τmv的大小皆與M點處應力旋轉角ψ有關。下面推導ψ與樁邊處土體單元應力旋轉角θ的關系。

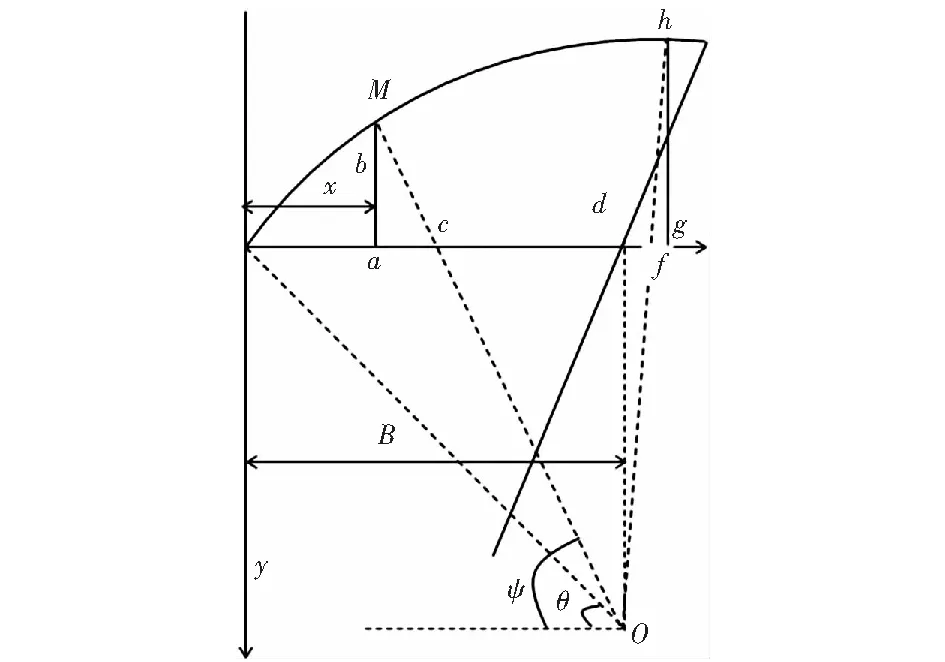
圖4 圓弧拱形分析Fig.4 Arc arch analysis

由圖4，三角形abc和三角形doc相似，故

將ob=B/cosθ，oc=Btanθ/sinψ，cd=Btanθcotψ,ad=B-x代入上式，可得

故

(14)

x>B時：三角形odf和三角形fgh相似，同時將oh=B/cosθ，of=Btanθ/cos(ψ-π/2)，df=Btanθtan(ψ-π/2)，dg=x-B代入上式，可得sin(ψ-π/2)=(x-B)cosθ/B

故

(15)

因此x無論為何值，式(14)及式(15)始終成立。

將式(15)分別代入式(8)、式(9)和式(10)得：

(16)

(17)

(18)

1.4 側土壓力系數Kwp與層間摩擦系數tanφ′

計算樁側土壓力時，側土壓力系數Kwp定義為樁邊處水平應力σh與水平單元平均豎向應力σav之比，而不是σh與樁邊處單元土體σv之比。由此得：

(19)

任意深度水平單元σmv/σ1的平均值為

(20)

取任意深度z0樁主動側破壞楔形體的某一水平面，如圖5所示。設樁徑為b，則式(20)中A=(B+Btanα)，dA=(2xtanα+b)dx.

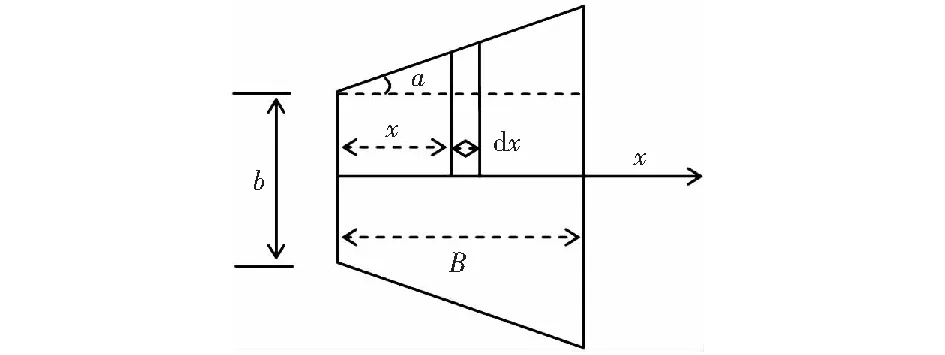
圖5 破壞楔形體平面示意圖Fig.5 Plane diagram of failure wedge

則由式(19)及式(20)得

(21)

對于繞底轉動的樁體，采用水平單元法計算樁側土體抗力時，水平層間存在剪應力。根據文獻[8]中關于水平微分單元層間摩擦系數tanφ′的定義，認為微分單元平均水平剪應力τav與平均豎向正應力σav的比值，即：

(22)

將式(18)代入上式并整理后得：

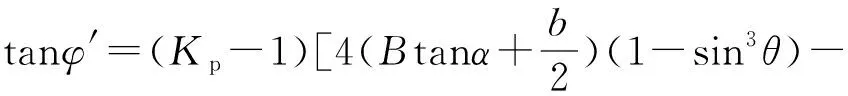
(23)

1.5 樁后土體抗力計算基本方程及其解答

在楔形體內任一深度z處，取一厚度為dz的水平微分單元，得到樁后土壓力分析模型如圖6所示。作用于微分單元上的力包括：土體自重形成的豎向力dW=γdV；單元上、下表面的平均垂直壓應力σav和(σav+dσav)及平均剪應力τav和τav+dτav；樁體水平反力σh；樁體與樁側土體摩擦力τh；作用于單元兩側的切向應力τh以及法向應力fn，作用于滑裂面的法向應力r及剪應力τ.各應力的作用方向如圖6所示。

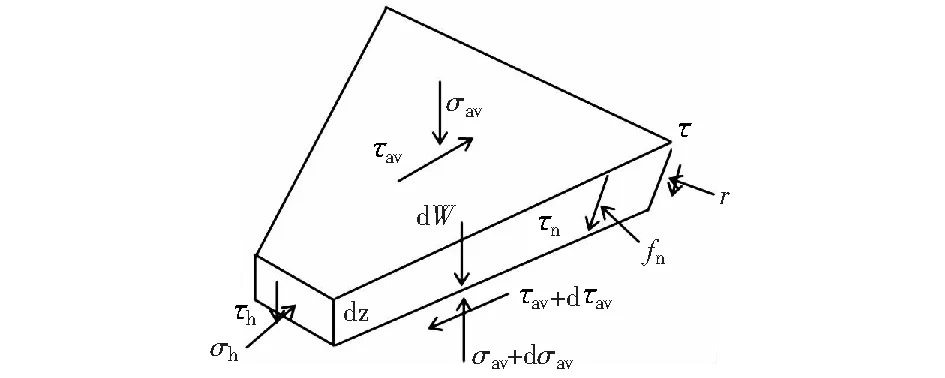
圖6 樁后土體抗力計算簡圖Fig.6 Calculation diagram of soil resistance of passive zone

根據豎向力平衡：

σavA2-A1dσav+τhbdz+dW+2τncosηA3+
τsinβA4-rcosβA4=0 .

(24)

式中：A1為單元下表面積，A2為單元上下表面積差，A3為單元側表面積，A4為單元滑裂面面積。

令τh=σhtanδ，σh=Kwpσav，τn=k0γytanφ，τ=rtanφ，代入式(24)得：

σavA2-A1dσav+Kwpσavtanδbdz+γdV+
2k0γztanφcosηA3+rtanφsinβA4-rcosβA4=0 .

(25)

式中：dV為水平微分單元體積，η如圖1中所示。

根據單元體水平力平衡得：

τavA2-A1dτav+σhbdz-2τnsinηcosαA3+
2fnsinαA3-τcosβA4-rsinβA4=0 .

(26)

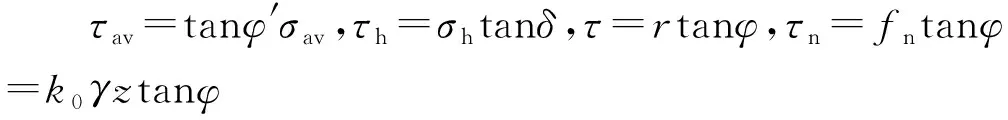
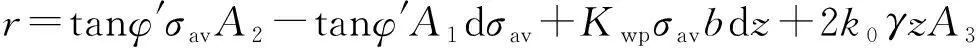
(27)

將式(27)代入式(25)并整理得出：

lσav-mdσav+dW+n=0 .

(28)

式中：

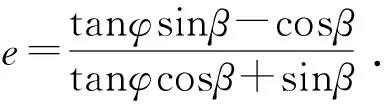
1.6 計算過程

上述計算樁側土體抗力的公式(28)可以采用差分方法進行解答。解答過程如下：

1) 根據已知條件求取β值和θ值；

2) 將樁主動側土體破壞楔形體沿深度分為n段：每段長度為dz=H/n，第一段邊界條件為：σav[0]=q，q為地面堆載；

3) 根據式(22)以及式(24)求取第1段中點處的Kwp[1]和tanφ′[1]，式中B[1]=[H-(i-1)×dz-dz/2]·ctgβ；

4) 根據式(28)求取dσav[1]，則σav[1]=dσav[1]+σav[0]；

5) 重復步驟(3)-(4)，依次求取第2，3…n段，最終得出σav[i]，i∈[0，n]；

6) 由σh[i]=Kwp[i]·σav[i]可以得出某一深度處樁側土體極限抗力。

2 水平極限承載力分析

對于砂土中的水平受荷樁長樁等代長度Leu與L的關系采用式(29)確定[11]。

Leu/L=1.8(Krs)0.12≤1 .

(29)

式中：Leu為長樁等代長度；L為柔性長樁樁長。

(30)

式中：Krs為樁土相對剛度；Eh為樁端位置處土體水平反力模量；d為樁徑。定義Krs>10-1為剛性短樁，Krs<10-1為柔性單樁。

圖7為水平荷載作用下剛性短樁樁側土體極限抗力沿樁體埋深的分布模式[3，12]。在已知樁體尺寸以及砂土土體性質的情況下，樁側土體極限承載力pu可根據上節分析獲得，由砂面處樁體截面的受力平衡，聯立求解式(31)和式(32)，即可得出a及水平極限承載力Fu.

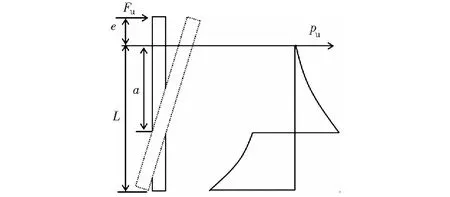
圖7 水平荷載下樁側土體極限抗力分布模式Fig.7 Distribution pattern of ultimate resistance of soil around pile under horizontal load

(31)

(32)

采用上節考慮土拱效應的極限土壓力對相關文獻的剛性短樁極限承載力進行了計算，同時對文獻[17]的室內模型試驗進行了分析。室內模型試驗采用的模型樁經式(30)計算得出的Krs為1.45×10-4，小于10-2，因此為柔性樁，采用式(29)將柔性模型樁等代為剛性短樁，得出等代長度為903.8 mm，所得計算結果與相關文獻計算結果一并見表1。由表1可知，計算結果與實測結果誤差在-25.0%～22.6%之間，但主要在-4%～10%之間波動，計算結果與實測結果誤差相對較小。另外平均誤差為2.9%，可見采用本文方法所得計算結果能夠滿足工程要求。另外由室內模型試驗結果可以看出，將柔性長樁等代為剛性短樁可以較為簡單并合理得出長樁的水平極限承載力。因此，對于柔性長樁，可以將其等代為剛性短樁，然后采用本文計算方法確定水平極限承載力。

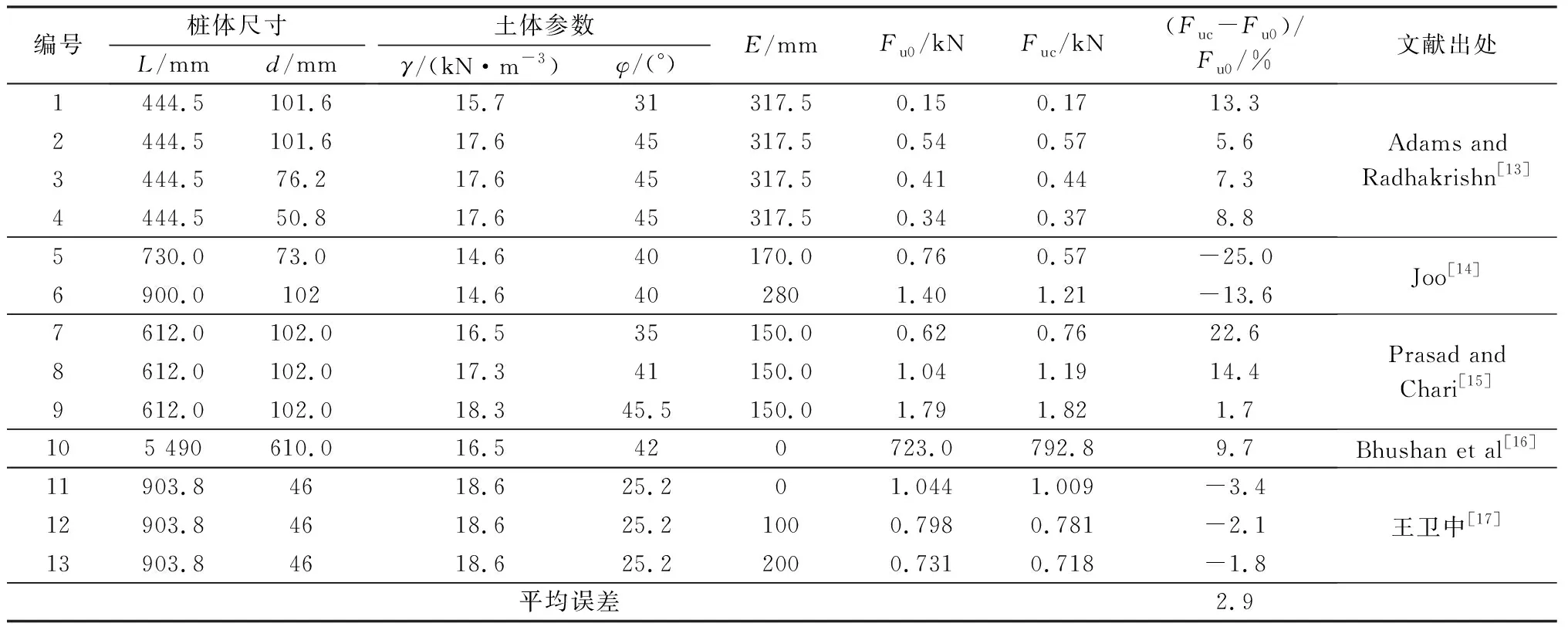
表1 剛性短樁水平極限承載力計算結果與實測結果對比Table 1 Companson of calculation results of horizontal ultimate bearing capacity with measurd results

3 結論

1) 將柔性長樁等代為剛性短樁，基于樁后土體破壞楔形體的土拱效應，推導了樁后土壓力系數，得到了柔性單樁水平極限承載力的改進計算方法。

2) 和已有研究成果以及相關模型試驗數據進行了對比分析。計算結果表明，本文考慮土拱效應的計算方法能夠較為理想地反映試驗結果，對柔性單樁的水平極限承載力確定具有一定的指導意義。

3) 本文方法僅能得出柔性單樁的水平極限承載力。對于想要獲得樁頂位移及樁體內力，仍需要采用其他方法進行計算。