露天礦外排土場粒徑及土層厚度對表土滲透規律影響

馬 力，羅 強，武 璟，畢銀麗，彭蘇萍，薛 飛

(1.西安科技大學 a.能源學院，b.地質與環境學院，西安 710054；2.中國礦業大學(北京) 煤炭資源與安全開采國家重點實驗室，北京 100083)

露天開采挖損大量的土地，礦體以上巖層結構完全被剝離掉。同時，用于排棄剝離物料的外排土場壓占土地，使土地生態功能退化。針對露天礦山排土場開展復墾與生態修復，是降低礦山開采影響及提高生態功能的重要途徑。排土場是在松散物料堆棄基礎上形成并重新鋪設的表土，用于植物種植，其特點為物料松散、蓄水性差。表土中水分影響土壤理化性質和土壤肥力，對植物生長發育產生重要影響，并制約著露天礦生態修復效果及經濟成本。為有效恢復露天礦區生態功能，實施土地復墾與生態修復勢在必行。因此，對外排土場表土進行滲透性研究，可為土地復墾與生態重建提供科學依據。

針對土的滲透性規律，國內外眾多學者做了相關研究。王紅等[1]采用土柱實驗及多元回歸分析對重塑黃土的非飽和滲透系數進行研究，得到滲透系數與體積含水率、滲透系數與基質吸力的函數關系。張鎮飛等[2]采用常水頭滲透實驗對壓實黃土中的水分垂直入滲規律和非飽和滲透系數函數進行了研究，并采用VAN GENUCHTEN[3]和FREDLUND[4]等滲透系數模型分別對50 cm干密度1.45 g/cm3和1.55 g/cm3的非飽和滲透系數進行預測，發現VAN GENUCHTEN滲透系數模型預測結果更接近實測值。胡明鑒等[5]開展了不同細粒徑含量的鈣質砂滲透性試驗研究，確定當最小粒徑≤0.075 mm時，鈣質砂呈中透水性，當最小粒徑介于0.075～0.500 mm時，鈣質砂呈高透水性。

此外，一些學者通過試驗分析了不同因素對滲透系數的影響。梁建偉等[6]為研究極細顆粒黏土的滲透特性，對極細顆粒人工土和廣州南沙天然軟土進行滲透實驗。研究確定隨著孔隙液離子濃度的增大，試樣的滲透系數隨之增加；隨著水力梯度的降低，對于不同離子濃度的孔隙液情況，試樣的滲透系數增大或者減小。楊兵等[7]分析了級配對砂土滲透性的影響規律，研究得出滲透系數隨砂土的平均粒徑增大而增大。蘇立君等[8]通過單一粒徑級砂土常水頭滲透試驗，研究了同一孔隙率下不同粒徑級砂土滲透系數隨均值粒徑的變化規律，結果顯示，滲透系數隨孔隙率、均值粒徑二次方的增加而線性增加。藺曉燕等[9]對不同深度的黃土試樣進行不同壓力下土的固結-滲透實驗，得出室內常規變水頭滲透試驗所得黃土滲透系數較固結-滲透試驗所測得數據大25～40倍。ONUR[10]在達西定律的基礎上建立了一系列較為全面的砂土滲透理論，確定砂土的粒徑分布指數與滲透性密切相關。曹志翔等[11]基于泊肅葉定律，把層流滲流土體等效為細管簇，建立了滲透物理模型，并結合Darcy定律推導出了以等效粒徑和孔隙率作為基本參數的滲透系數理論計算公式。

目前關于土壤的滲透性研究眾多，但對于露天煤礦外排土場表土的滲透性研究開展較少，尤其是針對露天礦外排土場表土粒徑和土層厚度對滲透特性相關程度的影響研究。本文以露天礦外排土場表土開展不同粒徑與土層厚度的滲透性研究，揭示粒徑與厚度對滲透特性的影響，為露天煤礦土地復墾和生態修復提供指導。

1 表土滲透規律物理模擬方法

1.1 定水頭表土滲透規律土柱試驗方案

土的滲透性是由骨架粒徑之間孔隙構成水的通道所致，實質上是水在土體孔隙中流動的現象[12-13]，是表征土體被水透過的能力。土柱實驗采用壁厚0.5 cm、外徑15 cm、內徑14 cm、高度為50 cm的圓筒，圓筒由亞克力材料制成，每個圓筒孔眼的數目為20個，孔眼的半徑為0.5 cm，試驗原理及裝置如圖1所示。

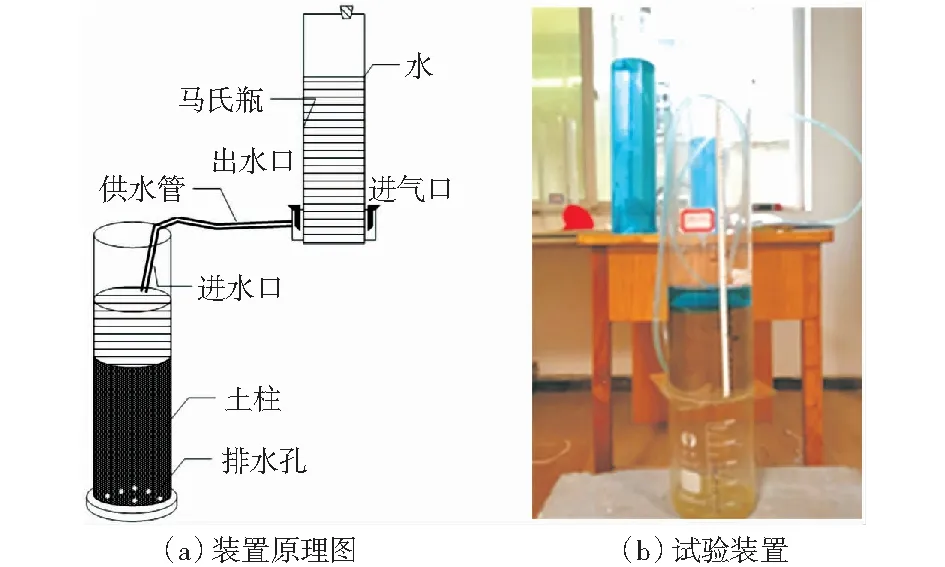
圖1 試驗原理及裝置圖Fig.1 Test principle and device diagram

將土樣晾干并使用標準篩分篩，將所需粒徑0.5 mm、1 mm、2 mm土樣篩分出，各個粒徑的鋪設厚度分別為5 cm、10 cm、15 cm、20 cm；所需物料經幾次制備夠用后各自放入儲物筐備用[14]。在裝樣前先在圓筒底部鋪上一層紗網，防止物料將孔眼堵塞，裝填完成后用同等質量、內徑大小與試驗圓筒內徑相同的砝碼對圓筒中的土樣進行壓實，保證試驗各土柱具有相同的密實度，試樣制備完靜置24 h備用。試驗共12組，為提高實驗結果的準確性，對每組試驗進行三次重復試驗并對其實驗結果取平均值。

1.2 滲透系數及入滲速率測定方法

1.2.1滲透系數K的測定

對表土樣本采用常水頭土柱法測定入滲過程，通過實驗測定試樣厚度、試樣橫截面積、常水頭滲透裝置水位差、滲透時間、燒杯水量等以計算滲透系數K，計算公式如下[15]：

(1)

式中：K為滲透系數，cm/s；L為試樣厚度，cm；A為試樣截面積，cm2；L為滲徑(即試樣厚度)，cm；Q為入滲量，cm3；t為時間，s；h為常水頭，cm.

1.2.2入滲速率的測定

將土樣加入到圓筒中，采用馬氏瓶進行供水。測定時，采用馬氏瓶維持土面3 cm的積水深度，分時間段記錄圓筒加入的水量。入滲0～5 min每隔30 s記錄一次，入滲5～30 min每隔1 min記錄一次，入滲30 min后每隔5 min記錄一次，當至少3次相同時間內圓筒供水量恒定時可視為達到穩定，停止試驗。燒杯中的水量根據燒杯的高度進行換算，對應入滲速率的計算方法為[16]：

(2)

式中：f(t)為入滲速率，cm/min；ΔV為某一段時間內馬氏瓶加入的水量，cm3；S為土樣橫截面積，cm2；Δt為時段，min；θ為試驗過程中的平均水溫，℃.

1.3 粒徑及土層高度對滲透性的影響規律

通過實驗，確定馬氏瓶穩定下降高度，并依據式(1)、式(2)確定滲透系數以及穩定入滲速率，實驗結果如表1所示。

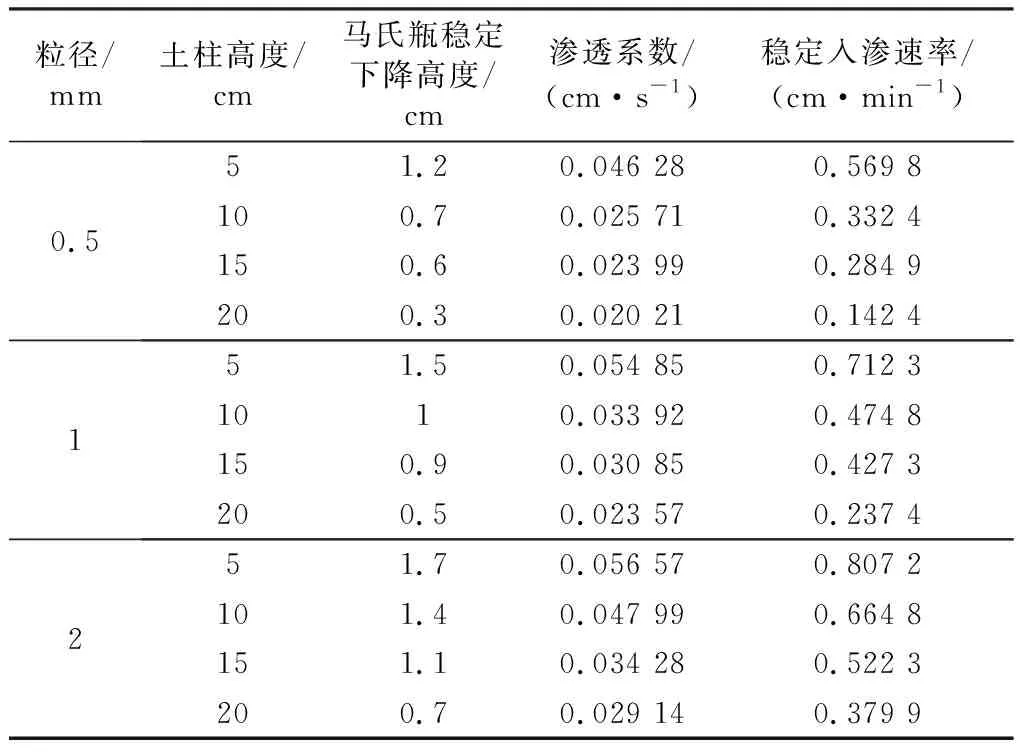
表1 實驗數據處理結果匯總Table 1 Calculated results of experimental data

擬合獲得不同粒徑及土層厚度條件下馬氏瓶下降高度與時間函數關系如表2所示，其中t為時間，min，hm為馬氏瓶液面下降高度，cm.各個擬合函數的優度見表3.

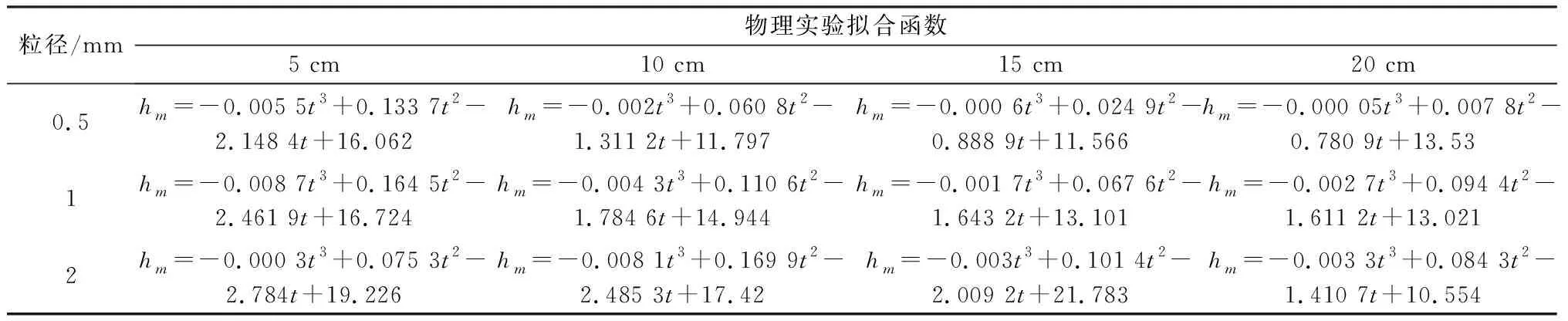
表2 物理實驗擬合函數Table 2 Fitting function of physical experiment

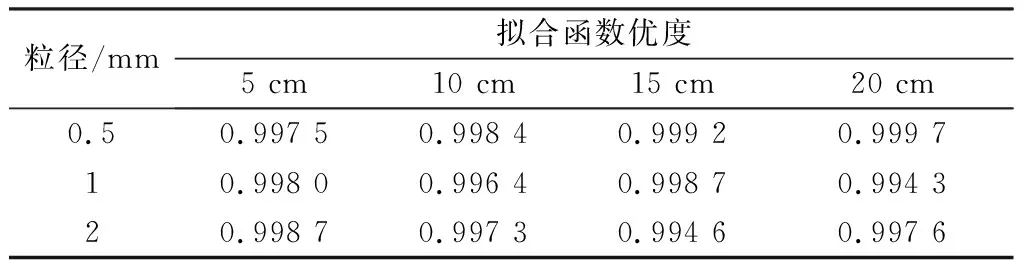
表3 擬合函數優度Table 3 Goodness of fitting function

圖2(a)中馬氏瓶下降高度與時間關系曲線的斜率代表入滲速率，入滲速率大體上呈現由快到慢的趨勢，并且在土柱吸水達到飽和狀態后，滲透速率稍有增加并趨近穩定；2 mm粒徑、鋪設厚度5 cm土柱入滲速率最大，其土樣間隙較大，骨架粒徑之間空隙構成的水通道多，滲透性好；0.5 mm粒徑、鋪設厚度20 cm土柱入滲速率最小，其土樣間空隙較小，骨架粒徑之間空隙構成的水通道較少，并且在入滲過程中伴有少量的泥化現象，滲透性能較差。

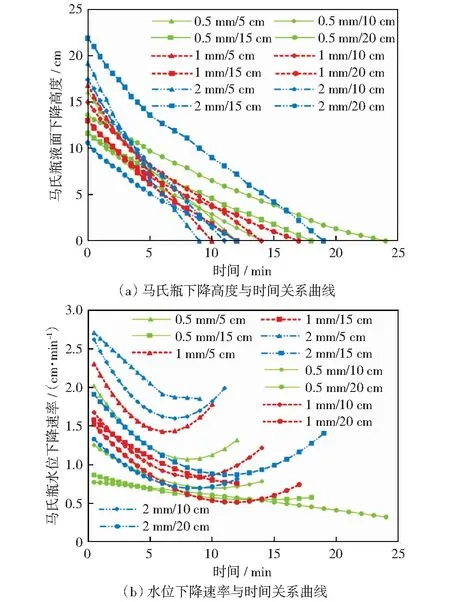
圖2 馬氏瓶下降高度及下降速率與時間關系Fig.2 Relationship between the descending height of the Markov bottle and the descending rate with time

依據試驗結果繪制穩定入滲速率與土層厚度及粒徑關系曲線見圖3。從圖3可以看出，不同粒徑的土層穩定入滲速率均隨土層厚度增大而降低，且相同土層厚度條件下，粒徑越大其穩定入滲速率越大。

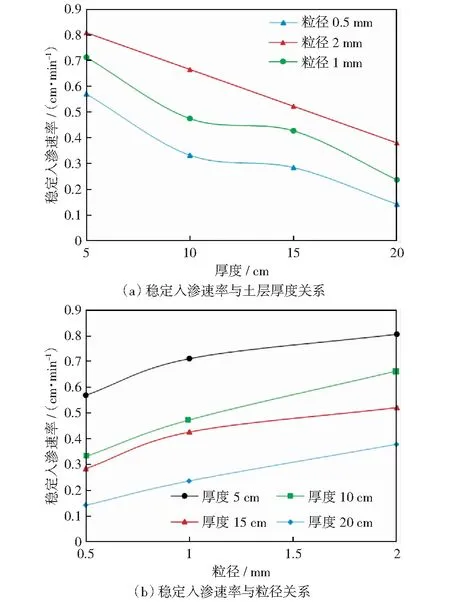
圖3 穩定入滲速率與土層厚度及粒徑關系曲線Fig.3 Relation curve of stable infiltration rate with soil thickness and particle size

依據表3，各個擬合函數的優度均較大，擬合函數的準確性高。

2 粒徑及土層厚度影響的穩態滲流數值模擬

水壓力和水流速變化達到穩定值后，便一直處于這個狀態。當進行穩態分析時，在給定的邊界值和恒定水頭滲流特征下進行[17]；并且在分析過程中沒有初始壓力，持續時間為實驗時間并設置適合的步數，將比例設定為1∶10，對一種粒徑的表土分別構建5 cm、10 cm、15 cm、20 cm四種不同高度。

根據水流連續性等條件，當滲透系數主方向與坐標方向一致時，平面滲流應滿足如下微分方程[18]：

(3)

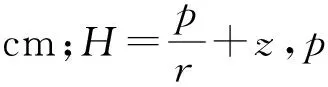
邊界條件通常有以下三類：

1) 邊界上水頭H已知，即H=H0；

2) 邊界上流入或流出的水量已知，此時邊界面上應滿足下列流量平衡式：

(4)

式中：lx、ly為邊界的法向余弦；q為單位邊界表面的流入或流出量，cm3.

對該模型設定第一類滲流邊界條件，模型頂部采用水頭邊界函數，兩側采用總流量為零、底部設置壓力水頭為零的邊界條件，獲得如圖4所示的粒徑為1 mm不同鋪設厚度的土柱模擬云圖。

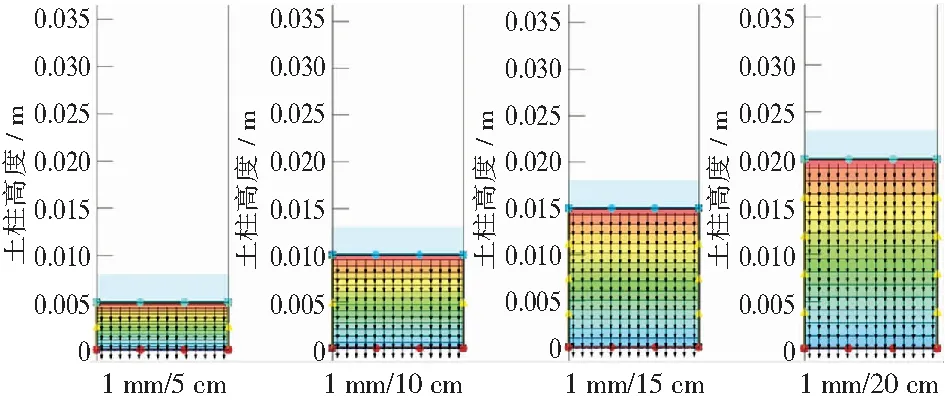
圖4 土柱模擬Fig.4 Soil column simulation

以物理實驗水頭高度、試驗時長、馬氏瓶下降量和燒杯水量作為數值模擬的參數依據，獲得不同模擬方案的下滲速率穩定時的累積水流量、入滲速率變化曲線如圖5所示。

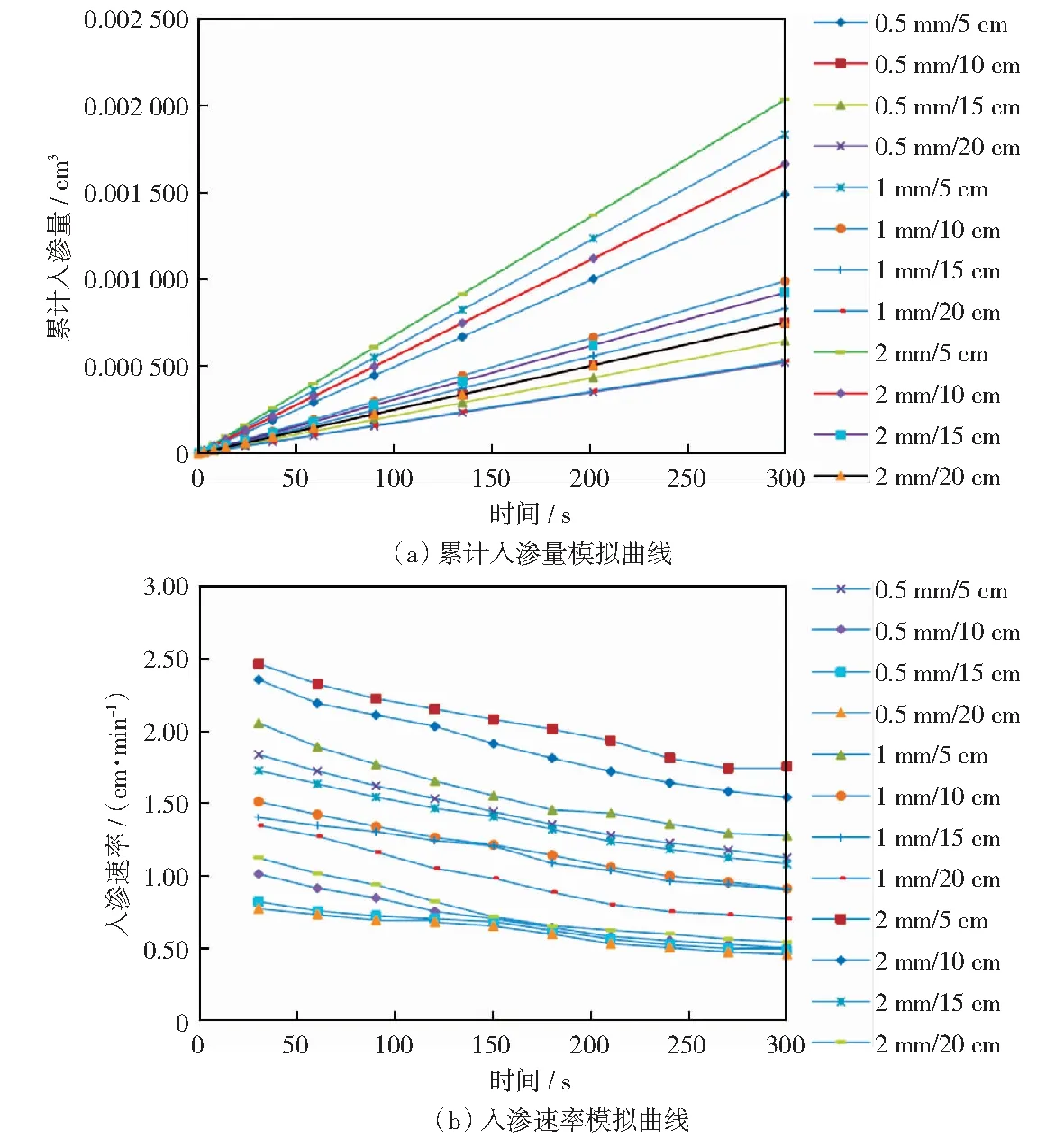
圖5 數值模擬結果分析Fig.5 Analysis of numerical simulation results

根據圖5(a)數值模擬結果，在相同土層粒徑條件下，累計入滲量隨著土層厚度的增加而減小且穩定入滲速率隨著土層厚度的增加而減小；在相同土層厚度條件下，累計入滲量隨著粒徑的增大而增大且穩定入滲速率隨著粒徑的增大而增大。根據圖5(b)數值模擬結果，在相等粒徑條件下，入滲速率隨厚度增大而減小；在相同厚度條件下，入滲速率隨粒徑的增大而增大。

將模擬結果與物理實驗滲透速率、累計入滲量進行對比，結果表明物理實驗與模擬結果基本一致。

3 滲透性影響因素關聯分析

3.1 灰色關聯分析

灰色關聯度分析方法是一種因素比較分析法，其中包含了一個參考序列與多個比較序列，對各因素的時間序列進行比較，從而確定各因素對參考序列影響程度大小。其基本思想是以相關因素的動態數據作為依據，運用數字方法研究因素與因素之間的幾何對應關系[19]。

灰色關聯分析的基本原理是：對統計序列幾何關系進行比較，以此分清系統中各個因素之間的關聯程度，若序列曲線的幾何形狀越接近，則代表了它們之間的關聯程度越大。根據關聯度的大小次序，可以對各因素在系統中的地位做出判斷[20-21]。

具體步驟為：1) 確定分析序列矩陣；2) 對變量序列進行均值無量綱化；3) 求差序列、最大差和最小差；4) 計算關聯系數；5) 計算其余序列與序列的鄧氏關聯度。

3.2 基于灰色關聯度的滲透規律影響因素分析模型

結合表1中確定的12組實驗數據，以滲透系數為參考序列、粒徑和厚度為比較序列，構成滲透系數關聯序列矩陣為：

(5)

對變量序列進行均值無量綱化，其中無量綱化采用的公式為：

(6)

式中：i為關聯序列矩陣中的行數，共3行；k為關聯序列矩陣中的列數，共12列；

采用公式(6)對式(5)進行無量綱化處理，獲得無量綱化矩陣：

(7)

將兩組比較序列和參考序列分別做差值，計算得到差序列，形成絕對值差值矩陣：

Δo1=[0.000 0 0.401 5 0.151 7 0.568 1 0.394 0 0.099 6 0.045 3 0.484 9 0.204 5 0.174 1 0.136 4 0.107 3],

Δo2=[0.000 0 0.098 5 1.151 7 0.181 9 2.394 0 1.400 4 2.454 7 3.484 9 1.545 5 2.575 9 3.636 4 3.642 7].

(8)

對關聯系數進行計算，其計算公式為：

(9)

式中：ζ為關聯系數；i為比較序列數，i=1,2；k為試驗組數，k=1,2,…,12；ρ為分辨系數，ρ∈[0,1]，一般取0.5；Δmin和Δmax分別為差值矩陣中的最大數(最大差)與最小數(最小差)，計算得到最大值、最小值分別為：3.642 7，0.000 0.

由公式(9)得到粒徑和厚度兩類因素各12組數據的關聯系數為：

ζo1=(1.000 0,0.819 4,0.932 1,0.762 2,0.822 1,0.948 1,0.975 7,0.789 8,0.899 1,0.912 8,0.930 3,0.944 4) ,

ζo2=(1.000 0,0.948 7,0.612 6,0.909 2,0.432 1,0.565 3,0.425 9,0.343 2,0.541 0,0.414 2,0.333 7,0.333 3) .

(10)

關聯度的計算公式為：

(11)

依據公式(11)，得到粒徑、土層厚度與滲透系數之間的鄧氏關聯度分別為0.894 7，0.571 6，粒徑與滲透系數之間的相關程度更高。

4 結論

1) 在相等粒徑條件下，滲透速率隨厚度增大而減小；在相同厚度條件下，滲透速率隨粒徑的增大而增大。0.5 mm粒徑較1 mm、2 mm粒徑入滲速率小，應適當在復墾土體中增加小粒徑成分，這對提高表土的持水性具有積極作用。

2) 采用有限元穩態分析法進行滲流數值模擬，在同等粒徑不同厚度條件下，1 mm粒徑、5 cm土層厚度入滲性能較1 mm粒徑、20 cm土層厚度更好，數值模擬充分地驗證了物理實驗的準確性。

3) 依據灰色理論對粒徑、厚度滲透性能的相關性進行計算，得出粒徑、土層厚度與滲透系數K的相對關聯度分別為0.894 7、0.571 6，與土層厚度對比，土樣粒徑對滲透性能的影響程度更大。