基于動態情緒驅動的人員應急疏散模型

李佳洋, 唐加福,2, 郭恩銘

(1. 東北大學 工商管理學院, 遼寧 沈陽 110819; 2. 東北財經大學 管理科學與工程學院, 遼寧 大連 116025; 3. 東北大學 計算機科學與工程學院, 遼寧 沈陽 110169)

人員動態疏散模型是應急疏散研究的重要工具,模擬突發事件的真實情境是評估模型的一個重要指標[1-2].在微觀模型中,元胞自動機(cellular automata,CA)具有模擬復雜系統時空動態演變的能力,并且原理簡單、計算效率高,因此在運動主體動態行為分析等方面得到了廣泛應用. Burstedde等[3]提出“靜態場”和“動態場”的概念,由此構建場域CA模型用以研究個體的疏散特征. Zheng等[4]提出了一種擴展的CA模型以分析三維煙霧擴散對個體疏散行為的影響. Zhang等[5]考慮行人對距離的認知差異并對背景場規則進行修正,構建了基于背景場的粒子群優化算法的出口選擇策略.

情緒等心理狀態在個體行為決策中起著非常重要的作用,從而影響個體運動.近年來,研究人員逐漸關注疏散模型如何表達個體的情緒狀態. Helbing等[6]建立了一個模擬個體在緊急情況下緊張情緒和逃離動態行為的模型. Zheng等[7]提出了一種改進的地板場CA模型,分析了危機的擴散和個體情緒對疏散行為的影響. Cocking等[8]通過實證分析指出,緊急疏散時情緒能在人群中快速傳播,即便是陌生人之間依舊可以傳播.情緒的模型化是一個難題,如何表述情緒的更迭和動態演化,并將情緒狀態的動態性嵌入行人運動模型,是目前疏散模型構建的一個難題.Mao等[9]從研究同伴行為互動的角度,提出了一個基于親密關系的情緒傳染模型來模擬緊急疏散中的同伴決策機制. Fu等[10]將流行病學SIR(susceptible-infectious-removal)模型與CA結合,認為在某種程度上,情緒傳染類似于疾病的傳播,每個個體可能處于三種狀態之一:易感(S)、感染(I)或恢復(R),據此提出了一個新的情緒傳染模型.梳理現有文獻,情緒傳播及更新是一個復雜的過程,當前疏散建模中考慮情緒因素的動態疏散行為方面研究是有限的,情緒的動態更新和行為決策結合的模型仍需要研討.

在突發事件下,情緒會影響人們的判斷和行為決策[11].而傳統傳染病SIS(susceptible-infectious-susceptible)模型考慮到個體很難達到完全免疫,僅存在易感者和感染者這兩種人群,更加符合行人的情緒傳播特性,因此本文在SIS模型基礎上提出一種改進的情緒傳染模型.本文基于SIS傳染模型定義疏散個體狀態,考慮個體速度變化和方向感知域,構建一種符合行人疏散特征的情緒更新機制,并將情緒傳播動力學與行人運動結合,改進轉移概率,建立動態情緒驅動的行人運動模型,最后對模型進行疏散過程仿真,分析微觀情緒傳染演化模型、情緒傳染機理對總疏散時間和安全疏散人數的影響.該模型有助于應急管理者了解緊張情緒在人與人之間傳播特征,便于制定有效的管控策略.

1 經典傳染病模型

不同的情緒強度不僅對個體產生影響,其本身可以通過疏散個體之間的情緒感染而蔓延,而情緒傳染類似于傳染病的傳播[10].傳統的傳染病學模型主要有兩類:SIR模型和SIS模型.

SIR模型是指個體狀態為“易感者”、“感染者”、“免疫者”三種類型.S,I,R分別表示三類群體占總群體的比例.SIR模型在傳染過程中不計算新出生率和死亡率,故S+I+R=1.該模型反映了人群傳染的宏觀過程:當傳染疾病發生時,三類人群總數量恒定,“易感者”一旦與“感染者”接觸,以β概率被傳染;“感染者”以一定的概率γ轉變到“免疫者”;“免疫者”等同于疫苗注射者,對疾病免疫，不再被傳染.

另一種經典SIS模型考慮某些疾病傳染時個體很難達到完全免疫,因此在傳染過程中僅存在“易感者”和“感染者”.該模型的微分系統動力學方程如式(1)所示,狀態轉移如圖1所示.

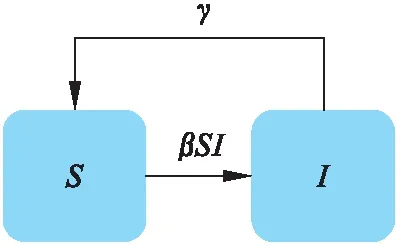
圖1 SIS模型狀態轉移示意圖

(1)

式中:β為日接觸傳染率;γ為日治愈率.

由于SIS模型采用常微分方程表示傳染動力學宏觀模型,是一個宏觀、靜態數學模型,并不適合用于描述疏散個體的微觀情緒感染和自由移動個體狀態;并且SIS模型假定人群總數在傳染過程中不發生變化,而疏散時行人一旦離開出口即為安全,在危險區的人數每時每刻都是變動的.綜上,經典SIS并不完全適用.本文結合CA構建突發事件下考慮情緒感染的行人疏散動態模型.

2 情緒傳染機制

2.1 狀態定義

當室內突發異常事件,如火災、有毒氣體擴散、非法侵害等,行人均帶有緊張情緒.因室內空間有限,個體對危機認知及心理承受能力的差異,具有不同情緒狀態.模型中疏散個體根據其緊張情緒值分為潛在情緒狀態和顯著情緒狀態.

2.2 情緒感染機制

疏散個體情緒值與自身持有情緒及周圍他人情緒相關[9],定義PEj(t)表示t時刻個體j的緊張情緒強度值,取值范圍(0,1],即在疏散全過程中個體不存在緊張情緒消失的時刻.個體j的緊張情緒強度值隨著時間變化的動態方程如式(2)所示.

PEj(t)=PEj(t-1)+(1-ξ)·Δej(t)+τ.

(2)

其中:Δej(t)表示t時刻個體j情緒感知增量;ξ是感知衰減系數,取值范圍[0,1],體現了情緒感知非理性;τ為隨機擾動.

此處,情緒感知增量Δej(t)是t時刻個體j的速度引起的情緒變化量Δfj(v,t)及周圍行人的情緒均值Δφj(t)的相關函數,如式(3)所示.

Δej(t)=Δfj(v,t)+Δφj(t) .

(3)

該函數是情緒強度值的動態演化的關鍵,是本文的研究重點,下面對其構成開展研究.

1) 個體速度變化引起的情緒增量Δfj(v,t).在疏散過程中,若個體行走速度低于最大期望速度,他的不良情緒(煩躁、緊張、焦慮)增長較快.那么,t時刻個體j由速度引起的情緒感知增量函數如式(4)所示[12]:

(4)

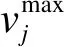
該函數可以清楚表示移動速度的變化對個體緊張情緒的波動.若實際速度遠小于最大期望速度,Δfj(v,t)值將趨近于1,即個體原地不動時,緊張情緒接近峰值.

2) 情緒感知域內他人引起的情緒增量Δφj(t).行人疏散對周圍他人情緒有認知且受其影響,文獻[4,10]定義R為情緒感知域半徑,行人j的情緒感知范圍離散化后是以該行人元胞為中心,2R為邊長的正方形.然而,文獻[12]指出,疏散個體視線內的信息傳播與非視線內信息傳播影響力存在明顯差異.據此,本文認為情緒感知域分為可視區域RV和不可視區域RI,且可視區域的情緒傳染性高于不可視區域.

t時刻個體j的情緒感知域定義為:t時刻個體j所處元胞坐標cellj(x,y)為中心,半徑為R的圓,進行元胞離散化后區域為2R邊長的正方形.

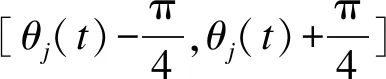
t時刻個體j的不可視感知域RI定義為:以個體j所處元胞以坐標cellj(x,y)為中心,2R為邊長的正方形中除去RV的部分,如圖2深色區域所示.

圖2 t時刻個體j的情緒感知域

個體j的情緒感知域內,情緒增量是與距離有關的函數,那么,t時刻個體元胞j感知到的他人情緒變化量函數為式(5)所示:

(5)

其中,距離權重ddk為式(6)所示:

(6)

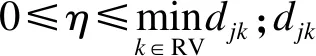
3 疏散模型

基于情緒感染的疏散模型分為情緒傳染、情緒更新和行為決策三個步驟[9],本文構建的動態情緒驅動的行人運動疏散模型以元胞自動機為基礎的行人運動模型(crowd emotional cellular automata, CECA),行人運動時因情緒狀態不同,采取不同行動策略,構成情緒驅動行為機制.該疏散模型的基本流程是:t時刻疏散個體j更新情緒強度值,情緒強度達到一定閾值后發生狀態的更新,進而改變行為策略[3，10],其過程如圖3所示.

圖3 t時刻疏散個體j一次迭代過程

3.1 情緒更新

t時刻疏散個體j疏散策略迭代過程由情緒更新判別狀態更新,執行狀態對應的疏散策略.t時刻疏散個體j緊張情緒強度值依據t-1時刻的緊張情緒強度值、行動策略、狀態、前進方向有關,受到情緒感知范圍內其他人緊張情緒強度值影響,情緒變動將引起疏散個體j狀態及行為策略的動態變化,具體狀態更新流程如圖4所示.

圖4 t時刻疏散個體j緊張情緒更新機制

3.2 狀態更新

Fu等[10]提出基于情緒閾值的狀態改變實現疏散人群狀態的動態變化.若潛在情緒狀態(S)的緊張情緒強度高于閾值λemotion時,以β概率轉成顯著情緒狀態 (I),β稱感染系數.若顯著情緒

狀態(I)的緊張情緒強度低于閾值λemotion時,以γ概率轉為潛在情緒狀態(S),γ稱平靜系數.

3.3 行為策略執行

CA行為策略是個體元胞j下一步的移動策略,個體j情緒狀態決定了j的期望速度和期望目標元胞位置,評估期望目標元胞的轉移概率,確定最終移動的目標元胞,實施移動策略.

根據個體情緒狀態定義不同的行為策略,即:

(7)

其中:ks為到出口距離影響系數；kρ為密度影響系數;cpji(t)表示t時刻疏散個體j的鄰域元胞i的狀態參數,若被占據,則該值為0,否則為1;coji(t)表示t時刻疏散個體j的鄰域元胞i是否為障礙物,若是障礙物,則該值為0，否則為1;ρji(t)表示t時刻疏散個體j的鄰域元胞i的周圍的密度.Sji(t)表示t時刻個體元胞j的鄰域元胞i到出口的最短距離.設個體j的位置坐標為C(xj,yj),鄰域元胞i的位置坐標為C(xi,yi),疏散空間中有m個有效出口,每個出口的中點坐標為C(xek,yek),則Sji(t)如式(8)所示.

(8)

4 結果與討論

將動態情緒驅動行人運動模型與經典CA模型進行比較,驗證該模型是否符合疏散時個體運動特征.在此基礎上,分析情緒強度閾值λemotion,情緒感染系數β,情緒平靜系數γ對總疏散時間的影響.

4.1 模型有效性分析

模擬的場景取文獻[12]的基礎場景,單位元胞為cl×cl,cl=0.4 m,18cl×14cl的單出口房間,出口寬度為el1=2cl.初始狀態T=0時,150位疏散個體隨機分布在空間位置上,每人占據一個元胞.疏散時間以時間步Time step為單位，用T表示，每一時間步定義為0.5 s,疏散個體移動時采用Moore鄰居規則.CECA模型的其他參數設置為:λemotion=0.6,ξ=0,β=0.5,γ=0.5.圖5和圖6分別記錄兩個模型在相同仿真場景下不同時間步的密度圖.

由圖5和圖6可以看出,隨著時間推移CECA模型與CA模型中的人流特性相同,兩種模型的行人均逐漸聚集在出口位置,在出口處表現出行人流拱形特征,但由于CA模型整體疏散較慢,其拱形特征更加明顯.在相同時間步,CECA模型中個體移動速度更快,可以表明情緒波動及感染對減少總體疏散時間是有利的,這結論與文獻[8]一致.

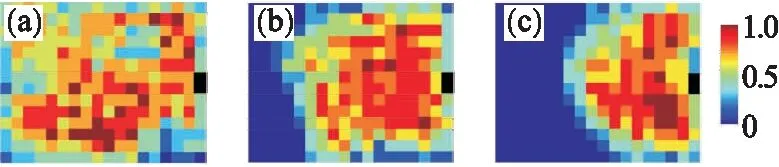
圖5 經典CA模型不同時刻人員密度圖

圖6 CECA模型不同時刻人員密度圖

為了驗證CECA模型的動態特性,在同一模擬場景下,改變情緒強度閾值λemotion,得到每一時間步的系統平均速度,如圖7所示.由圖可見,CECA模型中情緒動態變化,驅動了行為策略的動態變化,可以反映實際疏散過程中速度的動態性[1].而由于經典CA模型中的每一個行人元胞遵循同樣的規則進行同步更新,行人狀態單一,不能體現不同行人的差異化的運動特征.

圖7 系統平均速度

4.2 情緒強度閾值 λemotion的影響

文獻[10]將情緒強度閾值設定為λemotion=0.6開展了仿真實驗,然而并未討論閾值對疏散效果的影響.為了分析情緒強度閾值對總疏散時間的影響,文中模擬一個12 m×12 m的單出口房間,出口寬度為el1=3cl,設參數ξ=0,β=0.5,γ=0.5.初始人數分別為N=100,200,300,400,500時,個體隨機分布在空間中,每次仿真程序運行100次得到平均總疏散時間,結果如圖8所示.

圖8 不同情緒閾值和不同初始人數時的系統總疏散時間

由圖8所示,情緒強度閾值對系統總疏散時間是有影響的,其影響可以分為三個區間:λemotion∈[0,0.4]的疏散時間最快;λemotion∈[0.6,1]時的系統疏散時間最慢;而λemotion∈[0.4,0.6]時，是總疏散時間發生顯著變化的區間.

進一步分析情緒閾值影響疏散時間的機理,對兩類狀態群體疏散過程動態演化進行了仿真實驗.在上述同一場景中以200人為例,相同的初始位置分布和初始情緒值,情緒閾值分別取λemotion=0.3,0.5,0.7,兩類狀態群體在疏散場地內的位置如圖9所示,藍色表示S狀態個體,紅色表示I狀態個體,綠色表示出口.

情緒閾值λemotion=0.3時,個體分布如圖9a和圖 9b 所示, 初始時系統內I的人數為 155,S的人數為45,I狀態的人數多于S;T=5時系統中絕大

圖9 不同情緒閾值初始時刻和T=5時刻群體分布

多數是I狀態個體,I狀態的人數為185,S狀態的人數為2.由圖9e和圖9f可見,當λemotion=0.7時,初始時系統內S狀態的比例較大,此時S狀態的人數為156,I狀態的人數為44;而T=5時系統內絕大多數是S狀態個體,S狀態和I狀態的人數分別為183和6.λemotion=0.5時,個體分布如圖9c和圖9d所示,初始時,S狀態的人數為101,I狀態的人數為99,兩種狀態人數相當,T=5時系統中S狀態的人數為100,I狀態的人數為87,短時間內并未明顯出現哪類群體多于其他群體.

4.3 感染系數β和平靜系數γ的影響

感染系數β和平靜系數γ是疏散過程中個體情緒驅動行為改變的重要因子,主要分析其對總疏散時間的影響.以上文場景作為模擬場地,初始人數為200,考慮情緒閾值分別為λemotion=0.5和λemotion=0.6兩種情況,分別探討感染系數β和平靜系數γ單獨變化時系統中顯著情緒狀態(I)的比例,仿真程序每種情況執行100次取平均值,結果如圖10所示.

由圖10可見，γ=0.1時,λemotion=0.5,感染系數β值越大,系統中I的比例由0.5增加到1的速度越快.而λemotion=0.6時,無論β為何值時,系統中I群體的數量逐漸減少.β=0.1時,λemotion=0.5,系統中I群體比例最終都趨于1.I群體比例經過一個小幅下降后,逐步上升,特別是在T=40之后振蕩上升至1.而λemotion=0.6時,系統最終均為S群體,平靜系數γ數值越大,系統變為全S群體的速度越快.

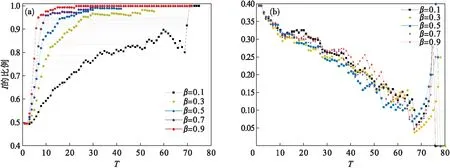
圖10 不同閾值及狀態轉移參數下的I的比例

4.4 討 論

綜合上述分析,情緒強度閾值λemotion決定了系統中兩類群體的狀態,感染系數β和平靜系數γ影響了行人之間情緒變化的速率.兩個系數可以通過外界干預調整[13-14].

λemotion≤0.5時,感染系數β影響力更大,該值越大,系統內S群體轉變成I群體的速度越快,最終達到全部都是I狀態群體,總疏散時間較少.

λemotion>0.5時,平靜系數γ影響力更大,γ越大,系統中I群體轉變為S群體的速度越快,形成全員S群體,導致疏散總時間相對較大.

上述結論為疏散管理者提供重要依據,當λemotion≤0.5,可增加感染系數β,加速行人的狀態轉化.而當λemotion>0.5時,可加速抑制平靜系數γ,使系統內群體可以盡可能向I群體轉變,對管理者來說,可以采取適當策略提高行人疏散效率.

5 結 論

1) 探討動態情緒及傳染模型,闡明情緒動態演化機理,將情緒傳染動力學與行人運動結合,構建基于動態情緒驅動的行人運動疏散模型.

2) 人員疏散運動中,情緒是重要影響因素,疏散系統中個體最終狀態由情緒閾值決定;感染系數和平靜系數影響狀態轉化速率.

3) 本研究有助于室內疏散管理者掌握疏散群體情緒動態變化趨勢,為疏散管理者了解個體情緒導致行動狀態演化機理、制定切實有效的疏散策略提供了理論依據.