基于隨機矩陣理論的配網多區域異常定位方法研究
上海電力設計院有限公司 秦嘉南
配電網具有節點眾多、運行方式靈活、設備運行環境惡劣等特點。據統計電力系統80%以上的故障都來源于配網[1]。由于配網深入城市腹地、人類活動更加頻繁,更易受到人為因素干擾,給測量裝置和電力通信設備都帶來遠超輸電網絡的影響,很多高電壓輸電側異常檢測與定位方法在配電網都難以發揮預期效果[2-3]。在現有配網故障定位研究中,對于不同類型配網異常都取得相應的檢測和定位成果,但都存在一定缺陷與不足,很少研究多區域異常的檢測與定位。
1 PMU量測數據矩陣構建與處理
1.1 原始矩陣獲取
在配網PMU量測系統中,在保持電網可觀測性的前提下,在配網中的不同位置安裝個PMU量測裝置,每個量測裝置檢測的信號維數為,PMU采樣頻率為,由PMU采集的數據通過滑動窗口的形式形成原始數據矩陣(圖1)。

圖1 滑動窗口示意圖
采樣數據矩陣的寬度反映一個矩陣中包含信息在時間上的跨度,其大小不能超過異常狀態的持續時間,假設采樣時間為,則采樣數據矩陣的寬度。根據奈奎斯特采樣定律,采樣時間不應超過故障持續時間的一半。如,配電網發生單相接地故障的持續時間為,則應滿足。本文中PMU采樣頻率設定為,則采樣數據矩陣的寬度就需滿足。滑動時間間隔會對檢測精度產生影響,越小異常檢測精度越高,單位時間內產生的矩陣數量越多,數據處理的速率也會明顯減緩,從而影響異常檢測的時效,所以的取值需在精確性和快速性上進行一定取舍。
1.2 采樣矩陣處理
2 基于高維協方差矩陣的多區域異常源數目檢測原理
2.1 高維協方差矩陣的異常檢測原理
假設矩陣YN×L為PMU量測數據經過標準化后得到的數據矩陣,此時系統正常穩定運行,矩陣為矩陣YN×L的樣本協方差矩陣,當時,根據隨機矩陣理論,用a、b表示矩陣的最大特征值和最小特征值的極限值,則有式中為噪聲的方差。

2.2 基于序貫檢測的多區域異常源檢測步驟
為實現配電網中多個異常源的檢測,假設異常源的數量為p,在上述方法中加入序貫檢測思想,進行多區域異常源的檢測。從樣本協方差矩陣中刪除前p-1行和前p-1列,其中p的取值范圍為(1,min(N,L)-1),將降階后得到的子陣分別記為。將的特征值按照降序排列,則第p個異常源的檢測統計量為:

因此第p個目標的檢測的閾值為:
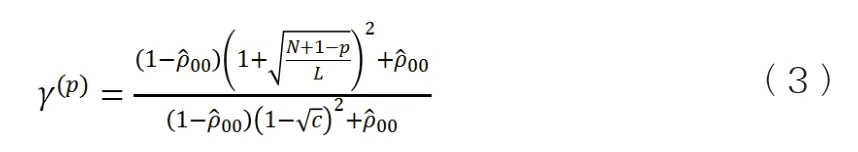
綜上,當p的取值從1開始增長到min(N,L)-1,不斷比較檢測統計量T(p)和檢測決策閾值γ(p),直到檢測統計量不再超過決策閾值為止,用公式表示即為Presult=arg max(P){T(P)〉γ(P)},從而實現多故障源數目的檢測:初始化條件,獲取隨機矩陣的協方差矩陣,并假設p=1;由式(2)和式(3)分別計算出檢測統計量T(p)和檢測閾值γ(p);比較檢測統計量和檢測閾值,判斷p第個異常源是否存在;若第p個異常源存在,則取p=p+1,在樣本協方差矩陣估計中刪除前p行和前p列、返回第二步重新計算,若第p個異常源不存在則進行下一步;檢測結束,確定故障源數目為p-1個。
3 算例分析
本文使用PSCAD軟件搭建了IEEE39標準節點的電力系統仿真模型,并根據電網可觀性進行PMU優化配置,在39節點仿真模型中配置了18個PMU量測裝置,IEEE39節點拓撲結構以及PMU節點分布如圖2所示,其中方框為PMU量測裝置。
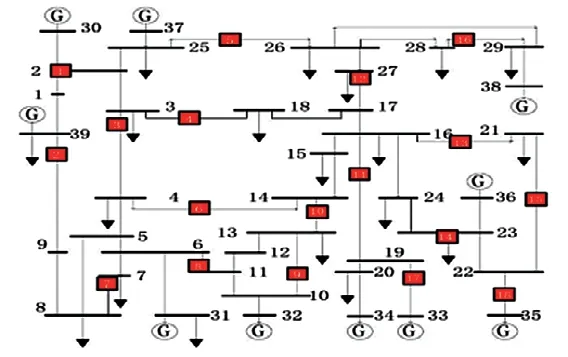
圖2 IEEE39節點及PMU分布拓撲圖
仿真模型運行環境為10kV低壓配電網,變電站均使用110kV變電站并假設為無窮大電源系統,我國低壓配電網采用中性點不接地方式,仿真模型中也將在低壓側使用中性點不接地方式,變壓器高壓側則采用經消弧線圈接地方式。本文將配電網中故障分為兩類,一類是以單相接地、單相斷線為代表的弱故障,該類故障有相對明顯的異常信號,故障持續時間也較短,故障影響范圍也較小;另一類為強擾動,通常具有持續時間長、影響范圍大的特點,如諧波超標、低頻振蕩等。
在IEEE39節點系統加入兩個三次諧波異常源,THD為5.625%超標諧波,異常持續時間為0.1s,兩個諧波源的位置分別為IEEE39節點拓撲中母線16與母線21之間的LN23、母線4與母線14之間的LN8。當仿真時長達到1s時,位于母線16至21之間以及母線4至14之間的兩個三次諧波源接入仿真電路,基于序貫檢測后將本算例中T、T(2)、T(3)及其對應閾值的仿真數據繪制成圖3、并可觀察到:樣本矩陣和一階子矩陣的檢測統計量都超過了閾值,而二階子矩陣未超過閾值,說明當去除前兩個異常源后二階子矩陣已不呈現異常狀態,從而可判斷此時配電網存在兩個異常源。

圖3 樣本協方差矩陣的檢驗統計量
利用主成分分析法進行故障定位,選取故障發生前4個與故障發生后6個等間隔的滑動窗口,并取用于重構數據的主成分數量為2、即k=2,計算其各個PMU量測變量對主成分的因子載荷,并通過得分進行排序。當故障發生后主成分累計貢獻率有顯著提升。故障發生前PMU各量測值的得分排序也是隨機分布的;而故障發生后,本例中位于樣本矩陣的61、49、68、45列的數據得分明顯上升。經PSCAD軟件的目錄檢索,故障發生后得分上升明顯的信息量來自于6號PMU、13號PMU等。
將故障發生后滑動窗口構建的共計200個樣本矩陣進行整理,將得分排序前10的PMU在這200個滑動窗口中的出現頻次進行統計,再將故障發生時各PMU在得分體系下的得分整理,其中前六名的PMU編號、計數(次)、比率(%)、得分分別為6/200/100/1.548、13/200/100/1.541、12/197/98.5/0.858、9/171/85.5/0.845、1/166/83 /0.847、3/152/76/0.672,由此可知6號、13號、12號PMU出現的頻次最高,6號和13號PMU得分遠高于其他PMU。說明其在故障后長時間、高相關性地影響著協方差矩陣的主成分,從而可以判定6號和13號PMU量測裝置的位置最接近異常點。因此在該仿真環境下配電網中共有2個故障源,故6號和13號PMU即為故障源定位結果,與仿真設置值一致,驗證了本文提出基于隨機矩陣理論的配網多區域異常定位方法的有效性和針對不同類型故障的通用性。

