基于反向傳播人工神經網絡對SiC氧化反應行為的預測研究

趙春陽，王恩會，方 志，郭春雨，段興駿，侯新梅

(北京科技大學鋼鐵共性技術協同創新中心，北京 100083)

0 引 言

非氧化物材料因其強度高，具有良好的抗氧化、抗熱震和抗腐蝕性能，被廣泛應用于冶金、電力和化工等行業[1-3]。在實際服役條件下，作為高溫設備內襯耐火材料重要組成的非氧化物材料其本身的氧化行為易導致相應耐火材料高溫性能不斷惡化，進而降低服役壽命。因此明晰非氧化物材料在高溫服役過程中的反應行為對相應耐火材料服役壽命的預測和優化設計尤為重要[2-5]。

在非氧化物材料高溫服役過程的反應行為研究方面，由于高溫反應的復雜性及實驗條件的苛刻性，反應數據準確獲取困難且重現性差，而現有的測試僅考慮單一因素，與材料實際服役條件相距甚遠。除了實驗手段外，多采用動力學模型進行分析[5-8]，但是動力學模型的建立往往都需要進行大量數據處理，當遇到不同的反應機理時不可避免地需要更多的表達式來描述反應行為，且很難同時滿足描述準確性高和模型參數簡單兩個條件，實際應用效果不佳[9-12]。

隨著人工智能的快速發展和大數據技術在材料領域的應用探索，越來越多的機器學習算法被用于解決材料制備和性能等方面的研究。人工神經網絡(artificial neural network， ANN)是基于簡單處理元素(神經元)組成的相互連接的并行系統，該系統利用已有數據學習輸入和輸出之間的函數關系，而無需事先假設輸入與輸出關系，具有自學習功能和高速尋找優化解的能力。因此，ANN在復雜系統的實際應用中具有強大的優勢[13-15]。反向傳播(back propagation， BP)學習算法是一種按照誤差逆向傳播訓練多層前反饋神經網絡的算法，通過輸出層得到輸出結果和期望輸出的誤差間接調整各層之間的權值，從而達到優化網絡的目的。ANN與BP的結合在解決非線性回歸問題方面有巨大潛力[16-17]，有望更好地認知非氧化物材料在高溫服役過程的反應行為。

本文以典型非氧化物材料SiC為例，將BP-ANN應用于描述其氧化行為，建立精度較高的人工神經網絡模型，為非氧化物材料的氧化行為和對應耐火材料的優化設計研究提供新思路和新途徑。

1 實驗數據獲取與BP-ANN模型開發

神經網絡模型的建立是基于對已有數據輸入與輸出關系的不斷學習來實現的。訓練網絡用到的SiC氧化實驗數據是筆者課題組之前試驗獲得的[18]和補充的不同水蒸氣體積分數條件下的氧化數據，如圖1所示(圖中Δm為粉末質量變化量，m0為粉末初始質量)。

圖1 不同條件下SiC質量增益分數隨時間變化曲線Fig.1 Curves of SiC mass gain percentage with time under different conditions

在本文中，使用了由輸入層、隱藏層和輸出層組成的三層標準反向傳播神經網絡。反向傳播是一種計算非線性多層網絡梯度的方法。在早期的標準算法中，隨機初始賦予神經網絡一組權值，然后根據輸入數據調整權值，使輸出誤差達到最小[19]。但這種算法效率低下，而且不可靠，因為需要大量的迭代才能收斂。因此，標準算法的許多變體被開發出來，其中Levenberg-Marquardt是最受歡迎也是速度最快的算法[20]。所以，本文采用Levenberg-Marquardt算法進行BP-ANN訓練，采用mapminmax函數進行數據歸一化處理，采用歸一化均方誤差性能函數(mean squared error， MSE)進行系統誤差性能函數修正。

用于網絡訓練的數據是在熱重分析儀上完成的，其輸出值的x軸為時間，y軸為質量變化率。在熱重測試中，能夠影響最終結果的因素只有兩個，即氧化時間和氧化溫度，本文將這二者作為輸入值，將樣品的質量變化率作為輸出值，進行BP-ANN訓練。一個好的神經網絡建模過程中，不僅要保證誤差較小，相關性較好，而且要對訓練集以外的樣本有較強的預測能力。為盡量保證所建模型的可靠性，在空氣環境的數據除1 300 ℃以外其他4個溫度下的氧化數據中均勻取50個數據點作為訓練集，1 300 ℃中的50個氧化數據點作為預測樣本集，用于驗證網絡預測的有效性。在不同水蒸氣體積分數環境的實驗數據中，將Ar+10%H2O條件下1 300 ℃和文獻[18]中Ar+20%H2O條件下1 200 ℃的數據作為預測樣本集，其余作為訓練集。所有輸入數據都在訓練前進行歸一化處理，用于描述SiC的氧化行為的BP-ANN結構如圖2所示，圖中h1～hn表示隱藏層的神經元，具體的神經元個數將在本文后續進行討論。

圖2 BP-ANN結構Fig.2 BP-ANN structure

2 結果與討論

2.1 BP-ANN擬合預測SiC的氧化行為

隱藏層神經元的多少直接影響BP-ANN的預測能力，神經元過少將不足以表達系統的復雜非線性關系，神經元過多則會導致過擬合造成網絡泛化能力下降。從網絡精度和泛化能力綜合考慮，將隱藏層神經元的數量從5～14進行調整，觀察BP-ANN的預測結果精度變化，從中選擇最佳精度。預測結果的誤差隨神經元數量的變化如圖3所示。

通過圖3可以看出，當隱藏層的神經元為9個時，BP-ANN的預測數據與實驗數據的相對誤差僅為2.83%，所以接下來將用神經元數量為2-9-1的神經網絡模型對數據進行訓練，該神經網絡的訓練次數為1 000次，學習效率為0.01。

用訓練好的BP-ANN對1 300 ℃時SiC的氧化行為進行預測，其預測值與實驗數據比較如圖4所示。可以發現，預測結果與實驗結果的誤差為2.83%，說明了該模型的可靠性。廣泛用于描述SiC氧化行為的動力學模型雖參數意義明確，但其公式較為復雜且前期需要進行大量的數據處理工作。相比之下BP-ANN的模型更為簡單，僅需要將獲得的熱重曲線輸入到模型中，運行該模型，即可預測某一溫度下的SiC氧化行為，這證明了BP-ANN在預測非氧化物材料方面具有良好的應用前景。

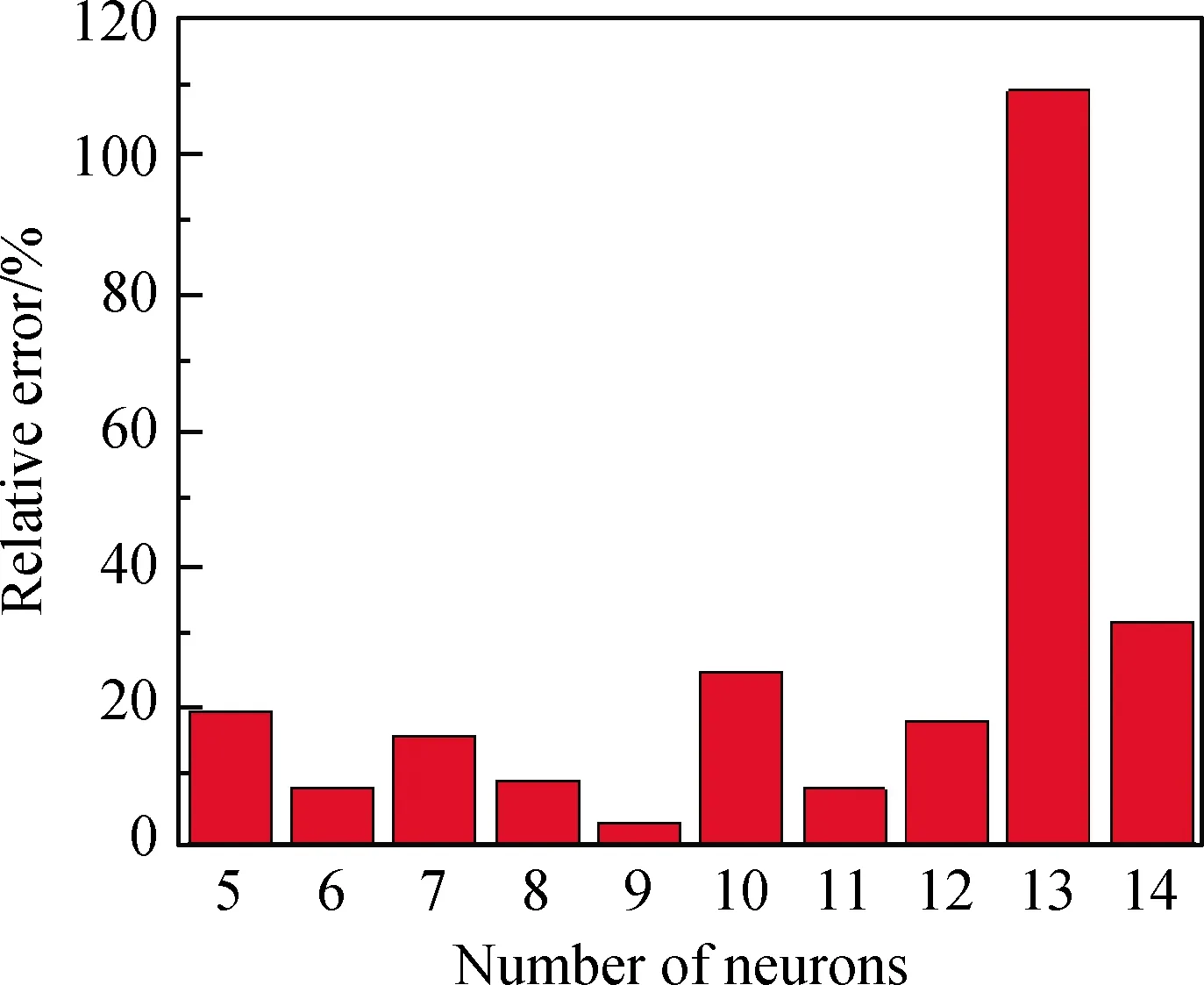
圖3 隱藏層含有5～14個神經元時的預測數據與 實驗數據的相對誤差Fig.3 Relative errors of predicted data and experimental data when the hidden layer contains 5～14 neurons

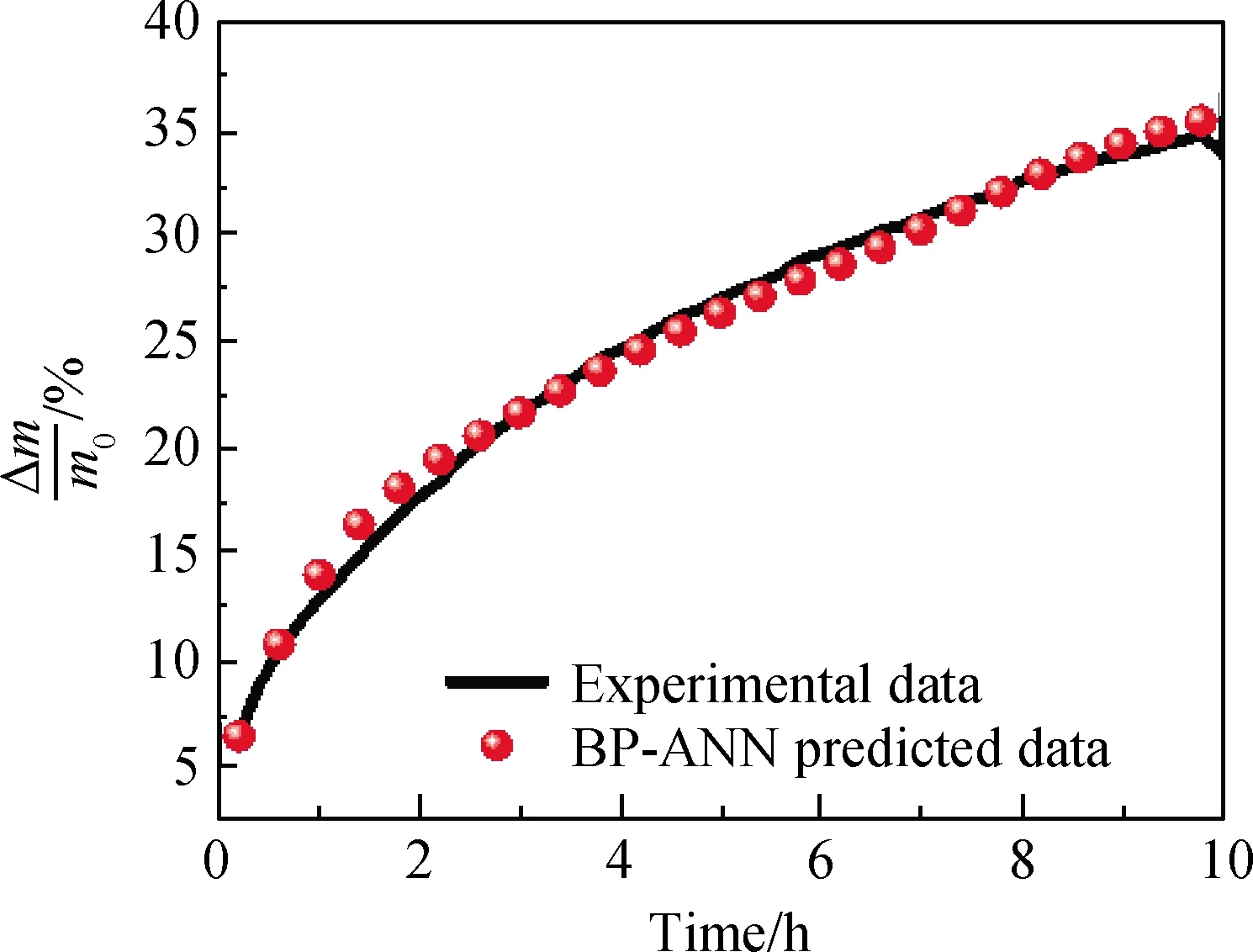
圖4 SiC質量增益分數隨時間變化曲線Fig.4 Curve of SiC mass gain percentage with time

圖5 隱藏層含有3～12個神經元時的預測數據與 實驗數據的相對誤差Fig.5 Relative errors of predicted data and experimental data when the hidden layer contains 3～12 neurons

BP-ANN除了能夠預測不同溫度的SiC氧化行為，還可以對某一特定溫度下長時間的氧化行為進行預測。本文將SiC在空氣中1 400 ℃條件下1～8 h的氧化數據作為訓練集，8～10 h作為預測樣本集。預測結果的相對誤差隨神經元的變化如圖5所示。

通過圖5可以看出，當隱藏層的神經元為5個時，BP-ANN的預測數據與實驗數據的相對誤差僅為2.87%，所以接下來將用神經元數量為2-5-1的神經網絡模型對數據進行訓練，該神經網絡的訓練次數為1 000次，學習效率為0.01。用訓練好的BP-ANN對1 400 ℃下8～10 h的SiC的氧化行為進行預測，其預測值與實驗數據的比較結果如圖6所示。計算表明，預測結果與實驗結果相對誤差為2.87%，進一步說明了該模型的可靠性，也體現了該模型在預測SiC等相關非氧化物材料服役壽命方面的可行性。

圖6 SiC質量增益分數隨時間變化曲線Fig.6 Curve of SiC mass gain percentage with time

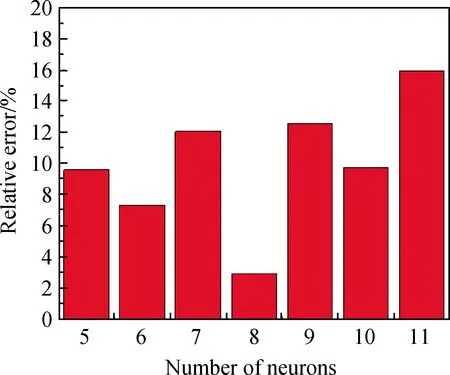
圖7 隱藏層含有5～11個神經元時的預測數據與 實驗數據的相對誤差Fig.7 Relative errors of predicted data and experimental data when the hidden layer contains 5～11 neurons

為了能夠進一步體現BP-ANN對于復雜非線性數據的擬合優勢，將具有水蒸氣體積分數、溫度、時間三個因素的數據輸入BP-ANN進行訓練，驗證其預測效果。同樣地，首先進行神經元選擇，測試不同神經元個數對預測數據與實驗數據之間相對誤差的影響，結果如圖7所示。因為當神經元個數調整至12個時，神經網絡已經過擬合，故不再進行測試。

通過圖7可以看出，當隱藏層的神經元為8個時，BP-ANN的預測數據與實驗數據的相對誤差僅為2.94%，所以接下來將用神經元數量為3-8-1的神經網絡模型對數據進行訓練，該神經網絡的訓練次數為1 000次，學習效率為0.01。用訓練好的BP-ANN對SiC在Ar+10%H2O條件下1 300 ℃、Ar+15%H2O條件下1 200 ℃和Ar+20%H2O條件下1 200 ℃的氧化行為進行預測，其預測值與實驗數據比較如圖8所示。計算表明，預測結果與實驗結果的相對誤差為2.94%。由上可見，在三個甚至更多影響因素的情況下，BP-ANN仍具有出色的預測能力，且其操作簡單,誤差較小，在描述非氧化物材料復雜的高溫反應行為方面具有特定優勢。

圖8 不同條件下SiC質量增益分數隨時間變化曲線Fig.8 Curves of SiC mass gain percentage with time under different conditions

2.2 使用BP-ANN模型輸出計算反應活化能和反應速率常數

建立氧化動力學模型是研究氧化行為、認識氧化規律的重要手段，氧化過程的反應活化能、反應速率常數都是氧化動力學模型中的重要參數。為進一步驗證BP-ANN對氧化行為描述的準確性，通過對神經網絡預測的結果進行回歸，可以得到對應的反應活化能。神經網絡預測結果計算的反應活化能和反應速率常數與實驗數據擬合回歸得到的數據對比分別如表1和表2所示。

表1 實驗數據與BP-ANN預測數據計算的反應活化能Table 1 Reaction activation energy calculated from experimental data and neural network predicted data

表2 實驗數據與BP-ANN預測數據計算的反應速率常數Table 2 Reaction rate constant calculated from experimental data and neural network predicted data

在表1和表2中可以清晰地看到:BP-ANN預測數據計算的反應活化能與實驗數據計算的反應活化能相差不大，相對誤差最大為1.98%；預測數據計算的反應速率常數與實驗數據計算的反應速率常數的相對誤差最大僅為3.56%，均在誤差允許的范圍內。結合預測數據的準確性，表明BP-ANN具有描述整體氧化行為和確定動力學參數的能力，在研究非氧化物材料氧化行為方面應用前景廣闊。

3 結 論

(1)SiC作為非氧化物材料的典型代表，是耐火材料的重要組成部分，對其氧化行為的研究尤為重要。通過隱藏層神經元個數的精度測試，本文建立了不同神經元個數的BP-ANN，用于預測不同反應環境下SiC的氧化行為。

(2)通過網絡訓練，BP-ANN預測SiC的氧化數據與實驗數據的相對誤差均低于3%，這種方法可以解決之前氧化模型無法兼顧描述準確性和參數簡單的問題，而且在處理多元非線性數據時具有出色的結果，僅需將SiC的氧化數據輸入模型后訓練、預測即可。

(3)將BP-ANN預測數據回歸計算得到的氧化反應活化能和反應速率常數與實驗數據回歸計算的相比，相對誤差不超過4%。這表明該BP-ANN不僅可以描述氧化行為，還可以確定氧化動力學參數，在研究非氧化物材料氧化行為和設計對應耐火材料方面應用前景廣闊。