端鉤型鋼纖維UHPC抗壓強度的試驗研究

常亞峰，師俊平，侯亞鵬

(1.陜西省建筑科學研究院有限公司，西安 710082；2西安理工大學土木建筑工程學院，西安 710048)

0 引 言

隨著超高性能混凝土(ultra high performance concrete，UHPC)中摻雜的鋼纖維體積含量增加，會對其基體形成一定的約束作用[1]，可有效延緩UHPC基體的開裂，從而UHPC試件的破壞過程、破壞形態以及壓縮耗能等發生變化。鋼纖維的外形及摻量對UHPC的抗拉強度有顯著的影響[2]，鋼纖維體積摻量[3-8]一般不超過3%。UHPC在荷載作用下的破壞模式基本為纖維的拔出，端鉤型鋼纖維的外形構造可提供較大的抗拔脫力[4,9]。當UHPC基體中鋼纖維體積摻量為2%時，其在基體中黏結性能最強[9-11]，鋼纖維的增強、增韌[12]作用充分發揮。當鋼纖維體積摻量從2%增至3%時，UHPC的抗壓強度[13-14]增加幅度較小；當鋼纖維體積摻量由3.5%增至5.0%時，UHPC抗壓強度反而減小[14]。纖維體積摻量在3%以內時，隨著纖維體積摻量的提高，超高性能混凝土抗壓強度逐漸增大；鋼纖維的摻入對UHPC的壓縮延性提高幅度顯著。

素混凝土立方體試件軸心受壓時，在試件中部非約束區域率先膨脹，試件突然崩裂破壞并射出試件碎塊[15]。對UHPC而言，特別是摻入端鉤型鋼纖維的UHPC，其基體中骨料最大粒徑僅為1～2 mm，長度為12 mm的端鉤型鋼纖維對UHPC的延性影響較大。由于鋼纖維兩端折鉤[9]的構造，極大地提高了纖維與基體之間的握裹力與抗拔脫力，延緩基體內微裂紋的擴展，改變了其擴展方向，提高了UHPC材料的峰值荷載和壓縮耗能，澆筑時端鉤型纖維不易沉底，在基體高度方向分散較均勻，性價比較高。由于UHPC的骨料最大粒徑為普通混凝土石子的1/10，端鉤型鋼纖維長度是其最大骨料粒徑的6～13倍，對UHPC基體的約束效果明顯增加，進而影響UHPC立方體試件的受壓荷載-位移曲線。

目前對UHPC立方體試件的研究大多為試驗配合比和峰值受壓荷載，而針對端鉤型纖維體積摻量及不同尺寸對UHPC立方體試件抗壓強度的影響和抗壓破壞形態的研究較少，因此對摻雜端鉤型鋼纖維的UHPC立方體試件的抗壓性能研究十分必要。本文制作了5組24個不同纖維體積摻量的UHPC立方體試件，對其進行單軸受壓試驗，觀測其破壞過程和破壞形態，采集了UHPC試件加載過程中的荷載、變形等數據，得出UHPC的試件的荷載-位移試驗曲線。分析不同纖維體積摻量及不同尺寸對UHPC試件的破壞過程、破壞形態和抗壓強度的影響，建立不同纖維體積摻量的UHPC試件的抗壓強度和其對應的峰值位移的預測模型。

1 實 驗

1.1 原材料

試驗采用5種原材料：水泥為P·O 52.5R普通硅酸鹽水泥；硅灰為無定形超細(非晶體)粉末，灰白色，比表面積為19 m2/g，SiO2質量分數≥93%，燒失量≤2.6%；石英砂選擇SiO2質量分數大于99.72%，Fe2O3質量分數為0.024%的白色石英砂，由0.85～2.00 mm、0.425～0.85 mm、0.212～0.425 mm、0.125～0.212 mm和0.062 mm等5種組成；減水劑采用聚羧酸高效減水劑；水采用市政自來水；纖維采用端鉤型鋼纖維(見表1)，本試驗所用鋼纖維端鉤采用兩次135°彎折而成，如圖1所示。

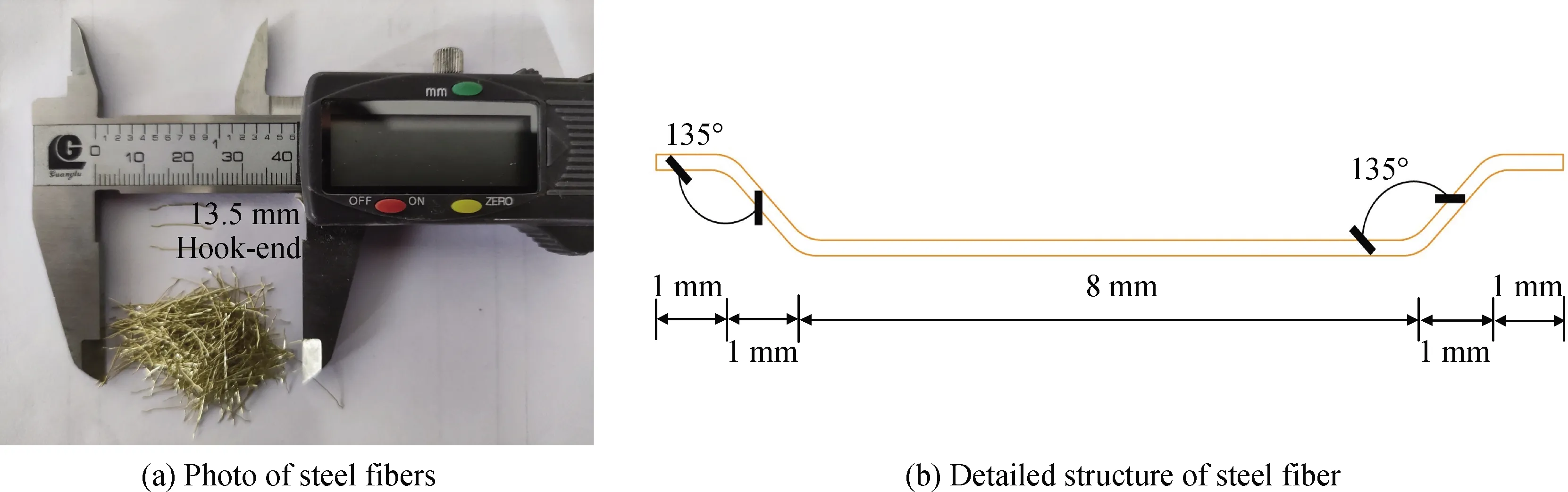
圖1 試驗用鋼纖維Fig.1 Steel fibers used in the test

表1 鋼纖維性能指標Table 1 Properties of steel fiber

1.2 配合比

本文基于文獻[16-17]中得到UHPC基體的最優配合比，以端鉤型鋼纖維體積摻量為試驗變量，對立方體試件進行抗壓試驗，纖維體積摻量為0%～3%，共計5組試驗，考察纖維體積摻量對UHPC材料立方體試件受壓性能的影響，試驗配合比見表2，其中5組不同的鋼纖維體積含量分別為0%、0.5%、1%、2%、3%，對應的編號為UHPC 1～5。

表2 UHPC材料配合質量比Table 2 UHPC material mix mass ratio

依據《活性粉末混凝土》GB/T 31387—2015[18]中第9.3條，纖維長度小于40 mm，UHPC 1～5組抗壓強度應選用100 mm×100 mm×100 mm的立方體試件，每組制作3個。為研究尺寸的影響，UHPC 3～5組另制作200 mm×200 mm×200 mm的立方體試件，每組制作3個。共計24個試樣。

1.3 試件的制作及養護

試驗采用HJW-60型單軸混凝土攪拌機制備UHPC拌合物，經過多次試驗后確定其拌和過程如下：

(1)將水泥、硅灰、石英砂投入攪拌機中干拌2 min，使其混合均勻;

(2)將95%的水、95%的減水劑緩慢加入攪拌機中拌和5 min，將UHPC基體攪拌為流動狀態;

(3)用鋼纖維分散器將端鉤形鋼纖維投入攪拌機中，使鋼纖維在UHPC基體中均勻分散;

(4)將剩余5%的水、5%的減水劑加入攪拌機中拌和2 min，以改善UHPC的工作性能。

將端鉤形鋼纖維/UHPC拌合物裝入立方體試模中，放置在振動臺上振動2 min，振動頻率為50 Hz/s，之后用抹刀將模具上表面多余部分抹掉并壓平。

將制作好的試件放入標準養護箱(溫度為(20±5) ℃，相對濕度≥95%)內養護24 h后拆模，之后繼續放入養護箱養護至28 d齡期后，取出進行試驗。

1.4 試驗加載及量測

試驗加載在西安理工大學的5 000 kN微機控制電液壓伺服試驗機上進行(見圖2)。依據文獻[19]和《普通混凝土力學性能試驗方法標準》GB/T 50081—2002[15]，測定立方體抗壓強度的試驗過程應連續均勻地加荷，加載速率為1.2 MPa/s。試件壓縮位移由布置在加載底座上的位移計(見圖2(a))測定，試件的豎向荷載由加載裝置直接量測。

圖2 試驗加載裝置Fig.2 Test loading equipment

2 測試結果

2.1 素UHPC試件破壞現象及破壞形態

對試件UHPC 1-100(鋼纖維體積摻量為0%)，在整個加載過程中未發現試件外觀異常和受壓異響，隨著試件受荷的繼續增加，當試件受荷臨近峰值荷載時，試件表面出現裂紋，試件45°斜向貫通斷裂面急速形成，最終發出“嘣”一聲巨響，試件碎塊崩散在加載裝置的周圍，少量崩落碎渣彈出2 m左右。由于試件制作比較平整，加載面上端板采用球支座自動調平，試件最終呈現出理想的“錐形”脆性破壞，但試件外觀破壞嚴重，如圖3(a)所示。

圖3 試件典型破壞形態Fig.3 Typical failure patterns of specimens

2.2 纖維約束UHPC試件破壞現象及破壞形態

對試件UHPC 2～5(鋼纖維體積摻量0.5%～3%)纖維約束試件，與未摻纖維試件類似，在加載初期未見試件外觀異常和受壓異響，此時基體與纖維黏結界面處于彈性變形階段，基體與纖維等量協調變形，微裂紋的萌生、擴展極其微弱，可以忽略，基體與纖維同時等量變形，試件表面未發現裂紋。

圖4 UHPC基體斷裂面處纖維Fig.4 Fiber at the fracture surface of UHPC matrix

在纖維約束UHPC試件受荷達到峰值荷載的40%左右時，即試件UHPC 2-100、試件UHPC 3-100、試件UHPC 4-100和試件UHPC 5-100受荷分別達40 MPa、45 MPa、50 MPa和60 MPa時，試件斷續發出“嗞嗞”聲，但未發現試件表面宏觀開裂現象。這是由于試件體內石英砂與膠凝材料(水泥和硅灰)結合面開始產生橫向拉應變而損傷，損傷處的纖維與基體發生相對滑移，端鉤型纖維抑制了損傷的擴展速度。在受荷達到臨近峰值荷載時，即試件UHPC 2-100、試件UHPC 3-100、試件UHPC 4-100和試件UHPC 5-100受荷分別達96 MPa、100 MPa、110 MPa和125 MPa時，試件發出的“噼啪”聲變快變強，其表面產生肉眼可見的豎向裂縫。這是因為在試件產生明顯橫向膨脹，導致UHPC基體斷裂而使試件產生表觀裂縫。隨著荷載的繼續增大，纖維的約束作用改變了斜向主裂紋的擴展方向，在試件體內形成斜向貫通斷裂面。隨著纖維摻量的增加，破壞裂縫與豎直線的夾角越小，說明纖維摻量對軸壓作用下橫向拉應變的約束作用越強。當試件達到峰值荷載時，斷裂面處纖維未斷裂(見圖4)，其發出“嘭”一聲巨響而宣告破壞，這是因為形成貫通斷裂面而失去承載力。纖維約束試件破壞后，發現少量崩落碎屑散落在試件周圍，試件UHPC 2-100、試件UHPC 3-100、試件UHPC 4-100和試件UHPC 5-100的最遠碎屑崩射距離分別為0.3 m、0.2 m、0.15 m和0.08 m，隨著纖維摻量的增加，破壞時碎屑崩射距離變小。由于垂直于裂縫鋼纖維的橋連作用，試件UHPC 2～5破壞后未完全碎裂，同時試件UHPC 2-100、試件UHPC 3-100、試件UHPC 4-100和試件UHPC 5-100的最大裂縫寬度分別為4 mm、3 mm、1 mm和0.4 mm，隨著纖維摻量的增加，破壞時產生的最大裂縫寬度變小。

試件UHPC 3-200、試件UHPC 4-200和試件UHPC 5-200的破壞過程與其相應的100 mm立方體試件的破壞過程基本一致，試件破壞后，其最遠碎屑崩射距離分別為0.25 m、0.18 m和0.10 m，其最大裂縫寬度分別為2 mm、0.8 mm和0.3 mm。

試件UHPC 2～5，其最終破壞呈現多條豎向裂縫，這是由于鋼纖維的存在抑制了試件受壓時錐形滑裂面的形成。隨著纖維摻量的增大，試件破壞時產生的豎向裂紋數量變少，裂縫寬度變小，破壞時的完整形態變強。最終破壞時試件未碎裂，呈現“壞而不碎”的破壞形態，如圖3(b)～(h)所示。

2.3 荷載-位移曲線

圖5(a)為試驗實測5組的15個100 mm立方體UHPC試件的平均荷載-位移曲線。由圖5(a)可知，隨著纖維摻量的增大，曲線的斜率逐漸增大，即試件的剛度逐漸增大。UHPC試件受壓峰值荷載(Fmax)、相應的峰值位移(δmax)和試件極限壓縮變形(δu)均隨纖維摻量的增大而逐漸增加，這是由于當試件裂紋出現后，鋼纖維的橋連作用使UHPC基體處于約束狀態，并且鋼纖維端鉤的存在，極大地提升了纖維與UHPC基體的抗拔脫力，增強了其約束效應，進而提高了UHPC的壓縮剛度、抗壓強度和破壞后整體性等。與未摻鋼纖維組相比，隨著摻入纖維摻量的增大，曲線下降段的坡度減緩，并且下降段坡度差異較小，這是由于鋼纖維對UHPC試件曲線下降段的約束作用較小。

圖5 各試件受壓應力-應變關系曲線Fig.5 Stress-strain curves of specimens

圖5(b)為試驗實測3組9個200 mm立方體UHPC試件的平均荷載-位移曲線。由圖5(b)可知，當試件尺寸增大至2倍時，隨著纖維摻量的增加，荷載-位移曲線上升段的斜率越來越大，且差異更明顯。試件的峰值荷載(Fmax)、相應的峰值位移(δmax)和試件極限壓縮變形(δu)與100 mm試件變化結果類似，但相應的峰值荷載差異較大，隨著纖維摻量的增大，曲線下降段坡度差異較大，這說明隨著試件尺寸的增大，鋼纖維對UHPC試件曲線下降段的約束作用較大。

表3為各組試件受壓力學參數的試驗結果。

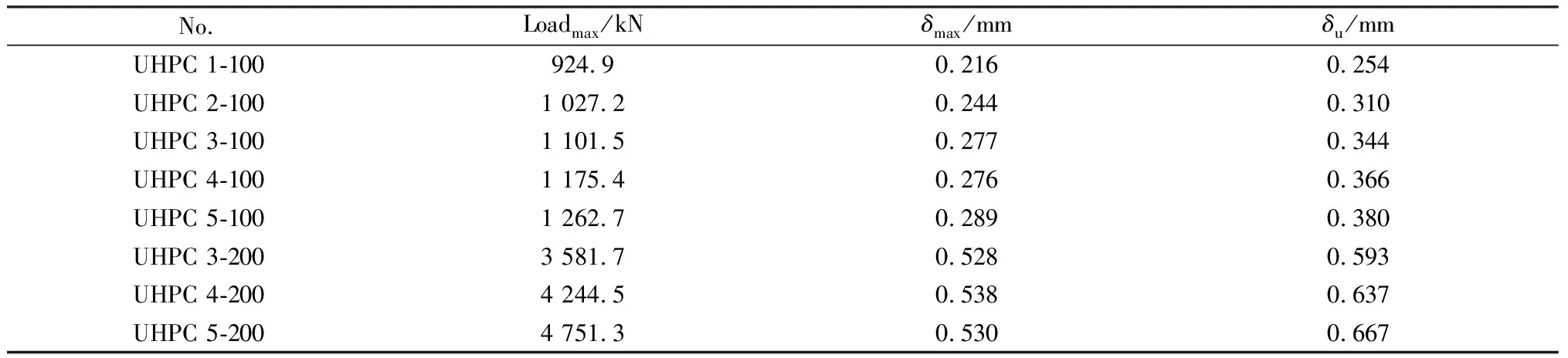
表3 抗壓強度試驗結果Table 3 Test results of compressive strength

3 結果分析

3.1 纖維約束系數

由試驗結果可知，纖維增強混凝土需考慮纖維約束系數Ωf對其受壓性能的影響。參照規程[2]，纖維約束系數受纖維品種、纖維的外形、纖維長徑比等參數的影響，即

(1)

式中：αc為纖維種類對約束纖維混凝土的影響指數，端鉤型取1.0，圓柱直線形取0.95；Vf為纖維體積摻量；lf為纖維長度，單位為mm；df為纖維直徑，單位為mm。

本文涉及的各組試件的纖維約束指數，見表4。

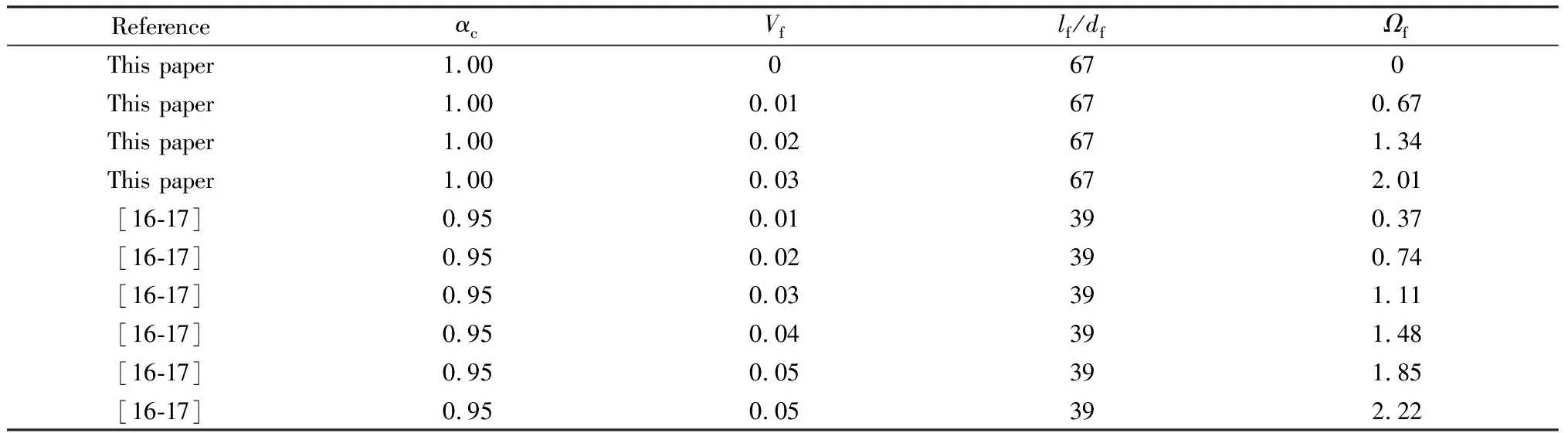
表4 纖維約束指數Table 4 Fiber constraint index

3.2 纖維約束系數對初始損傷強度的影響

纖維約束系數與初始損傷對應的強度(fD0)的關系如圖6所示。由圖6可知，隨著纖維約束指數的增加，UHPC試件的初始損傷對應的強度基本呈線性關系增長。這是因為試件的均勻損傷過程中，跨越損傷裂紋的纖維可以有效緩解試件的損傷，隨著纖維約束指數的增加，跨越損傷裂紋的纖維數量基本呈線性關系增多，對單軸壓縮時產生的側向拉應變延緩作用增強，導致UHPC試件較遲出現損傷局部化現象。

3.3 纖維約束系數對立方體抗壓強度的影響

纖維約束系數對試件抗壓強度的影響如圖7所示。從圖中可以看出：隨著纖維約束系數的增大，UHPC試件的抗壓強度有所增長。與未摻纖維組相比，纖維約束系數從0.335增加至2.010，立方體抗壓強度分別提高至素UHPC試件的1.11倍、1.19倍、1.27倍和1.37倍。當纖維體積摻量為3%時，試件立方體抗壓強度增加37%。這是由于UHPC立方體試件在豎向荷載作用下發生了橫向變形，橫向拉應力引起試件沿豎向開裂(見圖4)。隨著纖維約束系數的增加，立方體試件沿豎向開裂越顯著，且隨著纖維約束系數的增加，抑制豎向裂縫的纖維約束作用增強，產生的跨裂縫纖維橋接力增大，故纖維體積摻量不超過3%時，UHPC試件的抗壓強度隨纖維約束系數的增加而增大。

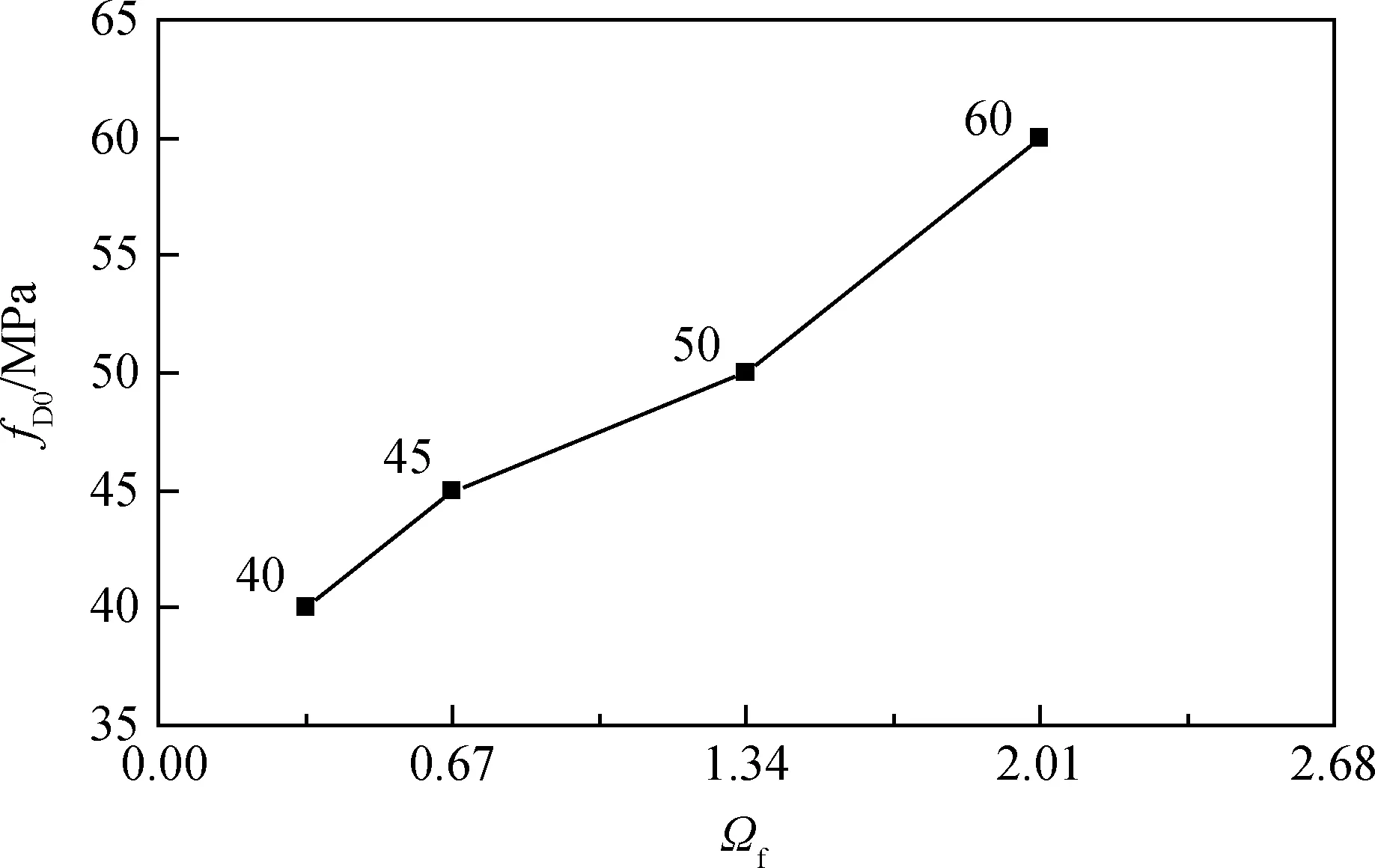
圖6 試件初始損傷對應的強度與纖維約束指數的關系Fig.6 Initial damage strength and fiber constraint index of specimens

圖7 各試件立方體抗壓強度與纖維約束系數的關系Fig.7 Relationship between cube compressive strength and fiber constraint index of specimens

3.4 纖維約束系數對峰值位移的影響

圖8為纖維約束系數對UHPC立方體試件峰值荷載相對應的峰值位移的關系圖。由圖8可知，纖維約束系數對其峰值位移有顯著影響，端鉤型鋼纖維約束系數不超過2.010時，隨著纖維約束指數的增加，峰值位移逐漸增大。與未摻纖維組相比，纖維約束系數從0.335逐漸增加至2.010時，峰值位移分別增加至素UHPC立方體試件的1.13倍、1.28倍、1.28倍和1.34倍。當纖維體積摻量為3%時，試件立方體抗壓峰值位移增加34%。增長速率逐漸增大，說明端鉤型纖維體積摻量在0.5%～3%，鋼纖維在UHPC基體中分散較均勻，未出現纖維沉底和結團削弱效應。

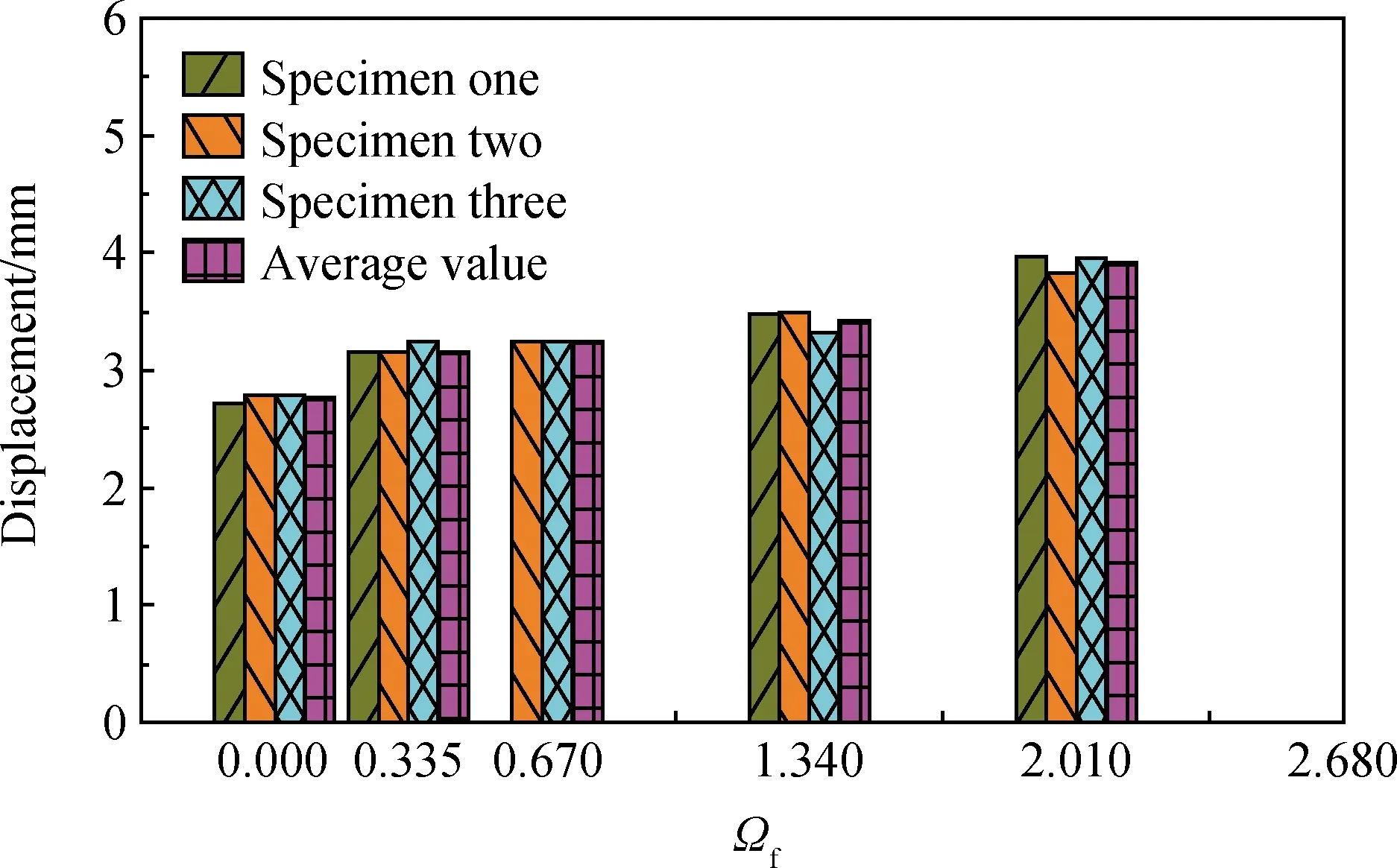
圖8 各試件峰值荷載位移與纖維約束指數的關系Fig.8 Relationship between peak load displacement and fiber constraint index specimens

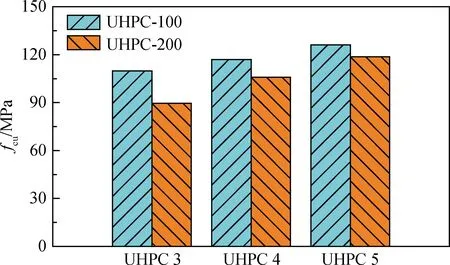
圖9 不同尺寸與抗壓強度的關系Fig.9 Relationship between different sizes and compressive strength of cube specimens

3.5 尺寸效應對抗壓強度的影響

圖9為不同尺寸與UHPC抗壓強度的關系，由圖9可知，試件尺寸相同時，隨著纖維摻量的增加，兩種尺寸的UHPC抗壓強度均逐漸增大；纖維摻量相同時，隨著試件尺寸的增大，UHPC的立方體抗壓強度均降低；UHPC 3-200、UHPC 4-200、UHPC 5-200的抗壓強度分為其相應纖維摻量的UHPC 3-100、UHPC 4-100、UHPC 5-100的81.5%、84.0%、94.1%，說明尺寸效應對UHPC試件的影響較顯著，隨著纖維摻量的增大，尺寸效應對UHPC的影響逐漸減小，尤其當纖維摻量為3%時，200 mm的立方體試件的抗壓強度可達其100 mm立方體試件的94.1%。

3.6 纖維約束系數對壓縮耗能的影響

參照標準[2]，根據纖維約束UHPC立方體試件的軸壓荷載-變形全曲線計算的壓縮耗能Wi、軸壓韌性比Ri隨纖維約束系數的變化見表5。

(2)

(3)

式中：Fmax為荷載-位移曲線的荷載峰值；δ0.85為下降至0.85倍荷載峰值時相應的壓縮位移;i為不同纖維摻量的組別。

由表5可知，與未摻纖維UHPC組相比，纖維約束指數對壓縮耗能的影響顯著，纖維約束系數為0.335、0.670、1.340和2.010時，UHPC的壓縮耗能分別增加了35%、69%、86%和110%，這是因為此時的纖維數量，使纖維周圍的100 mm的立方體UHPC基體得到了有效的約束，受荷時引起纖維與基體之間有效共同受力，跨越斷裂面的纖維延緩了主裂紋的擴展。纖維約束系數為0.335、0.670、1.340和2.010時，UHPC的軸壓韌性比分別增加3%、8%、15%和9%，隨著纖維約束指數的增加，其軸壓韌性比呈先增大后減小趨勢。鋼纖維摻量從1%增至3%時，UHPC的壓縮耗能僅增加23.9%；同時軸壓韌性比在纖維體積摻量2%時，最大可達0.601。因此，端鉤型鋼纖維摻量在2%時性價比最佳。與100 mm立方體UHPC試件相比，尺寸增大一倍的試件UHPC 3-200、UHPC 4-200、UHPC 5-200的壓縮耗能分別增加至5.69倍、6.51倍和6.74倍，呈逐漸增大趨勢，其軸壓韌性比有所減小。

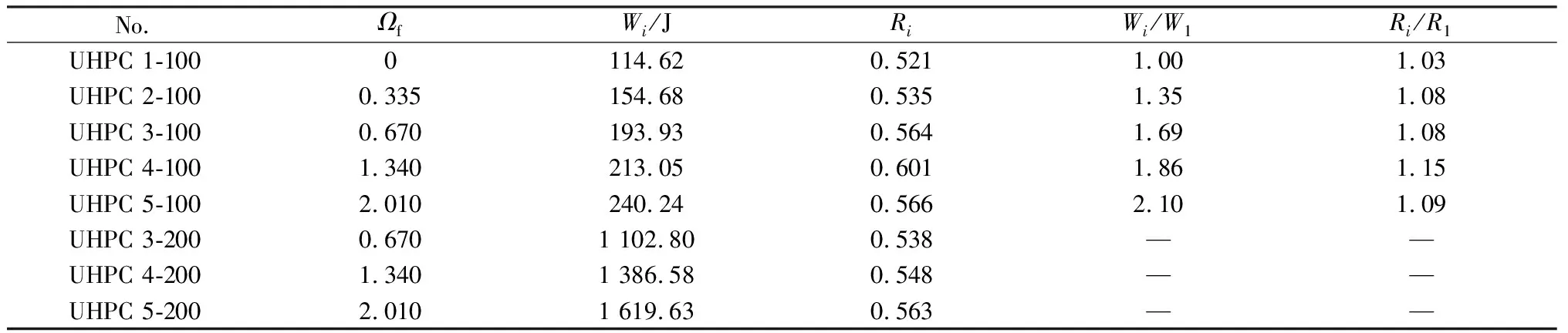
表5 Wi和Ri與Ωf關系Table 5 Relationship of Wi and Ri with Ωf

4 纖維約束對UHPC抗壓強度的影響

4.1 UHPC立方體抗壓強度

考慮纖維約束系數Ωf的影響，從試驗現象可知，端鉤型纖維主要約束試件受荷時的橫向變形，因此摻入纖維后能給UHPC提供一定環向約束[20]作用。對比胡翱翔等[16-17]和本文試驗結果，得出纖維約束系數與UHPC立方體抗壓強度的關系如圖10所示，由圖10可知，UHPC立方體抗壓強度隨纖維約束指數的增加呈曲線關系，將纖維約束UHPC立方體抗壓強度與素UHPC立方體抗壓強度相對值表示為：

(4)

式中：fcu,c為纖維約束UHPC的立方體抗壓強度；fcu,0為未摻纖維UHPC的立方體抗壓強度；a、b和c為待定系數。

基于試驗數據，經過回歸分析可得，對鋼纖維：a=1.1、b=0.064、c=0.041，R2=0.97，擬合得出的a值大于1，這可能是由于當纖維摻量為0%時，試件因局部損傷突然破壞，導致其試件的抗壓強度偏小。

圖11為UHPC試件抗壓強度與纖維約束系數的關系，對比胡翱翔等[16]得出的抗壓強度與纖維體積分數Vf之間的線性關系模型可知，本文基于纖維約束系數，提出的曲線關系模型可更好地預測端鉤型和直線形鋼纖維UHPC抗壓強度。

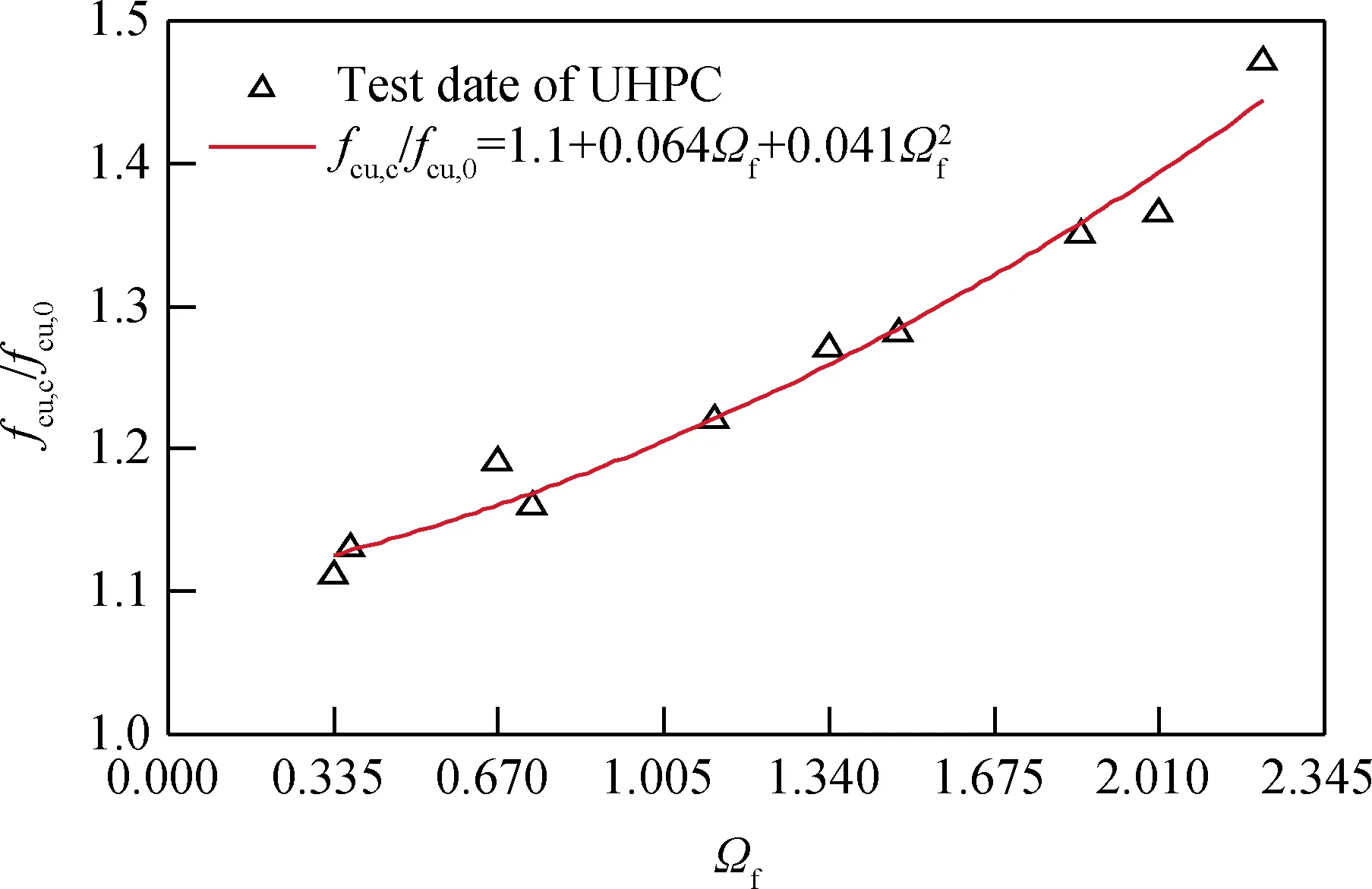
圖10 fcu,c/fcu,0與Ωf的關系Fig.10 Relationship between fcu,c/fcu,0 and Ωf of specimens

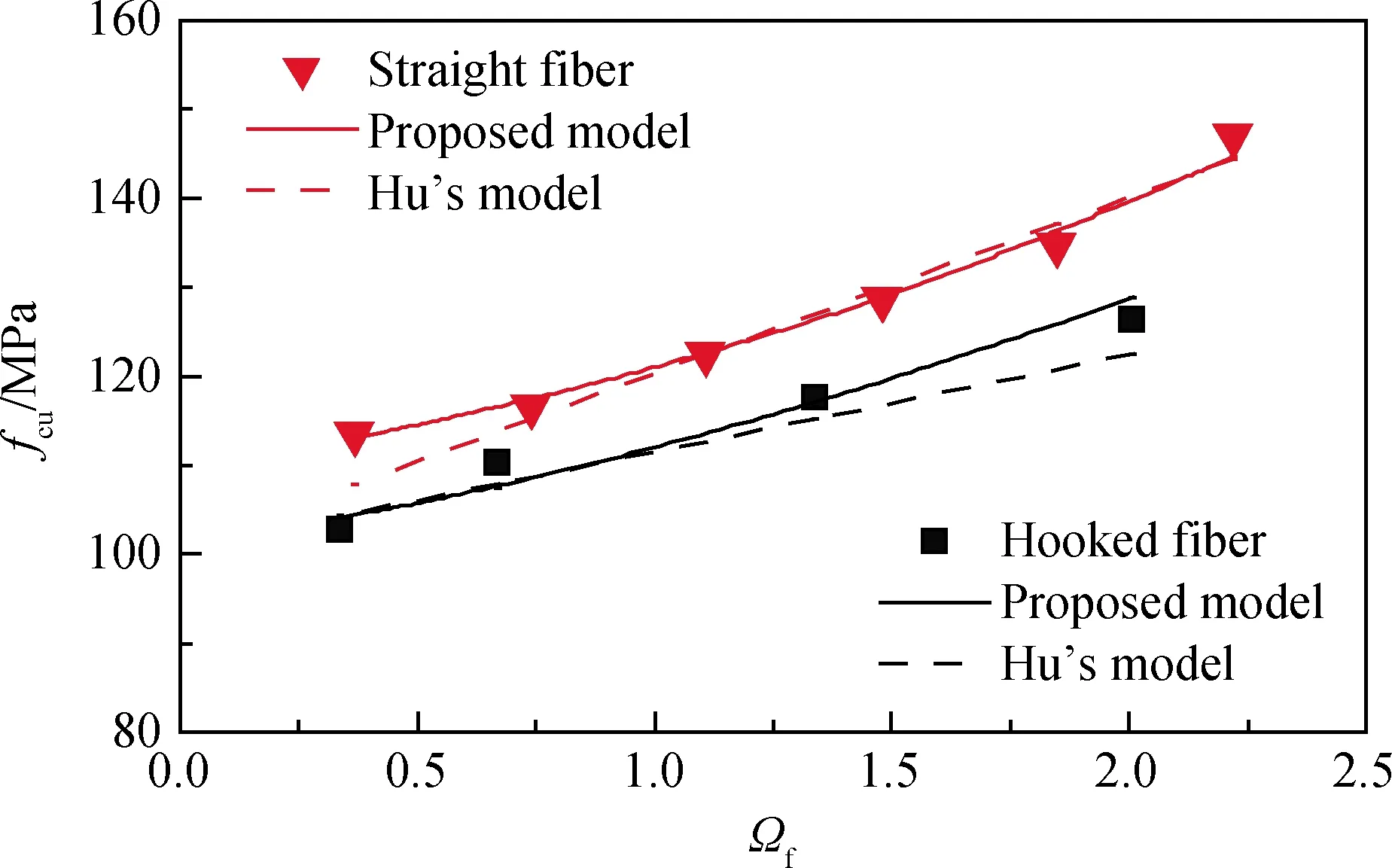
圖11 fcu,c與Ωf的關系Fig.11 Relationship between fcu,cand Ωf of specimens

4.2 UHPC峰值位移

圖12為δmax,c/δmax,0與Ωf的關系曲線，由圖12可知，約束UHPC試件的峰值荷載位移δmax,c/δmax,0值隨纖維約束系數Ωf的增大而增加，二者散點圖基本呈下凸曲線關系增長，故也可采用指數函數回歸擬合。

(5)

式中：δmax,c為纖維約束UHPC的峰值荷載相對應的壓縮位移；δmax,0為未摻纖維UHPC試件的峰值荷載相對應的壓縮位移；m、n、d為回歸分析待定系數。

經過回歸分析可知，對端鉤型鋼纖維：m1=0.001 8、n1=2.5、d1=1.147，R2=0.994，試驗得出的d值大于1，此現象纖維約束系數對UHPC抗壓強度的影響類似。

4.3 UHPC初始損傷強度

由圖13可知，約束UHPC試件的初始損傷強度fD0隨纖維約束系數Ωf的增大而增加，二者散點圖基本呈線性關系增長，故可采用直線進行回歸擬合。

fD0=AΩf+B

(6)

式中：fD0為纖維約束UHPC的初始損傷強度；A、B為回歸分析待定系數。

經過回歸分析可知，對端鉤型鋼纖維：A=11.38、B=36.36，R2=0.97。

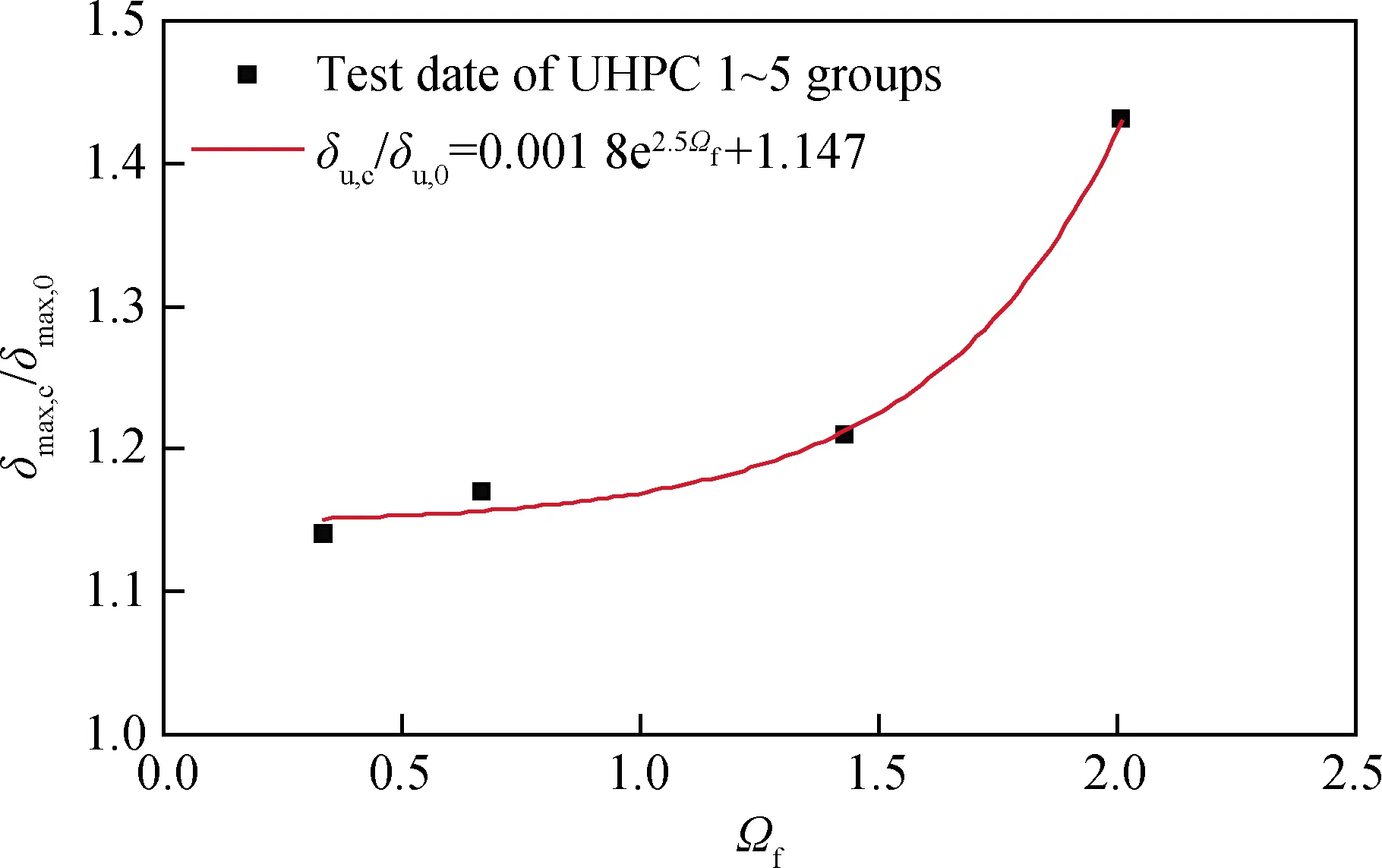
圖12 δmax,c/δmax,0與Ωf的關系Fig.12 Relationship of δmax,c/δmax,0 and Ωf of specimens

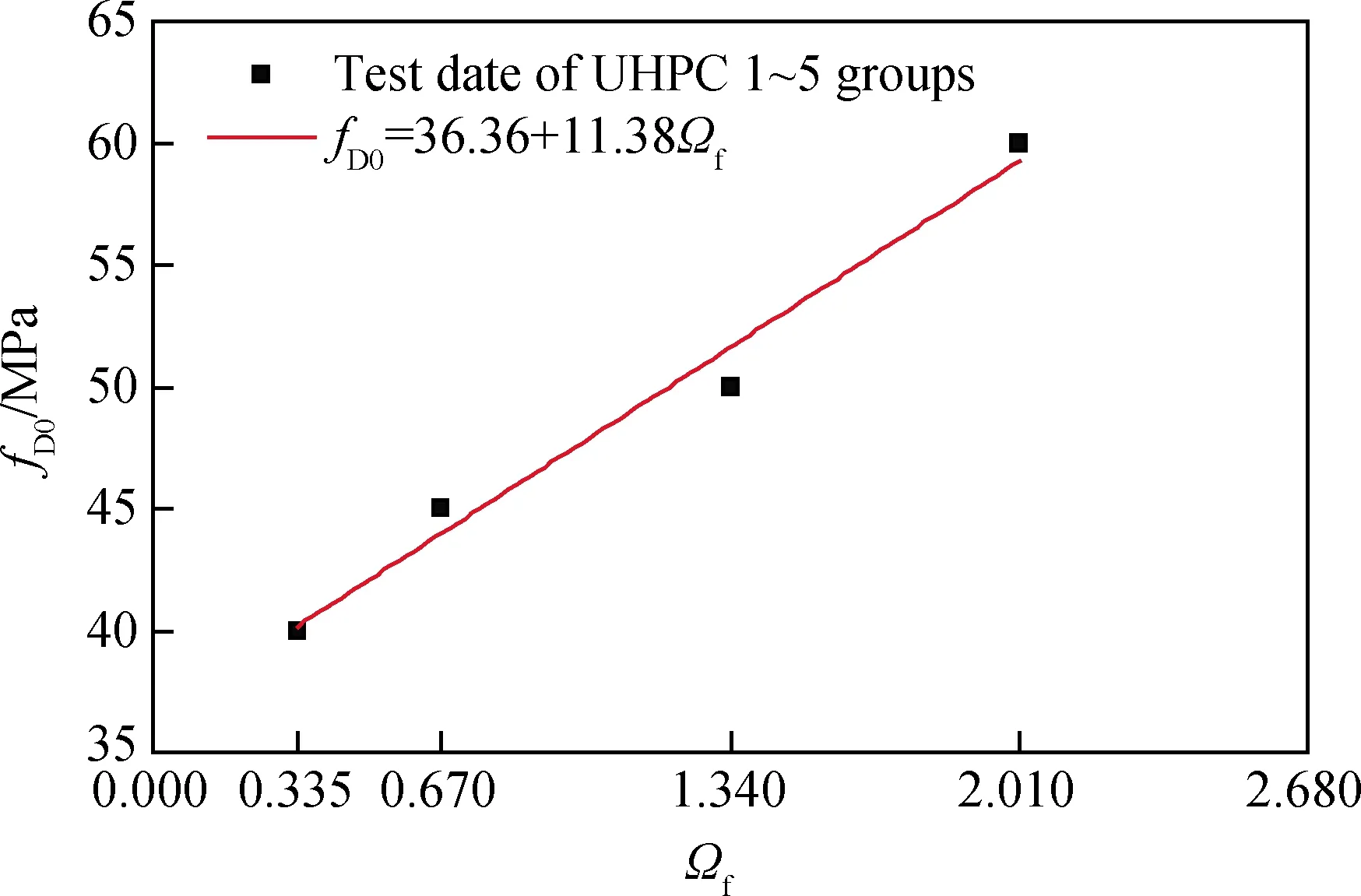
圖13 fD0與Ωf的關系Fig.13 Relationship of fD0 and Ωf of specimens

5 結 論

(1)與未摻纖維UHPC立方體試件相比，摻入端鉤型鋼纖維使試件在受荷達到極限荷載的40%左右時，開始產生纖維在UHPC基體中的拔出聲。隨著纖維約束指數的增加，UHPC試件的初始損傷對應的強度基本呈線性的增長。

(2)對未摻纖維UHPC試件，受荷破壞前無征兆，破壞后狀態更嚴重。而摻入端鉤型鋼纖維的UHPC試件最終破壞呈多條豎向裂縫，且最終破壞時試件仍能保持完整形態，呈現“裂而不碎”的狀態。

(3)隨著端鉤型鋼纖維體積摻量的增加，立方體試件抗壓強度增加，纖維摻量為3%時，增加37%，其抗壓強度相對應的試件變形也增大，纖維摻量為3%時，增加34%。與未摻纖維UHPC試件相比，纖維約束指數為0.335、0.670、1.340、2.010時，試件的壓縮耗能逐漸增大，纖維摻量為3%時，增加了110%。

(4)隨著纖維摻量的增大，尺寸效應對UHPC的影響逐漸減小。并考慮纖維約束指數Ωf，基于試驗結果和相關文獻，建立了UHPC立方體抗壓強度的預測模型，與試驗結果吻合較好。