基于變論域模糊PI的永磁同步電機無傳感控制

李瑞棋, 楊 波, 賀建湘, 陳 立

(1.哈電風能有限公司,湖南 湘潭 411101;2.海上風力發電技術與檢測國家重點實驗室,湖南 湘潭 411102；3.昆明理工大學 信息工程與自動化學院，云南 昆明 650504)

0 引 言

對永磁同步電機(PMSM)進行矢量控制必須得到電機的轉子位置以及轉速信息，而機械式的傳感器會帶來一定問題[1]，無傳感控制技術就此產生。根據額定轉速對無傳感控制法進行劃分，分為適用于低速以及中高速2大類。低速指的是在額定轉速10%處；中高速是指按照額定轉速的50%及以上。其中,中高速PMSM無傳感控制方法研究較為成熟，主要有模型參考自適應[2]、觀測器法等[3]。但是無法應用于低速控制，主要的原因是中高速無傳感控制法利用的是電機反電動勢進行估算，但是在低速階段較難檢測。低速階段主要利用高頻注入法進行PMSM無傳感控制，主要為脈振注入法、旋轉注入法等，但是這些方法不僅需要通過濾波器過濾出基波信號，還要過濾得到含有轉子位置信息的信號。而借助濾波器，不可避免使系統中信號滯后[4]，本文的研究方向放在低速無傳感控制上。

借助濾波器使系統存在滯后，這是造成轉子位置估算誤差的主要原因。大部分學者主要通過2個方向減少轉子位置估算誤差：第1類估算算法優化法，基本思路是通過不同電機本體參數形成預測模型，對估算算法進行優化。這類方法一般通過不同電機的參數進行優化，但是無法適用于不同電機；第2類通過對電機控制方法優化，高頻注入法主要依托于PMSM閉環矢量控制。其中包含2個閉環，即1個轉速環、1個電流環，通過PI控制器進行聯接。PI控制器控制簡單易于理解，但是普通的PI控制器無法減少高頻注入法產生的滯后，影響電機調速過程。文獻[5]提出借助滯環控制器代替電流環的PI控制器。雖然對系統的滯后進行一定的補償，但是影響了磁鏈的形狀，帶來電機振動等不必要的影響。文獻[6]通過電流預測控制代替電流環的PI控制器，優化了系統的延時，但是預測控制對于電機參數魯棒性較低，無法適用于不同電機。

本文通過變論域模糊的理論與方法，優化電機脈振注入法中的PI控制器參數，達到優化系統延時的問題。變論域模糊PI法通過利用伸縮因子來調整模糊論域進而調整PI的參數，從而改善系統的滯后，最終提高轉子位置的估算精度。本文在MATLAB/Simulink中搭建PMSM無傳感控制模型，然后用變論域模糊PI的方法來代替轉速環上的PI控制器，達到減少滯后的效果，最后通過仿真證明了該方法具有可行性。

1 傳統脈振注入法無傳感控制

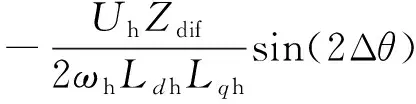
(1)

式中:Zdif=(Ldh-Lqh)/2;Ldh、Lqh分別為注入高配信號后旋轉坐標軸下的dq軸電感；Uh為高頻注入幅值；ωh為注入高頻信號的角頻率；Δθ為實際坐標軸與估算坐標軸位置差值。

整體程序框圖如圖1所示。

圖1 PMSM控制框圖

脈振估算系統框圖如圖2所示，此時得到了誤差信號。主要有2種方法得到轉子位置信息：第1種是龍伯格觀測器，這種觀測器精度高，但是需要額外轉矩傳感器；第2種是通過PI控制器控制估算誤差為0得到轉子位置信號。如圖1所示。

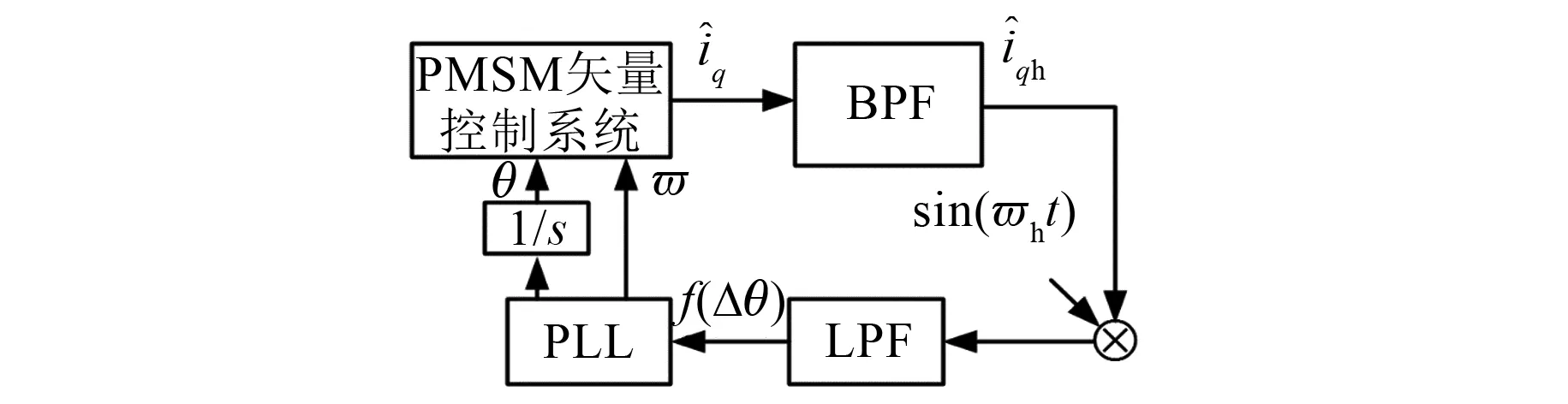
圖2 脈振估算系統

圖1、圖2中，有3個地方使用濾波器。電流環中使用了LPF，用來過濾注入的高頻信號，以及高頻信號疊加到變頻器上的多余高頻信號；帶通濾波器過濾出含有轉子位置信號的1 kHz頻率。

現在對帶通濾波器進行詳細分析，其需要過濾掉高頻信號、基波信號以及變頻器信號，得到1 kHz頻率。但是帶通濾波器過濾信號需要下一時刻的輸入，這通常導致輸出延時，由此得到轉速信息以及轉子位置信息也會存在延時[8-9]。脈振注入法中估算得到的轉速信息本身存在一定滯后，根據滯后得到q軸電流給定，通常導致電機控制給定信號滯后，對電機控制會造成一定的影響。

普通的PI控制器結構，無法對持續增長的滯后做一定優化，最終使得轉子位置的誤差較大[10]。

為了驗證這一分析，本文使用MATLAB/Simulink對傳統的高頻脈振注入法進行仿真，電機參數如表1所示。

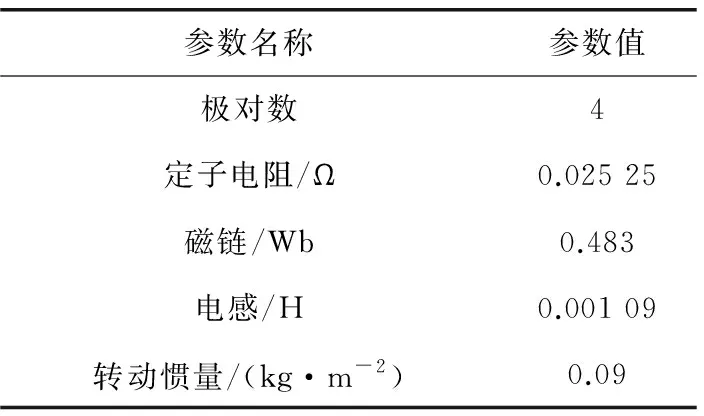
表1 電機參數

仿真結果如圖3所示。通過轉速信號分析電機是否能夠正常運轉；利用轉子位置分析電機運行狀態是否穩定。

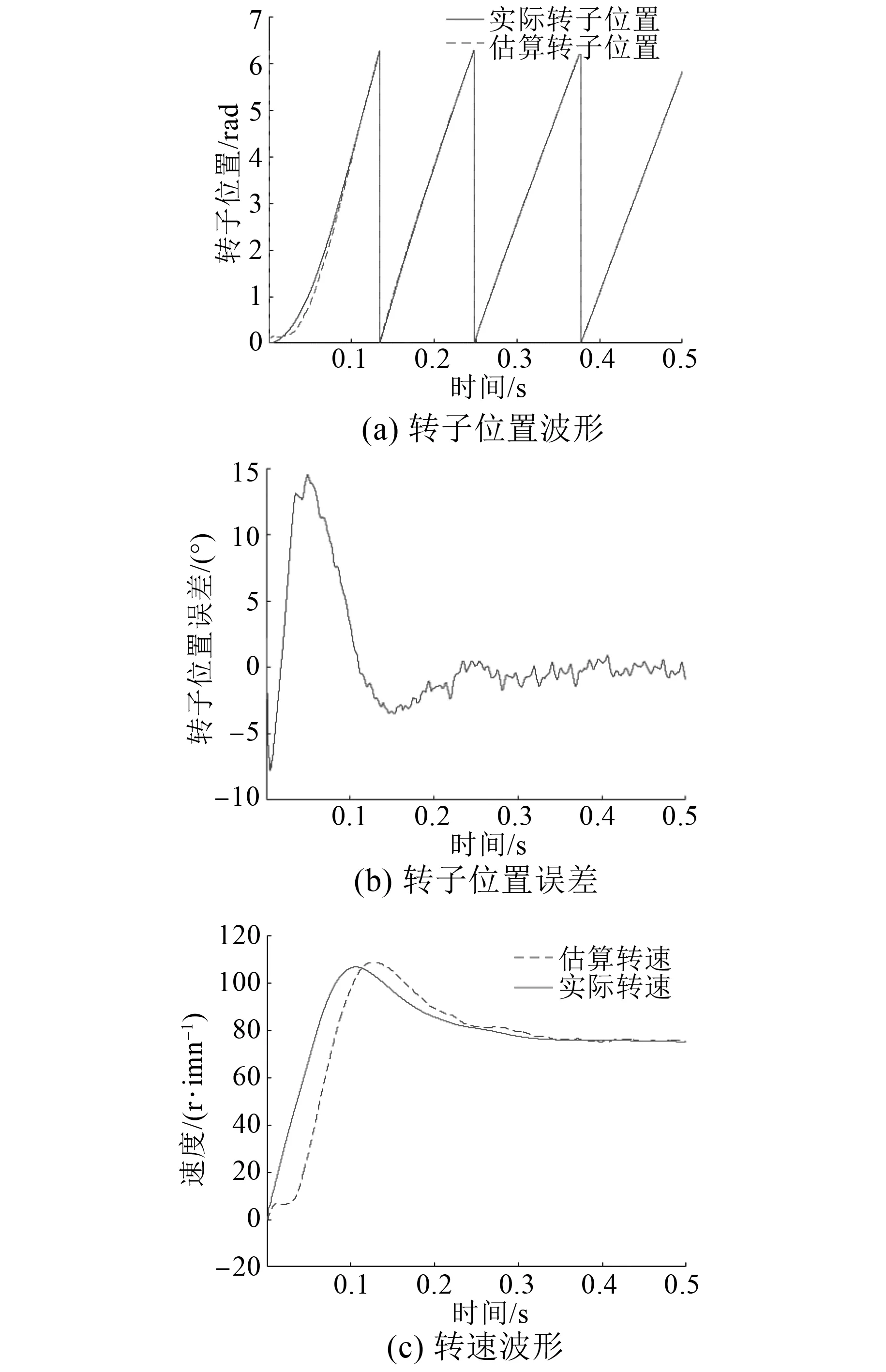
圖3 傳統方法仿真結果

從圖3(a)、圖3(c)可以看出傳統脈振注入法能夠滿足基本控制需求，但是最大誤差相對于穩定誤差相差較大，可以考慮對最大誤差優化，達到減少平均誤差的效果。從圖3(b)可以具體看出起動階段最大誤差為14.49°，相對于穩態過程誤差極大，通過解決最大誤差就能夠減少整體平均誤差。

為了對帶通濾波器的能力進行一定說明，本文在MATLAB中設計了仿真試驗。

給定信號為最大值10的1 kHz基頻信號、2π*1 kHz高頻信號和50 Hz低頻信號疊加，信號幅值為10～20。由于高頻注入給定信號為2π*1 kHz，則疊加高頻信號同樣為2π*1 kHz。帶通濾波器為了得到轉子位置信息，脈振注入法中用來過濾出1 kHz信號，所以試驗設置相同，基頻信號設置為1 kHz。而PMSM電源頻率為50 Hz，同樣設置低頻信號為50 Hz。為了與本文控制系統接近，本文所有帶通濾波器參數如表2所示。

表2 帶通濾波器參數

仿真結果如圖4、圖5所示。

圖4展示的是過濾信號輸出結果對比圖，可以看出經過一段時間以后，能夠過濾出實際信號，說明帶通濾波器在本文中能夠使用。但是從0 s以及0.1 s 2個時刻的對比可以看出，信號階躍時帶通濾波器很難追蹤實際信號，與上一時刻的信號存在一定嚙合，無法快速接近實際信號。圖5為圖4在0.08 s左右的對比圖，通過圖5可以看出，即使穩定之后，信號也存在一定的延時以及幅值衰減。

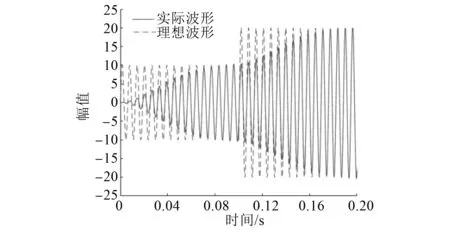
圖4 濾波對比

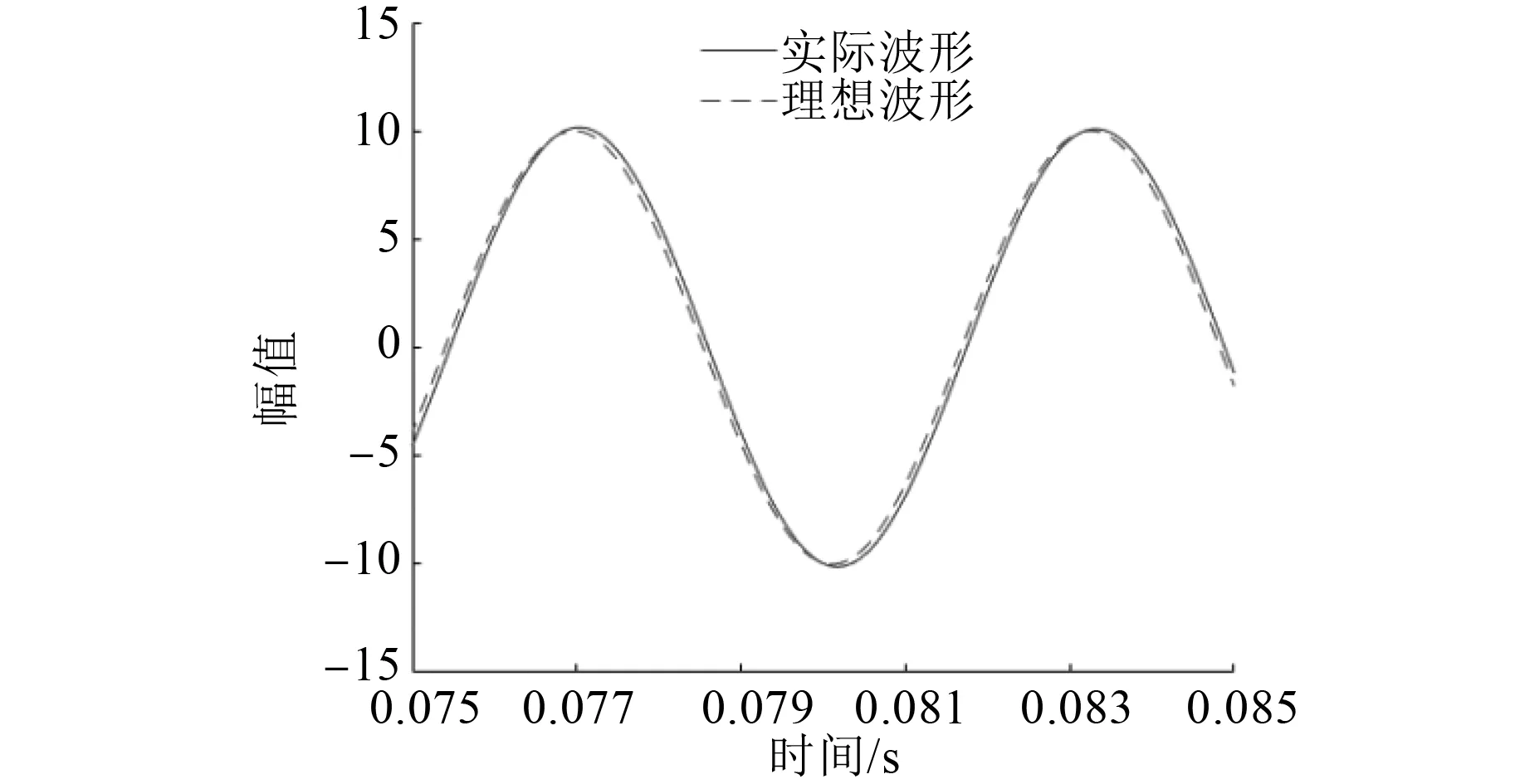
圖5 信號穩定之后波形對比

2 變論域模糊轉速環設計

按照上文分析在采用高頻脈振注入法的無傳感控制中，由于濾波延時的存在，會導致的估算出的轉速以及轉子位置滯后于實際值，并且不同時期信號延時以及幅值衰減有一定的區別。而普通的PI調節器本身不具備補償反饋通道信號滯后的能力，不足以根據不同的信號延時、幅值衰減進行調節。因此本文考慮通過變論域模糊PI控制器代替速度環中的PI對系統存在的滯后進行一定的優化，達到減少轉子位置估算誤差的結果。

2.1 模糊自適應PID控制算法

傳統PID控制器雖然原理簡單，但是無法應用于復雜場合，對于階躍信號、滯后情況無法很好地優化。而模糊控制PID通過輸入模糊、自適應模糊推理以及最后的去模糊化達到模糊控制的效果[11]。

本文設計的模糊控制器的輸入是：給定的轉速值和含有滯后信號的轉速估算值相減的誤差e和誤差的變化率ec，輸出是ΔKI、ΔKP和ΔKD。

由于模糊控制只能處理模糊值，將確定值的輸入模糊化，將給定轉速以及估算轉速的誤差、誤差變化率量化因子Ke與Kec一一對應。可以設置模糊論域寬度為6，其中包括e、ec和ΔKP。設置大于0的模糊論域ΔKI和ΔKD，為[0，6]。而模糊論域主要采用7種模糊語言[12]。最后的輸出結果如下：

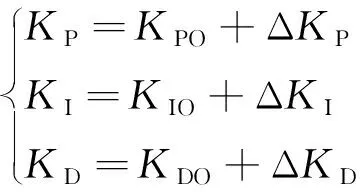
(2)

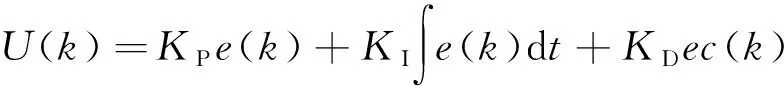
(3)

式中:U(k)為模糊控制器最后的輸出；KPO、KIO、KDO為PID參數給定的初始值；KP、KI、KD為PID控制器最終輸出。

ΔKI、ΔKP和ΔKD的模糊規則推理表參考文獻[12]。

2.2 變論域模糊控制器

變論域與模糊結合的基本思路是：結合變論域的伸縮因子與模糊的論域，表達式為

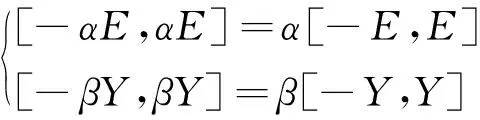
(4)

式中:[-E,E]、[-Y,Y]分別為輸入、輸出模糊初始論域；α、β分別為輸入輸出的伸縮因子。

由于伸縮因子的存在，可以借助伸縮因子動態調節初始論域，通過對比估算轉速與給定轉速的誤差，如果誤差較大，這時論域會被擴大，通過模糊規則降低結果敏感性，減少動態誤差[13]。

論域的伸縮變化圖如圖6所示。

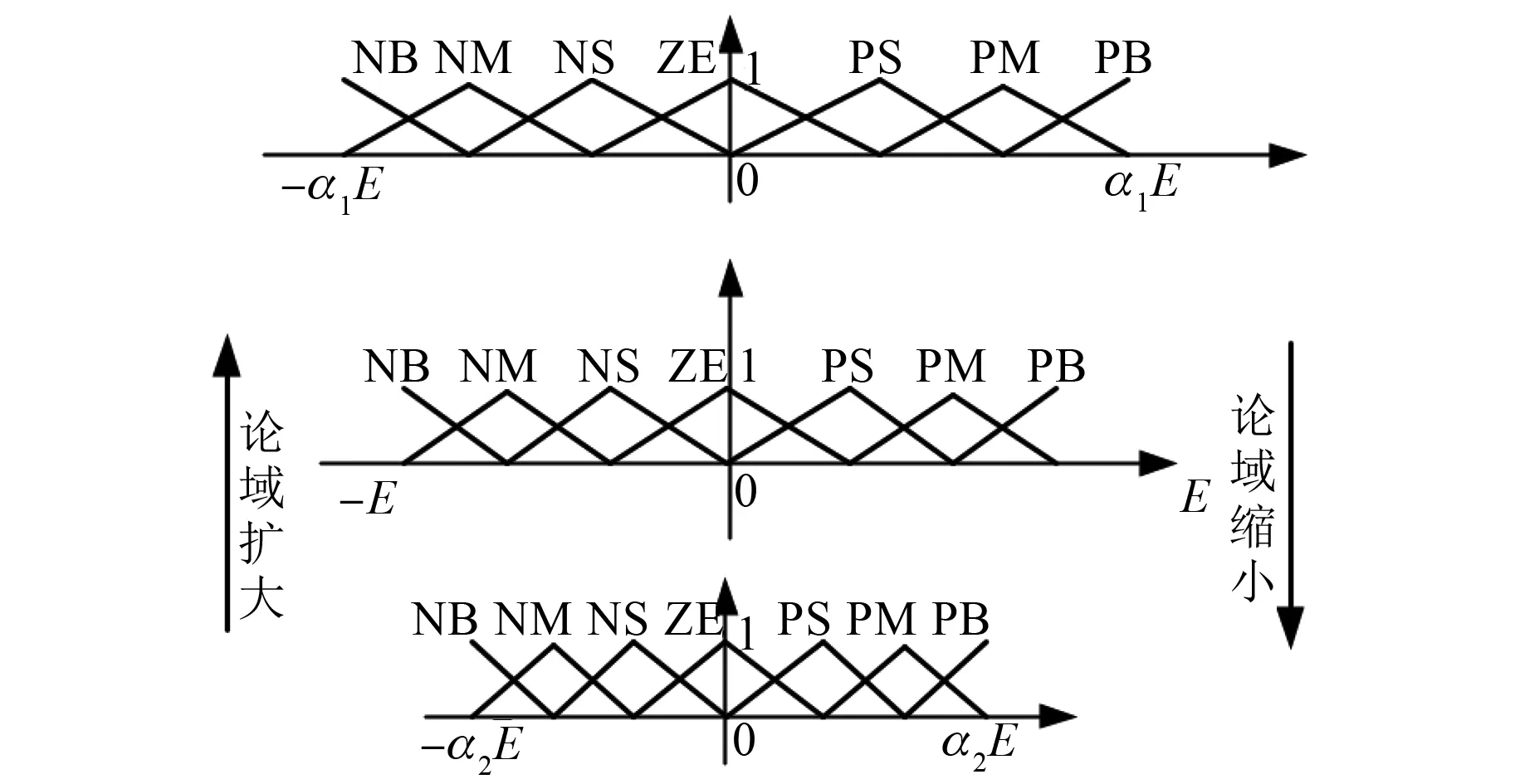
圖6 論域的伸縮變化情況

對于變論域模糊控制效果，十分重要的因素就是較為準確給定伸縮因子，可以通過式(5)、式(6)進行推導：

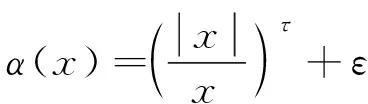
(5)

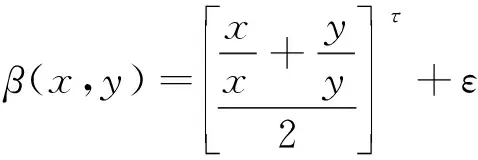
(6)

式中:τ>0，ε為極小正數；α(x)為輸入論域的伸縮因子；β(x,y)為輸出論域的伸縮因子。

通過不同PID參數對轉速環的控制，減少轉子位置估算誤差，最終實現對電機無傳感控制，本文無需D參數，設置為零即可。

本文無傳感控制整體框圖如圖7所示。

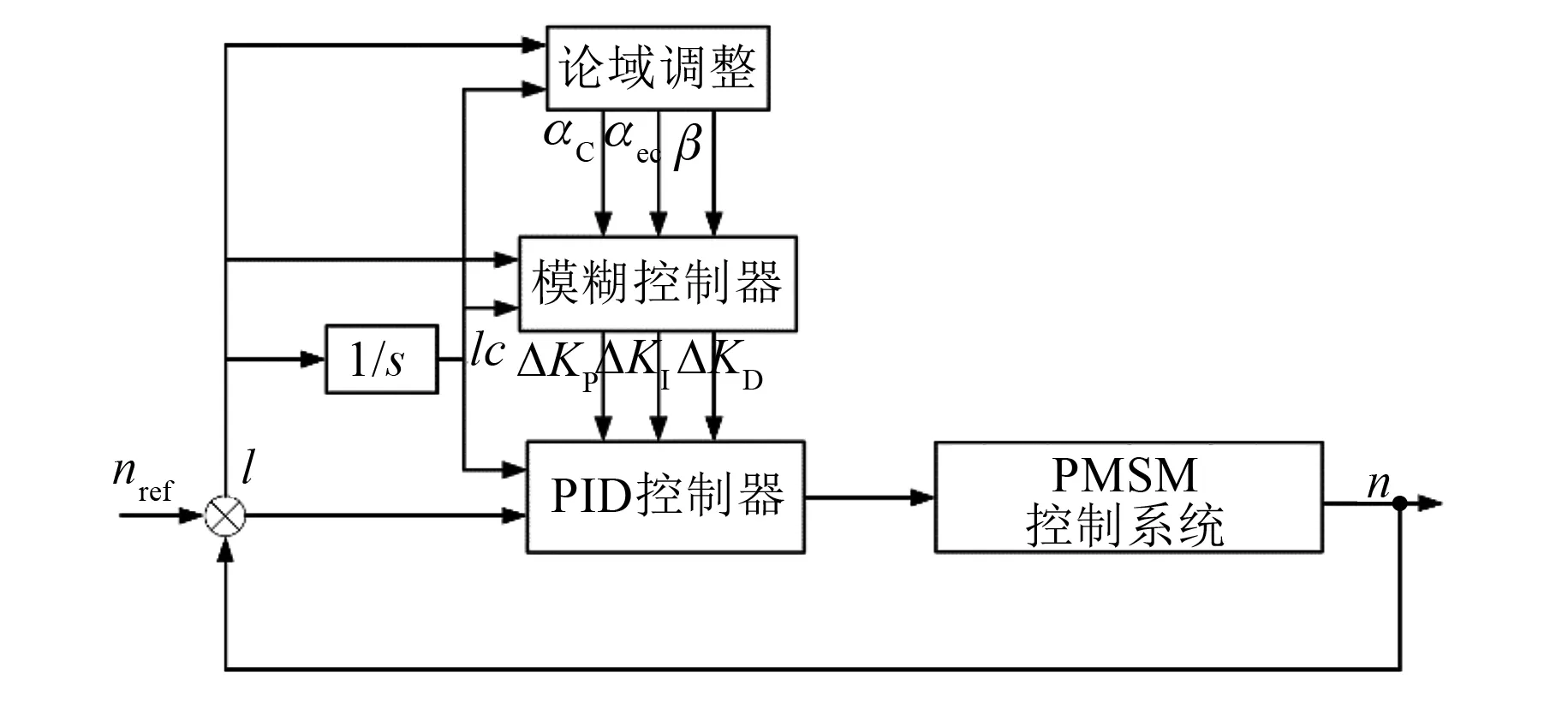
圖7 變論域PID無傳感控制框圖

3 仿真分析

為了驗證本文方法的有效性，與上文所做的試驗環境相同。在額定轉速750 r/min下進行試驗。試驗結果如圖8所示。

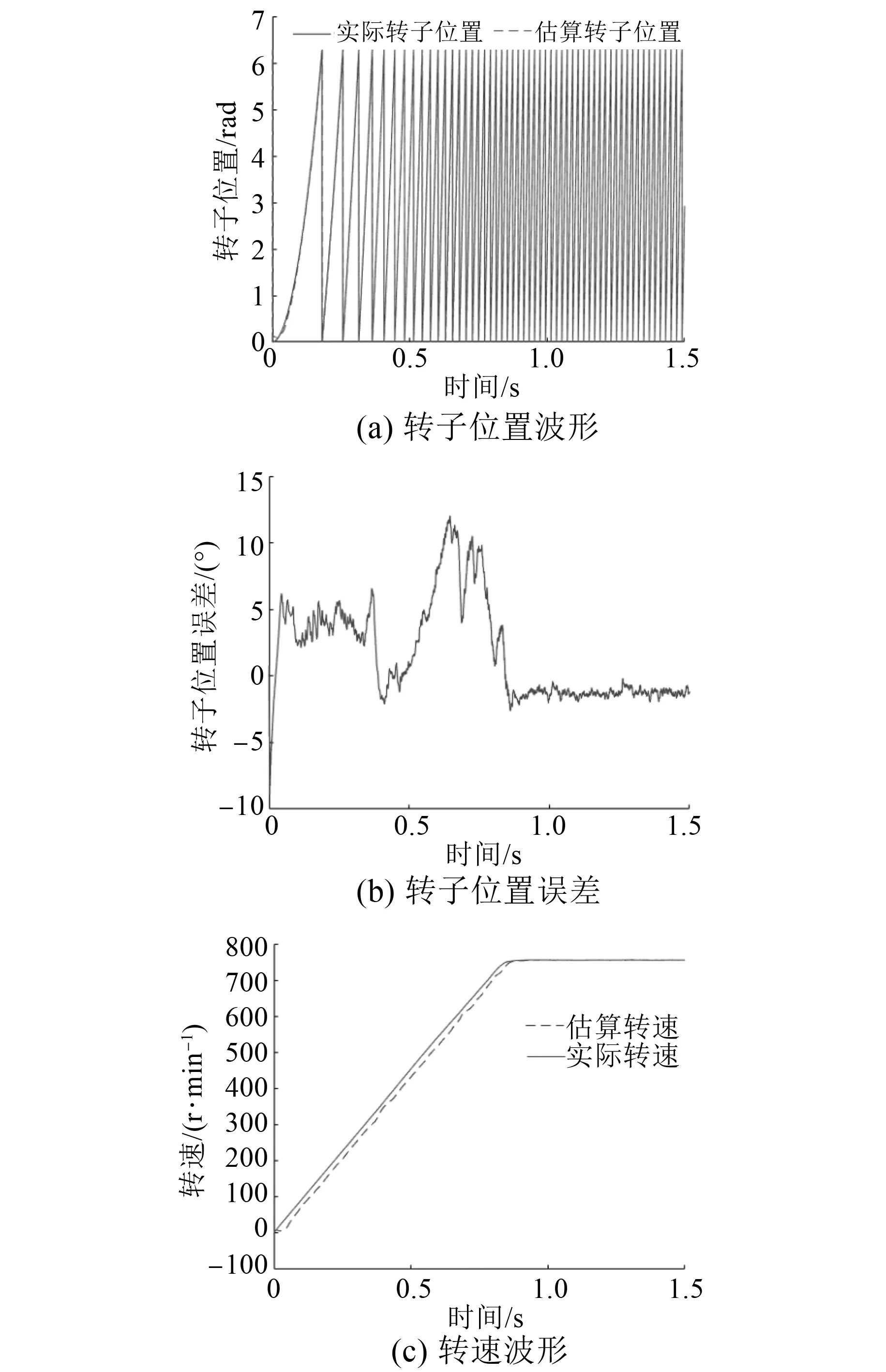
圖8 額定轉速下試驗結果

在額定轉速下試驗，主要目的是展示本文方法的適用性。從圖8(c)中可以看出，本文所提方法調速性能較好，基本無超調量，電機起動穩定；從圖8(a)、圖8(b)可以得出本文方法，對轉子位置估算較準確，可以適用于位置控制系統。說明本文使用的變論域模糊PI控制器能夠提高電機調速性能。

為了與上文所做的傳統脈振注入法進行對比，同樣在75 r/min給定轉速下進行電機無傳感控制試驗。其中帶通濾波器的參數設計與上文相同為，導通頻率960 Hz，關斷頻率1 040 Hz，階數位2。試驗結果如圖9所示，具體轉子位置誤差如表3所示。

圖9 75 r/min轉速下試驗結果

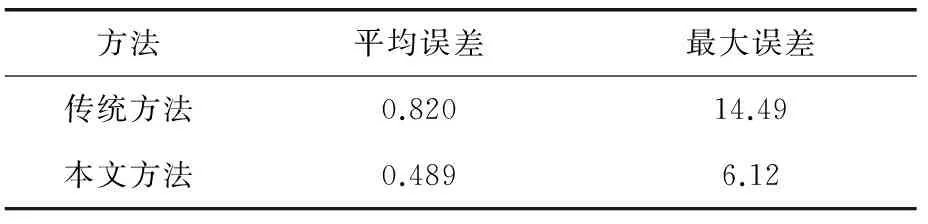
表3 75 r/min誤差對比(°)

圖9展示的是本文方法下的仿真試驗結果，給定轉速為75 r/min，為與傳統方法對比，同樣運轉電機0.5 s。由圖9(a)對比圖3(a)可以看出，2種方法下估算轉子位置均能夠很好地擬合實際轉子位置，但是本文方法相對傳統方法在起動階段能夠更好擬合轉子位置；從圖9(c)對比圖3(c)可以看出通過變論域模糊PI對轉速環進行控制，相對傳統方法能夠減少轉速的超調量，轉速穩定之后通過模糊控制能夠擬合實際轉速；結合表1以及圖9(b)得出本文方法能夠在起動過程減少轉子位置估算最大誤差到6.12°，平均誤差減少到0.489°。

結果表明本文方法能夠有效減少轉子位置估算誤差，魯棒性較好。

4 結 語

本文分析了PMSM脈振注入法延時存在的原因。為了減少常規脈振注入法系統延時導致轉子位置估算精度較差的問題。提出了一種基于變論域模糊PI的脈振注入法。分別在額定轉速下，以及10%額定轉速下進行試驗。試驗結果表明本文所提方法減少了轉子位置估算誤差，平均誤差從0.82°減少到0.489°，最大誤差從14.49°減小到6.12°。滿足低速下無傳感控制，并且同樣可適用于高速階段。