煤礦井下巷道全斷面風速場分布規律

王 航

(陜煤集團神木張家峁礦業有限公司，陜西 神木 719316)

0 引言

礦井通風安全是煤礦安全的核心和基礎，是煤礦生產的生命保障系統，但煤礦一般都存在通風監測準確性低、關鍵用風點風量管控效率低等問題。為了保證礦井通風安全的可靠性和有效性，提高礦井通風自動化、信息化和智能化的水平，適應新時代智能化礦山建設發展的需求，實現礦井通風的實時監測及風量最優調控方案決策。不同巷道斷面的風速分布規律受巷道斷面形狀、巷道支護類型、巷道內布置設備影響，巷道風流脈動特性和巷道斷面風速非均勻分布規律導致定點安設的風速傳感器測試巷道的平均風速方法難以實現準確測定或適用性相對有限，無法解決任一巷道平均風速測試問題，可推廣性相對不足，如何通過風速傳感器等測風設備，構建具有大面積推廣的巷道平均風速測試方法是目前需要解決的難題，研究并掌握矩形、拱形等不同巷道斷面內風速分布規律，掌握高風速區域、中風速區域和低風速區域就成了所有基礎數據采集的關鍵所在。

1 巷道全斷面風速場數值模擬幾何模型

陜煤集團神木張家峁礦業公司井下巷道測風站包括矩形和半圓拱2類巷道斷面。為了掌握矩形巷道與半圓拱巷道斷面內風速分布規律，利用GMBIT建模軟件構建與實際巷道尺寸按比例的矩形巷道與半圓拱巷道風流場數值計算的幾何模型，如圖1所示。為了重點考慮巷道尺寸對巷道斷面風速場的影響規律，建立了多種尺寸規格的矩形巷道與半圓拱巷道風流場數值計算的幾何模型，具體尺寸參數見表1、表2。在建立幾何模型的基礎上，需要對幾何模型進行計算單元劃分，計算單元選擇正六面體，將完整的巷道幾何模型劃分為N個正六面體計算單元，如圖2所示。

圖1 巷道模型示意Fig.1 Schematic diagram of roadway model

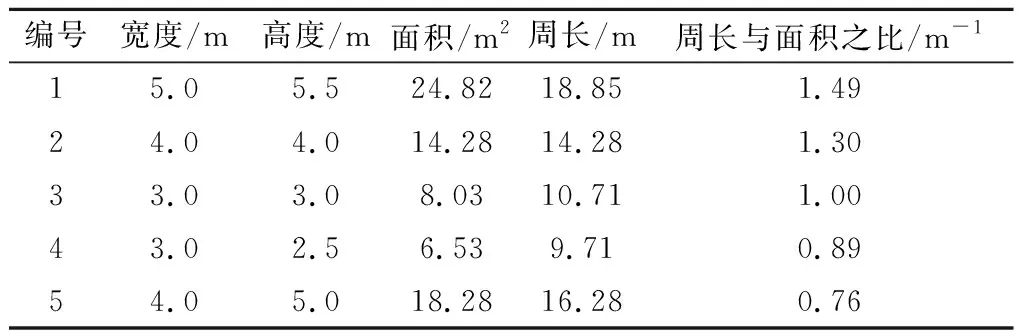
表1 半圓拱巷道模型

表2 矩形巷道模型

2 巷道全斷面風速場數值模型

2.1 巷道風速場CFD計算模型的建立

井下巷道內空氣流動過程滿足質量守恒、動量守恒、能量守恒，可用N-S方程組求解，巷道風流場解算N-S控制方程組見式(1)，考慮巷道內風流狀態為紊流，因此需要在上述廣義N-S方程組基礎上補充湍流模型方程組，由于巷道為受限空間且人員的存在使得巷道風流場邊界條件相對不確定[1]，導致某些特定區域風流截面會發生不可預期變化，利用REGk-ε模型，可較好地描述風流高應變率及流線彎曲程度大的流動，那么廣義N-S方程組與REGk-ε模型聯立且在此基礎上再加上邊界條件，則可確定完整的可求得近似解的巷道風速場CFD計算模型。

圖2 網格劃分局部放大Fig.2 Local of meshing

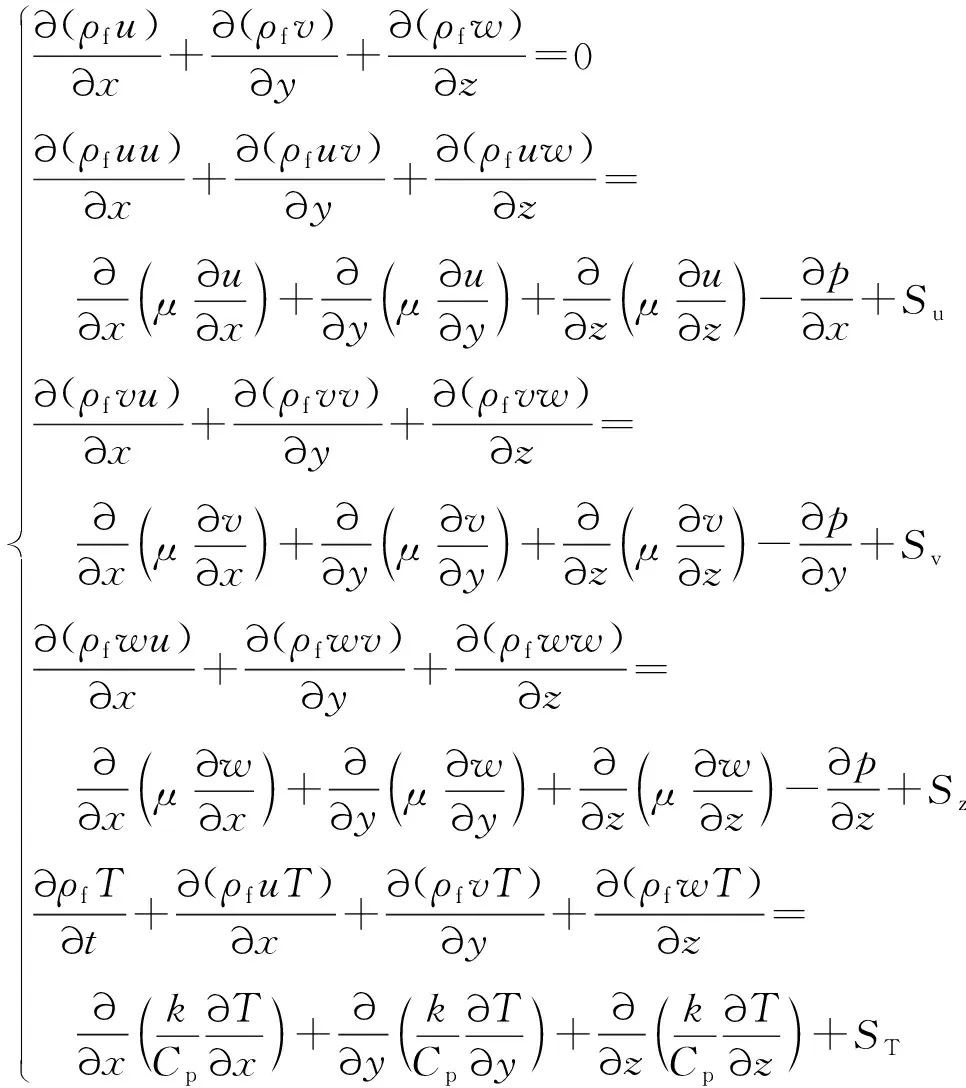
(1)

式中，ρf為風流密度，kg·m-3；v為計算區域內某一位置y方向風速，m·s-1；u為計算區域內某一位置x方向風速，m·s-1；μ為空氣動力黏度，取值為17.9×10-6Pa·s；w為計算區域內某一位置z方向風速，m·s-1；Su為x方向的動量源項，kg·m-2·s-1；P為氣體壓力，Pa；Sw為z方向的動量源項，kg·m-2·s-1；k為空氣傳熱系數，取值為0.023 W·m-1·K-1；Sv為y方向的動量源項，kg·m-2·s-1；CP為空氣比熱容，取值為717 J·kg-1·K-1；T為氣體溫度，K；ST為黏性耗散項，J·m-3·s-1。

2.2 風硐風流場數值計算模型的建立

風硐內風流亦為紊流狀態，那么風硐內風流場須在N-S方程組上加載湍流模型方程組，一般風硐結構復雜，幾乎均為拱形斷面，使得風硐內流場邊界條件更加復雜，特別是風流斷面發生劇變的區域[2-7]，同時，REGk-ε模型也可很好地處理高應變率及流線彎曲程度大的流動，同樣適用于模擬風硐紊流風流問題，式(2)與式(3)為REGk-ε模型的控制方程。

(2)

(3)

式(1)、式(2)、式(3)聯立即為風硐風流場數值計算模型的方程組，加上表3所列的邊界條件，即構成了風硐風流場數值計算模型。

表3 計算模型邊界條件

3 巷道全斷面風速場數值模擬分析

3.1 巷道全斷面風速場模型的數據準確性論證

利用CFD數值模擬方法研究巷道全斷面風速場分布規律的前提條件是CFD數值模擬方法的巷道風流場數值模擬結果與實際巷道風流場實測結果一致[8-9]。目前，采用懸掛風速傳感器實測巷道斷面單點風速，通過對比巷道斷面同一位置風速傳感器實測值與數值模擬結果值，如果2個值之間相對誤差很小，則可認為巷道斷面風速場數值模擬結果與巷道斷面實際風速場一致，論證了巷道全斷面風速場模型的數據準確性。

3.2 風速傳感器所在位置實測值與模擬值對比

井下各地點的測風站巷道內的紊流風流，任意位置處點風速是脈動風速與主風速之合，因此風速傳感器數據具有明顯的波動性[10-12]。通過對現場實驗時間段內風速傳感器數據值求平均值，從而獲得風速傳感器測試值，人員與風速傳感器處于巷道同一斷面但不同位置條件下風速傳感器測試值。人員所在測風站位置處巷道斷面風速分布模擬結果，首先提取該巷道斷面內風速傳感器(巷道中垂線距巷道頂板1 m位置處)點風速數據，點風速模擬結果數據見表4。通過表4中的風速傳感器實際平均值與數值模擬值對比，可以得出數值模擬結果與實測結果相對誤差在2.5%以內，同時可知巷道內無人員的時候風速傳感器數據更加準確，說明了CFD數值模擬方法的風速場數值模擬結果能夠真實反映煤礦井下巷道內風速分布情況。

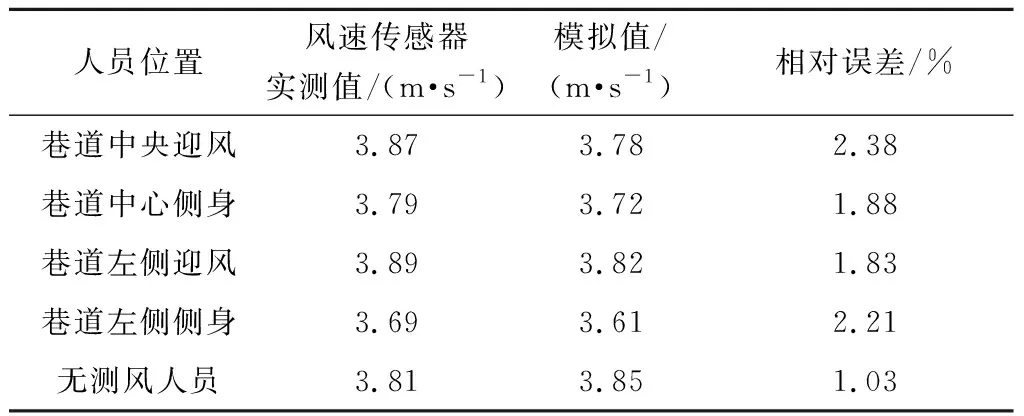
表4 風速傳感器所在位置實測值與模擬值對比

3.3 巷道全斷面風速場數值模擬結果分析

圖3為不同平均風速條件下序號1半圓拱巷道斷面對稱軸上風速分布，由圖3可得靠近巷道頂板、底板、巷道幫的巷道斷面位置風速明顯小于巷道斷面中部區域，巷道斷面風速變化具有連續性，寬度為5 m、高度為5.5 m的半圓拱巷道在巷道斷面寬度方向上風速非均勻區間長度達到2 m左右，風速非均勻區間長度隨巷道平均風速增大而顯示出明顯的增大趨勢。不同風速條件下巷道斷面內風速的不均勻分布程度為準確測得巷道風量增加了難度。在掌握巷道斷面風速場結構的基礎上，有針對性地布置風速傳感器進行測風，能夠準確測試巷道平均風速，進而計算得到巷道風量。

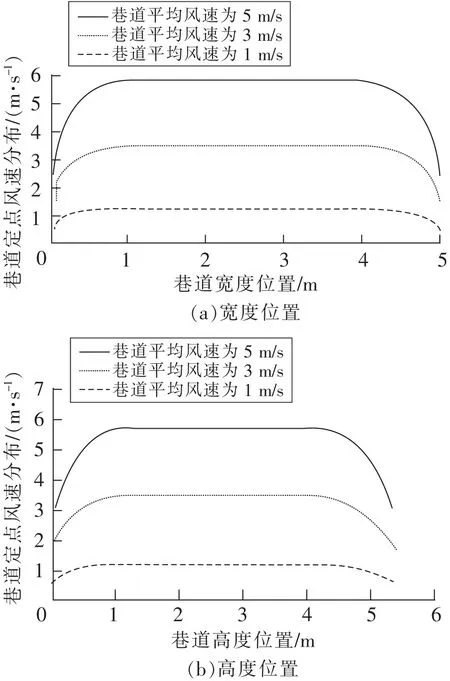
圖3 序號1半圓拱巷道斷面對稱軸上風速分布Fig.3 Wind speed distribution on symmetrical axis of semi-circular arch roadway section

4 結論

(1)采用CFD流體動力學數值模擬方法計算了矩形巷道、半圓拱巷道斷面風速場分布規律，結合風速傳感器監測數據驗證了數值模擬結果的可靠性，在此基礎上，模擬計算得到巷道斷面內平均風速區域，揭示了巷道風量大小對于巷道斷面平均風速分布區域影響可忽略，巷道尺寸大小是巷道斷面平均風速分布區域的主要影響因素。

(2)為了提高巷道斷面平均風速測定準確性，可在井下巷道全斷面進行平均風速9點測風法測定，此法可通過測試8個平均風速分布區域內位置風速值計算巷道平均風速，利用巷道中心區域風速監測點進行測試數據的進一步校驗，最終消除偏差較大數據。

(3)利用數值模擬方法對張家峁全礦井23個主要測風站巷道斷面風速場進行研究，可確定巷道斷面平均風速分布區域，對巷道斷面內9個風速監測點具體位置進行計算，取得了最優數據。為了實現巷道全斷面9點測風這一過程，礦井在實際作業中針對矩形巷道設計研發了龍門式全自動測風系統，針對拱形巷道設計研發了折疊式全自動測風系統，保證了風量測定的準確性。現階段，張家峁全礦井23個主要測風站均安裝了巷道全自動測風系統，通過對比同一時間段內人工測風數據和自動測風裝置測試數據，2種測風方法的相對誤差在5%以內，研究表明全自動測風系統的測風精度足以滿足礦井風量測試精度要求，實現了礦井主要大巷風量的自動測定。