基于熱約束的功率器件散熱器成本最小化方法

趙文博， 應展烽， 宋新陽， 許芮豪

(南京理工大學能源與動力工程學院， 南京 210094)

隨著光伏和風力發電技術的不斷發展，功率金屬-氧化物半導體場效應晶體管(metal-oxide-semiconductor field-effect transistor, MOSFET)和絕緣柵雙極型晶體管(insulated gate bipolar transistor, IGBT)等功率器件已經在離網逆變器和并網變流器等電力電子裝置中得到廣泛應用[1-3]。受到導通和開關損耗作用，功率器件在工作過程中會產生一定熱量。當散熱性能不佳時，器件便會面臨著嚴重的高溫失效風險，并極易引發電力電子裝置的熱故障停機。為了提升器件散熱能力和電力電子設備熱可靠性，功率器件上需要加裝散熱器。

當前市面上常用的散熱器一般為鋁制或銅制散熱器。在材料確定后，散熱面積和質量便成為散熱器的兩個重要參數。其中，散熱面積影響著散熱器的對流熱阻，而質量決定了散熱器熱容。對流熱阻和熱容又影響著功率器件的最高結溫及其熱時間常數。最高結溫直接決定了功率器件是否會發生過溫，而熱時間常數則表征了器件的溫升速率，影響著器件老化壽命。因此，散熱器質量和散熱面積均與功率器件的熱安全性緊密相關。從理論上看，散熱器質量和散熱面積的取值越大，器件的熱安全性則越強。但增大質量則會加大銅鋁金屬的投入，增加材料成本；而增大散熱面積會復雜化工藝流程，增加加工成本。因此，散熱器的質量和散熱面積不能任意增大，否則將影響散熱器的綜合成本，進而影響整個電力電子設備的成本。尤其對于大功率電力電子設備而言，由于散熱器結構復雜且質量較大，其成本將嚴重影響產品經濟效益。

目前已有大量關于散熱器設計或選型方面的研究。文獻[4-6]分別通過有限元、神經網絡以及熱網絡模型，對加裝了散熱器的功率器件進行熱可靠性分析，所得結果有助于驗證散熱器選配的有效性；文獻[7-8]對管片式散熱器進行數值模擬，明確了翅片類型、參數及位置對散熱器的散熱性能影響；文獻[9-10]利用有限元方法建立了熱-流體耦合仿真模型，分析了極端環境下的功率器件及散熱器熱特性，并通過增材制造技術對散熱器結構進行了設計。

上述研究表明，熱分析手段可有效驗證或修正散熱器參數，使其滿足散熱設計要求。對不同散熱器進行熱分析和參數調整后，便可實現散熱器的成本控制。然而目前缺乏針對散熱器選型和設計的優化方法研究，這會在工程上導致兩個問題。其一，散熱器參數調整嚴重依賴人為經驗，缺乏調整依據，存在盲目性。往往需要人為多次的反復迭代，才可能找到符合安全性和成本要求的散熱器參數；其二，無法保證散熱器參數的最優性。即便找到了滿足器件熱安全性要求的散熱器參數，也無法保證該組參數能夠使散熱器成本最小化。

為了在不影響功率器件熱安全性的前提下，充分實現散熱器的成本控制，現提出一種散熱器成本的最小化方法。該方法在功率器件熱網絡模型的基礎上，以器件最大結溫和熱時間常數為熱安全約束量，通過非線性優化算法，找尋最佳的散熱器質量和散熱面積參數，使散熱器成本最小化。以期為散熱器的合理設計或選型提供重要依據。

1 功率器件熱網絡模型

1.1 熱網絡模型結構

熱網絡模型是一種描述功率器件及其散熱器熱動態特性的有效方法。典型的熱網絡模型是一種結-環境模型，由結-殼熱網絡和殼-環境熱網絡兩部分組成。以一個分立型功率MOSFET為例，圖1給出了結-環境熱網絡模型的基本結構[11]。

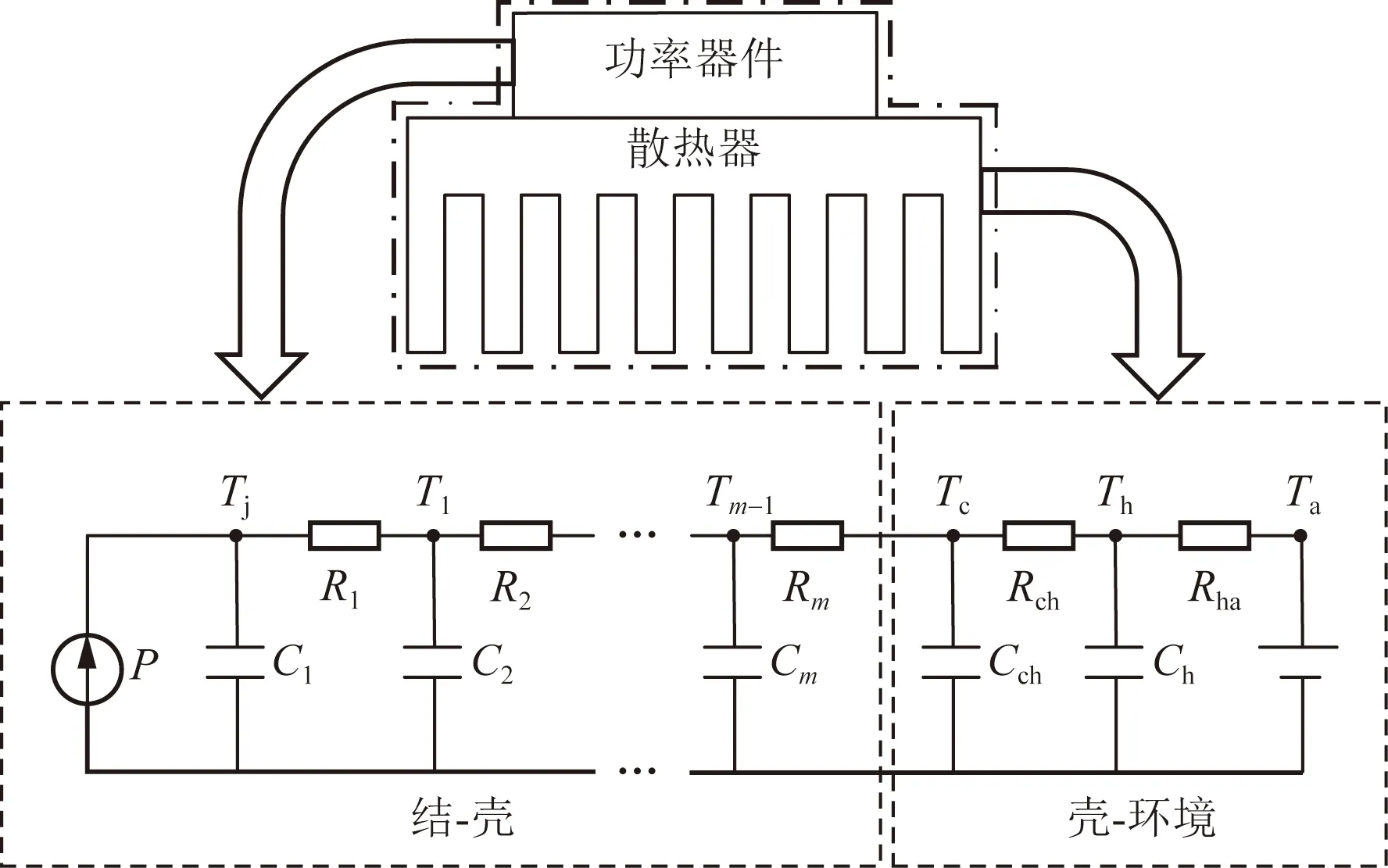
P為器件損耗；Tj和Tc分別為器件結溫和殼溫；Th和Ta分別為散熱器溫度和環境溫度；T1～Tm-1、C1～Cm和R1～Rm分別為結-殼中各節點的溫度、熱容和熱阻；m為網絡節點數；Cch為殼與散熱器之間導熱材料熱容；Ch為散熱器熱容；Rch為殼與散熱器之間導熱材料的傳導熱阻；Rha為散熱器與環境之間的對流熱阻圖1 結-環境熱網絡基本模型Fig.1 Basic model of junction-environment thermal network

該熱網絡模型可表示為

(1)

對式(1)進行離散化處理，得到該熱網絡模型的離散表達式為

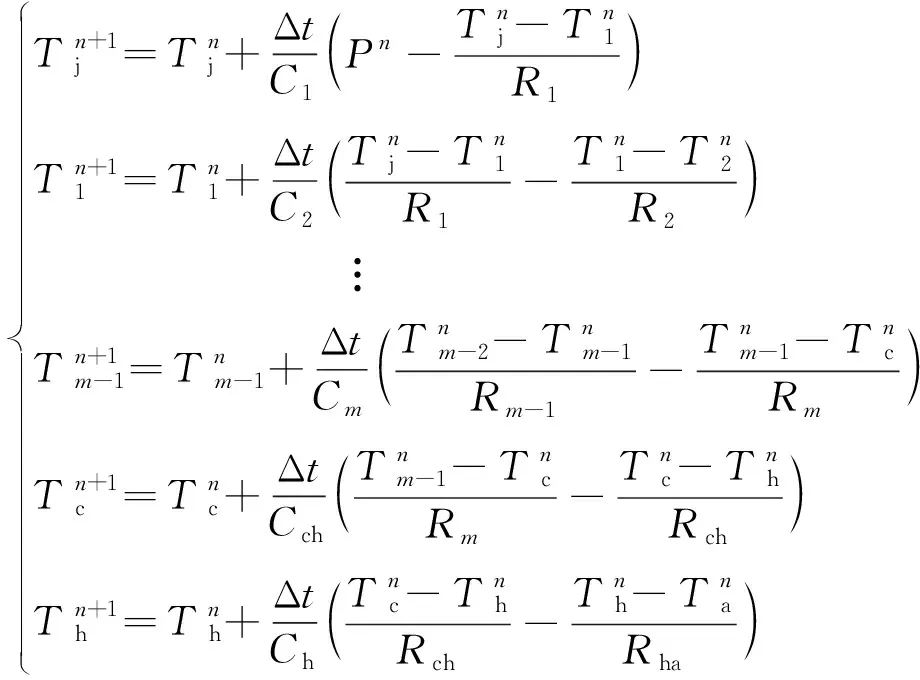
(2)

由式(2)可見，當獲得模型中損耗、熱容和熱阻等熱參數后，再結合環境溫度Ta測量值，便可有效估計任意時刻下的器件結溫Tj。

1.2 模型熱參數的確定

熱網絡模型中，器件損耗P是一個重要輸入參數，主要由功率器件及其反并聯二極管產生的通態損耗及開關損耗組成，相關計算方法與公式可參見文獻[11-12]。結-殼熱網絡中的各熱容C1～Cm和熱阻R1～Rm等參數可通過器件廠家提供的數據手冊中獲得。盡管由于器件個體差異和老化程度影響，手冊提供的熱參數會存在一定誤差，但其精度仍可滿足大部分實際工程需要。

殼-環境熱網絡中的Cch、Ch、Rch和Rha等熱容及熱阻參數計算公式為

Cch=cchmch

(3)

Ch=chmh

(4)

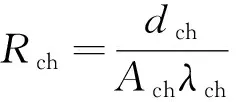
(5)

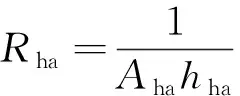
(6)

式中：cch和mch分別為殼與散熱器之間導熱材料的比熱容和質量；ch和mh分別為散熱器的比熱容和質量；dch、Ach和λch分別為殼與散熱器之間導熱材料的厚度、面積和導熱系數；Aha和hha分別為散熱器的散熱面積和換熱系數。

2 基于熱約束的功率器件散熱器成本最小化方法

2.1 功率器件的熱約束

工程中，一般利用器件結溫的最大值Tjmax及熱時間常數τ來評價其熱安全性。其中，最大值Tjmax是指器件在最大工作電流和保守散熱環境下的最高結溫，直接決定器件在極端條件是否會出現過溫現象。由于器件在開關頻率下的結溫波動通常遠小于其最大溫升，故在散熱設計階段可忽略結溫的高頻波動[13]。此時，器件最大結溫Tjmax可近似為穩態結溫。依據式(2)可知，Tjmax的計算表達式為

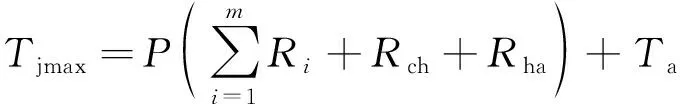
(7)

式(7)中:Ri為結-殼中第i階節點溫度。

熱時間常數τ是指器件結溫變化到最終溫度63.2%時所需的時間，表征了器件溫升速率，影響著器件老化壽命。器件結-殼材料和導熱材料分別具有質量小和導熱系數高的特點，對熱時間常數影響較小。因此，器件結溫變化的熱時間常數主要由其散熱器熱容和熱阻參數決定，即

τ=ChRha

(8)

結合式(4)和式(6)，式(7)和式(8)可分別改寫為

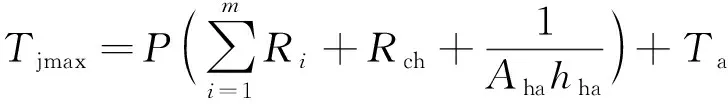
(9)

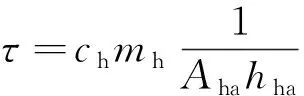
(10)

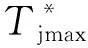
(11)

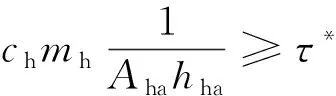
(12)

2.2 目標函數

為了最小化器件散熱器成本，需要明確相關成本函數。一般情況下，散熱器成本與質量和散熱面積呈正比關系。其中，質量決定著物料成本，散熱面積決定著加工工藝成本。為了便于分析，本文假設散熱器成本與質量mh和散熱面積Aha呈線性關系，即

C=amh+bAha

(13)

式(13)中：C為散熱器成本；a和b分別為散熱器質量與面積成本系數。

上述成本函數較為簡單，但不影響對所提方法思想的有效性驗證。未來實際應用時，也可將人工費、能耗費和廢品率等因素考慮在成本函數中。

依據式(11)～式(13)，可在器件熱約束下，構造散熱器成本最小化的目標函數J：

(14)

令x1和x2為待優化變量，且有x1=mh，x2=Aha,則目標函數可改寫為一般形式：

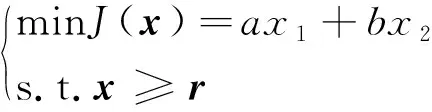
(15)

式(15)中：x=[x1,x2]T為待優化變量組成的向量；而r=[r1,r2]T為不等式約束向量，且有

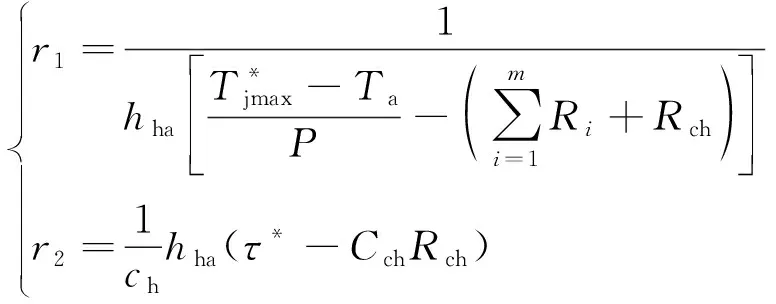
(16)

2.3 優化解法

式(15)和式(16)表明散熱器成本最小化問題本質為一個非線性優化問題。考慮到原對偶內點法是一種高效的非線性優化求解方法[14-17]，故利用該方法求解所提目標函數。

根據原始對偶內點法原理，式(15)所示目標函數存在拉格朗日函數：

(17)

式(17)中：z為拉格朗日乘子向量，z=[z1,z2]T，且有z>0；μ為障礙因子；s為非負的松弛變量向量，s=[s1s2s3s4]T；si為第i個松弛變量，i∈[1,4]。

再利用優化求解所需的一階KKT(Karush -Kuhn-Tucker)條件，可得如下兩個方程組：

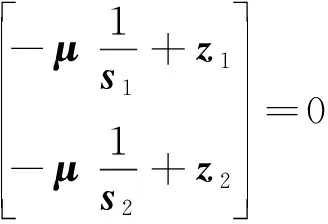
(18)

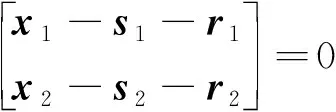
(19)

對式(18)和式(19)進行計算，最終尋找到滿足收斂條件的全局最優解，完成成本優化目標值的求解。

3 實例分析與驗證

3.1 分析對象

以型號為IRFB4410PbF型功率MOSFET和5個常用的小型散熱器為對象，對本文所提方法開展實例分析與驗證。表1給出了數據手冊中提供的功率MOSFET熱網絡模型參數；圖2和表2分別給出了散熱器的外形結構和規格參數。

表1 熱網絡模型中部分階參數Table 1 Partial orders parameters in thermal network model

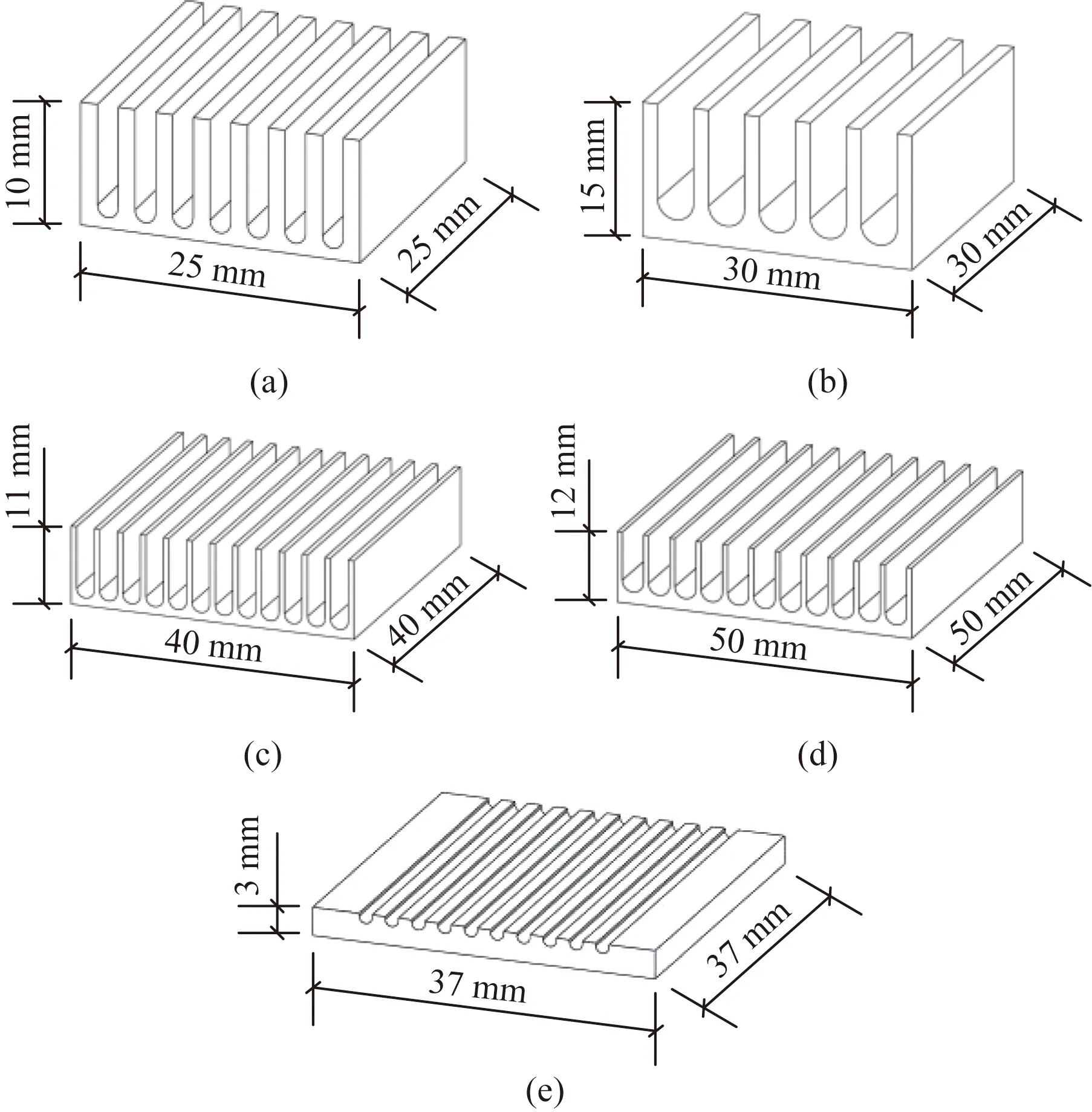
圖2 常用的小型鋁型材功率器件散熱器Fig.2 Power device heatsinks for common miniature aluminum profile

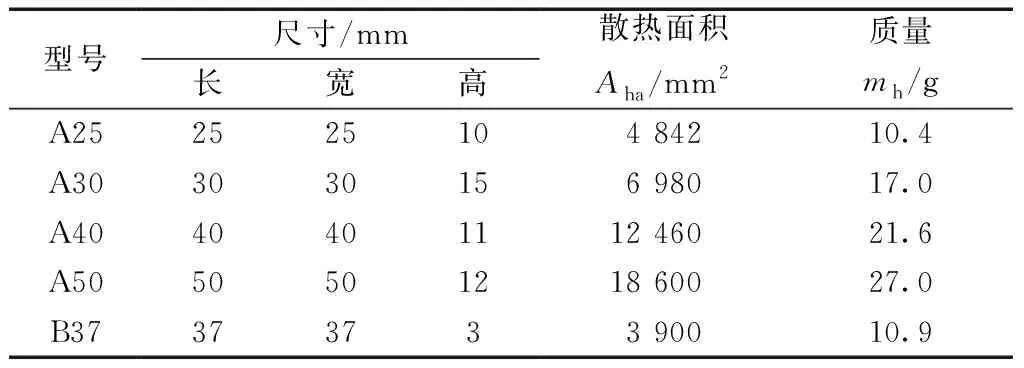
表2 散熱器規格參數Table 2 Specification parameters of heatsinks

3.2 驗證與分析

經市場調研，散熱器質量成本系數a和面積成本系數b分別可選取為15 元/kg和25 元/m2。由此可得各散熱器生產成本，如表3所示。

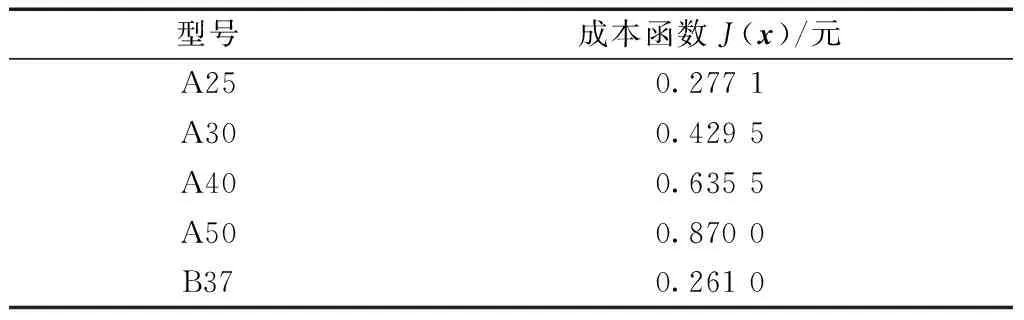
表3 各散熱器生產成本Table 3 Production cost of each heatsink

表4 散熱器優化結果Table 4 Optimization results of heatsink

根據表4可知，A40型散熱器與優化所得散熱器參數最為接近。為對此結論進行驗證，基于熱網絡模型對不同散熱器下的功率器件結溫進行估計，所得結果如圖3所示。

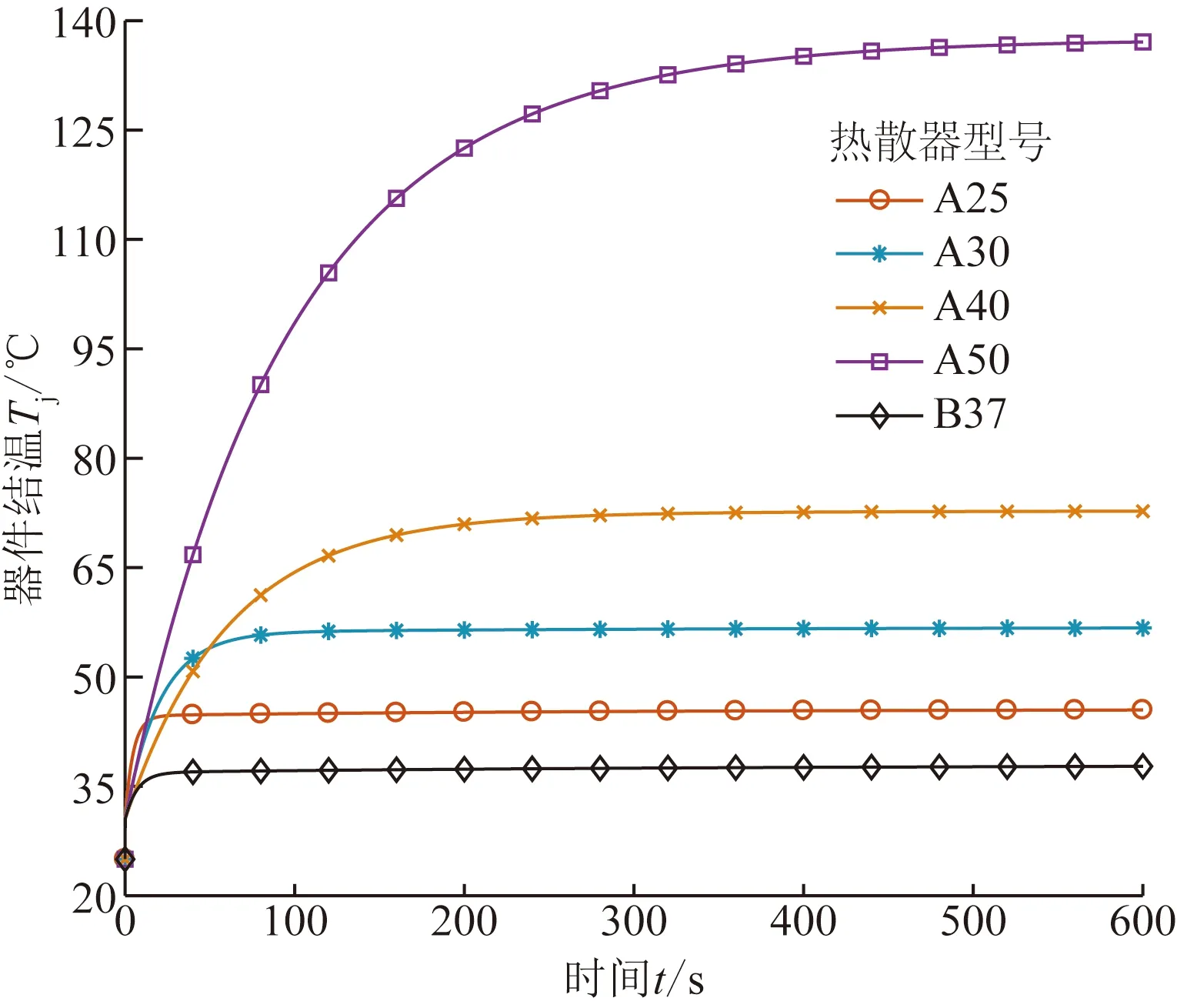
圖3 不同散熱器結溫上升過程Fig.3 Temperature rise process of different heatsinks

依據圖3所示結果，可得不同散熱器下的功率器件結溫最大值及熱時間常數，如表5所示。表中數據分析可見，加裝A40型散熱器后，器件結溫最大值僅為72.780 5 ℃，熱時間常數可達131.276 2 s，均可滿足熱約束要求。而A25、A30及B37型散熱器則無法滿足器件結溫最大值約束要求。盡管A50型散熱器同樣可以滿足器件最大結溫和熱時間常數的約束要求，但其成本卻高于A40型散熱器。因此，A40是在成本最小目標和熱約束下的最佳散熱器型號。這表明了本文優化結果的正確性。

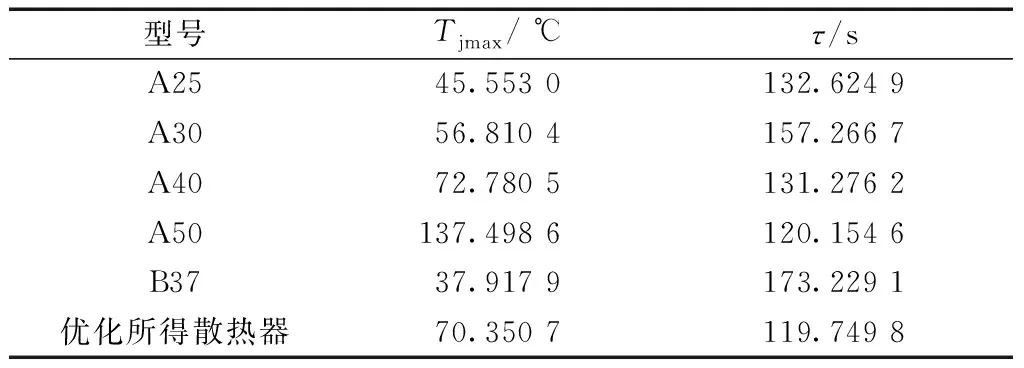
表5 優化所得散熱器與常用規格散熱器熱安全性參數Table 5 Thermal safety parameters of Optimized heatsink and common specification heatsinks

表6 不同實例分析中的最大允許結溫和最小熱時間常數設定值Table 6 The setting values of maximum allowable junction temperature and minimum thermal time constant in different case studies

表7給出了不同熱安全約束條件下的散熱器優化結果。表8給出了最接近優化結果的散熱器型號及相應熱安全性參數。結合圖3、表3、表7和表8可知，B37、A30、A50分別為三個實例分析中的最佳散熱器型號。其他類型散熱器或不滿足熱約束，或具有較高成本。上述結果表明了本文所提散熱器成本最小化方法的有效性，能夠為散熱器設計和選型提供有效依據。

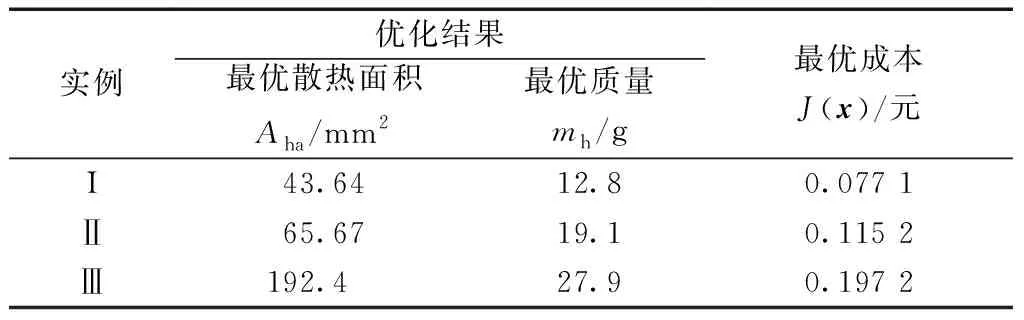
表7 不同實例分析中散熱器的優化結果Table 7 The optimization results of heatsink in different case analyses

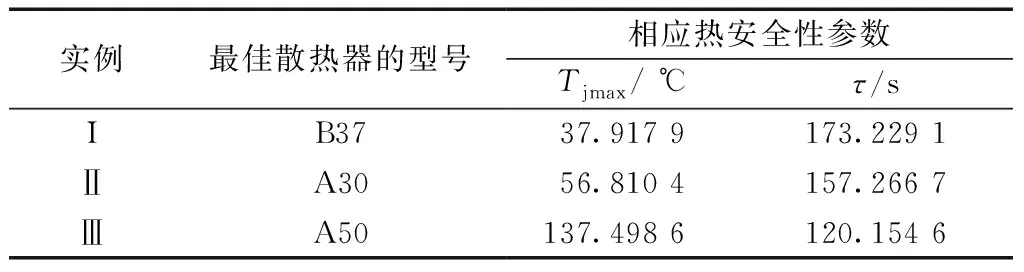
表8 不同實例分析中最佳散熱器選型及相應熱安全性參數Table 8 The best heatsink selection and corresponding thermal safety parameters in different case analyses

4 結論

結合結-環境熱網絡模型，提出了一種基于熱約束的功率器件散熱器成本最小化方法。實例分析結果表明，所提方法能夠以器件最大結溫和熱時間常數為熱安全約束量，通過非線性優化算法，找尋最佳的散熱器質量和散熱面積參數，使散熱器成本最小化，為功率器件散熱器的設計和選型提供了重要依據。此外，盡管選擇了成本相對低廉的小型散熱器開展研究，但所提方法并不受散熱器規格限制，可用于中大型規格散熱器的成本優化中。未來將在復雜和隨機散熱環境下，開展散熱器成本優化的實驗研究，以進一步提升所提方法的工程適用性。