城市無人機毫米波通信網絡建模與性能分析

衛海超， 劉銘岳， 張家紅， 許愛德

(大連海事大學信息科學技術學院， 大連 116026)

無人機具有視距通信概率高，覆蓋范圍大和可靈活部署的優點，近年來,在廣泛的應用場景中發揮重要作用[1]。例如，在有重大賽事發生的熱點地區，用戶對通信的需求量可能會在短時間內激增，無人機可以作為一種快速部署的臨時基站或空中中繼，幫助地面蜂窩網絡卸載一部分流量，提高服務質量[2-3]，或在現代軍事戰爭中，作為備份通信系統的中繼節點部署在戰場中[4]。為了研究無人機通信如何影響蜂窩通信，目前已有一些文獻研究了無人機通信網絡的性能[5-8]。其中，為了研究大規模網絡場景下無人機通信性能，諸多研究采用隨機幾何的理論工具對無人機空間分布特性進行提取建模，并加以理論分析。文獻[5]提出了一種無人機基站協助地面基站協作提供服務的下行通信系統，其中無人機基站和地面基站在水平面上的投影位置分別服從兩個獨立的泊松點過程(poisson point process, PPP)，推導了典型用戶分別與無人機基站和地面基站建立通信連接的概率，進一步推導得出了系統覆蓋率，結果顯示存在最優無人機部署高度使系統覆蓋率最大化。文獻[6]將由地面微基站和空中基站中組成的雙層網絡分別建模為泊松點過程和二項式點過程(binomial point process, BPP)，并引入了一個包含視距(line-of-sight, LOS)和非視距(non-line-of-sight, NLOS) 的信道概率模型，推導出了系統覆蓋率和頻譜效率。文獻[7]提出了一種城市地區無人機通信網絡的模型，考慮城市環境中密集的建筑物對通信鏈路的遮擋，服務無人機的選擇遵循接收功率最大化原則，而非以距離最近無人機來服務，進一步推導了該模型下的系統覆蓋率。文獻[8]考慮到無人機作為空中基站時在空間上的多層結構，當小尺度信道衰落分別為伽馬分布和指數分布時，分別推導了對應的典型小區中的系統覆蓋率的閉式表達，進一步推導出了頻譜效率，結果顯示存在最優無人機部署密度使頻譜效率最大化。

然而，以上研究中，無人機的通信頻段均為微波頻段。隨著5G時代的到來，人們對無線通信業務的需求呈指數式增長，頻譜資源匱乏的問題日趨嚴重。毫米波頻段(30～300 GHz)具有豐富的尚未開發利用的頻譜資源，是未來無線通信的必然選擇。然而，毫米波傳輸損耗嚴重，高路損，大氣衰減和雨衰減嚴重限制了毫米波信號的傳輸距離。而無人機由于具有動態部署的特性，在通信過程中可以作為毫米波通信技術的絕佳搭載平臺。例如，將無人機搭載毫米波雷達進行輸電線路巡檢[9]和植物保護中測量高度[10]等工作。綜上可見，將無人機與毫米波技術結合以彌補毫米波的固有缺陷，是未來具有前景的無線通信技術之一。

對于毫米波技術和無人機通信相結合的通信場景，文獻[11]提出了一種通用性的3D空間框架，來建模在未被基站覆蓋區域，用戶將信息發送給無人機中繼，無人機飛行到基站覆蓋區域再將信息進行轉發的毫米波通信網絡。但是無人機的飛行過程會造成通信時延，不適用于及時通信。文獻[12]針對災害應對等需要在有限區域內部署固定數量無人機的場景，將無人機的位置建模為有限區域內的二項式點過程(BPP)，構建了一種三維平面內無人機支持的毫米波網絡模型。文獻[13]提出了一種通用性的3D空間模型來建模毫米波網絡中無人機到用戶的下行鏈路，其中假設無人機裝備3D天線陣列，天線陣子通過調整方位角和仰角改變天線功率增益，進而影響系統性能。文獻[14]考慮了5G集中化無線接入網(centralized radio access network, C-RAN)架構對分布單元和中央單元分開獨立部署的要求，利用無人機搭載分布單元，與部署在地平面上的中央單元建立前傳鏈路時的性能進行了分析，對比了該架構工作在毫米波和微波頻段時的中斷概率

現有研究中，文獻[11-12]對城市地區的無人機毫米波網絡建模時，將系統的視距鏈路概率建模為關于仰角的函數，然而，這種建模方法無法分析建筑物的某一特定屬性(如高度、密度、水平尺寸、方向、位置等)對視距鏈路概率的影響。為了分析單一特性對無人機網絡的影響，文獻[13-14]將城市中的建筑物建模為無人機到用戶的水平連線上均勻分布的點，利用幾何關系推導得到該模型的視距鏈路概率，進一步分析了系統性能。然而，這種建模方法一方面忽略了建筑物的水平尺寸和方向對視距概率的影響，另一方面也沒有體現城市中建筑物位置分布的隨機性。文獻[7]提出了一種考慮了建筑物自身屬性影響的微波波段的無人機通信網絡模型，但毫米波波段固有的高路損特性使得該模型及對應的理論結果不適用于毫米波網絡。受到這些啟發，綜合考慮城區建筑物分布特性與毫米波傳輸特性，現提出一種城市地區無人機輔助的毫米波網絡模型，并基于提出的模型推導出覆蓋率的近似表達式；綜合考慮無人機配備定向天線陣列彌補毫米波的高路損，以及城市中建筑物在尺寸、高度、方向上具有的隨機性對毫米波網絡系統性能的影響。推導的理論結果可用于評估指定環境參數下無人機毫米波網絡的系統性能，以期對未來實際無人機中繼的部署具有先驗指導意義。

1 系統模型

1.1 網絡模型

選取處于建筑物的3D環境下的無人機無線通信網絡作為研究對象，其系統框架如圖1所示。首先考慮城市中的建筑物，一般地，假設城市中的建筑形狀通常為長方體結構，它們的水平尺寸、高度和方向都是隨機的、相互獨立的，中心點構成一個2D平面上的均勻的泊松點過程，強度為λB。假設每個建筑物的長L和寬W的分布服從特定的概率密度函數fL(y)和fW(y)，其期望分別為E[L]和E[W]。建筑物的方向角用φ來表示，在(0,2π]上均勻分布。建筑物的高度hB服從瑞利分布，其概率密度函數為

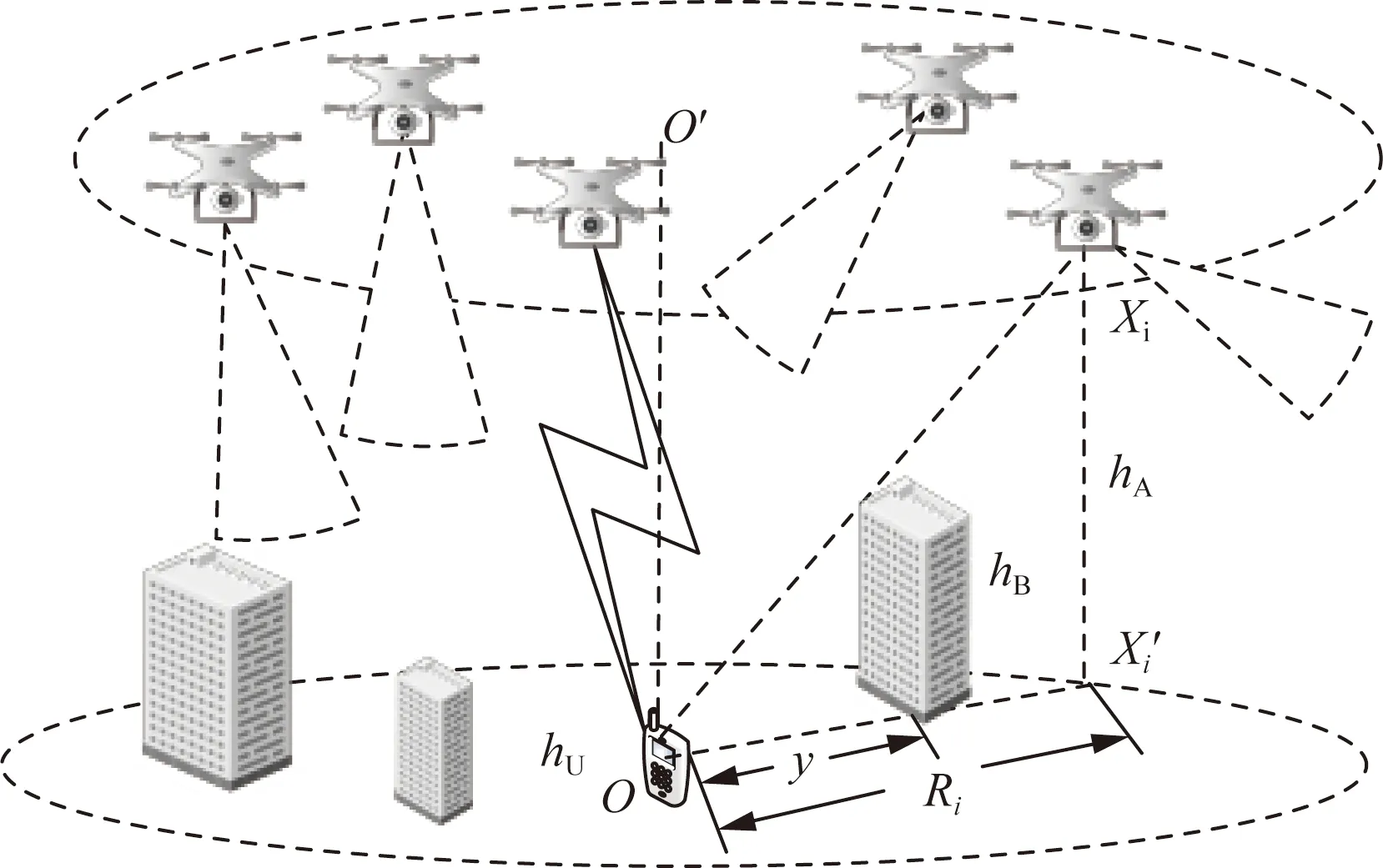
hA為無人機高度;y為建筑物到用戶的距離;X′i為無人機在水平面上的投影;hB為建筑物高度;Ri為無人機i到用戶的水平距離;O為用戶位置;hU為用戶高度;Xi為無人機的位置;O′用戶在無人機平面上的投影圖1 系統模型Fig.1 System model

(1)

式(1)中：σ為瑞利分布的尺度參數。

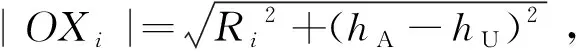
1.2 天線模型

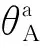
(2)

式(2)中：ζi(i=1,2,3,4)為G的分布概率；p1、p2分別為無人機端和用戶端的天線主瓣對齊的概率。用下標c∈{A,U}表示無人機端和用戶端，則

(3)

(4)

Gc=Nc,c∈{A,U}

(5)

(6)

1.3 信道模型

綜合考慮毫米波信道的大尺度衰落項和小尺度衰落項。由路徑損耗造成的大尺度衰落可以表示為(d)=d-α，其中d為無人機到用戶的距離，α為信道的路徑損耗指數。

假設1假設位于毫米波通信鏈路上的建筑物對毫米波信號完全阻擋，即毫米波不能穿透建筑物。

假設2小尺度衰落信道為Nakagami信道，信道功率增益為一個伽馬隨機變量z，其概率密度函數為

(7)

式(7)中:m為Nakagami信道的形狀因子(shape factor);Γ(m)為m的伽馬函數。

Γ(m)=(m-1)!

(8)

2 性能分析

由于系統中無人機和用戶均裝配定向天線，與干擾的功率相比，系統內的環境噪聲可以忽略不計。因此只考慮用戶端接收到的信干比(signal-to-interference ratio, SIR)作為性能評估的參數。在3D網絡模型及對應的假設條件下，下行鏈路中典型用戶接收到的信干比可以表示為

(9)

式(9)中：R0、Ri分別為典型用戶到服務無人機和干擾無人機i的水平距離；Si為OXi鏈路上的建筑物造成的總穿透功率損耗；z0、zi分別為服務鏈路和干擾鏈路的小尺度衰落項。干擾可以表示為

(10)

則覆蓋率可以進一步表示為

PCOV(T)=P(SIR>T)=Ex[P(SIR>T)]=

(11)

式(11)中：fR(x)為典型用戶到無遮擋且距離最近的無人機的距離的概率密度函數;T為接收端能正確解調信號的信干比門限。

由于無人機到用戶的小尺度衰落信道為Nakagami信道，即功率增益z0為服從伽馬分布的隨機變量。令

w(x)=mTG1-1[(hA-hU)2+x2]α/2

(12)

則式(11)可以進一步推導得到式(13)。

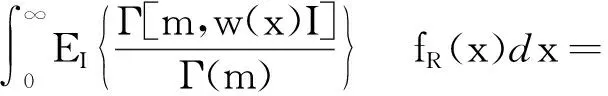
fR(x)dx

(13)

式(13)中：Γ[m,w(x)I]為上不完全伽馬函數。

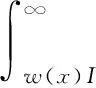
(14)

2.1 距離的概率分布

引理1根據本文3D遮擋模型，典型用戶到距離最近的可視無人機的距離x的概率密度函數[7]為

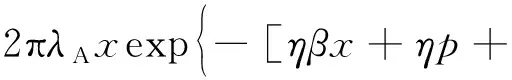
(15)

式(15)中：

(16)

p=λBE[L]E[W]

(17)

(18)

g(x)=1-(ηβx+1)e-ηβx

(19)

證明：由文獻[16]可知，位于OX′通信鏈路上的建筑物數量K′為泊松隨機變量，且滿足

E[K′]=βR+p

(20)

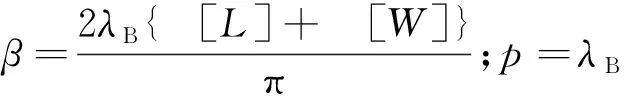
如圖1所示，考慮一個建筑物位于OX′鏈路上，距離點O的距離為y。由幾何關系易證，該建筑物只有當其高度hB>[yhA+(R-y)hU]/R時，才會對OX之間的通信鏈路造成遮擋。因此，已知一個建筑物位于OX′上，建筑物的高度服從瑞利分布，則其對OX造成遮擋的條件概率可以表示為

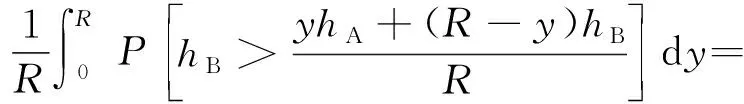
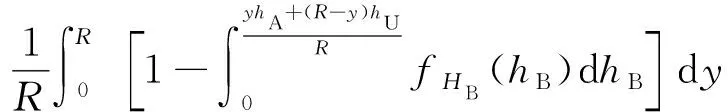
(21)

令s=y/R代入式(21)得

(22)

因此，由細化準則，對鏈路OX造成遮擋的建筑物數量K是泊松隨機變量，其期望為E[K]=ηE[K′]=η(βR+p)。由假設1，建筑物不可被穿透，則總穿透損耗為伯努利隨機變量，其概率分布為

P(Si=0)=e-η(βR+p)

(23)

P(Si=1)=1-e-η(βR+p)

(24)

不失一般性地，假設用戶位于原點O，點O′為用戶在無人機平面上的投影。則可以看出，用戶與距離最近的可視無人機的距離R大于某個值x，當且僅當所有位于圓C(O′,x)范圍內的無人機與用戶之間的鏈路被遮擋時實現。由泊松點過程的定義可以得到無人機數量的概率分布為

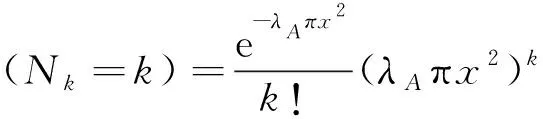
(25)

定義事件M為沒有視距通信無人機位于圓C(O′,x)內。由全概率公式，可推得典型用戶到距離最近的視距無人機的水平距離的互補累積分布函數為

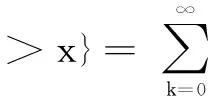
(26)

使用ex的泰勒展開式，式(26)可以進一步推導，得

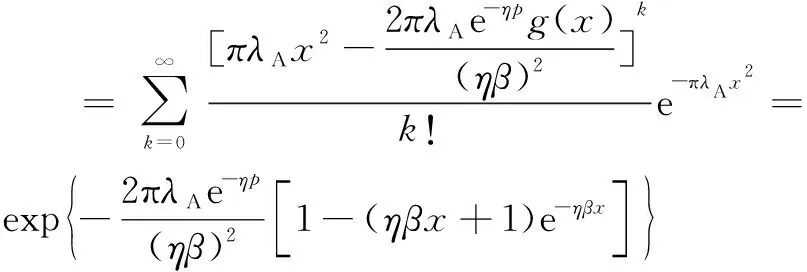
(27)

因此，距離的概率密度函數fR(x)可以通過對式(27)求導數的相反數，得

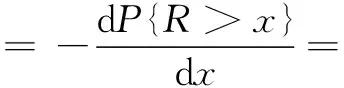
(28)

2.2 覆蓋率分析

雖然式(13)中不完全伽馬分布的互補累積分布函數可以通過對總干擾求拉氏變換，然后進行數值積分的方法計算得到，但是伽馬分布的形狀參數m越大，不同階導數所需要的計算復雜度也越高。為了便于分析，因此，給出更容易計算的表達式來近似評估系統的覆蓋率性能。

定理1當典型用戶與服務無人機的水平距離R0為x時，其條件覆蓋率可以近似表示為

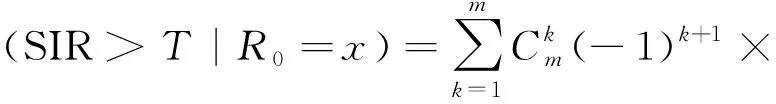
(29)

式(29)中：

(30)

(31)

(32)

證明 ：從文獻[17]可知伽馬分布存在如下不等關系:

(33)

式(33)中：

(34)

將式(33)代入式(13)，可以推導條件覆蓋率的上界為

P[SIR>T|R0=x]=

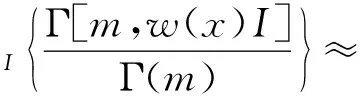
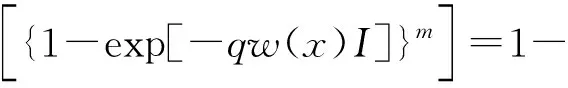
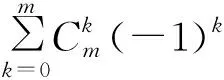
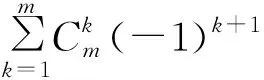
(35)

式(35)中：

EI{exp[-kqw(x)I]}=

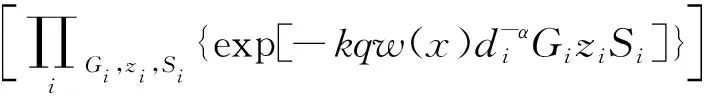
(36)

式(36)中：Si為參數為e-η(βRi+p)的伯努利隨機變量[6]，由其矩量母函數(moment generating function, MGF)可以推導得

EGi,zi{exp[-kqw(x)di-αGizi]e-η(βRi+p)+

1-e-η(βRi+p)}

(37)

因為Gi的概率分布為式(2)，利用伽馬隨機變量zi的矩量母函數，式(37)通過齊次泊松點過程的概率生成函數(PGFL)可以進一步推導得

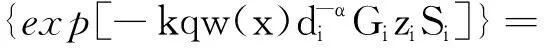
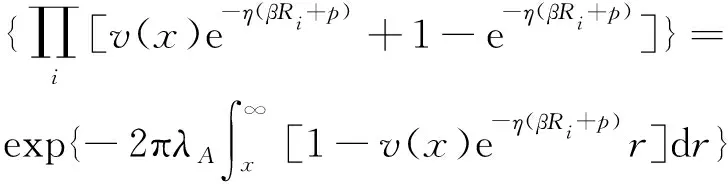
(38)

式(38)中：積分下限r是因為最近的干擾源位于距離用戶r以外。將式(38)代入式(35)，可得到條件覆蓋率的上限近似式(29)。

3 仿真驗證

本節給出毫米波無人機網絡在城市地區的覆蓋率數值仿真結果，其中，數值結果通過理論公式計算得到，仿真結果通過蒙特卡洛法得到。未經說明時，系統參數默認設定如表1所示。

表1 仿真參數Table 1 Simulation parameters

圖2為理論結果與仿真結果具有較好的近似效果。隨著無人機裝備的天線陣列陣子單元個數的增加，同一SIR門限T對應的用戶的覆蓋率也隨之提升。這是由于無人機端天線陣列陣子數量的增加，使發送端的天線增益變大，接收端收到的有用信號總增益也隨之增大，雖然干擾無人機的信號增益也增大了，但是由于定向天線的主瓣寬度很窄且隨機指向，由式(2)計算可知，當天線陣子數由4增加到32時，干擾無人機發送端與下行用戶接收端的主瓣波束對齊的概率由5.8×10-3減小到7.2×10-4，因此，干擾增益對用戶覆蓋率性能的影響遠遠小于有用信號增益的。此外，從圖2可以看出，當SIR的門限T取值為0 dB時，不同天線陣子數量下的覆蓋率都接近1，這說明對服務質量要求較低的地區(即較低的SIR閾值)，可以減少部署在該地區的無人機的天線陣子數量，這樣可以在不影響系統性能的情況下，降低運營商成本。而當SIR的閾值等于10 dB時，不同天線陣子數量對應的覆蓋率表現出明顯差異，天線陣子數為4和8的系統，對應的覆蓋率只有0.6和0.8，所以為了滿足服務質量要求較高的地區，無人機攜帶天線的天線陣子數量應該不小于16。

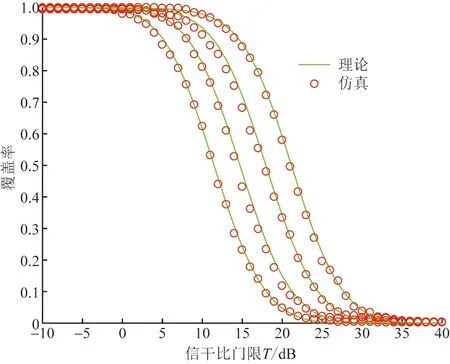
圖2 不同天線陣子數量的覆蓋率Fig.2 The coverage probability for different number of antenna elements

圖3顯示了在建筑物密集地區，覆蓋率與無人機高度之間的關系。給定信干比門限T=20 dB，λB=6×10-4m-2，E[L]=E[W]=30 m，NA=16。

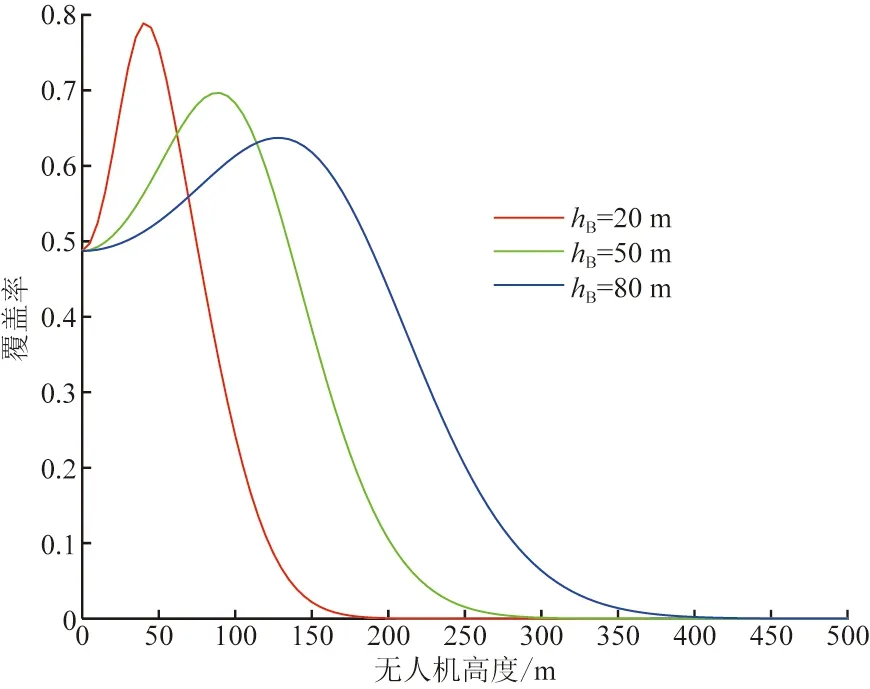
圖3 無人機高度對覆蓋率的影響Fig.3 The impact of the height of UAVs on the coverage probability

由圖3可以得出以下結論。

(1)優化無人機高度可以提升系統性能。對于圖3中任一曲線，當建筑物的平均高度固定時，用戶的覆蓋率先是隨著無人機部署高度的增加而上升，達到一個峰值后，然后開始下降。這說明存在一個無人機部署的最優高度可以使覆蓋率最大。這是因為在城市建筑物密集的地區，無人機平面的高度越高，與用戶建立視距通信鏈路的概率也越高，所以開始的時候系統性能也隨之提高。然而，當無人機達到一定高度后，路徑損耗就成為影響網絡性能的主要因素，隨著無人機和用戶之間距離的增加，覆蓋率開始下降。

(2)用戶覆蓋率的峰值隨著建筑物平均高度的增加而降低。這與建筑物越高，越容易對毫米波鏈路造成遮擋的事實相一致。

(3)針對上述環境，在建筑物比較低的區域內(即hB=20 m)，無人機部署在50 m左右時可以使系統覆蓋率最大化，而在建筑物比較高的高樓區域(即hB=80 m)，無人機需要部署在140 m左右才能使達到最大覆蓋率，且此時的覆蓋率遠小于前者。這是由毫米波的高路損特性決定的。

覆蓋率與無人機密度之間的關系如圖4所示。

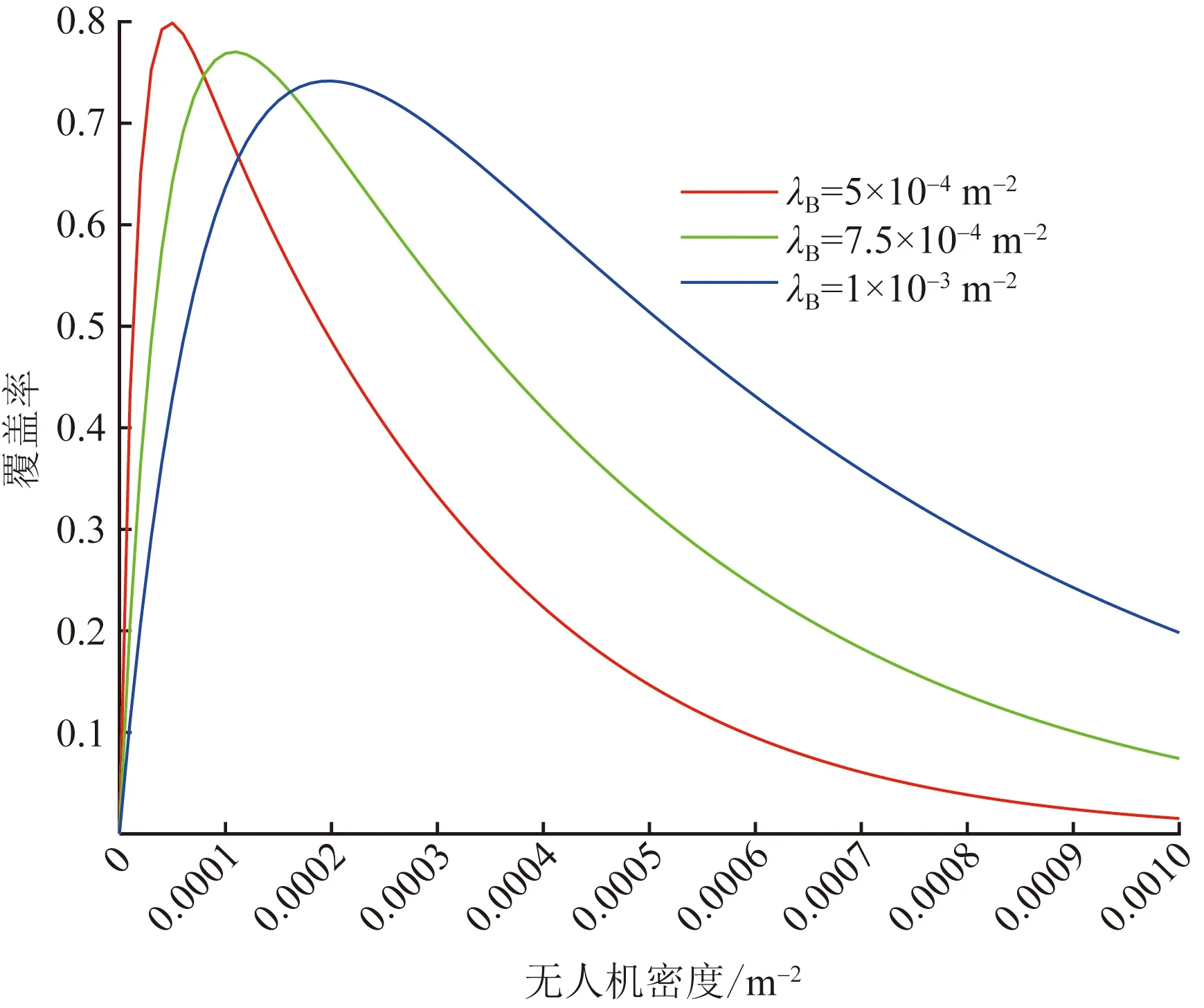
圖4 無人機密度對覆蓋率的影響Fig.4 The impact of the density of UAVs on the coverage probability

給定信干比門限T=20 dB，E[L]=E[W]=30 m，NA=16，hA=50 m。

由圖4可以得出以下結論。

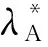
(2)隨著無人機密度增大，開始時建筑物密度越大，能達到的覆蓋率越小，這是因為此時建筑物密度的增大，導致用戶端與距離近的無人機間的通信鏈路更容易被遮擋，延長了有用信號的傳輸距離，導致覆蓋率下降。而隨著無人機密度增大，建筑物密度和覆蓋率的關系也隨之變化，到了特定閾值后，建筑物密度越大，覆蓋率也越大，這是因為當無人機密度足夠大時，建筑物遮擋住距離用戶近的無人機的概率降低，對有用信號傳輸距離的影響也隨之減小，而距離相對較遠的干擾信號仍會被建筑物遮擋，建筑物對干擾信號的抑制作用大于對有用信號的抑制作用，所以覆蓋率隨著建筑物密度的增大而升高。

(4)針對同一建筑物密度的條件下，無人機達到最優部署密度后，系統覆蓋率將隨著無人機密度的增大而迅速降低，這是由無人機的干擾信號導致的。在實際部署時需引入干擾協調等策略來降低干擾，保證用戶接收到的服務質量。

4 結論

基于隨機幾何理論，提出了一種城市地區無人機毫米波網絡的模型，考慮了建筑物的遮擋對毫米波通信鏈路的影響，并推導了對應的下行鏈路典型用戶的覆蓋率近似表達式。經過仿真驗證，近似表達式和仿真結果的誤差很小。進一步分析了系統各個參數對覆蓋率性能造成的影響。得到以下結論。

(1)在服務質量要求低的區域，即使減少無人機天線陣子數量,也可滿足服務需求，同時降低運營商成本。而在對服務質量要求高的地區，無人機攜帶天線陣子數量應盡可能多。

(2)存在最優無人機部署高度和密度,使相同條件下的系統覆蓋率達到最大。建筑物越高，分布越密集，系統能達到的最大覆蓋率越小。

(3)無人機在超過最優部署密度后，覆蓋率會隨著無人機密度的增大而迅速衰減，為了提高服務質量，需要引入干擾協調等策略來抑止接收端接收到的干擾信號。