統(tǒng)一潮流控制器并聯(lián)變換器虛擬慣量控制策略

張海同， 王金梅， 袁小威， 何 銘， 鮑振鐸

(寧夏大學物理與電子電氣工程學院， 銀川 750021)

靈活交流輸電(flexible AC transmission system, FACTS)技術(shù)在電力系統(tǒng)中的應用日漸廣泛，統(tǒng)一潮流控制器(unified power flow controller，UPFC)作為第3代柔性交流輸電FACTS裝置的代表，是迄今為止功能最為全面的FACTS裝置[1-3]；作為串、并聯(lián)結(jié)合的控制器，能有效地進行線路的潮流控制[4]、無功功率補償及電壓的動態(tài)調(diào)節(jié)[5-7]，在提高電能質(zhì)量和改善輸電系統(tǒng)穩(wěn)定運行方面等方面發(fā)揮著非常重要的作用[8-10]。

在電力系統(tǒng)潮流控制時，需要維持UPFC接入點電壓和UPFC內(nèi)部直流電容電壓恒定，從而提高電力系統(tǒng)穩(wěn)定性，否則會導致電壓偏移較大或者UPFC停機從而影響電力系統(tǒng)。文獻[11]對于電網(wǎng)在新能源高滲透率下虛擬慣量逐漸不足問題，建立虛擬慣量分配模型，提出改進的演化算法對慣量進一步優(yōu)化配置，與傳統(tǒng)算法相比，其尋優(yōu)性能較好、精度較高。文獻[12-13]提出了新的電容電壓平衡控制策略，前者在傳統(tǒng)電容電壓平衡控制策略基礎(chǔ)上進了改進，引入了虛擬同步機技術(shù)和載波移項調(diào)制，提高系統(tǒng)虛擬慣量和阻尼系數(shù),保持電壓穩(wěn)定；后者利用卡爾曼濾波特性結(jié)合電流解耦合脈沖補償控制，實現(xiàn)電容電壓平衡，改善控制系統(tǒng)動態(tài)性能。文獻[14]從調(diào)節(jié)線路潮流的角度出發(fā)，將線路有功無功潮流作為系統(tǒng)輸入量，來提高控制效果，由于控制器延遲，使得其動態(tài)特性略差；文獻[15]研究了一個真實的多區(qū)域多源的模型，以飛蛾火焰優(yōu)化算法為優(yōu)化工具，以UPFC為運載調(diào)控器，抑制負載擾動時振蕩，增強系統(tǒng)魯棒性；文獻[16-17]詳細分析了UPFC串并聯(lián)側(cè)變換器有功、無功的交互影響，以及交互影響程度與控制器間的耦合程度的關(guān)系；文獻[18]提出了極坐標系下新型功率解耦控制策略，采用串聯(lián)側(cè)變換器有功功率-相位、無功功率-電壓的控制方法，維持功率平衡；文獻[19]通過改進飛蛾撲火算法，建立基于UPFC的電網(wǎng)控制優(yōu)化模型，優(yōu)化后的控制參數(shù)，進一步增強系統(tǒng)對電壓支撐能力。

綜上所述，針對UPFC系統(tǒng)在潮流調(diào)節(jié)時的接入點電壓和直流電容電壓波動的問題，現(xiàn)提出基于虛擬慣量的UPFC并聯(lián)變換器控制策略，通過引入UPFC電容虛擬慣量，設(shè)計虛擬慣量控制器，來降低潮流控制過程中的電壓波動，改善系統(tǒng)對電壓的支撐能力；為進一步加快控制速度，提出了一種改進前饋補償點的控制方法，將改進的前饋量引入到并聯(lián)變換器控制環(huán)路中，來改善功率協(xié)調(diào)控制效果，提高系統(tǒng)響應速度；以期為進一步降低電力系統(tǒng)潮流控制時的電壓波動提供理論基礎(chǔ)。

1 UPFC數(shù)學模型

UPFC主要由變壓器以及兩個電壓源型變換器通過直流電容背靠背聯(lián)接而成，由于變換器接入線路方式不同分為并聯(lián)變換器和串聯(lián)變換器。圖1是UPFC結(jié)構(gòu)圖。

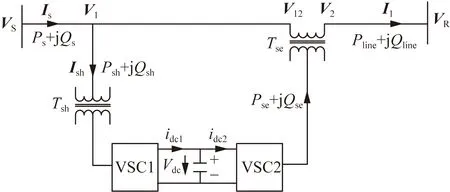
VS和VR分別為線路首端、末端電壓矢量；V1和V2為UPFC接入兩端線路電壓矢量；V12為串聯(lián)側(cè)注入補償電壓矢量；Vdc為直流側(cè)電容電壓；Is和I1分別為線路首端輸入電流、線路電流矢量；Ish為并聯(lián)側(cè)變換器輸入電流矢量；Ps+jQs為線路首段輸送功率；Pline+jQline為線路末端輸送功率；Psh+jQsh為并聯(lián)側(cè)與線路交換功率；Pse+jQse為串聯(lián)側(cè)交換功率；idc1和idc2分別為并聯(lián)側(cè)變換器輸出電流、串聯(lián)側(cè)變換器輸入電流；VSC1和VSC2分別為變換器1、變換器2圖1 UPFC結(jié)構(gòu)圖Fig.1 UPFC structural diagram

UPFC串、并聯(lián)變換器數(shù)學模型[8]可表示為

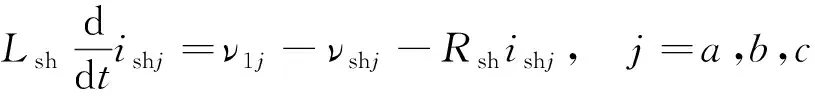
(1)

(2)

式中：Lsh、ish、νsh和Rsh分別為并聯(lián)側(cè)線路電感、并聯(lián)變換器輸出電流、并聯(lián)變換器輸出電壓和并聯(lián)變換器等效內(nèi)阻。Lse、ise、νse和Rse分別為串聯(lián)側(cè)線路電感、串聯(lián)變換器輸出電流、串聯(lián)變換器輸出電壓和串聯(lián)變換器等效內(nèi)阻。

為了方便控制，三相電壓需作dq旋轉(zhuǎn)坐標變換，將電網(wǎng)電壓ν1定向于d軸方向，變換矩陣為

(3)

式(3)中：ω為角速度。

式(1)和式(2)通過變換矩陣，可得dq旋轉(zhuǎn)坐標系下串并聯(lián)變換器數(shù)學模型為

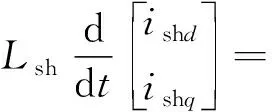
(4)

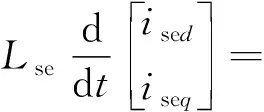
(5)

并有

式中：ishd和ishq分別為并聯(lián)側(cè)變換器輸入電流d、q軸分量；ν1d和ν1q分別為電網(wǎng)電壓d、q軸分量；ised和iseq分別為串聯(lián)側(cè)變換器輸出電流d、q軸分量；νsed和νseq串聯(lián)側(cè)變換器輸出電壓d、q軸分量。

通過式(4)、式(5)可以看出，無論是并聯(lián)變換器還是串聯(lián)變換器，它們的有功無功電流分量id和iq都存在強烈的耦合現(xiàn)象。因此，為了達到線性化控制目標，非常有必要設(shè)計合理的解耦控制系統(tǒng)。

將并聯(lián)變換器dq坐標系下數(shù)學模型進行變化，式(4)可表示為

(6)

令

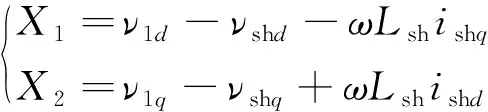
(7)

可得解耦后并聯(lián)變換器的數(shù)學模型：

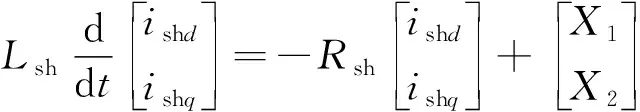
(8)

由式(8)可知，通過調(diào)節(jié)X1和X2來達到對有功無功電流解耦的控制目標。

2 并聯(lián)變換器控制策略

2.1 并聯(lián)變換器穩(wěn)壓控制最

根據(jù)功率平衡原理，在穩(wěn)壓控制系統(tǒng)直流電容電壓控制過程中引入d軸有功電流前饋量；在UPFC接入點電壓控制過程中引入q軸無功電流前饋量。

由功率平衡原理可知：

Psh=PshR+Pdc

(9)

Pdc=Pse+PseR

(10)

式中：Psh、PshR和Pdc分別為并聯(lián)變換器有功功率、并聯(lián)變換器內(nèi)部消耗功率、直流電容交換功率，Pse和PseR分別為串聯(lián)變換器有功功率、串聯(lián)變換器內(nèi)部消耗功率。

假設(shè)電網(wǎng)電壓三相對稱，根據(jù)對稱性得

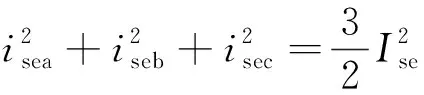
(11)

由式(11)可推出串聯(lián)變換器的瞬時有功功率：

(12)

式(12)中：φ為電壓V12與電流Ise的相位差。

已知：

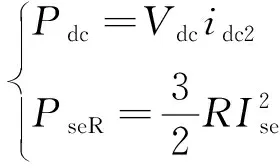
(13)

將式(12)和式(13)代入式(10)中，可得

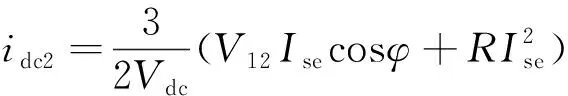
(14)

由于PseR?Pse，因此可以忽略前者的影響，式(14)可化簡為

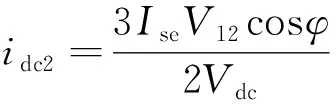
(15)

式(15)可變化為

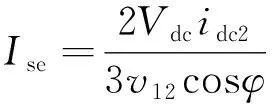
(16)

將式(16)進行坐標變換，可得穩(wěn)壓控制系統(tǒng)有功電流前饋量：

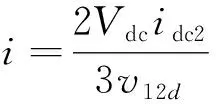
(17)

同理可得，穩(wěn)壓控制系統(tǒng)無功電流前饋量：

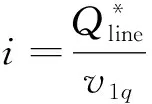
(18)

因此，通過在并聯(lián)變換器穩(wěn)壓控制系中引入有功電流前饋量和無功電流前饋量，實現(xiàn)功率的協(xié)調(diào)控制，降低直流電容電壓和UPFC接入點電壓的偏移，提高動態(tài)響應。

2.2 UPFC的虛擬慣量控制策略

在UPFC系統(tǒng)中，直流電容的作用極其重要，既能給串、并聯(lián)變換器提供良好的通路進行有功功率的交換，也能進行濾波和支撐直流電容電壓。當UPFC內(nèi)部的有功功率平衡被打破時，直流電容電壓也隨之變化，此時直流電容進行充電或放電，即對能量的儲存或釋放，類似于同步機轉(zhuǎn)子。模擬前者特性，引入UPFC電容的虛擬慣量。即

(19)

式(19)中：Ec、H、SUPFC分別為直流電容儲存能量、UPFC電容的虛擬慣量和UPFC容量。

通過圖1可得電容功率平衡方程：

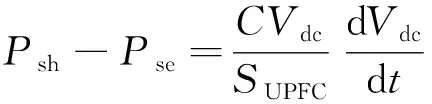
(20)

又同步機轉(zhuǎn)子運動方程為

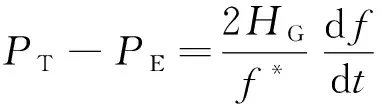
(21)

式(21)中：PT、PE分別為原動機機械功率和同步機電磁功率；HG、f*、f分別為同步機慣量、系統(tǒng)設(shè)定頻率和系統(tǒng)實際頻率。

通過觀察式(20)和式(21)可知，兩個式子的結(jié)構(gòu)和表達形式具有相似性，直流電容對能量的吸收和釋放類同于同步電機轉(zhuǎn)子吸收和釋放能量一樣，前者只是直流電容能量的改變與直流電容電壓變化的關(guān)系，后者是同步電機轉(zhuǎn)子能量的改變與系統(tǒng)頻率變化的關(guān)系。所以建立直流電容電壓和系統(tǒng)頻率的關(guān)系，用直流電容電壓的變化來反映系統(tǒng)頻率的變化，使兩者緊密相連。

因此由式(20)和式(21)可以變形得

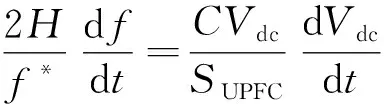
(22)

式(22)中：H為UPFC的虛擬慣量。

將式(22)進行積分變換：

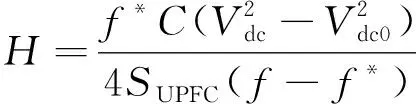
(23)

式(23)中：Vdc0為直流電容電壓初始值。

將式(23)變形可得

(24)

以上分析可得，含有虛擬慣量的UPFC并聯(lián)變換器控制系統(tǒng)如圖2所示。

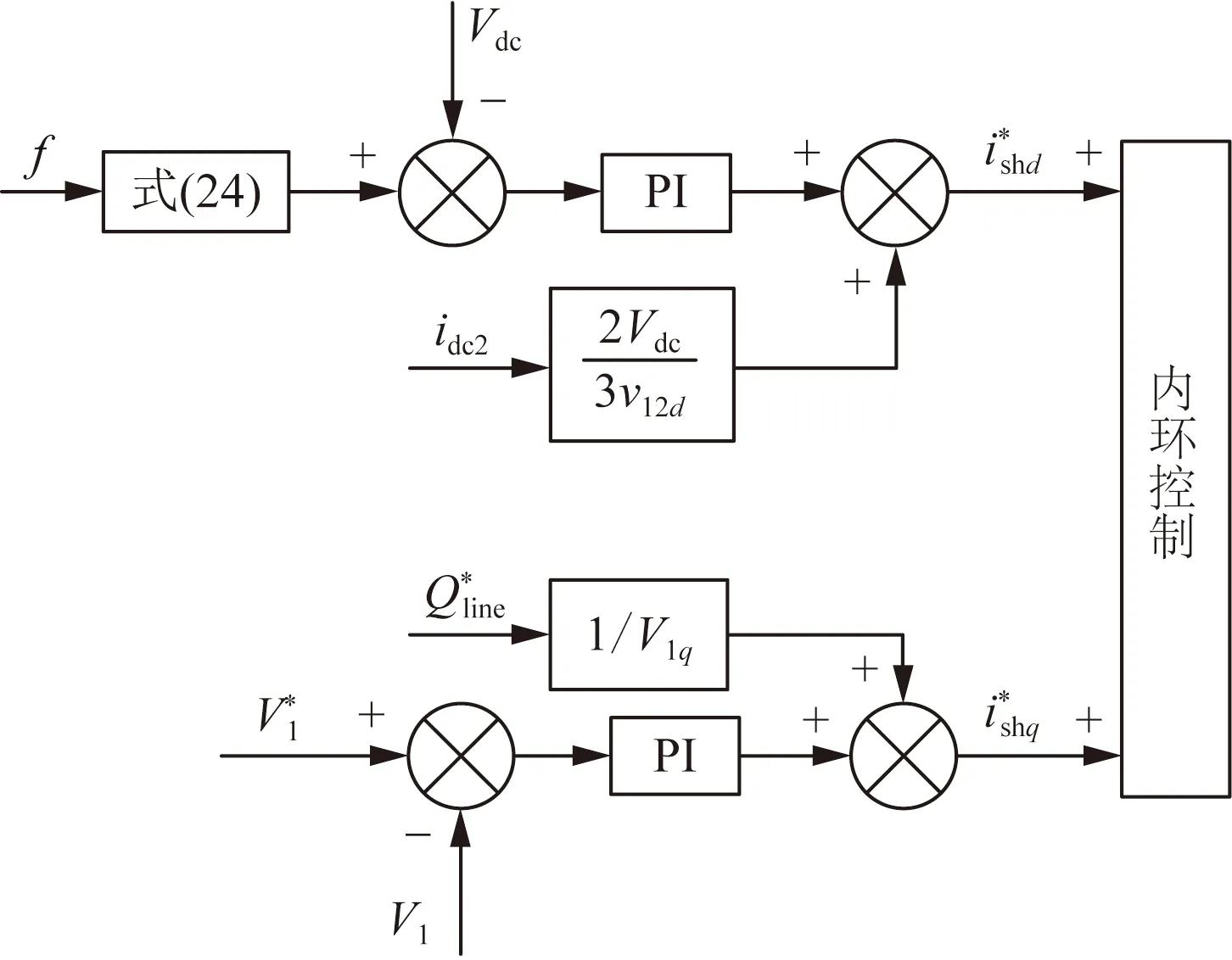
ν* 1和分別為電網(wǎng)電壓設(shè)定值、線路無功設(shè)定值；PI為比例積分控制器圖2 含有虛擬慣量的UPFC并聯(lián)變換器控制系統(tǒng)Fig.2 Control system of UPFC parallel converter with virtual inertia

通過在UPFC并聯(lián)變換器電壓外環(huán)的基礎(chǔ)上，設(shè)計虛擬慣量控制器，并且以系統(tǒng)實際頻率響應為輸入量，從而調(diào)節(jié)直流電容電壓；通過虛擬慣量，使得系統(tǒng)響應得以改善，提高UPFC系統(tǒng)對電壓的支撐能力。

2.3 改進前饋的控制策略

由于在控制系統(tǒng)中存在電感的影響和PI(proportional integral)控制器的延遲，無法進行電流的實時補償，會使得控制效果降低，因此將d軸有功分量控制環(huán)路和q軸無功分量控制環(huán)路做出改進。

UPFC并聯(lián)側(cè)d軸有功分量控制環(huán)路如圖3所示。

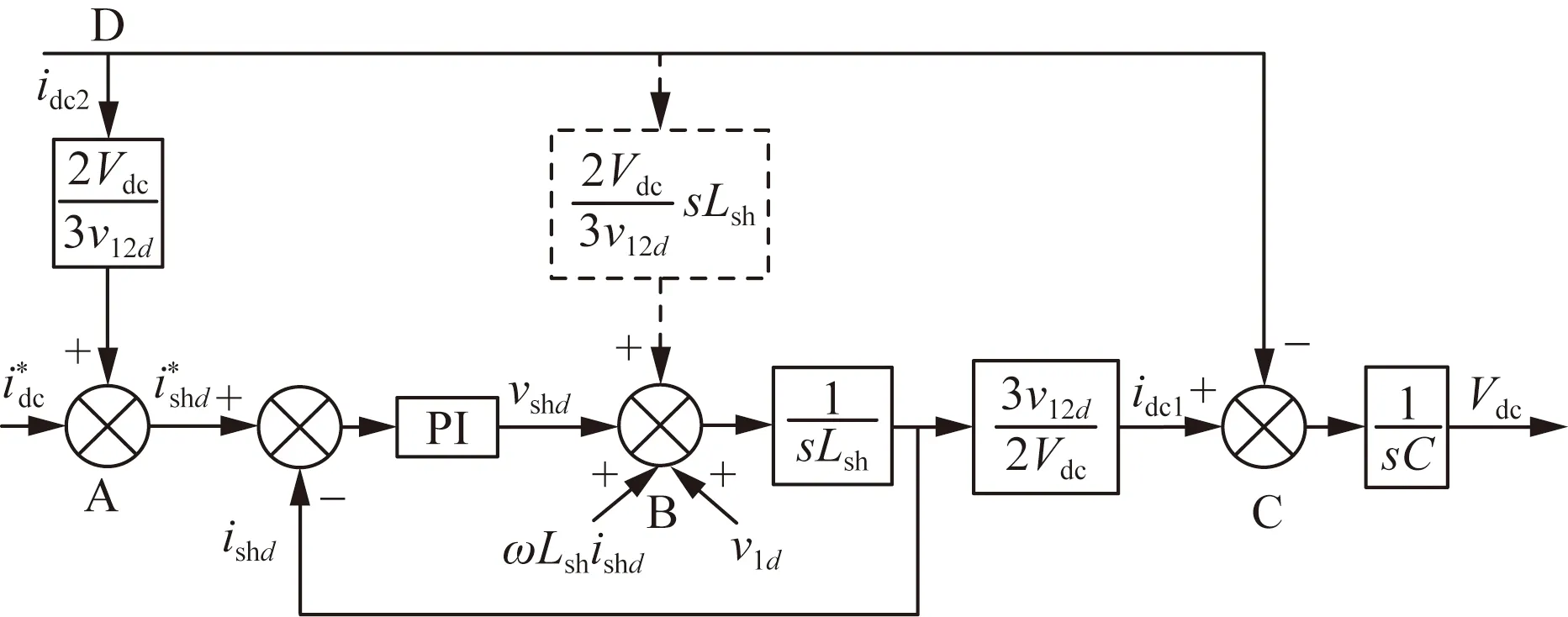
圖3 d軸有功分量控制環(huán)路Fig.3 d-axis active component control loop

由圖3可知，從節(jié)點D到節(jié)點C傳遞函數(shù)為

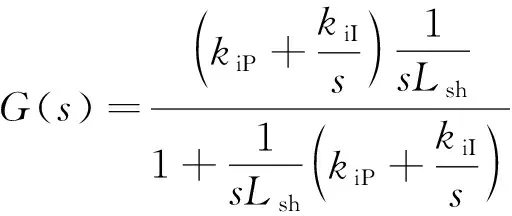
(25)

式(25)中：kiP、kiI分別為UPFC并聯(lián)變換器電感電流比例、積分系數(shù)。

分析式(25)可知，只有當Lsh無窮小，增益無窮大時，從節(jié)點D到節(jié)點C的傳遞函數(shù)才會為單位1。實際情況卻并非如此，為了保證電流濾波的基本要求，Lsh也不可能無窮小；而且又考慮到PI控制器的穩(wěn)定，增益也不可能取得無窮大。基于以上因素影響，使得idc2跟蹤idc1有一定延遲，導致直流電容電壓產(chǎn)生大幅波動。因此，將d軸有功分量控制環(huán)路做出了以下改進，如圖3中虛線所示，將前饋補償點從A點右移至B點，引入電感和微分；降低PI控制器和電感對前饋的影響。

改進后，從節(jié)點D到節(jié)點C傳遞函數(shù)為

(26)

由式(26)可知，改進后的傳遞函數(shù)為單位1，能夠?qū)崿F(xiàn)電流的無差別實時補償。

UPFC并聯(lián)側(cè)q軸無功分量控制環(huán)路如圖4所示。

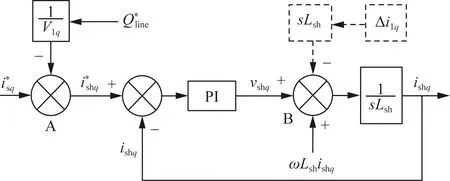
圖4 q軸無功分量控制環(huán)路Fig.4 q-axis reactive component control loop

3 仿真驗證

為了驗證所提控制策略的有效性，設(shè)計兩種工況來進行實驗驗證。工況1：線路潮流控制(改變輸電線路潮流設(shè)定值時，系統(tǒng)動態(tài)響應)；工況2：三相短路(在含有UPFC的仿真輸電系統(tǒng)中，將串聯(lián)變換器調(diào)控的負載處進行三相短路連接)；運用MATLAB搭建UPFC仿真模型。系統(tǒng)仿真控制參數(shù)如表1所示。

表1 UPFC仿真參數(shù)Table 1 UPFC simulation parameters

3.1 工況1：潮流控制

UPFC系統(tǒng)控制的線路有功功率和無功功率初始值分別為5.87、-0.27 p.u.，仿真時間為20 s，在第2 s時UPFC切入，UPFC虛擬慣量H為0.704 s。

圖5為有功功率設(shè)定值改變時線路潮流仿真波形圖，觀察圖5可知，線路有功功率初始值為5.87 p.u.，6 s時設(shè)置為6.87 p.u.，第14 s時又恢復至初始值，且在1 s內(nèi)迅速保持穩(wěn)定，設(shè)定值改變前后，有功調(diào)節(jié)都有著較好的響應速度；潮流調(diào)節(jié)過程中，有功潮流的變化對無功潮流影響甚微。

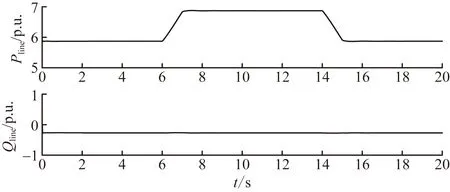
圖5 有功設(shè)定值改變時線路潮流波形圖Fig.5 Waveform diagram of line flow when the active power setting value changes

圖6為無功功率設(shè)定值改變時線路潮流仿真波形圖，由上圖可知，線路無功功率初始值為-0.27 p.u.，6 s時設(shè)置為-0.17 p.u.，第14 s時又恢復至初始值，在0.2 s內(nèi)迅速保持穩(wěn)定，設(shè)定值改變前后，無功調(diào)節(jié)有著較快的響應速度；潮流調(diào)節(jié)過程中，無功功率的變化對有功潮流影響甚微。

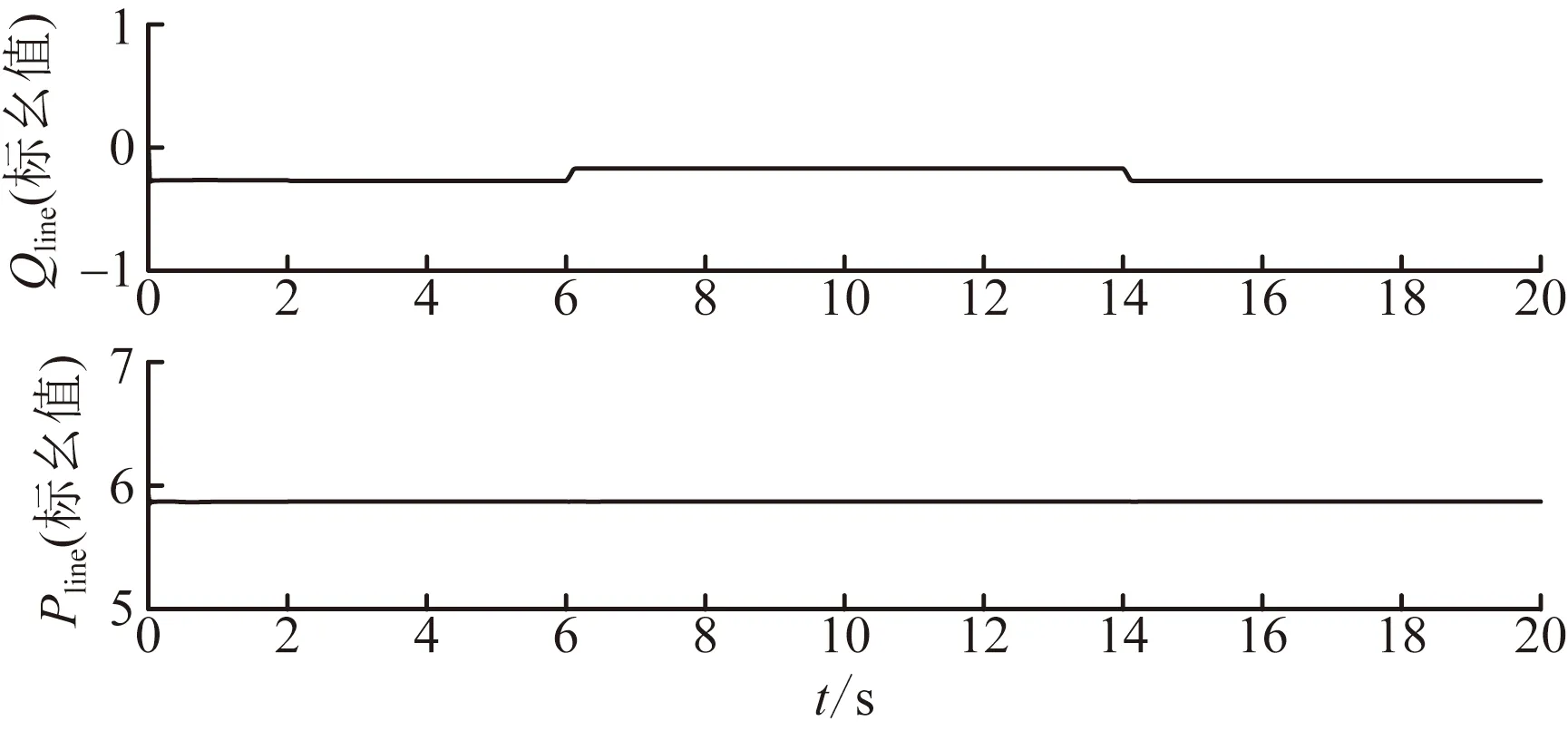
圖6 無功設(shè)定值改變時線路潮流波形圖Fig.6 Waveform diagram of line flow when reactive power setting value changes

通過上文分析可知，在采用了本文控制策略下，UPFC系統(tǒng)仍然有著較好的潮流調(diào)節(jié)能力，可以達到有功無功獨立調(diào)控的要求。

常規(guī)控制策略、本文控制策略下并聯(lián)側(cè)接入點電壓仿真波形如圖7和圖8所示。

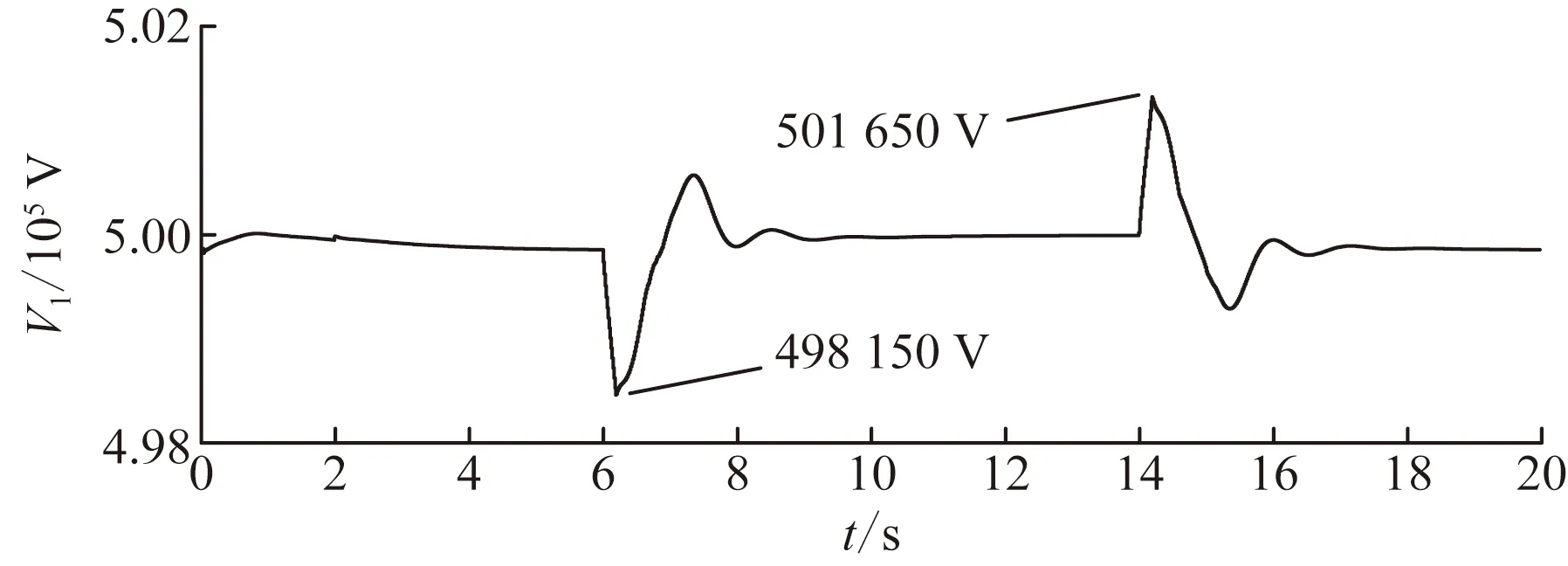
圖7 常規(guī)控制策略下并聯(lián)側(cè)接入點電壓Fig.7 The Voltage of parallel access point under conventional control strategy

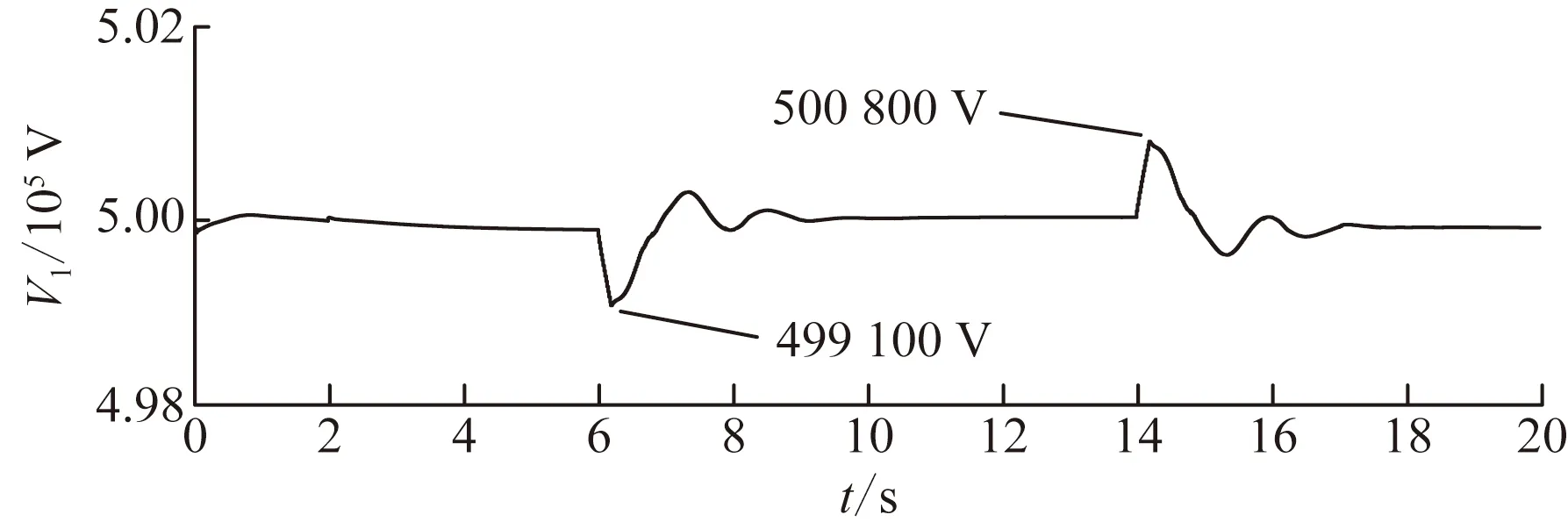
圖8 文中控制策略下并聯(lián)側(cè)接入點電壓Fig.8 The voltage of parallel access point under the control strategy in this paper

通過圖7和圖8可以看出，在采用文中控制方法后，并聯(lián)側(cè)接入點電壓的最大值和最小值分別由501 650、498 150 V變?yōu)?00 800、499 100 V，電壓偏移量由3 500 V減小至1 700 V，并聯(lián)側(cè)接入點電壓幅值波動范圍明顯變小。

常規(guī)控制策略、文中控制策略下直流電容電壓仿真波形如圖9和圖10所示。

由圖9和圖10可知，常規(guī)控制策略下電容電壓振蕩嚴重、波動范圍大，8.6 s時電容電壓趨于穩(wěn)定；采用文中控制策略后電容電壓最大值由40 010 V變?yōu)?0 005 V，最小值由39 990 V變?yōu)?9 995 V，電壓波動由20 V減少為10 V；8.3 s時電容電壓趨于穩(wěn)定,由于UPFC虛擬慣量，提高了UPFC系統(tǒng)對電壓的支撐，因此電容電壓振蕩次數(shù)減少，電壓波動幅值變小，電壓波動衰減時間也降低了0.3 s。

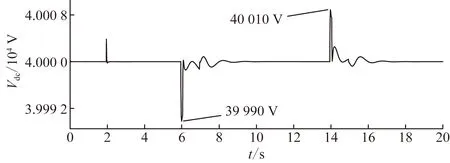
圖9 常規(guī)控制下直流電容電壓Fig.9 DC capacitor voltage under conventional control

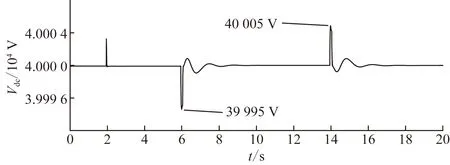
圖10 文中控制策略下直流電容電壓Fig.10 DC capacitor voltage under the control strategy in this paper

3.2 工況2：三相短路

線路有功無功初始值分別為6.87、-0.17 p.u.，仿真時間為20 s，在第5 s時UPFC切入，UPFC虛擬慣量H為0.704，在第7 s時三相故障模塊切入閉合，持續(xù)50 ms，即在第7.05 s時該模塊斷開，線路恢復正常。

圖11為在三相短路時并聯(lián)側(cè)接入點電壓仿真波形。由于三相短路故障的出現(xiàn)，線路首端電壓急速下降，末端電壓也會受到嚴重影響，因此并聯(lián)側(cè)接入點電壓也會有顯著變化。由圖11可知，常規(guī)控制策略下電壓波動較大、震蕩頻繁；然而在文中控制策略下，電壓波形起伏略緩，振蕩減少，并快速恢復至穩(wěn)態(tài)值。

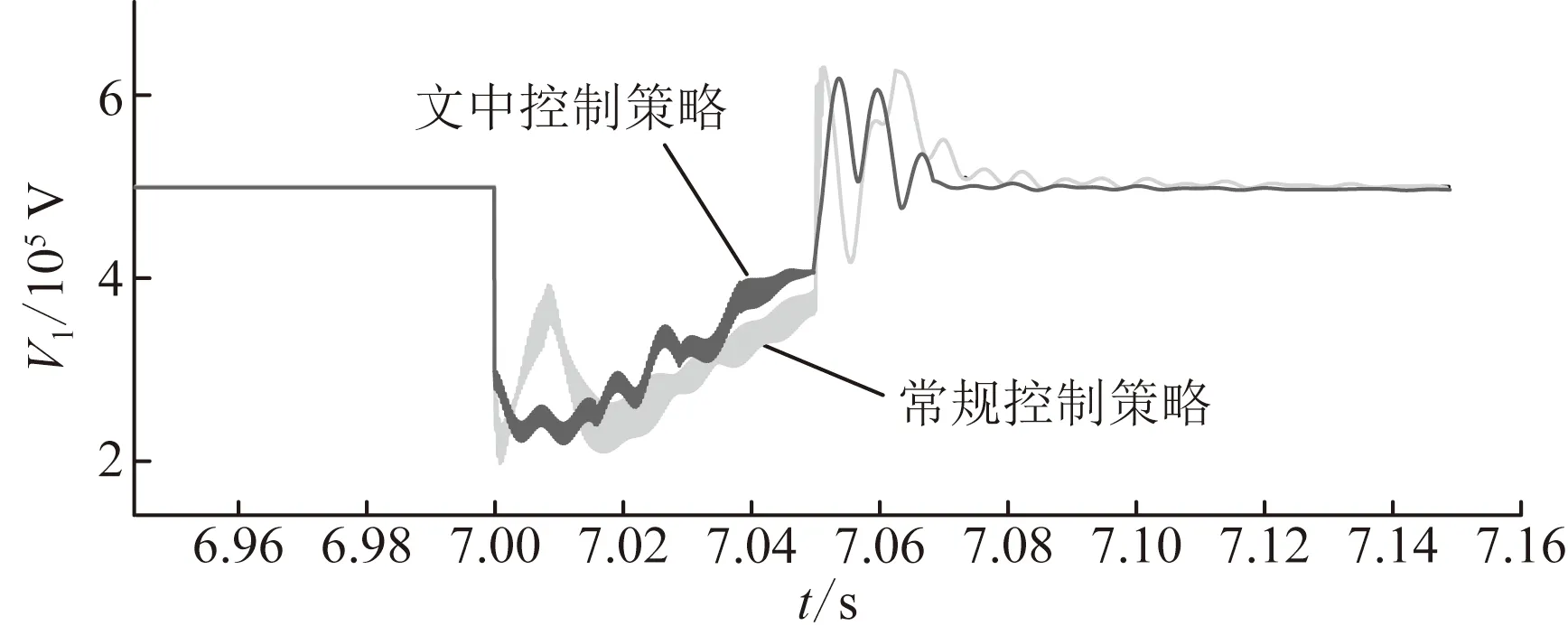
圖11 三相短路時并聯(lián)側(cè)接入點電壓Fig.11 The voltage of parallel access point under three-phase fault

圖12為在三相短路時直流電容電壓仿真波形。

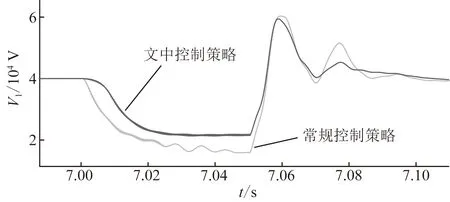
圖12 三相短路時直流電容電壓Fig.11 DC capacitor voltage under three-phase fault

由圖12可知，常規(guī)控制策略下，當系統(tǒng)發(fā)生三相故障時，電容電壓突然下降，轉(zhuǎn)折點明顯，在電容特性的支撐下有了部分時段電壓平緩下降，振蕩明顯，且在事故消除后波動較大；在文中控制策略下，當發(fā)生三相故障時，電容電壓平緩下降并快速穩(wěn)定，由于電容特性、以及電容的虛擬慣量的注入，使得系統(tǒng)對電壓的支撐能力得到有效的提升，故障消除后，電容電壓的波動、振蕩以及恢復時間也略少于前者。

4 結(jié)論

針對潮流控制過程中UPFC系統(tǒng)的接入點電壓和直流電容電壓波動的問題，引入UPFC虛擬慣量，設(shè)計了其虛擬慣量控制器，提出基于虛擬慣量的并聯(lián)變換器控制策略以及改進前饋的控制方法，來及時抑制UPFC潮流控制過程中功率不平衡的影響，提高系統(tǒng)反應速度。與常規(guī)控制策略進行了兩種工況仿真驗證對比，結(jié)論如下。

在文中控制策略下，UPFC系統(tǒng)仍有較好的潮流控制能力，該控制策略能有效地降低并聯(lián)側(cè)接入點電壓和直流電容電壓的波動，后者響應時間也降低了0.3 s，系統(tǒng)功率平衡得以提高，協(xié)調(diào)控制效果良好；當系統(tǒng)發(fā)生三相故障時，由于UPFC電容虛擬慣量的注入，使得系統(tǒng)對電壓的支撐能力也得以改善，因此，該策略能在一定程度上減少三相故障對電壓跌落程度的影響。