空水兩棲子母系統設計與研究

馬躍，李潔，唐雪，蔣海洋，王葉文

(西南科技大學四川省特殊環境機器人技術重點實驗室，四川綿陽，621000）

0 引言

進入21世紀之后海洋問題日益顯得突出，領土爭端、資源勘探、海洋污染、溫室效應等問題已經成為困擾人們的熱點問題，迫切需要具有在復雜環境搜尋功能的機器人系統。相比于單種機器人平臺，兩棲機器人具有靈活性高、適應性強、多功能運動模式等技術優勢，在目前機器人作業環境日益多元化和復雜化的情況下具有廣闊的應用前景。

目前國內外兩棲機器人的研究多采用變換推進方式實現水空工作模式切換，但大多機器人結構復雜，對于工作環境要求較高。一款由哈爾濱工業大學[1]設計的動璞明輪式兩棲機器人，采用在橡膠輪胎內側加上璞板的方式讓機器人在水中也具有前進能力。該機器人結構設計簡單，具有很強的實用性，但因其兩個運動方式同時進行，動力浪費嚴重，續航能力不足。哈佛大學在2015年設計研發了一款水空兩棲仿昆蟲機器人Robobee[2]，采用撲翼方式提供在水空流體中航行的動力，在水中和空中都具有較好的俯仰控制[3]，并具有較好的自主航行能力。但該機器人系統的供電系統具有較大的問題，不能長時間的處于工作狀態。

基于以上研究和問題，我們探索出一套空水結構與子母協作的機器人系統，具有環境適應能力強、靈活性高、工作時間長等優勢特點，可解決當前單種機器人在水、陸、空三域搜尋定位的靈活性差、適應性弱和多功能運動模式受限等問題，為國家公共安全的監測、預警與應急處理提供應用理論和技術儲備[4]。

1 系統設計

空水兩棲子母系統的設計分為子體系統和母體系統兩部分。母機器人采用水上浮球輪式機器人，主要實現水上和陸地運動，可提供大容量電源，為子機器人的續航時間提供了保障。由車艙、浮輪、主控裝置、推進裝置、釋放裝置、氣漲裝置、傳感器裝置、定位及通信裝置等部分構成。

子體系統為水空可變結構飛行器，主體為呈圓盤形的多自由度兩棲飛行器，用于滿足低空及淺域的探測，采用空中固定旋翼式螺旋槳加水中涵道式螺旋槳形式推進。系統硬件包括控制器、空中與水下動力系統、視覺系統、姿態測量系統、通信系統、電源系統等模塊。

子系統與母系統配合，組成一個工作環境適應性強、活動范圍大、便于使用等諸多優勢的空水兩棲子母搜尋定位系統。

2 運動控制器設計及仿真

2.1 機械結構設計

空水兩棲機器人的機械結構設計主要包括機身、涵道推進器及旋翼裝置三部分。其機身由機身底座和機身頂蓋通過螺釘緊固連接，并構成一完整的碟形機身[5]；其涵道推進器設置于機身外圍，對稱安裝于機身左右兩端面，并通過舵機臂與機身內部的防水舵機相連；機身表面開設六大通孔作為旋翼裝置的旋翼域，且分別穿過通孔中心設置徑向機軸，徑向機軸中部開設電機槽，電機槽內部安裝防水無刷電機，螺旋槳即安裝于防水無刷電機上方[6]。其機械結構示意圖如圖1所示。

圖1 空水兩棲機器人機械結構示意圖

2.2 運動學及動力學模型

空水兩棲機器人在空中和水下的運動過程中，會受到很多因素的影響，為了便于建立空水兩棲機器人的運動數理模型[7]，做出如下假設:

（1）空水兩棲機器人為剛體，不易形變；

（2）空水兩棲機器人的重心與機體坐標系原點相重合；

（3）空水兩棲機器人呈完全均勻對稱。

由歐拉角定義，機體坐標系和地面坐標系原點重合，地面坐標系可經過三次旋轉得到機體坐標系[8]，設飛行器相對地面坐標系旋轉的歐拉角為橫滾角φ、俯仰角θ和偏航角ψ。

首先，繞Z軸旋轉ψ，X轉到X'，Y轉到Y'，對應的旋轉矩陣為RZ,ψ。其次，繞Y'軸旋轉θ，X'轉到X''，Z轉到Z'，對應的旋轉矩陣為RY,θ。最后，繞X''軸旋轉φ，Y'轉到Y''，Z'轉到Z''，對應的旋轉矩陣為RX,φ。

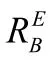
則當機體坐標系下各位置量已知時，則可根據上述規則，將其轉換到大地坐標系下：

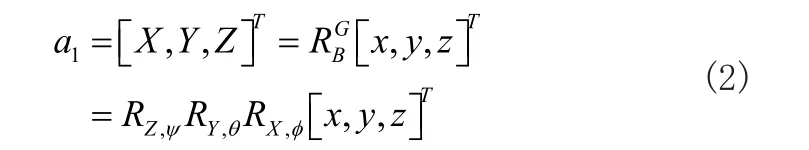
將上式等式兩邊的位置量對時間求導，可得線速度的轉換關系。同時，根據歐拉角定義橫滾角φ、俯仰角θ和偏航角ψ，進行微分幾何推導可得到角速度的轉換關系：

式中u、v、w分別表示機體沿X、Y、Z軸平動時的線速度，p、q、r分別表示機體圍繞X、Y、Z軸轉動時的角速度。將式（3）和式（4）聯立可得到空水兩棲機器人的運動學方程，如式（5）所示 ：

空水兩棲機器人的運動可以簡化為平動和轉動，平動方程滿足牛頓第二運動定律，轉動方程滿足歐拉定理。六自由度機器人動力學方程可如下式所表達：

2.3 控制器設計

本系統的控制器設計目標是實現對空水兩棲機器人的位置和姿態進行控制，而運行環境的不確定性以及存在的外界干擾等都會增加控制的復雜度。所以控設計采用了經典的PID控制模型[9]，在被控對象的模型有較多不確定性因素和外界干擾環境干擾的情況下，同樣適應性強，魯棒性好。控制器使用串級PID控制的方法，將空水兩棲機器人的控制算法分成兩個回路，構成外環位置控制回路和內環姿態控制回路，空水兩棲機器人控制模型框圖如圖2所示。

圖2 控制器設計框圖

控制器的被控對象為機體位置坐標，初始輸入為預設位置坐標，輸出目前位置坐標，兩坐標的偏差值作為反饋信號，使得對機體方向和姿態進行控制完成當前位置的修正。

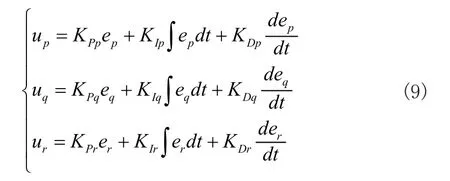
2.4 控制器仿真

為了驗證理論上控制器的相應性能，在MATLAB里建立了相應的仿真模型并對其進行了相應的仿真驗證[10]，系統位置及姿態仿真結果如圖3所示，可知控制系統穩態誤差基本為零，同時系統反應速度較快，控制器控制機體x、y、z方向上的位置與姿態，從初始狀態到達預設位置經過10s～20s即可到達穩定。

圖3 空水兩棲機器人xyz方向位置及姿態仿真曲線圖

3 結束語

本文設計了一套水空結構與子母協作的機器人系統，分別進行了母體和子體的機械結構設計和軟硬件系統設計，并且進行了空水兩棲機器人運動模型建立和控制器的設計與分析[11]，最后結合仿真結果對整個控制器的運動控制性能進行了驗證。解決了當前單種機器人在水、陸、空三域搜尋定位的靈活性差、適應性弱和多功能運動模式受限等問題，為國家公共安全的監測、預警與應急處理提供應用理論和技術儲備。