一種分數槽永磁同步電機的轉矩計算方法*

羅曉祎 張鳳閣

(沈陽工業大學電氣工程學院 沈陽 110870)

1 引言

隨著永磁電機的研究不斷深入，永磁電機的性能也在逐步提高，特別是電機的轉矩特性，它將直接影響電機的轉矩輸出能力與平穩運行能力。

傳統計算分數槽永磁同步電機轉矩的方法是利用d-q參考系中的磁鏈計算分數槽永磁同步電機的轉矩。這種計算方法未考慮磁鏈諧波和d-q軸之間的交叉互感，導致計算結果不準確[1]。

文獻[2-4]中提出了一種內置式永磁同步電機數學模型，該方法用線性磁鏈模型解釋電機在不飽和狀態下的交叉磁化，用非線性磁鏈模型解釋電機在飽和狀態下的交叉磁化，并用試驗測量了電機的磁鏈和電感。文獻[5]分析了在不同的負載下，永磁電機的氣隙磁密、反電勢、電感和轉矩脈動的變化規律，然后對6 種極槽配合電機的轉矩諧波次數進行分析、總結，得到分數槽表貼式永磁同步電機轉矩的計算方法。文獻[6]中利用電機的磁鏈來計算永磁電機的轉矩，發現當鐵心飽和度增加時，電機的轉矩脈動也會增加。然后對比了不同極槽配合下永磁電機的平均轉矩和轉矩脈動，在d-q軸下施加恒定的電流，對比24 槽4 極和24 槽20極永磁同步電機平均轉矩和轉矩脈動。文獻[7]采用繞組函數研究定子磁動勢的諧波分布，通過主波磁動勢的時空分布揭示了磁動勢和轉矩之間的關系，并分析了五相容錯永磁同步電機存在開路故障時轉矩波動變化的原因。文獻[8]利用有限元分析軟件對電機進行三維電磁場分析，運用場的方法計算出齒槽轉矩和電磁轉矩，分析外永磁轉子爪極電機極數對轉矩密度和齒槽轉矩的影響。文獻[9]提出一種基于參數化dq0 坐標變換的永磁同步電機建模方法計算出電機的轉矩，結果可用于矢量控制等。文獻[10]在電機磁路未飽和的狀態下簡化了電機在d-q軸下的數學模型，忽略電機的磁動勢諧波，計算出電機在穩態運行下的轉矩。文獻[11-12]考慮電機的飽和程度和在d-q軸下的交叉磁化，開發出有限元分析的程序，減少了有限元仿真時間。文獻[13]提出了一種基于三角函數的新型開關磁阻電機磁鏈解析模型，由此磁鏈模型推導出的轉矩公式是三角函數與多項式積分的乘積，多項式是可積分的，且計算過程簡潔。文獻[14]利用繞組函數對四種槽極配合表貼式分數槽集中繞組的永磁電機進行研究。分析了電機勵磁電感、諧波電感、槽漏感和端部電感的大小及相互關系。但文章沒有對傳統的電感計算方法進行分析，也沒有對不同槽極配合的槽漏感計算公式進行研究分析。

然而這些轉矩計算精度均不高，計算方法不具有通用性。且一個精確的數學模型可以將各個諧波轉矩及產生諧波轉矩分離出來，并揭示出轉矩諧波的來源，從而在控制電機時，可以特定消除某次轉矩諧波，這樣能夠大大提高永磁電機的控制精度，如文獻[15]通過提取電機相電流主要存在的5 次負序、7 次正序諧波交流分量，將提取的諧波交流分量注入到輸出電壓中來抑制諧波，該方法就需要一個精確的數學模型。因此本文提出了一種新的永磁同步電機轉矩計算方法，并對一臺1.5 kW 分數槽永磁同步電機的轉矩進行計算，分別計算出了電機的永磁轉矩、永磁轉矩諧波及磁阻轉矩、磁阻轉矩諧波，分析出轉矩諧波的主要來源。

利用有限元仿真計算空載反電動勢和定子電流產生的磁鏈，確定永磁轉矩諧波是由轉子磁鏈諧波與定子電流作用產生，磁阻轉矩諧波是由定子在d-q軸下的自感磁鏈諧波和互感磁鏈諧波與轉子鐵心作用產生。通過上述分析建立模型計算出分數槽永磁同步電機的轉矩，最后驗證模型的正確性。

2 永磁電機的基本參數和結構

考慮電機的轉速及運行工況，電機采用“一”字型內置式結構，通過計算確定1.5 kW 永磁電機主要結構參數，如表1 所示。

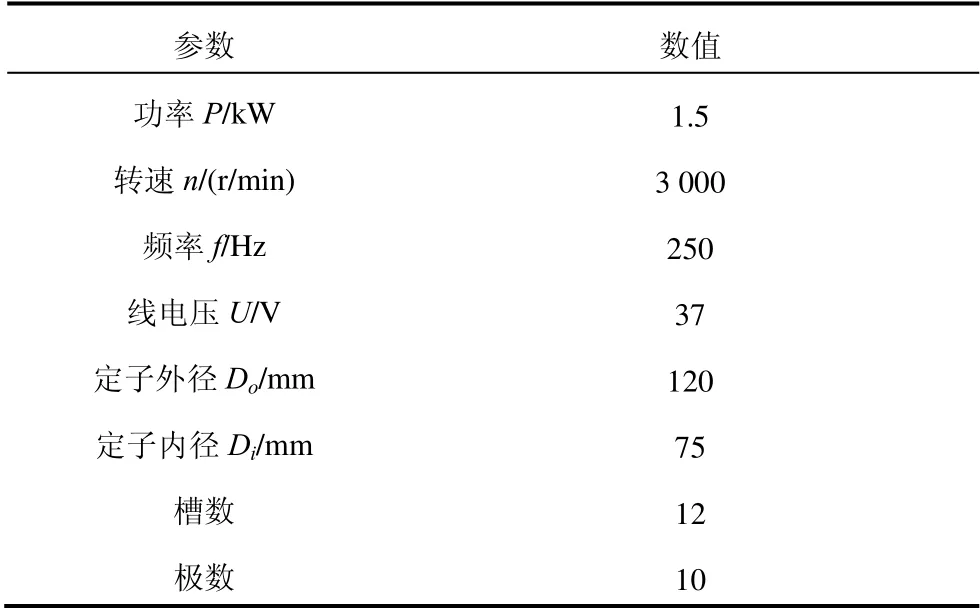
表1 1.5 kW 永磁電機的額定數據及結構參數

3 分數槽永磁電機的數學模型

3.1 經典的電機數學模型

分數槽永磁同步電機在d-q坐標系下的方程為式(1)～(6)。

式中，K是Park 變換矩陣，Vabc是相電壓，iabc是相電流，eabc是三相反電動勢，Labc是三相電感，R是電阻，Ld和Lq分別是d軸和q軸電感。同樣，id、iq、Vd、Vq分別是d-q軸的電流和電壓，Kq是電機的反電動勢常數，ωm是電機機械角速度，ωe是電角速度，p是功率。

3.2 改進的電機數學模型

通過對經典的電機數學模型進行改進，改進后的模型將轉矩分解為永磁轉矩、永磁轉矩脈動以及磁阻轉矩、磁阻轉矩脈動。永磁轉矩及永磁轉矩脈動是由轉子上的永磁體與分布在定子繞組的電流的相互作用產生，并利用反電動勢常數計算出永磁轉矩及永磁轉矩脈動。磁阻轉矩及磁阻轉矩脈動是由定子磁鏈與轉子鐵心作用產生，并利用電機自感和互感計算出磁阻轉矩及磁阻轉矩脈動。對所產生的轉矩及轉矩脈動分兩步建模，建模過程如下所示。

3.2.1 永磁轉矩及永磁轉矩脈動

考慮到永磁體產生的磁鏈諧波，此時的轉矩方程為

式中，n=6k，k=0、1、2、3、4 等。Kxm0是基波反電勢常數，Kxm6、Kxm12、Kxm18、Kxm24分別是6、12、18、24 次諧波反電動勢常數的幅值，αxm6、αxm12、αxm18、αxm24分別是6、12、18、24 次諧波的相位，x表示d軸和q軸，m表示永磁體。

3.2.2 轉子凸極產生的磁阻轉矩和磁阻轉矩脈動

由于轉子的凸極結構，使得轉子在d-q軸上的磁阻不同，導致定子磁鏈與轉子鐵心作用產生磁阻轉矩。同時考慮到d-q軸之間的交叉互感，所以改進后在d-q軸中產生的磁鏈是由自感磁鏈和互感磁鏈組成，此時磁鏈模型方程為式(12)～(13)。

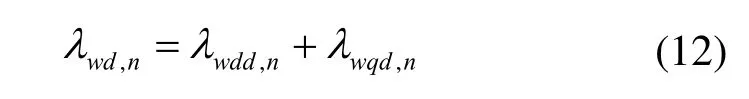
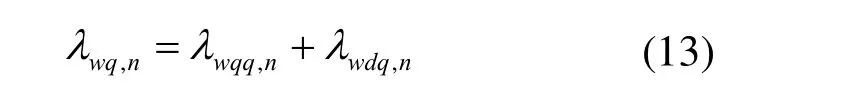
式中，n=6k，k=0、1、2、3、4。w表示由定子繞組，dd和qq分別表示d軸和q軸產生的自感磁鏈。qd表示由q軸電流在d軸產生的磁鏈，dq表示由d軸電流在q軸產生的磁鏈。

由于存在自感磁鏈和互感磁鏈，所以在d-q軸中存在基波自感Lqq,n、Ldd,n和互感Lqd,n、Ldq,n，此時磁鏈方程為

在式(21)中，公式第一項表示改進模型中電流流過電阻產生的壓降；第二項是空載反電動勢，由式(22)表示；第三項是由定子磁鏈產生的電動勢，由式(23)表示。此時電壓的等效電路如圖1 所示。

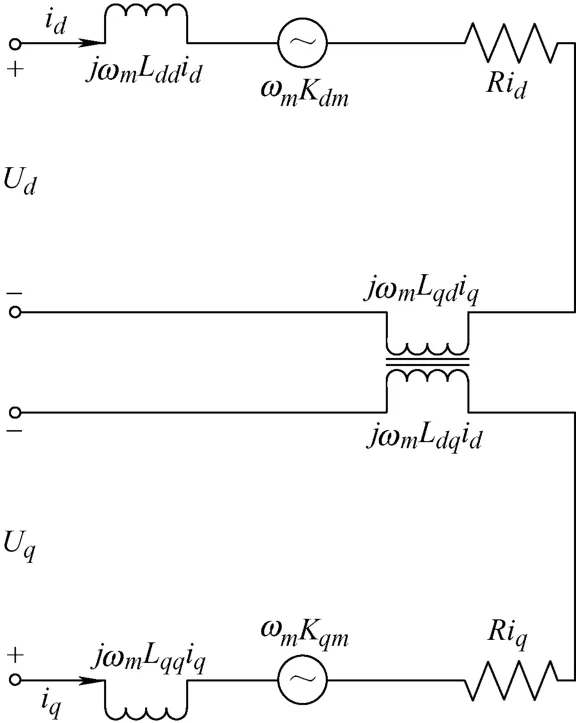
圖1 電壓的數學模型等效電路圖

4 永磁電機的轉矩計算

本節對圖2 所示的12 槽10 極的永磁同步電機的轉矩進行計算。電機采用分數槽集中繞組。 在永磁電機以額定轉速3 000 r/min 運轉的情況下，利用二維有限元模型分析并計算空載反電動勢和定子磁鏈，同時計算電機在不同電流下的轉矩。

圖2 1.5 kW 分數槽永磁同步電機模型

4.1 永磁轉矩及永磁轉矩諧波計算

電機的空載反電動勢如圖3 所示。

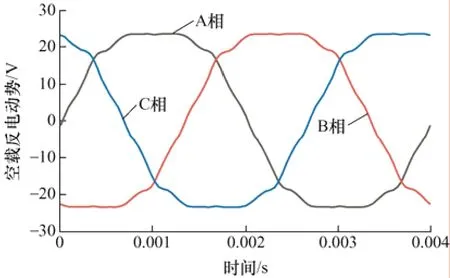
圖3 電機空載反電動勢

利用Park 變換將三相反電動勢轉換為d-q軸上的電壓，由式(10)、(11)計算得到電機的諧波反電動勢常數Kdm和Kqm的幅值如圖4 所示。

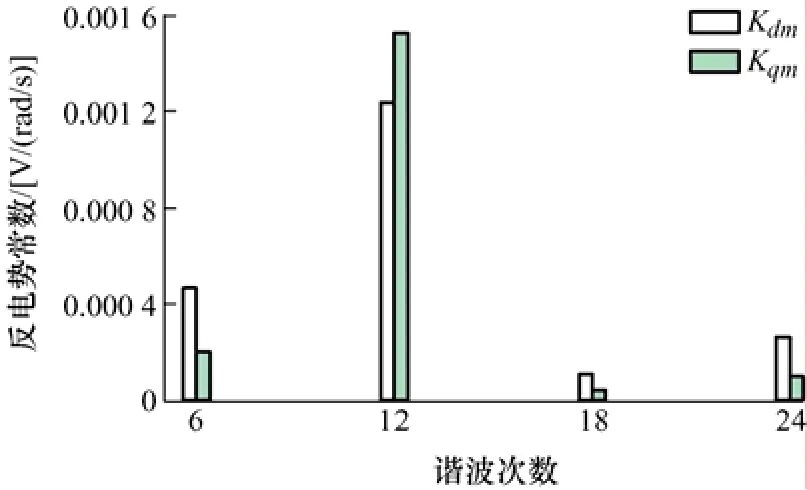
圖4 d-q 坐標系下空載反電動勢常數

其中計算得到的Kdm,0=0.002 9 V/(rad/s)，Kqm,0=0.831 1 V/(rad/s)，然后根據式(7)計算得到不同相電流下的永磁轉矩，如圖5 所示。

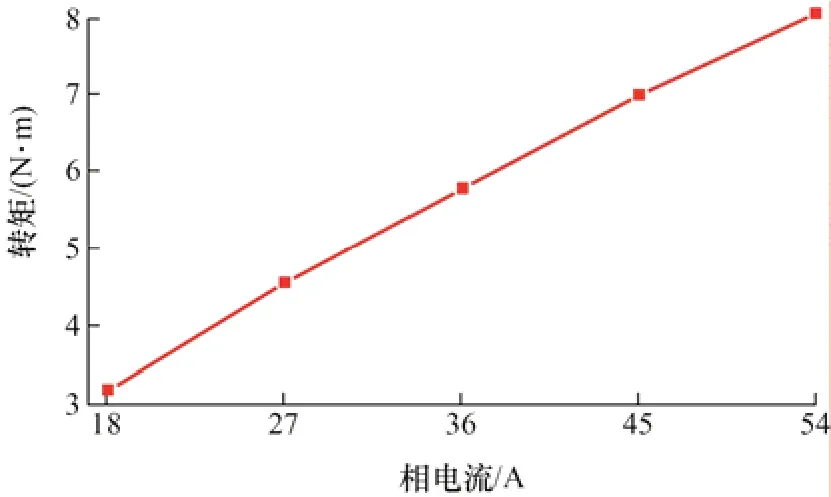
圖5 不同電流下的永磁轉矩

根據計算得到的諧波反電動勢常數幅值，利用式(7)計算出不同相電流下諧波轉矩的幅值，然后根據得到的相位角和式(7)～(9)計算出電機的諧波轉矩，其中給出的d軸和q軸電流與永磁體作用產生的12 次諧波的轉矩如圖6、7 所示。

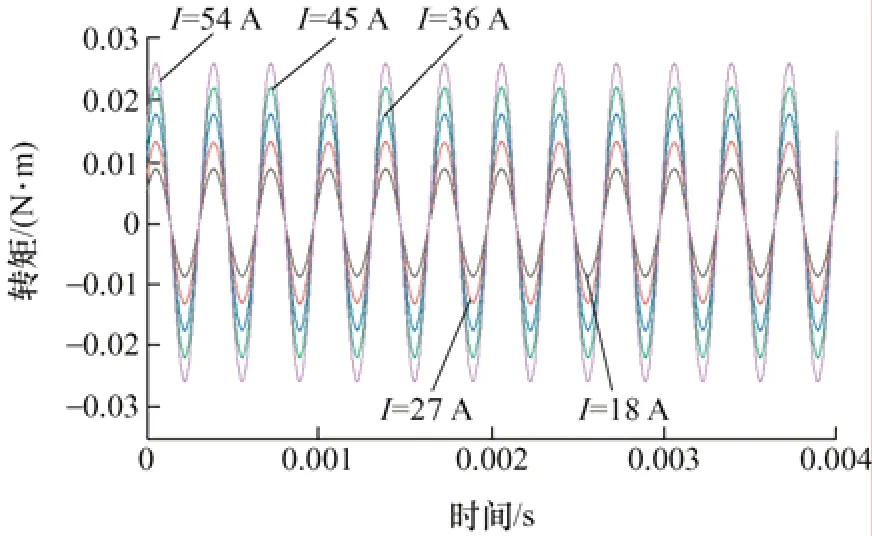
圖6 d 軸電流與永磁體作用產生的12 次諧波轉矩

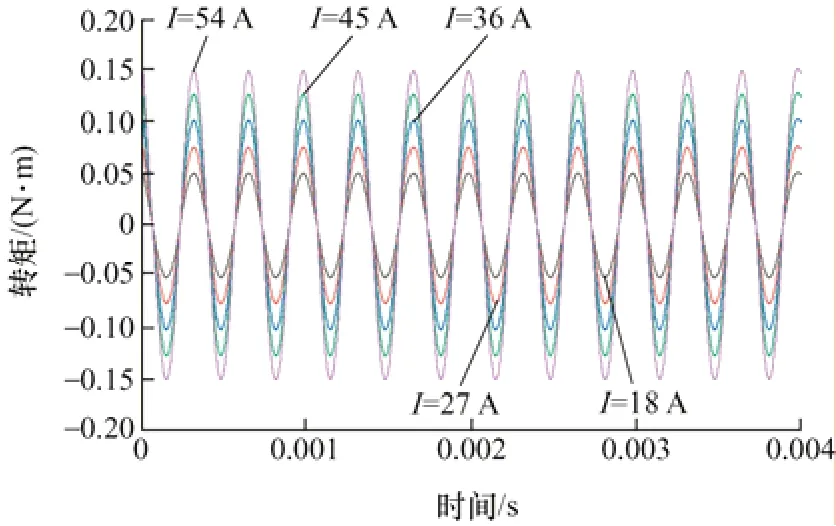
圖7 q 軸電流與永磁體作用產生的12 次諧波轉矩

其中計算得到各電流下的總永磁轉矩脈動如圖8 所示。

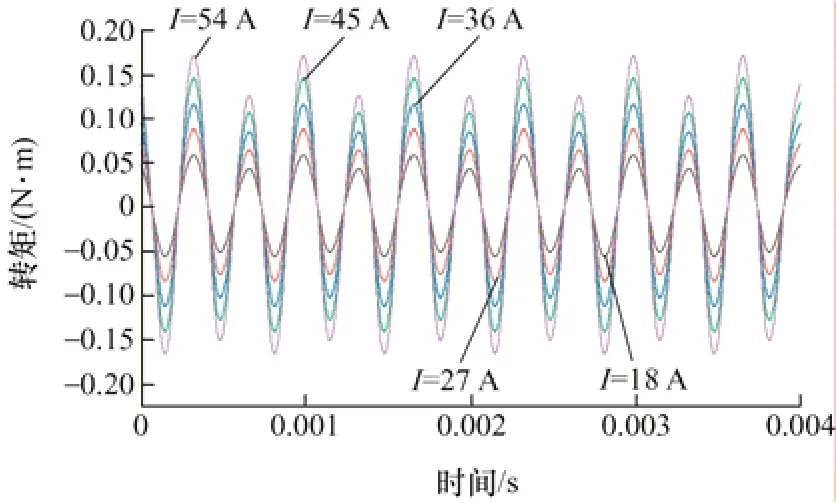
圖8 總永磁轉矩脈動

可以看出，當轉速不變時，反電勢常數不變，此時總永磁脈動轉矩隨著電流的增加而增大。從圖4、7、8 可以看到，12 次諧波反電動勢常數最大，所以永磁轉矩脈動中占比最大的是由q軸電流與永磁體作用而產生的12 次諧波轉矩。

4.2 磁阻轉矩及磁阻轉矩諧波計算

磁阻轉矩計算是將永磁體設置成空氣來凍結磁導率后，對電機施加不同的相電流，電流的有效值分別為18 A、27 A、36 A、45 A、54 A，電流的相位角均為12°。定子只通d軸電流，得到由d軸電流產生的三相磁鏈，利用Park 變換計算得到電機在d軸的自感磁鏈和互感磁鏈，然后進行傅里葉分解得到各個波次的自感磁鏈和互感磁鏈及其相位角，根據式(14)、(15)計算出d軸的自感Ldd和互感Ldq，同樣計算出q軸的自感Lqq和互感Lqd。圖9 給出了當I=54 A 時，凍結磁導率后只加載d軸和q軸電流的磁密云圖。

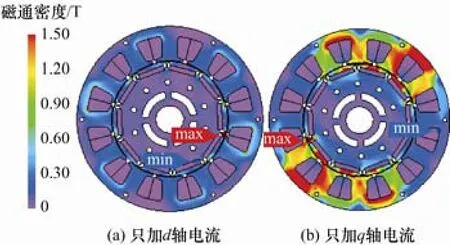
圖9 I=54 A 時電機的磁密云圖

4.2.1 磁阻轉矩計算

圖10 是根據數據和公式計算得到的Lqq,0、Lqd,0、Ldd,0和Ldq,0。圖11 是將Lqq,0、Lqd,0、Ldd,0和Ldq,0代入式(17)計算得到電機在不同電流下的磁阻轉矩。從圖10 中可以看出，隨著電流的增加，電機的q軸自感減小。這是由于電流增大的同時，鐵心飽和程度增加，電機的q軸自感隨之減小。電機的d軸電感隨著電流的增大呈現波動，在36 A達到最大，但整體趨勢是降低的。電機dq軸的互感是相等的，且隨著電流的增大，互感增大，增大趨勢變小。

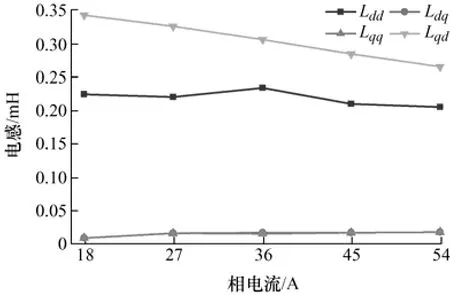
圖10 磁阻轉矩的自感和互感

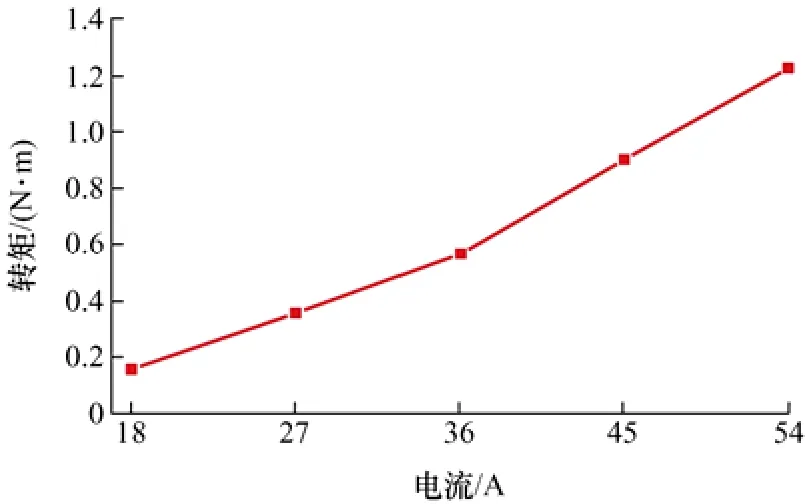
圖11 永磁電機的磁阻轉矩

4.2.2 磁阻轉矩諧波計算

根據得到的數據并利用式(14)、(15)計算出各次諧波的自感和互感，如圖12～15 所示。圖12～15給出了不同電流下各個波次的自感和互感。可以看出，電機在d軸的6 次諧波自感隨著電流增加而增大，12、18 次d軸諧波自感呈現波動，但總體趨勢是增大的，24 次d軸諧波自感電感呈波動總體降低，由此可以得出低次d軸諧波自感隨著電流增加而增大，同時鐵心趨于飽和，使得低次諧波電感增加趨于平緩。6 次、12 次、24 次q軸諧波自感隨著電流增加而降低，18 次q軸諧波自感呈現波動但總體是降低的，所以q軸諧波自感是隨著電流增加而降低。

圖12 6 次諧波的自感和互感

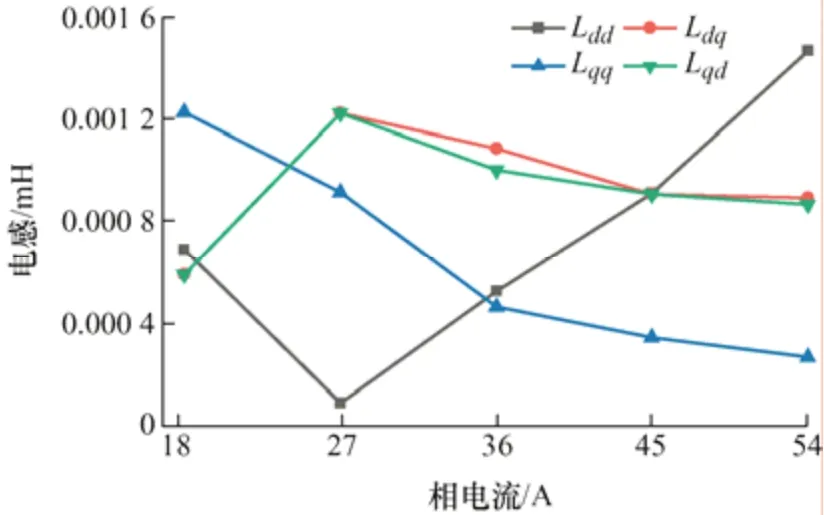
圖13 12 次諧波的自感和互感

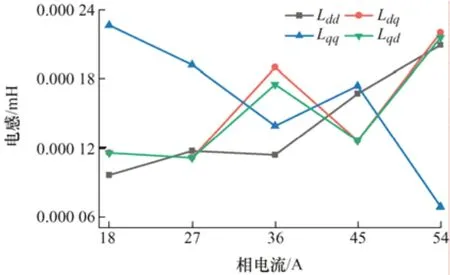
圖14 18 次諧波的自感和互感

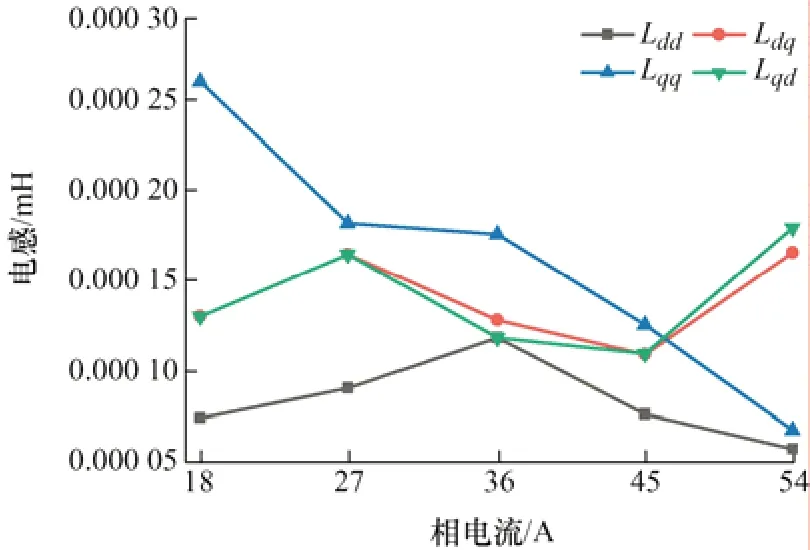
圖15 24 次諧波的自感和互感

當電流I=36 A 時，Ldq不等于Lqd，但是相差很小，近似相等。其他電流下，d-q軸互感Ldq等于Lqd，所以不同電流下，d-q軸互感Ldq等于Lqd，隨著電流的增加，電機的諧波互感呈現不規律的變化。而高次諧波在電流增大時，磁鏈增加趨于平緩，所以高次諧波自感降低。當電流大于27 A 后，6 次和12次諧波互感均大于6 次和12 次q軸自感。

通過計算得到電感和d-q軸電流，并將其代入式(17)計算得到諧波轉矩。其中產生的6 次諧波轉矩Tdd,6、Tdq,6(不計相位角)以及Tqq,6、Tqd,6(不計相位角)如圖16～19 所示。

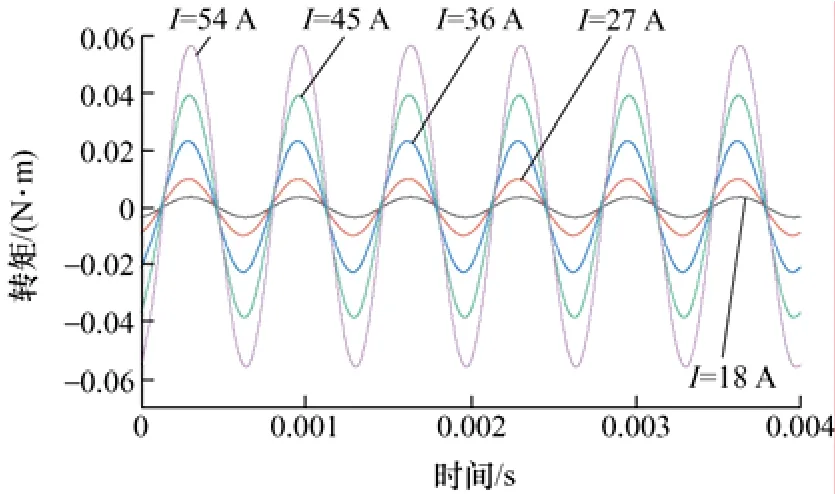
圖16 d 軸電流產生的6 次諧波自感轉矩Tdd,6

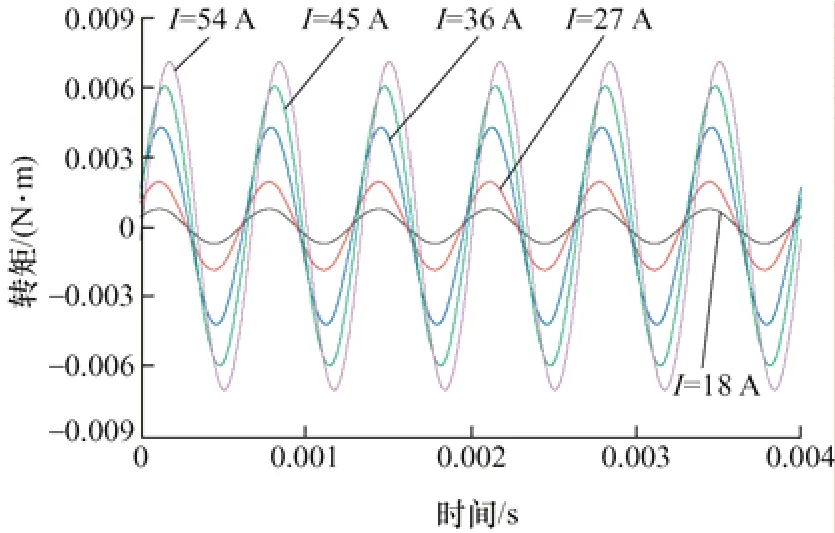
圖17 d 軸電流產生的6 次諧波互感轉矩Tdq,6

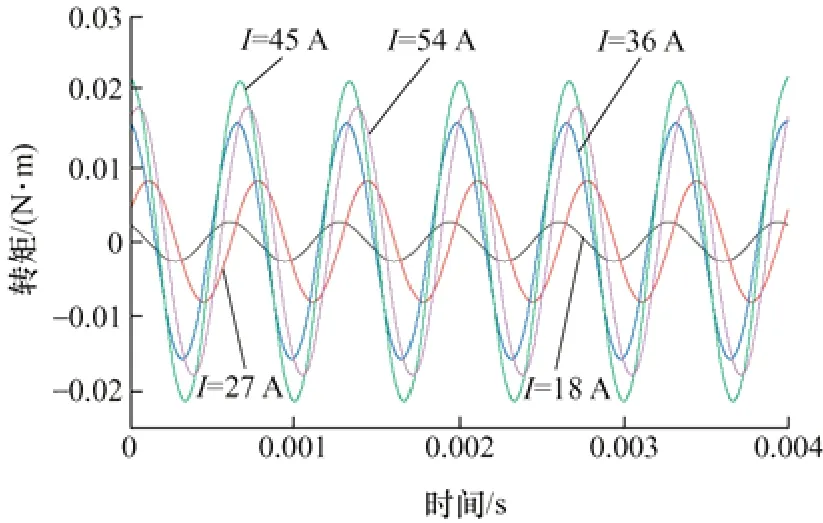
圖18 q 軸電流產生的6 次諧波自感轉矩Tqq,6

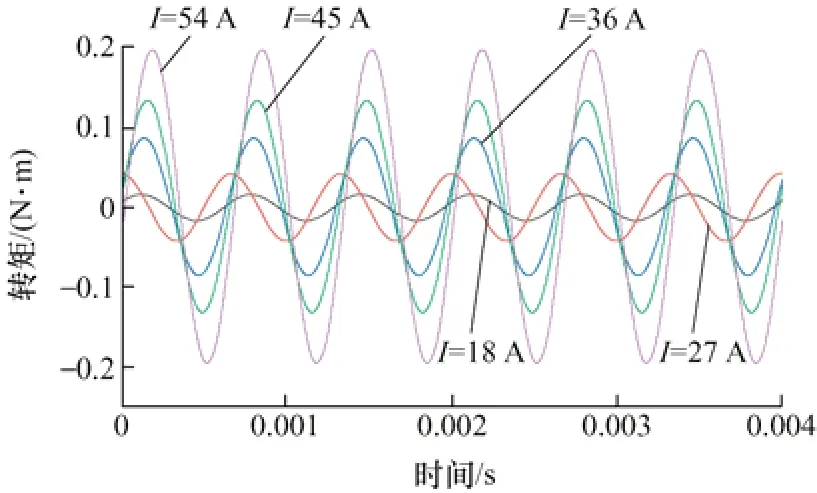
圖19 q 軸電流產生的6 次諧波互感轉矩Tqd,6

從圖16～19 中可以看出，只有相電流等于45 A時的Tqq,6大于相電流等于54 A 時的Tqq,6，其余各個6 次諧波轉矩隨著電流的增加而增大。由于Lqd,6=Ldq,6，q軸電流大于d軸電流，所以Tqd,6大于Tdq,6，且6 次諧波互感轉矩Tqd,6幅值最大，6 次諧波互感轉矩Tdq,6幅值最小。

通過式(21)計算得到不同相電流下的磁阻轉矩總脈動，計算時考慮到不同電感下的相位角，總磁阻脈動轉矩如圖20 所示。

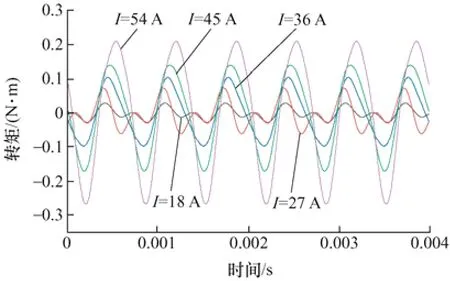
圖20 總磁阻轉矩脈動

圖20 是磁阻轉矩的總脈動，通過計算各個波次的Tqq、Tdd、Tqd和Tdq，然后將各部分相加得到總磁阻轉矩脈動。從圖16～20 可以看出磁阻轉矩脈動中占比最大的是6 次諧波互感轉矩Tqd,6，所以當q軸電流增大時，6 次諧波轉矩增大，總磁阻轉矩脈動也隨之增大。

將上述計算結果相加得到電機在各個電流下的總轉矩如圖21 所示。

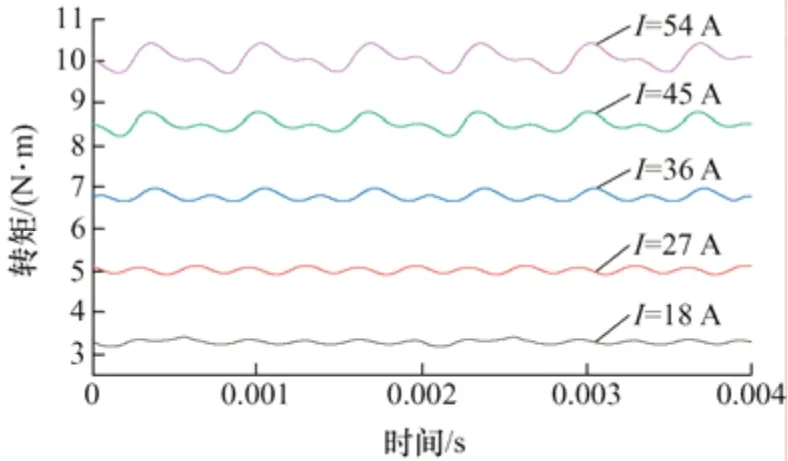
圖21 計算總轉矩

5 仿真驗證

為了驗證分數槽永磁同步電機轉矩計算模型的正確性，利用J-mag 仿真得到不同電流下的轉矩，將其與計算結果對比，如圖22、23 所示。其中圖22 是計算得到的平均轉矩和仿真得到的平均轉矩對比圖，從圖22 中可以看出，計算得到的平均轉矩與仿真得到的完全一致。圖23 對比了不同電流下計算得到的轉矩波形與仿真得到的轉矩波形，從圖23 中可以看出，計算得到的電機轉矩波形和轉矩脈動波形與仿真得到的基本一致。

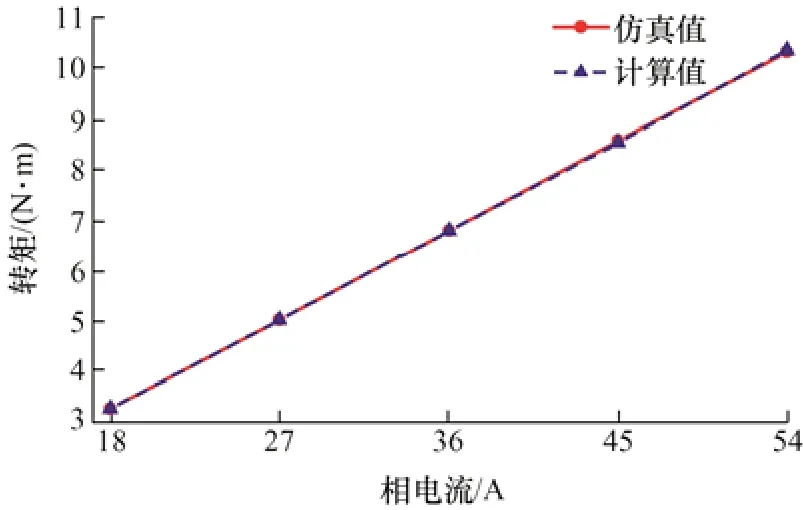
圖22 永磁電機的平均轉矩

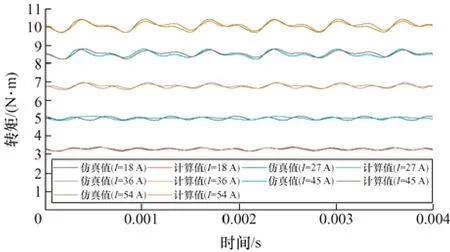
圖23 永磁電機轉矩波形

通過上述結果得到各電流下的轉矩脈動計算結果如表2 所示，計算轉矩脈動值與仿真轉矩脈動值相差最大為0.31%，說明模型計算結果與仿真結果一致。通過上述的結果對比，證明了分數槽永磁同步電機轉矩計算模型是正確的。

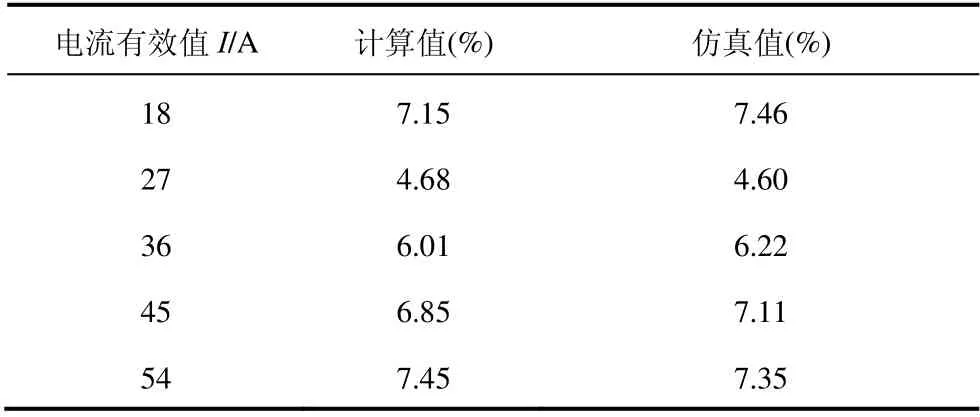
表2 計算轉矩脈動與仿真轉矩脈動對比

6 結論

利用本文提出的分數槽永磁電機轉矩計算模型能夠準確地計算分數槽永磁同步電機的轉矩，并分離出電機的各部分轉矩。

當轉速不變時，反電動勢常數不變，永磁轉矩及諧波永磁轉矩幅值隨相電流呈線性變化，其中對于轉子為“一”字型永磁體的永磁電機，永磁轉矩脈動的主要諧波為q軸電流與轉子磁鏈作用產生的12 次諧波轉矩。

磁阻轉矩與電機在d-q軸下的電感和相電流有關，其中d-q軸下的自感Ldd,0和Lqq,0隨電流的增大而減小，互感Ldq,0等于Lqd,0，隨著電流增加而增大，同時磁阻轉矩隨著電流的增加而增大。磁阻轉矩脈動電機在d-q軸下的諧波電感和定子電流有關，6次諧波d軸自感Ldd,6隨電流增加而增大，當電流大于36 A 后，增加平緩，其他諧波電感隨電流呈不規律變化。其中6 次諧波轉矩Tqd,6為磁阻轉矩脈動的主要諧波。不論是永磁轉矩脈動還是磁阻轉矩脈動，轉矩脈動的主要諧波皆是由q軸電流產生的諧波轉矩。通過計算得到各個電流下電機轉矩的波形與仿真波形一致，驗證了計算模型的正確性。同時，本文的數學模型對計算不同的內置式永磁同步電機的轉矩具有重要意義。