理法交融打通計算快速航道
——以“四舍五入法試商、調商”的高階思維教學為例

江蘇省南京市南師附中樹人學校附屬小學 林紅梅

數學課程標準指出：“運算能力主要是指能夠根據法則和運算律正確地進行運算的能力。”這一敘述強調了兩點：一是培養運算能力要注意引導學生“理解算理，自主發現算法”，二是要注意與通常理解的運算技能概念的區別。

一、借助情境，引導學生理解運算方法中的“微”

孫曉天認為，運算方法是指基于算理，能“合理、簡捷”進行的運算途徑。教師可引導學生運用學習過的知識遷移解決新出現的問題。如教學“除法運算”時，當除數不是整十數的時候，我們可以把這個數看成接近的整十數。

細節回放：

（一）四舍法試商

師（出示例題）：這本書有96頁，小云每天看32頁，幾天可以看完？

師：你們會列式嗎？

生：96÷32。

（板書：96÷32）

師：你能先估一估嗎？

生：結果是3。

師：結果是3，我們是估出來的，我們能不能算一算，看我們估的對不對呢？

師：這個跟我們之前學的計算一樣嗎？哪里不一樣？你有什么好辦法？

生1：不一樣，之前學得除數都是整十數。

生2：我們可以把除數32看成整十數30。

師：為什么看成30？

生：因為32最接近30。（強調：最接近）

師：如果是31，可以看成多少？33、34呢？

生：都可以看成30。

師：像這樣，個位上是1、2、3、4的兩位數，我們可以用四舍法把個位上的數舍去，看成整十數。

師：商寫在哪一位上，為什么？

生1：商寫在個位上，因為96里最多有3個30。

生2：小云每天看32頁，96頁里面有3個32 ，所以商寫在個位上，和6對齊。

（板書：3個32）

師：下面3和誰相乘？

生1：3和32相乘，因為小云每天看的頁數是32頁，不是30頁。

生2（指著板書中的豎式）：原來的除數是32，為了便于試商，我們把32看成其最接近的整十數30，所以商3應該和原來的除數32相乘。

出示豎式（如圖1）：

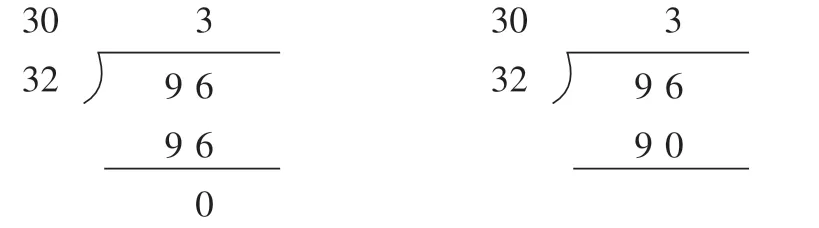
圖1

（二）五入法試商

師（出示例題）：這本書有192頁，小明每天看39頁，幾天可以看完？嘗試先估后算。

師：39可以看成多少？為什么？那36、37、38呢？

生：都可以看成40，因為這些數最接近40。

師：你們真聰明呀，像這樣個位上是6、7、8、9的兩位數我們可以用五入法把它看成整十數。

師：請同學們回顧這兩道題，當除數不是整十數時怎么辦？計算過程中還要注意什么？

先估算，再筆算，最后結合情境理解算理，做到理法融合，引導學生掌握科學的算法，在優化算法的學程中，進一步夯實算理內化于心的基礎。由此探求算理與算法有機結合，有利于提高學生“以深度思維為核心”的計算能力與計算正確率。

在教學“四舍五入法試商”這一課時，教師注重對“96÷32=”這道算式運算方法的講解，結合具體的情境，講清楚怎樣進行試商，當選擇四舍法試商的時候，教師引導學生借助情境講清試商后的計算過程：要用商（3）乘原來的除數（32），而不能用3乘30，因為每天看的是32頁，而不是30頁，如果用3乘30的話，這本書才90頁，不符合情境中的“這本書有96頁”這一條件。接著，教師繼續引導學生進行新方法的嘗試“192÷39=”，學生有了“四舍”的經驗，很容易聯想到“五入”的方法。如此細致入微的引導，學生自然能夠理解四舍五入法試商的運算方法。

二、借助生成，引導學生掌握運算原理中的“微”

算法和算理是運算能力的一體兩翼，兩者相輔相成。孫曉天認為，算理是指關于什么是運算及如何運算的道理，大體上可分為三個遞進的層次，即什么是運算、運算的總體規則及具體的運算規則。在數學課堂上引導學生進行思維碰撞，用問題來驅動學生的求知欲望，用多個事例進行對比，尋找問題根源，從而讓學生明白解決問題的道理。

細節回放：

師（出示例題）：四年級（1）班有34人，一共借書272本。四年級（1）班平均每人借書多少本？

師：算式怎么列？

生：272÷34。

（板書：272÷34）

師：你能估一估每人借到幾本嗎？

生：8本或9本。

師：到底商是多少呢？

生1：8本。

生2：9本。

師：在豎式計算過程中，你發現了什么問題？在豎式上圈一圈。

展示學生作品（如圖2）：

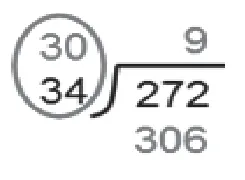
圖2

生：如果每人借9本，34人要借306本，超過272本，說明初商可能偏大。

師：初商偏大，到底什么原因呢？再次觀察豎式（圈出除數34和30）

生：除數變小，因為把34看作30，用30來估商，得到初商9，但是真正乘的時候是原來的除數34×9=306，所以偏大。

師：我們再來看看類似的豎式。仔細觀察這4道列好的豎式，他們的初商怎么樣了？

出示豎式（如圖3）：

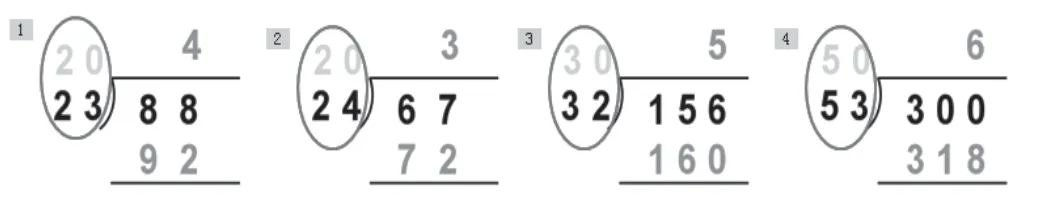
圖3

生：初商偏大了。

師：是什么原因造成的？

生：圈出除數，發現都是用四舍法試商，除數變小了。

在教學“四舍法調商”這一課時，教師注重對“272÷34”這道算式的運算原理進行指導，重點引導學生圍繞四舍法試商后，初商會偏大的問題進行思考，借助學生生成“因為把除數34看成了30，除數看小了，所以才會出現初商偏大”的結論，再次借助情境“一班有34人”，不是30人，所以用初商9乘34之后會超過272本，要想解決這一問題，就需要把初商9調小1變成8，再次計算得出正確結果。這一例題完成之后，教師沒有停止教學，繼續出示了一組題目，引導學生進一步體會“除數看小，初商偏大，需要調小”這一道理。

三、借助習題，引導學生運用運算思維中的“微”

從學科關鍵能力的含義來看，運算能力涵蓋著抽象、推理、建模等基本的數學思想。運算能力的形成對小學生的整體數學能力的培養與提升起到了基石的作用。進一步分析運算能力，繼續發掘運算能力背后的思維，我們又可以發現智慧技能在其中的發展。由此，運算能力不單純是計算技能，還是在運算能力形成、發展過程中，學生思維和數學素養的整體體現。《義務教育數學課程標準（2011年版）》的課程內容安排及蘇教版數學教材的編排體系，對運算能力評價采用分段評價及綜合評價兩種方式。對運算能力評價內容的選取，折射出對運算能力含義的正確理解。因此，運算能力的練習內容絕不能只選取單一的計算式題，而是要選取能反映出學生對算理的理解、算法的選擇與創新、運算策略的運用等綜合能力的內容。深度學習和高階思維要出現評價題， 在教學“四舍法調商”這一課時，新課內容教學完畢之后，為了進一步深化“四舍法調商”知識，教師出示了一道練習題（如圖4），進行了兩次調商得到結果。

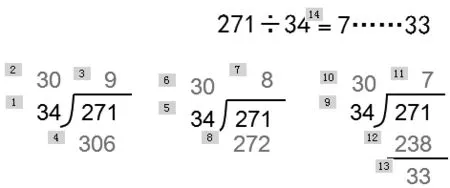
圖4

正因師生關系的實質轉變，提高了融合算理算法教學的實效性。在計算教學中放緩腳步，著力“理法相融，思維高階”，讓學生“慢探究”“慢建構”“慢思考”，通過“慢教學”，使學困生充分經歷數學活動，掌握數學結構，品味數學思想，點燃高階思維火花，從而提高他們的計算能力。當今數學課堂，對數學教師的角色期待與素養要求提出了高標準，由主宰者到引領者、告訴者到讓學者、照搬者到研究者、享用者到研究者等，多重角色新定位。

在“四舍法調商”這一課上，當遇到初商偏大時進行一次調商，之后仍然偏大，這時候學生們的思維產生碰撞，順著課堂的內容繼續思考下去，在第二次調商后，尋找到了正確的答案。學生經歷了兩次調商的矛盾沖突，自然引發了學生的深度思考，真正做到了理法相融。