Scratch插入排序算法

陳新龍

排序算法是編程考試中最常見的題目，幾乎所有的筆試和面試都會考到，因為它體現的就是程序員的算法基礎和邏輯思維能力，經常看《電腦報》的讀者們都知道，我們已經講了多種排序算法比如冒泡排序、選擇排序、桶排序……

那么大家有沒有思考一個問題：為什么有那么多種的排序算法呢？首先是因為排序的思路是具有多樣性的，從不同的角度解決排序問題，就會產生不同的排序方法。另外，不同的排序算法各有優勢和劣勢，當數據規模不同時，可以選擇合適的排序算法。

今天就和大家分享一個新的排序算法“插入排序”，插入排序分為前插序和后插序，它的基本思想是將數組的第一個數認為是有序數組，從后往前或者從前往后掃描該有序數組，把數組中剩余n-1個數，根據數值大小，有序插入到前面序列中，直至數組所有數有序排列為止。這樣的話，n個元素只需要進行n-1趟排序，比多數排序算法的效率更高。

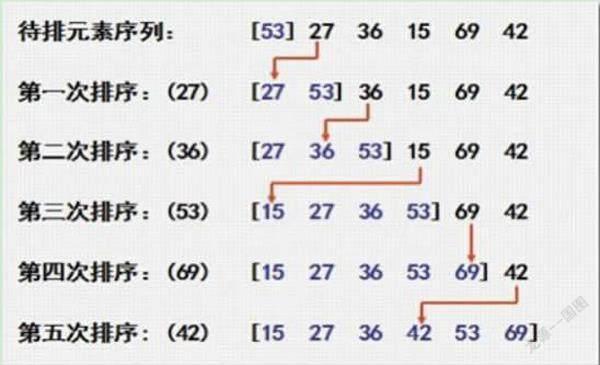
例如有一組數列為【53、27、36、15、69、42】。首先對于待排序數組中第一個元素53認定為有序元素，所以排序從第二個元素27開始。第一次排序時從有序數列中查找27插入的位置。27小于53應插入在53之前，此時將27提取出來后，將53后移，將27放入原53點位置，便完成了第一次排序。

第二次排序的時候從有序序列中找36的插入位置。36小于53，大于27，36的插入位置在27與53之間。此時將36提取出來后，將53后移，再將36放入原53所在位置，便完成了第二次的排序。

剩余的數字15、69、42的排序過程相同，找到合適的位置通過移動、插入的方法完成排序。最終的排序數列結果為【15、27、36、42、53、69】總計五次排序。

了解了插入排序的運行過程和思路后，我們可以嘗試著用Scratch將代碼拼搭出來。首先新建兩個列表用于存放原始數列和排序后的數列，開始時將序列中所有的內容全部清空。通過重復執行的方法，將1-50之間的隨機數添加入原數列列表中（隨機數的范圍和重復執行的次數可自定義）。

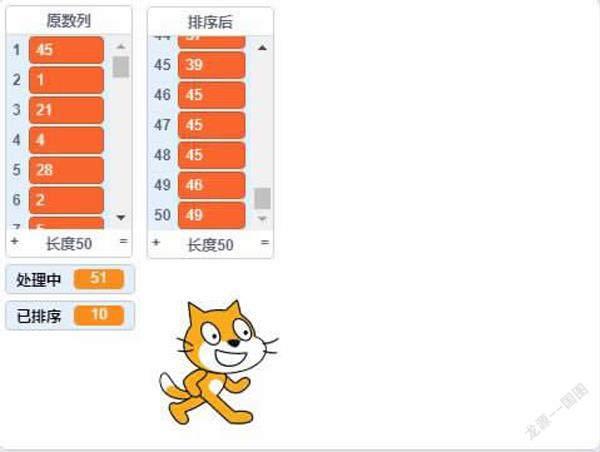
其次新建 “處理中”和“已排序”兩個關鍵變量。由于插入排序是從第二項開始，所以變量“處理中”表示需要插入排序的數列的序列位置。變量“已排序”代表數列中已經完成排序的數列組從第一項開始的，一直重復執行直到處理中的項數大于數列項數的總和便可跳出循環。在循環中，將需要處理的數和已排序數列中的數字進行比較大小，通過比較大小將處理中的數字插入到合適的位置。處理中的數排在已排序數列的下一個數字，同時處理中的數字跟隨著循環每次加一，直至循環數列末尾，排序結束。

插入排序的優點就是穩定，速度快，但是比較次數不一定，比較次數越少，插入點后的數據移動越多，特別是當數據總量龐大的時候，需要用鏈表解決這個問題。