非相關(guān)源與相干源并存的信源數(shù)估計(jì)

余小玲，龔曉峰，雒瑞森

(四川大學(xué)電氣工程學(xué)院，四川 成都 610065)

1 引言

空間譜陣列信號(hào)處理在雷達(dá)、通訊、導(dǎo)航和電子對(duì)抗領(lǐng)域有著廣泛的應(yīng)用前景。基于特征子空間的高分辨譜估計(jì)技術(shù)中大部分算法要求信源個(gè)數(shù)精確已知。當(dāng)估計(jì)的信號(hào)源數(shù)目與真實(shí)的信號(hào)源數(shù)目不一致時(shí)，空間譜曲線中的峰值個(gè)數(shù)與實(shí)際源數(shù)不相同，會(huì)對(duì)真實(shí)信號(hào)的估計(jì)產(chǎn)生嚴(yán)重的影響。然而，在實(shí)際應(yīng)用場(chǎng)合，信號(hào)源數(shù)往往是一個(gè)未知數(shù)。所以，信源數(shù)的準(zhǔn)確估計(jì)是子空間類譜估計(jì)算法需要解決的關(guān)鍵問(wèn)題。

針對(duì)信源數(shù)估計(jì)問(wèn)題，相關(guān)學(xué)者提出了很多較為有效的方法，包括Akaike 信息論(AIC)準(zhǔn)則[1]、最小描述長(zhǎng)度(MDL)準(zhǔn)則[2]、有效檢測(cè)(EDC)準(zhǔn)則、蓋氏圓法(GDE)[3]以及正則相關(guān)技術(shù)(CCT)[4]。這些算法能準(zhǔn)確估計(jì)信號(hào)源不相關(guān)或者獨(dú)立時(shí)的個(gè)數(shù)，但是在多徑傳播和復(fù)雜電磁干擾背景下，會(huì)產(chǎn)生大量的強(qiáng)相關(guān)或相干信號(hào)，信號(hào)子空間會(huì)向噪聲子空間擴(kuò)散，造成秩虧，導(dǎo)致算法失效[5]。因此相干信源估計(jì)問(wèn)題，首先應(yīng)是對(duì)信號(hào)解相干。圍繞信號(hào)的解相干問(wèn)題，很多有效算法被提出，大致分為兩類：一類是空間平滑類；另一類是矩陣重構(gòu)類。空間平滑類算法的原理是將空間平滑算法與信息論的方法相結(jié)合來(lái)實(shí)現(xiàn)相干信源數(shù)目的估計(jì)。主要包括前向空間平滑算法[6]、前后向空間平滑算法[7]以及空間差分平滑算法[8]。該算法是是通過(guò)犧牲有效陣元數(shù)目、實(shí)現(xiàn)解相干，會(huì)造成陣列孔徑的損失。矩陣重構(gòu)法的原理是直接利用陣列接收快拍數(shù)據(jù)或利用數(shù)據(jù)協(xié)方差矩陣進(jìn)行矩陣重構(gòu)方式解相干。主要包括矩陣分解法[9]和Toeplitz法[10-12]。該算法在低信噪比時(shí)性能良好，得到廣泛應(yīng)用。

本文針對(duì)非相關(guān)源與相干源共存時(shí)的信源數(shù)目估計(jì)問(wèn)題，利用陣元接收信號(hào)間的互相關(guān)信息，構(gòu)造一個(gè)秩只與相干源信息有關(guān)的差分矩陣，從而將非相關(guān)源與相干信源的估計(jì)分辨開(kāi)。該算法首先利用SORTE法估計(jì)相互獨(dú)立信源個(gè)數(shù)，結(jié)合非相關(guān)信源導(dǎo)向矢量、相干信源陣列導(dǎo)向矢量矩陣分布與噪聲子空間正交特性的差異，根據(jù)DOA估計(jì)結(jié)果得到非相關(guān)信源數(shù)估計(jì)。然后通過(guò)利用陣元接收信號(hào)間的相互關(guān)系，構(gòu)造差分矩陣，最后利用SORTE法實(shí)現(xiàn)相干信源數(shù)估計(jì)。

相比常規(guī)信源數(shù)估計(jì)算法，本算法將非相關(guān)信源與相干信源分開(kāi)分辨，重復(fù)利用陣列接收數(shù)據(jù)，具有更強(qiáng)的信源承載能力及陣元節(jié)省能力，且精確度較高。

2 信號(hào)接收模型

信號(hào)接收陣列模型如圖1所示。

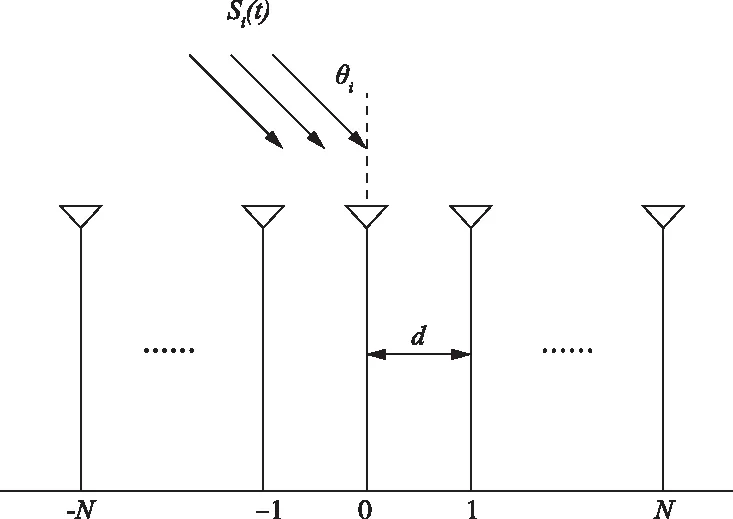
圖1 信號(hào)接收陣列模型

假設(shè)有M個(gè)窄帶遠(yuǎn)場(chǎng)信號(hào)源Si(t)以角度θi(i=1，2，…，M)入射到空間陣列上，其中陣列天線由2N+1個(gè)線性分布陣元組成，假設(shè)陣列中各陣元是各向同性的且不存在通道不一致、互耦等因素的影響，如圖1所示。假設(shè)噪聲為零均值、方差為δ2的高斯白噪聲，陣元間噪聲彼此獨(dú)立，且與信號(hào)不相關(guān)。以中間陣元為參考陣元，則其陣列接收信號(hào)寫(xiě)成矢量表達(dá)式為

X(t)=A(θ)S(t)+V(t)

(1)

式中，X(t)為陣列接收的快拍數(shù)據(jù)的矢量表達(dá)式；A(θ)為對(duì)應(yīng)的(2N+1)×M階陣列流形矩陣；V(t)為噪聲矢量，R為信號(hào)協(xié)方差矩陣。

X(t)=[x-N(t)，…，x-1(t)，x0(t)，x1(t)，…，xN(t)]T

(2)

A(θ)=[a(θ1)，a(θ2)，…，a(θM)]

(3)

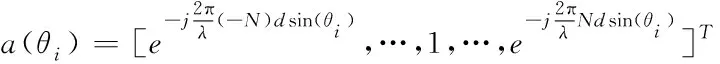
(4)

S(t)=[s1(t)，s2(t)，…，sM(t)]T

(5)

V(t)=[v-N(t)，…，v-1(t)，v0(t)，v1(t)，…，vN(t)]T

(6)

R=E[X(t)XH(t)]

(7)

3 算法原理

3.1 非相關(guān)信源數(shù)估計(jì)

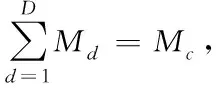
(8)

SORTE信源估計(jì)法主要思想是利用特征值二階統(tǒng)計(jì)方差信息構(gòu)造信源估計(jì)判決函數(shù)[13]。

若定義M1=Mu+D、?λi=λi-λi+1，其中i=1，…，2N，則有

?λM1+1=?λM1+2=…=?λ2N=0

(9)

定義特征值的方差為δk。

(10)

其中，k=1，…，2N。

定義SORTE函數(shù)為

(11)

由式(11)得，SORTE函數(shù)滿足如下關(guān)系：

(12)

則獨(dú)立信號(hào)(非相關(guān)信號(hào)與相干信號(hào)組之和)源估計(jì)的判決函數(shù)為

1

(13)

結(jié)合，非相關(guān)信源導(dǎo)向矢量、相干信源陣列導(dǎo)向矢量矩陣分布與噪聲子空間正交特性的差異，根據(jù)DOA估計(jì)結(jié)果得到非相關(guān)信源數(shù)估計(jì)。

3.2 相干信源數(shù)估計(jì)

假設(shè)M個(gè)信號(hào)中前L個(gè)相干，其余各信號(hào)間不相關(guān)，則第n個(gè)陣元上的接收信號(hào)為

(14)

式中，n=-N，…，-1，0，1，…，N;βi=ρiejΔφi，ρi>0，i=1，2，…，L;Φ=-2πd/λ。定義第n個(gè)和第k(k≥0)個(gè)陣元上接收信號(hào)的互相關(guān)為

(15)

同理，對(duì)應(yīng)的第-k(-k≤0) 個(gè)與第-n個(gè)陣元上的接收信號(hào)的互相關(guān)為

(16)

用第k個(gè)陣元與所有陣元的接收信號(hào)的互相關(guān)構(gòu)造如下(N+1)×(N+1)維Toeplitz矩陣

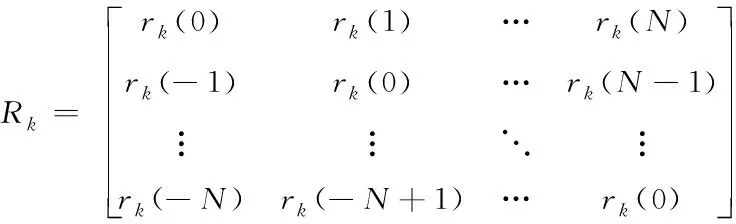
(17)

同理用對(duì)應(yīng)第-k個(gè)陣元與所有陣元的接收信號(hào)的互相關(guān)，構(gòu)造如下(N+1)×(N+1)維Toeplitz矩陣

(18)

構(gòu)造差分矩陣

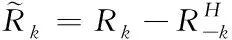
(19)

為了提高協(xié)方差矩陣特征空間對(duì)噪聲擾動(dòng)的魯棒性，所有陣列的互相關(guān)性和自相關(guān)性都被采用，按如下處理所有的差分矩陣

(20)

文獻(xiàn)[14]已證明，通過(guò)構(gòu)造差分矩陣達(dá)到了相干信源去相干的目的。

對(duì)于入射信源中有多個(gè)相干信源組的混合情況，由單組相干信源同理可推導(dǎo)。

3.3 算法的基本步驟

綜上所述，本文算法基本步驟如下：

1)利用SORTE得到非相關(guān)信源數(shù)和相關(guān)信源組數(shù)。

2)結(jié)合常規(guī)分辨方法中非相關(guān)信源陣列導(dǎo)向矢量與噪聲子空間正交關(guān)系特性，得到非相關(guān)信源數(shù)目的估計(jì)。

3)構(gòu)造差分矩陣。

4)對(duì)差分矩陣分解得到的特征值，利用SORTE算法估計(jì)得到相干信源數(shù)。

4 數(shù)值仿真與分析

為驗(yàn)證本文算法的性能，將本文算法與基于FSS、FBSS、SDS和Toeplitz矩陣重構(gòu)的解相干算法進(jìn)行比較。同時(shí)，為了驗(yàn)證算法的有效性，進(jìn)行了4組仿真。

實(shí)驗(yàn)一：?jiǎn)谓M相干源時(shí)驗(yàn)證算法解相干能力對(duì)信噪比和快拍數(shù)的敏感程度，考慮均勻線陣的陣元數(shù)為13，陣元間距為半波長(zhǎng)。其中2個(gè)非相關(guān)信號(hào)和一組4個(gè)相干窄帶信號(hào)同時(shí)入射到陣列上，非相關(guān)信號(hào)DOA分別為[20°，30°]，一組相干信號(hào)DOA分別為[-20°，10°，-50°，0°]。假設(shè)噪聲為零均值、方差為δ2的高斯白噪聲，陣元間噪聲彼此獨(dú)立，且與信號(hào)不相關(guān)。Monte Carlo實(shí)驗(yàn)次數(shù)為100。圖2是采樣快拍數(shù)為200時(shí)成功檢測(cè)概率與SNR關(guān)系曲線，圖3是SNR為15dB時(shí)成功檢測(cè)概率與快拍數(shù)的關(guān)系曲線。

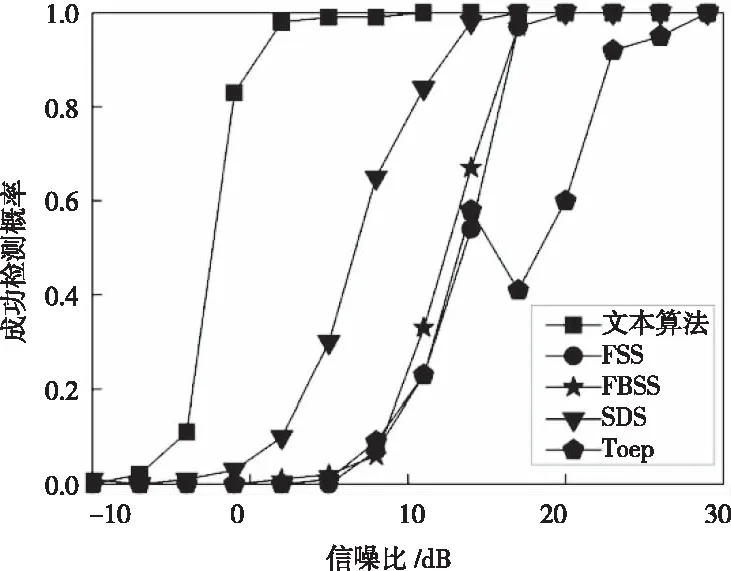
圖2 單組相干源時(shí)算法對(duì)信噪比的敏感程度

圖3 單組相干源時(shí)算法對(duì)快拍數(shù)的敏感程度

如圖2所示，本文算法在低信噪比下性能明顯高于另外4種算法，并且在信噪比為-10dB～30dB，步進(jìn)為3dB下，信噪比為2dB時(shí)，成功檢測(cè)概率達(dá)到98%以上，由此可見(jiàn)本文算法對(duì)信噪比的敏感度較低。

如圖3所示，即使在快拍數(shù)很小的情況下，本文算法依舊可以保證99%以上的正確率，即快拍數(shù)對(duì)最后的估計(jì)結(jié)果幾乎不會(huì)造成影響，取信噪比為15dB快拍數(shù)為20到200，步進(jìn)為20。SDS 算法在快拍數(shù)為200時(shí)正確率才能達(dá)到 96%，另外3種算法，即使在快拍數(shù)達(dá)到200的情況下正確率也沒(méi)有達(dá)到80%。

實(shí)驗(yàn)二：多組相干源時(shí)驗(yàn)證算法解相干能力對(duì)信噪比和快拍數(shù)的敏感程度。其中2個(gè)非相關(guān)信號(hào)和兩組4個(gè)相干信號(hào)同時(shí)入射到陣列上，非相關(guān)信號(hào)DOA分別為[20°，30°]，第一組相干信號(hào)DOA分別為[-20°，10°]第二組相干信號(hào)DOA分別為[-40°，0°]。其它仿真參數(shù)同實(shí)驗(yàn)一。圖4是采樣快拍數(shù)為200時(shí)成功檢測(cè)概率與SNR關(guān)系曲線。圖5是SNR為15dB時(shí)檢測(cè)概率與快拍數(shù)的關(guān)系曲線。

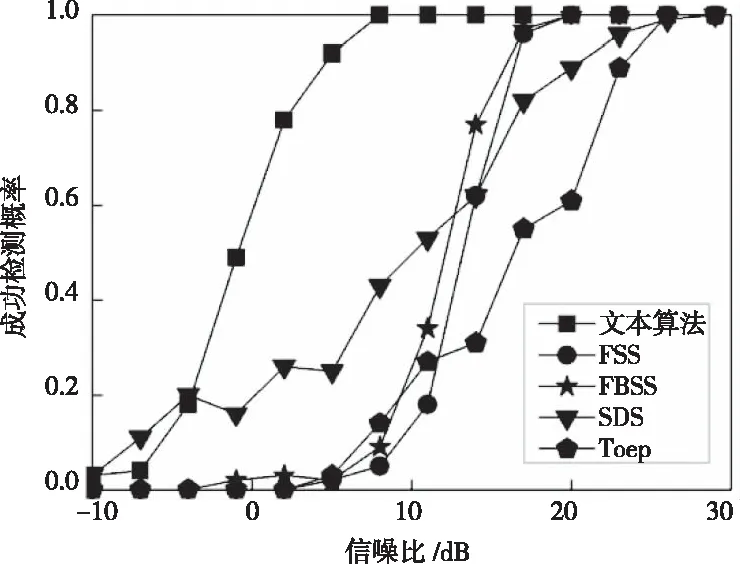
圖4 兩組相干源時(shí)算法對(duì)信噪比的敏感程度

圖5 兩組相干源時(shí)算法對(duì)快拍數(shù)的敏感程度

如圖4所示當(dāng)信噪比大于26dB時(shí)5種算法的正確率均可以達(dá)到100%，但是在信噪比的敏感程度上，本文算法最優(yōu)，在5dB時(shí)的正確率就可以達(dá)到100 %。

如圖5所示，在快拍數(shù)為40的情況下本文的正確率就可以達(dá)到100%，其它4種算法，即使在快拍數(shù)達(dá)到200時(shí)，正確率也均低于90%。

實(shí)驗(yàn)三：?jiǎn)谓M相干源角度接近時(shí)驗(yàn)證算法解相干能力對(duì)信噪比和快拍數(shù)的敏感程度。其中2個(gè)非相關(guān)信號(hào)和一組4個(gè)相干信號(hào)同時(shí)入射到陣列上，非相關(guān)信號(hào)DOA分別為[7°，-21°]，相干信號(hào)DOA分別為[-20°，5°，-30°，0°]，其它仿真參數(shù)同實(shí)驗(yàn)一。圖6是采樣快拍數(shù)為200時(shí)成功檢測(cè)概率與SNR關(guān)系曲線。圖7是SNR為15dB時(shí)成功檢測(cè)概率與快拍數(shù)的關(guān)系曲線。

圖6 相干源角度接近時(shí)算法對(duì)信噪比的敏感程度

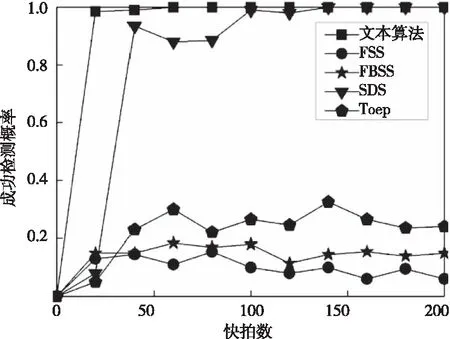
圖7 相干源角度接近時(shí)算法對(duì)快拍數(shù)的敏感程度

如圖6、圖7所示，當(dāng)非相關(guān)信源與相干信源角度接近時(shí)傳統(tǒng)的FSS、FBSS和Teop算法通過(guò)空間平滑或矩陣重構(gòu)之后仍可能是秩虧的狀態(tài)，因此正確率較低，但是本文算法和SDS是通過(guò)差分構(gòu)造差分矩陣將非相關(guān)源和相干源區(qū)分開(kāi)，因此分辨率不受角度間隔的影響。

實(shí)驗(yàn)四：信源數(shù)等于陣元數(shù)時(shí)驗(yàn)證算法解相干能力對(duì)信噪比和快拍數(shù)的敏感程度。其中9個(gè)非相關(guān)信號(hào)和一組4個(gè)相干信號(hào)同時(shí)入射到陣列上，非相關(guān)信號(hào)DOA分別為[20°，30°，-10°， -45°，40°，-60°，60°，15°，-25°]，一組相干信號(hào)DOA分別為[-20°，10°，-50°，0°]。其它仿真參數(shù)同實(shí)驗(yàn)一。圖8是采樣快拍數(shù)為200時(shí)成功檢測(cè)概率與SNR關(guān)系曲線。圖9是SNR為15dB時(shí)成功檢測(cè)概率與快拍數(shù)的關(guān)系曲線。

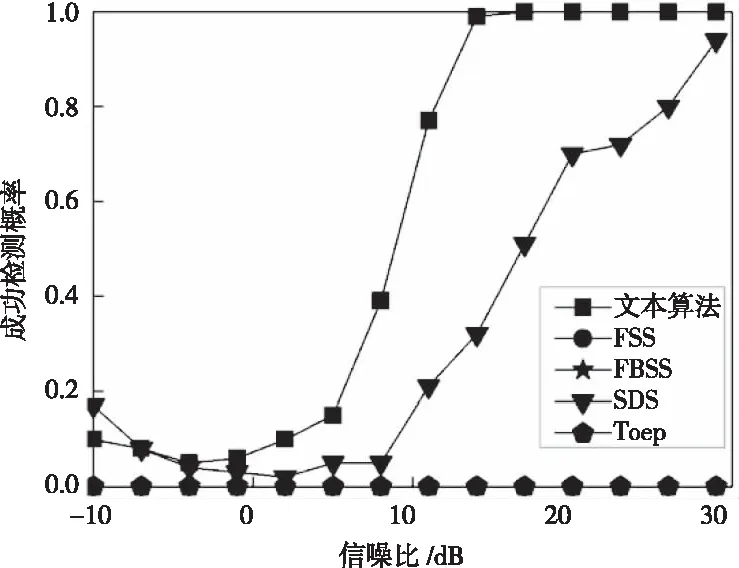
圖8 信源數(shù)等于陣元數(shù)時(shí)算法對(duì)信噪比的敏感程度

圖9 信源數(shù)等于陣元數(shù)時(shí)算法對(duì)快拍數(shù)的敏感程度

如圖8、圖9所示，當(dāng)入射信源數(shù)等于陣列元數(shù)時(shí)，F(xiàn)SS、FBSS、Toep算法均失效，只有本文算法和SDS能夠檢測(cè)13個(gè)信號(hào)，顯然本文算法的精確度較SDS高，且在信噪比為11dB時(shí)，正確率達(dá)到99%，對(duì)快拍數(shù)的敏感程度顯然也優(yōu)于SDS。在信源數(shù)等于陣元數(shù)時(shí)仍有較好的估計(jì)結(jié)果，可見(jiàn)本文的算法的信源承載能力較強(qiáng)。

5 結(jié)束語(yǔ)

針對(duì)相干源與非相關(guān)源并存時(shí)的信源數(shù)目估計(jì)問(wèn)題，提出了一種基于差分算法的信源數(shù)估計(jì)方法。利用陣元間的互相關(guān)信息構(gòu)造差分矩陣，使其秩只與相干源的信息有關(guān)，達(dá)到相干源解相干。該算法首先利用SORTE法估計(jì)獨(dú)立信源的個(gè)數(shù)，結(jié)合常規(guī)分辨方法中非相關(guān)信源陣列導(dǎo)向矢量與噪聲子空間正交關(guān)系特性，實(shí)現(xiàn)非相關(guān)信源數(shù)目的估計(jì)，再構(gòu)造僅包含相干源信息的差分矩陣，實(shí)現(xiàn)相干源數(shù)目的估計(jì)。該算法通過(guò)構(gòu)造差分矩陣，消除了噪聲的影響，將相干源與非相關(guān)源的估計(jì)分隔開(kāi)。

實(shí)驗(yàn)結(jié)果表明：1)相比傳統(tǒng)的空間平滑類算法、矩陣重構(gòu)類算法以及SDS算法，本文算法在快拍數(shù)小和信噪比低的情況下依然能夠準(zhǔn)確的估計(jì)信源數(shù)目。單組相干源時(shí)，當(dāng)快拍數(shù)為200的情況下，信噪比為2dB時(shí)，成功檢測(cè)概率達(dá)到98%以上。當(dāng)信噪比為15dB的情況下，快拍數(shù)為20時(shí)成功檢測(cè)概率達(dá)到99%以上；2)當(dāng)信源角度接近時(shí)算法依舊有很好的性能。在快拍數(shù)為200的情況下，常規(guī)信源數(shù)估計(jì)算法在信源角度接近時(shí)，信噪比達(dá)到30dB時(shí)，成功檢測(cè)率也只能達(dá)到60%，本文算法，當(dāng)信噪比為5dB時(shí)，成功檢測(cè)率能達(dá)到98%以上；3)將非相關(guān)信源與相干信源分開(kāi)檢測(cè)，算法的信源承載能力較強(qiáng)。常規(guī)信源數(shù)估計(jì)算法都會(huì)損失陣列孔徑，本文算法將非相關(guān)信源與相干信源分開(kāi)分辨，重復(fù)利用陣列接收數(shù)據(jù)，具有更強(qiáng)的信源承載能力及陣元節(jié)省能力，當(dāng)陣元數(shù)為13時(shí)，可估計(jì)的信源數(shù)與陣元數(shù)相同。