高靈敏度感應(yīng)式磁傳感器測(cè)量誤差校正算法

張士榮，郭 強(qiáng)

(1. 江蘇理工學(xué)院，江蘇 常州 213001；2. 南京理工大學(xué)，江蘇 南京 210094)

1 引言

電磁波探測(cè)技術(shù)是一種發(fā)展成熟的地質(zhì)勘測(cè)方式，現(xiàn)階段，相關(guān)企業(yè)與研究人員開發(fā)出一系列相關(guān)產(chǎn)品，例如大地電磁測(cè)深儀、瞬變電磁儀等[1]。低頻電磁波能應(yīng)用在地質(zhì)測(cè)量、地殼通信、磁場(chǎng)勘測(cè)和地球物理觀測(cè)等領(lǐng)域。傳統(tǒng)勘測(cè)通常運(yùn)用鋪設(shè)線圈方法接收信號(hào)，但因受到地理空間約束，鋪設(shè)大量線圈給測(cè)量工作帶來極大不便[2-3]。高靈敏度感應(yīng)式磁傳感器能有效解決上述問題，在縮短體積的同時(shí)完成相等甚至更高的精準(zhǔn)度，在電磁波應(yīng)用中擁有舉足輕重的地位。

考慮到不同環(huán)境下由于工藝及安全水準(zhǔn)等原因，高靈敏度感應(yīng)式磁傳感器有時(shí)會(huì)產(chǎn)生偏移誤差。徐祥[4]等人提出基于自適應(yīng)參數(shù)估計(jì)的磁傳感器實(shí)時(shí)校正算法，對(duì)參數(shù)進(jìn)行實(shí)時(shí)估計(jì)和處理，構(gòu)建基于模值的參數(shù)估計(jì)方程，分析參數(shù)模型噪聲特性，針對(duì)非高斯?fàn)顟B(tài)相關(guān)噪聲提出采用自適應(yīng)參數(shù)估計(jì)方法，完成磁傳感器誤差的校正。但該算法對(duì)測(cè)量誤差因素考慮較少，難以保證校正結(jié)果的可靠性；王鵬飛[5]等人設(shè)計(jì)了基于誤差分離的矢量校準(zhǔn)算法，用于感應(yīng)式磁傳感器正交性校正。構(gòu)建正交性校正矢量校準(zhǔn)數(shù)學(xué)模型，對(duì)校正過程中的安裝誤差采取誤差項(xiàng)分離校正，融合卡爾曼濾波與最小二乘法求解模型參數(shù)，獲得正交性校正矩陣。但該算法的計(jì)算耗時(shí)較長(zhǎng)，證明其實(shí)時(shí)性較差。

針對(duì)傳統(tǒng)方法存在的不足，本文建立一種基于改進(jìn)遺傳算法的測(cè)量誤差校正算法。首先詳細(xì)分析高靈敏度感應(yīng)式磁傳感器工作機(jī)理和靈敏度影響元素，分類測(cè)量誤差來源，創(chuàng)建磁傳感器誤差模型，運(yùn)用自適應(yīng)方法完善遺傳算法內(nèi)的交叉算子和變異算子，實(shí)現(xiàn)高精度測(cè)量誤差校正目標(biāo)。

2 高靈敏度感應(yīng)式磁傳感器靈敏度分析

在感應(yīng)式磁傳感器內(nèi)起到關(guān)鍵作用的是線圈與磁芯，繞制的線圈用于感應(yīng)穿過其內(nèi)部磁通量的變化，從而生成感應(yīng)電動(dòng)勢(shì)。通過引入高磁導(dǎo)率的磁芯，能把信號(hào)增強(qiáng)若干倍。磁傳感器外磁場(chǎng)發(fā)生改變時(shí)，線圈軸線和磁場(chǎng)平行方向獲得的感應(yīng)電壓為

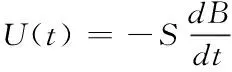
(1)

其中，S是繞制線圈的有效面積，B表示外磁場(chǎng)的磁感應(yīng)強(qiáng)度，負(fù)號(hào)是感應(yīng)電壓方向。如果變化的外磁場(chǎng)是正弦信號(hào)，則存在

B=B0sinωt

(2)

設(shè)定后級(jí)放大器的放大倍數(shù)是A，線圈匝數(shù)是n，磁芯有效導(dǎo)磁率是μa，繞制線圈有效面積計(jì)算公式描述為

S=ns0μaA

(3)

磁傳感器感應(yīng)電動(dòng)勢(shì)絕對(duì)值為

|E|=|2πens0μaAB0cosωt|

(4)

通過式(4)可以看出，感應(yīng)電壓和信號(hào)頻率e、線圈匝數(shù)n、骨架橫截面積s0、導(dǎo)磁率μa成正比，測(cè)量誤差校正可從這幾個(gè)參數(shù)入手。

電磁波在大地電磁勘測(cè)中傳播時(shí)，會(huì)有很多損耗，且低頻干擾信號(hào)強(qiáng)[6]。針對(duì)低頻弱信號(hào)，怎樣增強(qiáng)靈敏度是傳感器設(shè)計(jì)的重點(diǎn)。

倘若磁場(chǎng)信號(hào)是正弦波信號(hào)，傳感器附帶有增益是前置放大器，感應(yīng)線圈靈敏度是線圈在單位磁感應(yīng)強(qiáng)度改變中所呈現(xiàn)的感應(yīng)電動(dòng)勢(shì)，則可將靈敏度運(yùn)算公式描述成

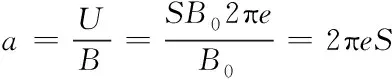
(5)

通過式(5)可知，在相同頻率情況下，靈敏度和S成正比。因此，提高有效面積是增強(qiáng)靈敏度的可靠路徑。針對(duì)骨架固定傳感器，有效導(dǎo)磁率取決于磁芯材料與長(zhǎng)徑比，將有效導(dǎo)磁率記作

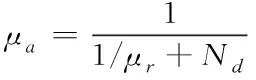
(6)

其中

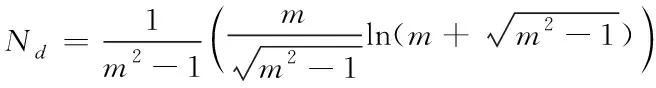
(7)

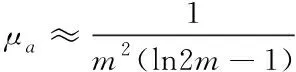
(8)

其中，μr表示相對(duì)磁導(dǎo)率，Nd是退磁因子，L是磁芯長(zhǎng)度，d是磁芯直徑。

3 測(cè)量誤差模型構(gòu)建

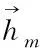
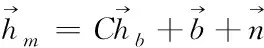
(9)

式中

C=CsCηCα

(10)

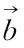
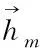
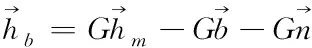
(11)

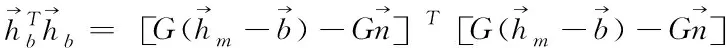
(12)

理論狀況下，感應(yīng)式磁傳感器三個(gè)向量在不同狀態(tài)下的值會(huì)在原點(diǎn)組成一個(gè)球心，半徑是測(cè)量區(qū)域地磁場(chǎng)標(biāo)量值的某個(gè)球面。

針對(duì)測(cè)量值大小，根據(jù)式(12)中可知，不同狀態(tài)下的全部測(cè)量值都被收斂在一個(gè)橢球面內(nèi)[8]。而硬鐵誤差劃定了橢球中間方位，軟鐵誤差與標(biāo)度系數(shù)誤差可以改變橢球長(zhǎng)短軸及扁率，而橢球長(zhǎng)軸指向則取決于裝配弧度誤差與軟鐵誤差。

讓?duì)Ｖ禎M足下列約束：

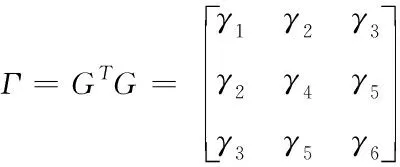
(13)

結(jié)合式(12)可得到N組測(cè)量方程的線性模式

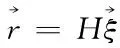
(14)

由于式(14)內(nèi)H具有噪聲，使用總體最小二乘法對(duì)ξ進(jìn)行估計(jì)[9]，得到

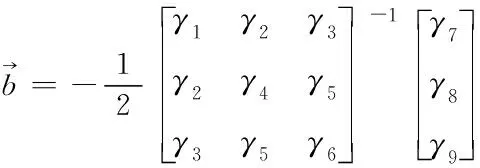
(15)

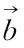
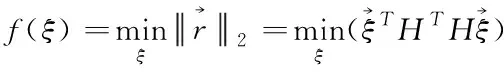
(16)

4 改進(jìn)遺傳算法下的測(cè)量誤差校正

從高靈敏度感應(yīng)式磁傳感器原理分析中可知，需要優(yōu)化的參數(shù)個(gè)數(shù)很多，很難尋找到最優(yōu)值，需要引用全新的計(jì)算方式。因此，本文采用遺傳算法實(shí)現(xiàn)參數(shù)最優(yōu)處理。

遺傳算法是一種擬照大自然生物演化過程的高隨機(jī)性搜尋手段，目標(biāo)函數(shù)無需連貫，計(jì)算簡(jiǎn)便，具備很強(qiáng)的魯棒性，在組合優(yōu)化、模式識(shí)別等領(lǐng)域得到充分運(yùn)用[10]。融合感應(yīng)式磁傳感器校正參數(shù)求解，完成改進(jìn)遺傳算法設(shè)計(jì)，將其代入測(cè)量誤差模型內(nèi)，實(shí)現(xiàn)高精度測(cè)量目標(biāo)。

設(shè)定一個(gè)誤差函數(shù)f

f=min[max(|Bj|-|Bs|)]

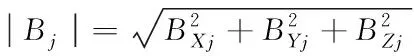
(17)

其中，f為包含信號(hào)頻率e、線圈匝數(shù)n、骨架橫截面積s0、導(dǎo)磁率μa的函數(shù)，|Bs|為設(shè)定的外界標(biāo)準(zhǔn)磁場(chǎng)模值，|Bj|為感應(yīng)式磁傳感器在姿態(tài)j下測(cè)量修正值的模。

測(cè)量誤差校正的目標(biāo)是探尋式(17)中的最小值，在遺傳算法內(nèi)個(gè)體函數(shù)值越低適應(yīng)度越高。把式(17)當(dāng)作適應(yīng)度函數(shù)，把e、n、s0和μa引入適應(yīng)度函數(shù)，函數(shù)值越低，個(gè)體適應(yīng)度越高，存活概率越高。

基于此，擇優(yōu)處理使用交叉、變異及選擇等有關(guān)算子。選擇算子是遺傳算法的典型算子之一，該算子從上一代種群內(nèi)剔除適應(yīng)度小的個(gè)體，盡可能保留適應(yīng)度高個(gè)體，組成若干能夠繁衍后代的子群體，實(shí)現(xiàn)模擬自然界優(yōu)勝劣汰機(jī)制目標(biāo)。

交叉算子能有效獲得新一代的個(gè)體形式，新個(gè)體具備父輩個(gè)體優(yōu)良特征，可達(dá)到算法全局搜尋目標(biāo)。但在實(shí)際操作中，若交叉概率過高，會(huì)破壞群體內(nèi)的良好模式，倘若交叉概率值過低，新個(gè)體生成的速率會(huì)變得緩慢，因此要嚴(yán)格控制交叉算子取值。

在傳統(tǒng)遺傳算法計(jì)算過程中，交叉概率一般任意選擇一個(gè)很高的值，而變異概率通常情況下會(huì)很低。交叉概率Pc取值范圍在0.25～0.88之間，變異概率Pm取值范圍是0.01～0.15，具有很強(qiáng)的盲目性。

在明確遺傳算法內(nèi)關(guān)于交叉算子與變異算子擇取盲目性前提下，使用改進(jìn)遺傳算法完成誤差校正任務(wù)[11]。運(yùn)算根本思路為：利用自適應(yīng)變化的交叉概率與變異概率替代原有概率，讓兩個(gè)概率伴隨種群進(jìn)化進(jìn)行對(duì)應(yīng)改變，完善后的方法能優(yōu)化全局搜尋能力與收斂效率，同時(shí)在搜尋流程后期方法收斂穩(wěn)定性依舊很好。

從種群內(nèi)獨(dú)立個(gè)體角度出發(fā)，交叉概率值高低應(yīng)該和個(gè)體適應(yīng)度值擁有密切關(guān)系；從種群全局進(jìn)化流程角度，伴隨進(jìn)化流程不斷深入，交叉概率要慢慢減少，直至最后變成一個(gè)平穩(wěn)值，防止對(duì)算法后續(xù)穩(wěn)定性造成不良影響，讓整個(gè)算法無法收斂或收斂速度慢。從生成全新個(gè)體方面考慮，種群全部個(gè)體在交叉運(yùn)作中要擁有相同地位，令遺傳算法無論處于搜尋空間的每個(gè)方位均具備勻稱性。

在真實(shí)操作中，如果要獲得滿足以上各個(gè)需求的交叉算子難度很高，創(chuàng)建僅和進(jìn)化代數(shù)有關(guān)，和個(gè)體適應(yīng)度無關(guān)聯(lián)的交叉概率運(yùn)算方法，具體計(jì)算過程為

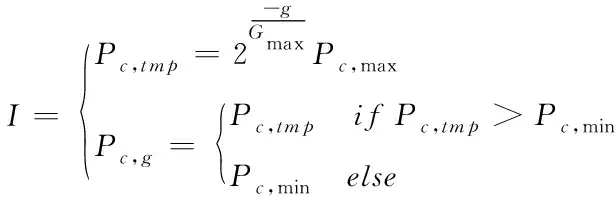
(18)

其中，Pc，tmp表示交叉概率中間參變量，Pc，max是設(shè)定的最大交叉概率，Pc，min是設(shè)定的最小交叉概率，Gmax代表最高進(jìn)化代數(shù)，g是目前進(jìn)化代數(shù)，0≤g≤Gmax，Pc，g是目前種群交叉概率。

比較理想的變異概率應(yīng)當(dāng)隨著個(gè)體優(yōu)劣不斷改變，也就是劣質(zhì)個(gè)體的變異概率變大[12]，為優(yōu)良個(gè)體賦予較低的變異概率。本文使用式(19)推導(dǎo)個(gè)體適應(yīng)度的自適應(yīng)變異概率

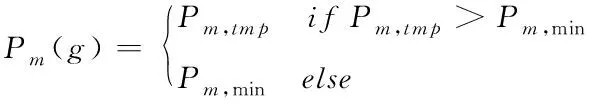
(19)

其中，Pm，tmp表示變異概率中間參變量，Pm，max是設(shè)定的最高變異概率，Pm，min是設(shè)定的最低變異概率，F(xiàn)max是個(gè)體的最佳適應(yīng)度值，F(xiàn)mean是個(gè)體適應(yīng)度均值，F(xiàn)(μ)是等待變異適應(yīng)度值，Pm(g)是現(xiàn)階段種群個(gè)體變異概率。

最后把式(18)與式(19)分別代入式(17)中的誤差函數(shù)，求解出準(zhǔn)確的測(cè)量誤差校正參數(shù)，提升高靈敏度感應(yīng)式磁傳感器的測(cè)量精度。

5 實(shí)驗(yàn)與分析

為驗(yàn)證上述高靈敏度感應(yīng)式磁傳感器測(cè)量誤差校正算法的有效性，分別通過數(shù)值仿真和實(shí)測(cè)數(shù)據(jù)對(duì)感應(yīng)式磁傳感器測(cè)量誤差校正算法的性能展開分析。其中，數(shù)值仿真用于明確算法參數(shù)估計(jì)的正確性，實(shí)測(cè)數(shù)據(jù)仿真用于證明算法真實(shí)有效性。

考慮到隨機(jī)測(cè)量噪聲影響，對(duì)算法實(shí)施Monte Carlo仿真，表1為應(yīng)用本文算法實(shí)施參數(shù)估計(jì)的平均結(jié)果。

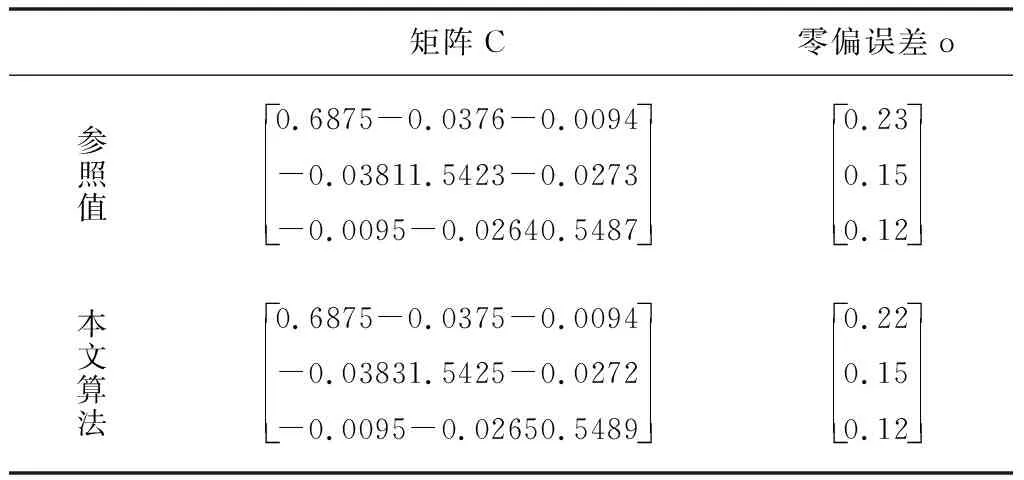
表1 模型參數(shù)設(shè)定

從表1中可知，本文算法可以準(zhǔn)確估計(jì)出參數(shù){C，o}，所得結(jié)果和參照值比較接近。

圖1為校正前后的測(cè)量重力場(chǎng)模值。從圖1中可知，在各種誤差綜合影響下，未校正數(shù)據(jù)展現(xiàn)出較大起伏的波動(dòng)，而本文算法校正后的測(cè)量模值都處于參照重力場(chǎng)模值周邊范圍。其原因在于本文算法使用改進(jìn)遺傳算法，準(zhǔn)確求解校正參數(shù)，有效增強(qiáng)所提方法整體校正精度。

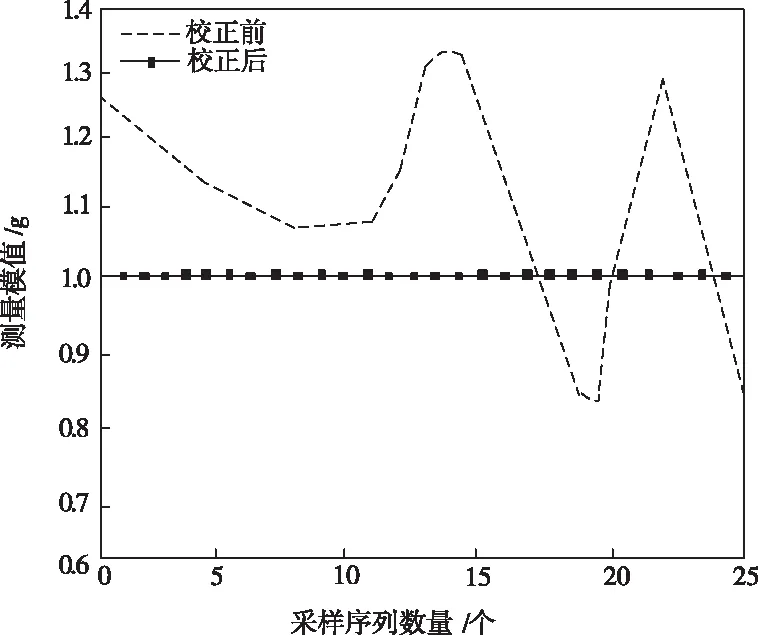
圖1 校正前后重力場(chǎng)模值和參照模值仿真結(jié)果對(duì)比

為深入探究本文算法有效性，使用感應(yīng)式數(shù)字加速度計(jì)進(jìn)行實(shí)測(cè)驗(yàn)證。測(cè)量數(shù)據(jù)利用微控制器從傳感器讀取，采樣頻率是150Hz，微控制器利用串行接口協(xié)議把數(shù)據(jù)轉(zhuǎn)發(fā)至上位機(jī)完成數(shù)據(jù)收集。把加速度計(jì)靜置15s時(shí)間，并求出其測(cè)量均值，得到不同姿態(tài)狀況下150組重力加速度測(cè)量數(shù)據(jù)。然后使用本文算法實(shí)施測(cè)量誤差校正，校正結(jié)果如圖2所示。

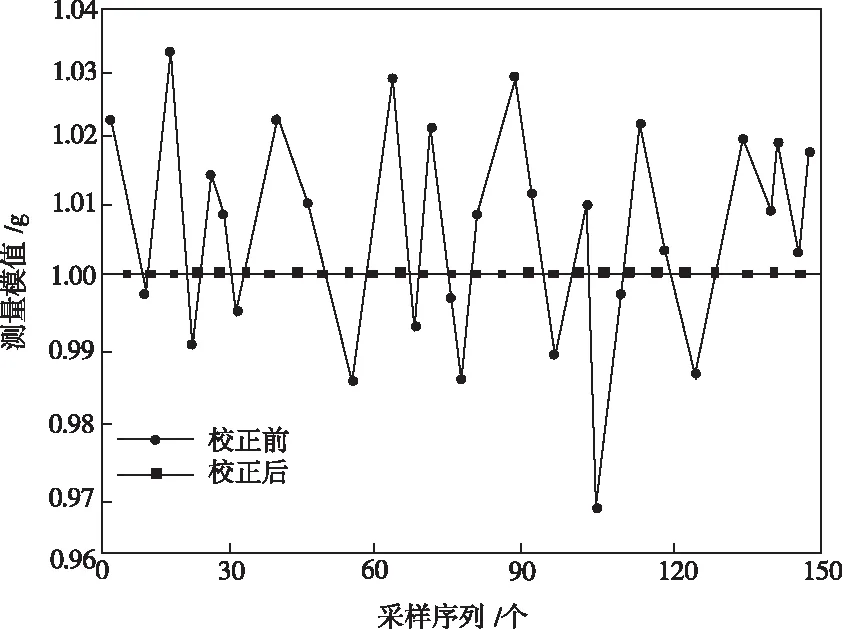
圖2 校正前后重力場(chǎng)模值和參照模值實(shí)測(cè)結(jié)果對(duì)比

根據(jù)圖2可以看出，校正前的加速度數(shù)據(jù)模值上下起伏比較劇烈，而本文算法校正后的加速度數(shù)據(jù)模值和參照重力場(chǎng)模值相差較小。證明應(yīng)用本文算法后，獲得的測(cè)量誤差校正參數(shù)合理、有效。

6 結(jié)語

面向不同環(huán)境因素下導(dǎo)致的磁傳感器測(cè)量誤差問題，本研究提出一種基于改進(jìn)遺傳算法的測(cè)量誤差校正算法。該算法具有優(yōu)秀的校正精度、魯棒性強(qiáng)、操作簡(jiǎn)便的優(yōu)勢(shì)，能夠?yàn)榇蟮仉姶艤y(cè)深勘探領(lǐng)域提供更加可靠的數(shù)據(jù)資源。但在改進(jìn)遺傳算法步驟中，沒有考慮選擇算子染色體變化規(guī)律在校正求解中的應(yīng)用，今后會(huì)對(duì)這一方面加以跟進(jìn)。