結合互信息的因子分析對患癌因素的分類仿真
孫士保,趙鵬程,李玉祥,李元穎
(1. 河南科技大學信息工程學院,河南 洛陽 471023;2. 河南科技大學臨床醫(yī)學院,河南 洛陽 471023)
1 引言
隨著“人工智能+醫(yī)療”技術的發(fā)展,智慧醫(yī)療越來越被人們所熟知和接受。人工智能(AI)正在越來越多地被開發(fā)用于治療和診斷以及對患病風險進行評估和分類[1]。Manogaran Gunasekara等人測量跨基因組DNA高維數(shù)據(jù)集來診斷癌癥,使用貝葉斯隱馬爾可夫模型(HMM)與高斯混合(GM)聚類方法進行處理[2]。廖志軍等人利用隨機森林分類算法提取mRNA特征應用于六種癌癥的診斷[3]。夏春秋通過低秩表示從高維基因數(shù)據(jù)中找到具有判別力的特征再對癌癥進行分類[4]。Moloud Abdar則是利用置信度加權投票方法和增強集合技術對早期乳腺癌進行診斷[5]。Subhashis Banerjee 等人在選擇重要特征的同時利用自適應神經(jīng)模糊分類器對腦瘤分類,達到85.83%的分類正確率[6]。
綜上所述的研究都是對患者進行診斷,但是在早期階段的大多數(shù)癌癥均沒有明顯癥狀,當診斷出癌癥時,早期治療的延誤會增加病患的致死率,導致無法挽回的后果。因此,在智慧醫(yī)療領域中迫切需要準確對早期患癌風險進行篩查,盡早的發(fā)現(xiàn)癌癥并進行治療,最大限度的延長患者的生命。研究者康桂霞使用ReliefF算法分析癌癥的最具辨別力的特征,通過決策樹來預測癌癥的風險[7]。Reedy Jill采用因子分析和指數(shù)分析比較3種膳食模式方法導致結直腸癌的風險[8]。王云溪應用因子分析和Logistics回歸模型分析胃潰瘍癌變的潛在預測因子[9]。面對早期癌癥數(shù)據(jù)這類高維復雜性數(shù)據(jù)集,在處理過程中,采取因子分析的主要是將具有錯綜復雜關系的變量(或特征)綜合為若干個因子,以解釋原始數(shù)據(jù)與因子之間的相互關系,達到特征選擇和降維的目的,以便算法模型的預測和分類效果有效,降低計算復雜度[10]。但是因子分析在計算因子得分時用到最小二乘法、極大似然法,在面對非線性關系時容易失效,使得分類效果欠佳。因子分析更傾向于描述原始變量之間的相關關系。
本文為解決傳統(tǒng)的因子分析特征選擇算法中(相關性矩陣)協(xié)方差矩陣只能夠衡量具有相關關系的特征。將互信息引入到因子分析中進行特征選擇,由于互信息能夠利用信息熵衡量特征與類別或者兩個特征之間依賴程度的強弱,展現(xiàn)出兩個特征間擁有共同信息的含量,并且不局限于線性關系[11]。從而更有效地對高維數(shù)據(jù)進行特征選擇,用以提高算法的分類精度。因此,提出一種結合互信息的因子分析對患癌因素的分類方法。人們可對早期癌癥風險因素進行分類,避免延誤最佳治療時機。
2 因子分析
因子分析是當前特征選擇中應用最為廣泛的方法之一[12]。在高維數(shù)據(jù)中,因子分析通過多個特征間協(xié)方差矩陣的內部依賴性關系,找到能夠反映出所有特征主要信息的公因子。
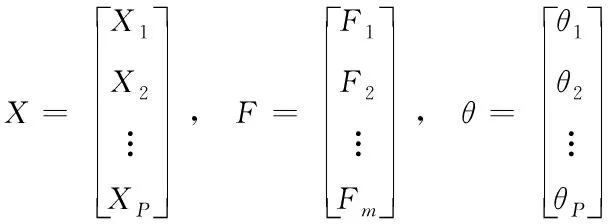
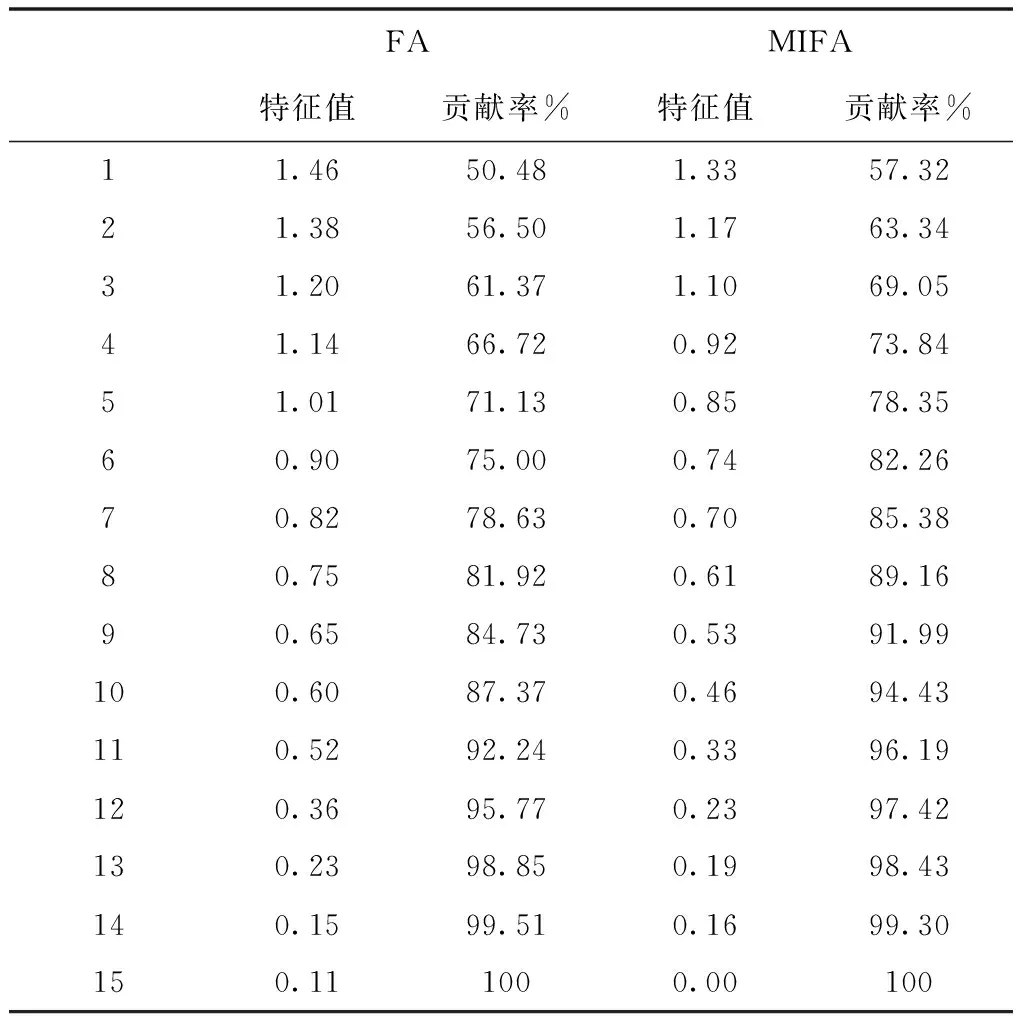
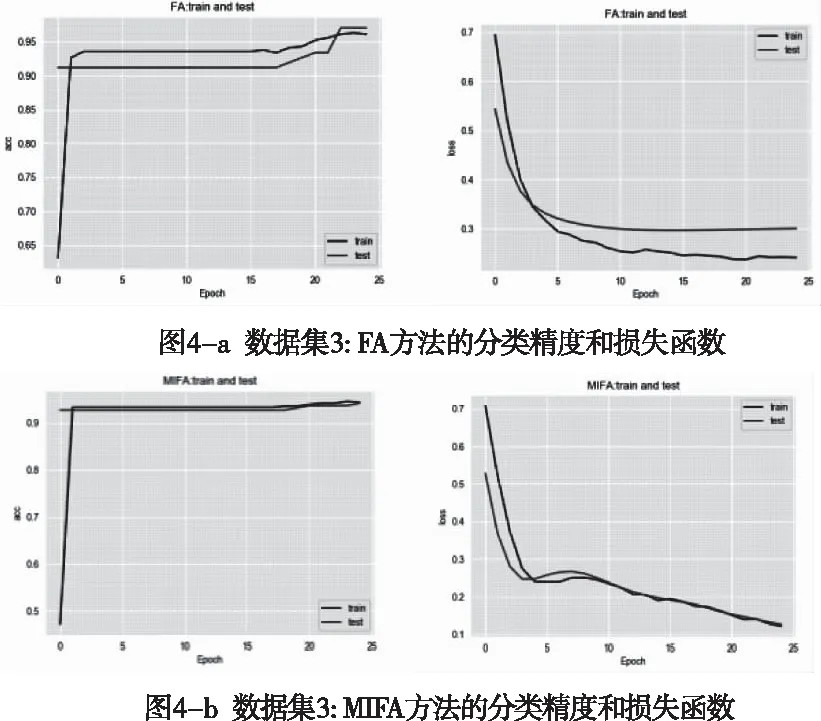
假設有n個樣本量,p個指標(特征),X=(X1,X2,…Xp)T為隨機特征,其中協(xié)方差矩陣cov(x)=Z;可得出本假設的公共因子為F=(F1,F(xiàn)2,…Fm,)T(m (1) 其中θp為特殊因子,則A=(aij) 稱為因子載荷矩陣,aij為因子載荷(loading),實質表示Xi依賴因子Fj的程度[13]。該因子分析模型滿足正交,矩陣形式具體表示為 (2) (3) 因子模型簡單表示 X=AF+θ (4) 式中cov(F,θ)=0, 公共因子和特殊因子滿足不相關的條件。針對高維數(shù)據(jù)集,使用因子分析進行降維,特征之間需具有線性相關性,得出的各個公共因子應具有可解釋性。因子分析算法如下所示。 Input: 原數(shù)據(jù)集N 特征X={X1,X2…Xn} output: 因子模型X=AF+θ 1)標準化原數(shù)據(jù)集N; 2)計算高維數(shù)據(jù)集N中特征X間協(xié)方差陣; 3)若KMO∈[0,1] 并KMO≥0.5則輸出F=[F1,F(xiàn)2…Fn]; 4)通過因子旋轉,使得公共因子F更具有解釋性; 5)對因子F計算得分,轉換為因子載荷A=(A1,A2,…,Am),并得出特殊因子θ=[θ1,θ2…θn]; 6)輸出因子模型:X=AF+θ. 在信息和概率論中,兩個隨機變量的互信息(Mutual Information, MI)衡量它們之間相互依賴的程度,解釋為兩個特征之間共同擁有信息的含量[14]。互信息具有兩個顯著的優(yōu)點: 1)能夠對隨機變量間復雜的關系進行處理,包括處理非線性關系,保證特征與類別間在未知關系情況下依然有效; 2)不局限于實值隨機變量,并在特征空間的變換情況下互信息的值不會改變,保證了在任意階段都可以準確度量特征間的關系。 一般地,兩個變量X和Y的互信息[15]可以定義為 (5) 其中p(x,y)是X和Y的聯(lián)合概率分布函數(shù),p(x)和p(y)分別是它們的邊緣概率分布函數(shù)。若I(X;Y)=0當且僅當X和Y是獨立的隨機變量,可知 p(x,y)=p(x)p(y) (6) 因此 (7) 綜上所述,互信息具有非負性I(X;Y)≥0和對稱性I(X;Y)=I(Y;X)。X和Y兩者依賴程度越高,I(X;Y)的值就越大,類別與特征間包含的共有信息也就越多,反之,則類別與特征相互獨立,不存在任何共同信息。 結合互信息的因子分析算法框架如圖1所示。因子分析中使用協(xié)方差矩陣只能反映出特征間的相關性,即為線性關系,無法有效的評價特征間的非線性關系,而算法的思想就是引入互信息,利用其評估特征間的共有信息這樣的特異性來優(yōu)化特征選擇的處理過程,使得算法不局限于線性關系。 圖1 結合互信息的因子分析算法框架圖 首先,對原數(shù)據(jù)的p個指標標準化處理,消除特征在量綱上的影響。根據(jù)標準化后的數(shù)據(jù)矩陣求出協(xié)方差矩陣Z。定義ZI(X;Y)為原數(shù)據(jù)的互信息陣,使用拉格朗日因子法得到協(xié)方差陣對應的特征值的特征向量。原數(shù)據(jù)特征值為λ1,λ2,…λp,單位特征向量U為 (8) (9) 因此,在實際因子分析過程中采用互信息來替代協(xié)方差陣,本文提出一種結合互信息的因子分析(MIFA)特征選擇算法用于患癌風險因素的分類。得到因子模型為 (10) ψ是Z的特征值構成的對角陣。由非負性I(X;Y)≥0和互信息對稱性I(X;Y)=I(Y;X)可知,不論是互信息(非對角線元素表示兩個特征間的互信息)或自信息(信息熵,對角線元素表示的變量)均為實數(shù),ZI(X;Y)為非負實數(shù)對稱矩陣。 (11) 表示因子分析中公因子對特征的Xi總方差所做出的貢獻,取值在0~100%之間,數(shù)值越大,說明該特征能被公因子解釋的信息量越大。最終,選擇貢獻率為85%以上的前M個公因子作為原數(shù)據(jù)新特征,統(tǒng)計學上指標達到85%即可認為這些因子包含了全部特征的原始主要信息。 Input: 數(shù)據(jù)集D output:M個新特征 1)標準化數(shù)據(jù)集D; 2)計算求得協(xié)方差矩陣Z; 3)Z轉換為ZI(X;Y)互信息陣,并求得特征值λ={λ1,λ2,…λp}; 本章節(jié)首先給出實驗數(shù)據(jù)集的信息、實驗相關設定和算法性能評價指標,然后分為3組實驗對結果分析,并與文獻[7]中所采用ReliefF進行特征選擇的多個分類算法進行比較。 仿真數(shù)據(jù)來自于開源的機器學習數(shù)據(jù)庫UCI,選取了高維度的宮頸癌(Cervical)、乳腺癌(Breast)和肝癌(HCC)數(shù)據(jù)集,均屬于可預防的癌癥類型,早期發(fā)現(xiàn)患癌風險并進行治療即可完全治愈。因此數(shù)據(jù)集作為對患癌風險因素的分類具有很好的借鑒作用,且高維特征符合實驗要求,數(shù)據(jù)集信息如表1所示。仿真使用Python語言在Ubuntu系統(tǒng)(CPU Intel Corei5/8GRAM)中運行。 表1 實驗數(shù)據(jù)集信息 實驗組中神經(jīng)網(wǎng)絡分類算法評估學習模型選擇常用的兩個參數(shù):分類正確率accuracy和損失函數(shù)loss。其中損失函數(shù)loss的表達式為 Loss=-ln(Pz)=-ln(Pcorrect) (12) Pz是將樣本分配到類別Z的概率,即正確分類概率Pcorrect。當對于一個迭代(Epoch)中含有無窮多個樣本時: Loss=E(-ln(accuracy)) (13) 即 accuracy=e-Loss (14) 在神經(jīng)網(wǎng)絡中通常可知accuracy數(shù)值越高,loss越小,模型性能越好。 實驗組1:本實驗組在用于患癌風險因素分類時,對三個數(shù)據(jù)集進行公因子提取。比較了通過FA與MIFA從原數(shù)據(jù)集提取15個(累積貢獻率>50%)的因子特征值和累積方差貢獻率,如表2、表3和表4所示。 表2 數(shù)據(jù)集1:FA和MIFA求得的因子信息 通過表2可以得出,以因子累積貢獻率等于85%作為指標,以FA作為特征選擇算法需要9個新特征才能解釋原數(shù)據(jù)全部信息,而采用MIFA則只需要5個新特征即可包含原來的所以特征信息。從可解釋性方面可以看出,在相同維度下,F(xiàn)A的因子貢獻率低于MIFA,例如同樣在公因子5的情況下,F(xiàn)A的貢獻率為70.39%,而MIFA的貢獻率為85.47%。 同樣地,由表3可以發(fā)現(xiàn)采用FA進行特征公因子選擇需要8個公因子數(shù)量,累積貢獻率大于85%,而使用MIFA方法僅需要5個公因子即可解釋原始數(shù)據(jù)集實際意義。同理,通過表4可以清楚看出對于因子的可解釋性,相同維度下,例如在公因子8的情況下,因子分析的貢獻率為81.92%,而結合互信息的因子分析的貢獻率則為89.16%。 表3 數(shù)據(jù)集2:FA和MIFA求得的因子信息 表4 數(shù)據(jù)集3:FA和MIFA求得的因子信息 綜上所述,即可證明MIFA降低的數(shù)據(jù)維度量和公因子解釋性高于傳統(tǒng)的因子分析方法,有利于模型的分類正確性。實驗組2將采用常用的分類算法進一步驗證。 實驗組2:以實驗組1降維之后的數(shù)據(jù)集作為分類算法的輸入進行仿真。本組實驗以常用的神經(jīng)網(wǎng)絡(ANN)作為分類器來驗證因子分析(FA)與結合互信息的因子分析(MIFA)得到的公因子對宮頸癌活檢進行預測。神經(jīng)網(wǎng)絡分類器包含有輸入層(Input layer)、隱藏層(Hidden layer)、輸出層(Output layer),激勵函數(shù)設置為sigmoid;采用十折交叉驗證法。 通過圖2-a看到FA訓練集和檢測集產(chǎn)生很大的過擬合現(xiàn)象,可以看到檢測集的精確度只有89%左右。而通過圖2-b可以明顯看出MIFA的模型過擬合現(xiàn)象被解決,檢測集的精確度逐漸達到95%,有較大的提升。通過圖3-a和3-b明顯看出FA的損失函數(shù)并未趨于收斂,而MIFA的損失函數(shù)在完成10次迭代后快速收斂,最終的損失函數(shù)值只有0.1138,說明算法達到實驗效果。 同樣可以看出對于數(shù)據(jù)集2和3所得出的分類精度和損失函數(shù)。如圖3和4所示,數(shù)據(jù)集2、3在迭代15-20次時精確度出現(xiàn)很大波動,產(chǎn)生較大過擬合,檢測集精度過低,相對的損失函數(shù)也未趨于收斂,特別地,對于數(shù)據(jù)集3檢測集的損失函數(shù)過大,算法性能較差。而MIFA則在處理高維度癌癥數(shù)據(jù)集產(chǎn)生較好的分類效果,神經(jīng)網(wǎng)絡循環(huán)迭代10次后損失函數(shù)趨近于收斂,分類精度分別為95.96%和96.13%,損失函數(shù)為0.1341和0.1216。 實驗組3 為了客觀展示實驗結果,通過10次十字交叉法驗證,如圖5所示。清楚地看出針對高維數(shù)據(jù)集采用MIFA計算出的公因子作為分類器輸入項所得到的分類正確率高于FA方法。 圖5 數(shù)據(jù)集交叉驗證分類精度對比 綜上所述,證明了MIFA特征選擇較傳統(tǒng)FA方法性能更加優(yōu)越。而在文獻[7]中康桂霞采用ReliefF特征選擇對早期癌癥風險因素進行分類,通過決策樹DT和支持向量機SVM以及BP神經(jīng)網(wǎng)絡構建模型得出的分類精確度如表5所示。可以清楚地發(fā)現(xiàn)本文提出的MIFA算法均值高于文獻[7]所示的ReliefF特征選擇算法,證明了算法的有效性。 表5 分類精確度對比 本文提出了結合互信息的因子分析對患癌因素的分類算法,并進行仿真。算法在進行特征選擇的時利用互信息處理非線性關系的優(yōu)點,使用協(xié)方差陣轉換為互信息陣從而確定公因子特征達到降維目的。采用神經(jīng)網(wǎng)絡作為分類器,三組數(shù)據(jù)分類精度分別達到96.51%、95.96%和96.13%。仿真結果表明在處理具有復雜性和高維度的癌癥數(shù)據(jù)效果顯著。今后的研究工作將主要集中在如何結合條件互信息與因子分析對高維的醫(yī)學數(shù)據(jù)集進行處理。

3 結合互信息的因子分析對患癌因素的分類算法
3.1 互信息相關知識
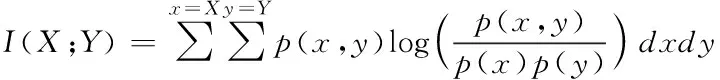

3.2 算法描述與分析



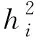
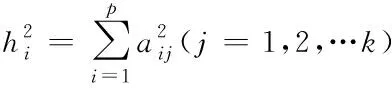
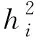

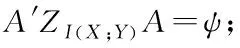



4 實驗分析
4.1 實驗信息

4.2 實驗結果與分析






5 結束語

