基于FLAC3D的巖土預應力錨固支護數值模擬

盛曉杰，陸漢光

(四川大學錦江學院，四川 眉山 620860)

1 引言

中國是一個多山的國家，在山區建設、鐵路、公路與房屋建筑中通常會涉及到邊坡加固的問題。當前，邊坡加固方法內錨固支護即一種原位巖土體加固的方法，其已經成為了使用最為廣泛的直接加固方法之一。錨固支護，包括預應力錨固支護，其可以充分發揮巖土體能量，改善巖土體不利的受力情況，調動與提升巖土的自身強度與自穩能力，進而能夠大大縮減支護架構的自重、節省工程材料、減少工期。

但由于錨固支護機理方面的研究依然滯后于工程實踐，而大多數設計只能夠依靠經驗與工程類比法進行確定，但是預應力錨固支護工程的安全性與經濟性很大程度上都取決于錨固之間的相互作用，因此憑借經驗或工程類比法來評定錨固支護的構建好壞，是存在誤差的。所以，怎樣合理的預測預應力錨固支護效應，同時使其在現實工程的設計內得到體現，這是一個非常關鍵的問題。

因此本文提出一種基于FLAC3D的巖土預應力錨固支護數值模擬方法，通過巖土的破壞準則與屈服準則構建巖土彈塑性模型，并得到巖土變形時產生的變量，模擬巖土與接觸關系，構建預應力錨固支護模型，憑借有限差分軟件LLAC3D構建有限差分模型，依靠該模型對預應力錨固支護進行數值模擬，提高了預應力錨固支護的加固效果。

2 FLAC3D下巖土預應力錨固支護數值模擬計算

三維快速拉格朗日(Fast Lagrang-ian Anlysis of Continua 3 Dimension，FLAC3D)通過美國Itasca公司研發出的連續介質力學分析軟件，該軟件能夠較好模擬巖土體或其余材料的三維力學行為，在材料的彈塑性分析、預應力變化、大變形分析、施工過程以及錨固支護結構的模擬等方面存在其獨到的優勢。

巖石變形性質的特征即模量與預應力之間存在非常顯著的水平關聯，其加載模量要比卸載模量低，本文憑借FLAC3D，來模擬巖土的三維力學行為，同時依靠彈塑性理論進行研究，巖土本體總的形變可以分成彈性變形以及塑性變形兩種，利用虎克定律對彈性變形進行計算，再采用塑性理念對塑性變形計算，而巖土產生破壞變形與塑性變形的兩種分界點就是屈服準則與破壞準則，所以需要對巖土本體的彈塑性本構進行關聯研究，因此就需要搭建材料來構建屈服與破壞的條件與準則。

2.1 巖石的本構模型

2.1.1 破壞準則

在巖土出現破壞之后，其會隨著時間的推進出現擴大，與產生破壞之前，呈現不同的形式，給出一種評定破壞與否的指標，就是破壞準則[1]，構建巖土的本構關聯，巖土的破壞會取決于預應力的狀態，因此破壞準則可以通過式(1)進行描述

f(σij)=kf

(1)

式中，f(σij)代表預應力分量的函數，就是破壞函數，kf代表經過測試確準的常數。

2.1.2 屈服準則

材料的受力變形，在預應力越過了某種界限時，材料會出現塑性變形，預應力的曲線呈非線性轉變，這就說明材料出現了屈服[2]情況，根據以往的實驗證明，屈服的主要原因是通過預應力的當前狀況取決的，針對復雜的預應力，在預應力分量的某個函數組合大于擬定的閾值時，材料就會產生屈服，通過以下表達式能夠描述成

f(σij)=k

(2)

其中，f(σij)表示屈服函數，其同等于破壞函數，并且和坐標沒有任何關聯，所以該函數能夠作為預應力的不變量函數，k表示和預應力歷史存在關聯的常數，也能夠描述為預應力歷史出現變化的變量。

2.1.3 彈塑性模型

巖土是結構非常復雜的復合體，在巖土工程資料中，預應力巖土力學[3]存在兩種較為關鍵的參數即：粘聚力c與摩擦角φ。本文通過破壞準則為基礎的彈塑性模型對這兩種參數進行處理，為了提升這兩種參數的使用情況，并且可以更好的對巖土的真實狀況進行反映，在平面應變的條件下，將破壞與屈服準則進行比較，就能夠獲得

(3)

(4)

這樣，經過將兩種破壞準則相結合，就能夠經過摩擦角φ與粘聚力c，計算獲得a與k這兩個參數，并通過這兩個參數獲取相對穩定的破壞準則。

彈塑性模型[4]是一種較為理想的模型，采用魯克一普拉格屈服準則進行微分后能夠獲得

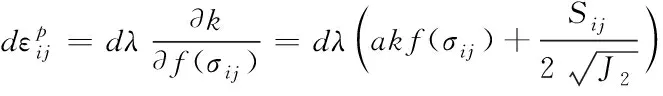
(5)

假如將彈性增量狀態也考慮其中，那么根據屈服準則和破壞準則構建彈塑性模型，其表達式為

(6)

式(5)與(6)中，Sij表示預應力偏量，G為剪切模量，V表示泊松比；e與k表示廣義米塞斯準則的兩種測試參數，I1與J2表示第二應力的偏量不變量與第一應力的不變量。

2.2 預應力錨固支護架構與力學模型

通過有限元對錨固支護進行分析時，首先需要劃分錨固支護的單元，其最為常見的方法有兩種即：把整體架構擬定為向異性的負荷材料，并不會映射出錨固支護架構間的作用，此方法不會呈現錨固支護[5]架構受力狀態，而另一種即把它們分開考慮，這樣更能反映錨固支護的真實受力情況。

但目前對巖石預應力的處理方式存在不同，這就導致數值模擬存在較大的爭議，因此本文將延時預應力錨固支護劃分成以下單元：巖土單元、由錨固與支護簡化成的梁單元和桿單元以及面層單元。

高強預應力下的錨固支護通過高強桿體、托盤、讓壓管與螺母等組件構成。和普通的錨桿體系[6]相比，巖土錨固支護在錨桿尾端添加了一種存在讓壓能力的讓壓管。憑借巖土狀況的不同，讓壓管能夠擬定制造為不同的規格。同時把該錨固支護的軸向應力-應變關系分成5種階段。

憑借試驗結果，高強預應力讓壓錨固支護的軸向應力-應變關系如圖1所示。

圖1 錨固支護軸向應力-應變關系

根據錨固支護軸向應力-應變關系，能夠通過式(7)所示的分段函數進行描述：

(7)

錨固支護橫向剪應力-剪應變關系[7]通過以下的本構關聯進行模擬，其關系曲線如圖2所示。

圖2 錨固支護剪應力-剪應變關系

根據上述錨固支護剪應力-剪應變關系構建本構關聯

(8)

其中，τbp代表高強預應力讓壓錨固支護的極限抗剪程度。

2.2.1 巖土與接觸關系模擬

巖土的非線性特征與變形特性通過上述的彈塑性模型模擬，其屈服準則的描述如下

(9)

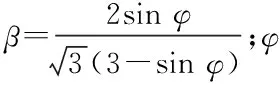
在巖土工程錨固支護體系內存在巖層層面間的接觸關聯以及錨固和周邊巖土接觸的關系。錨固支護和周圍巖土共同作用時，因為上覆巖土層壓力[8]作用于周圍巖土性質變形不協調，在周圍巖土層面間可能會產生豎向脫離狀況，此外，因為層間存在剪切作用，周圍巖土層面就會產生剪切錯動或是滑移等狀況。

錨固支護的桿體和周圍巖土間具有徑向接觸和切向接觸兩種狀況，接觸性能與錨固劑[9]可以提供的切向剛度與徑向剛度存在關聯。合理的數值模型可以較好的模擬巖土工程的開掘與周圍巖土變形過程內錨固支護體的所有接觸關系。

本文內周圍巖土層面接觸與錨固支護桿體的接觸關系通過接觸面對模型進行處理。層面接觸考慮層面閉合，同時無相對滑動、層面閉合且相對滑動與層面分離這三種狀況。

2.2.2 錨固支護模型與預應力施加方法

預應力讓壓錨固支護經過錨固段和周圍巖土發生作用，而錨固和周圍巖土不出現接觸，模型內，錨固使用兩節點支護單元[10]進行模擬，同時支護單元和周圍巖土完全脫離，那么不存在支護體和周圍巖土間的摩擦力，而是預應力在支護體傳遞過程中衰減。現實情況中，巖土和錨固劑材料接觸面上的剪切破壞是錨固段的主要破壞形式。錨固段的切向剪切程度和粘性系數、摩擦角與預計嵌入程度都存在關聯。隨著切向位移的提升，粘性系數與嵌入影響會慢慢縮小，摩擦[11]作用就會變成主要因素。

本文通過式(10)的雙折線模型來模擬錨固段的切向剪應力與剪應變之間存在的關聯

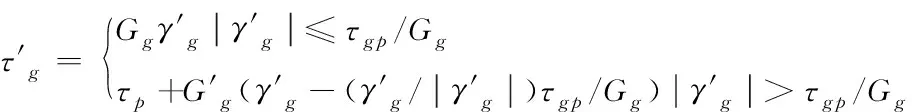
(10)

其中，τgp代表屈服剪應力，G′g代表剪應力大于屈服剪應力之后的剪切模量，取最小值。

擬定錨固托盤和巖土壁變形協調，托盤使用剛性塊單元進行模擬，剛性塊中間位置通過鋼臂進行約束，從而限制其轉動，預應力以均勻分布荷載作用[12]至托盤內。錨固支護的最終受力情況應該是預應力以及計算值的總和。

2.2.3 邊界條件設定

巖土變形與支護問題的有限元分析觸及兩類邊界條件，一種即邊界約束條件，另一種即邊界受力條件。憑借經驗，獲取一定的周圍巖土范圍，同時構建簡易的人工邊界，這樣能夠較好的模擬巖土的受力情況。

本文憑借圣維南原理與試算結果，豎向與橫向運算該區域，分別取巖土工程高度與寬度的8倍，同時擬定簡單人工邊界。邊界約束條件設定成：巖土頂邊界自由，同時作用有豎向地應力，巖土兩側邊界水平向約束，豎向自由，巖土底邊界設定成固定邊界。

地應力值考慮上覆周圍巖土自重，同時使用地應力平衡法施加，作用于頂邊界豎向的地應力，該地應力能夠憑借式(11)進行取值計算

(11)

其中，Ei與γi與hi分別代表第i層巖土的彈性模量、厚度與重力密度，n代表作用于巖土釘人工邊界中的巖土層層數，h1代表巖土直接頂巖土層厚度。

在獲取巖土兩側邊界處，周圍巖土需要存在一定的水平向位移，同時應作用水平地應力。但這部分變形在通過考察區域中的傳遞之后，對離邊界較遠額的巖土影響是非常小的，對于巖土變形與錨固支護效果分析是能夠接受的。

3 仿真數值模擬分析

為了證明FLAC3D算法對巖土錨固支護數值模擬的精確性，綜合某地區邊坡加固工程，使用有限差分軟件LLAC3D構建有限差分模型，憑借施工順序，對邊坡分級巖土錨固支護進行數值模擬。

3.1 基本假定

為了便于構建數值模擬分析模型，綜合該邊坡工程的現實錨固支護狀況，進行如下假定：

1)錨固支護架構與巖土預應力之間存在平面應變問題。

2)錨固、土釘以及周圍巖土、漿體完全粘結，滿足變形相容條件。

3)地下水埋藏較深，在模擬計算的過程內，不需要考慮地下水的干擾。

3.2 巖土工程概況與參數

巖土工程設定在某一已知數值的地區上，根據現場勘查資料現實，道路沿線底層主要通過雜填土、黃土狀粉圖與泥質沙巖等組成。道路沿線坡體高度為13～19m，坡度較陡，因為連續的降雨，多處填土與粉土邊坡已經產生了較為明顯的塌陷與崩落情況。加固邊坡即運輸車輛道路的永久性邊坡，安全等級為一級，局部地段為二級。

3.3 模擬結果分析

通過Matlab仿真軟件繪制錨固支護向正應力云圖。

通過圖3能夠看出，錨固支護張拉在周邊巖土內形成了一原型壓應力區，壓應力在錨固支護的中心最大，沿邊界慢慢縮小，沿軸向呈現高陡的拋物線形式分布。壓應力區的存在對于邊坡工程內開挖卸荷引起的松動區存在較大的改善效果，但對于較軟的巖土松動區可能會引起較大的預應力損失。憑借某軟巖土高邊坡預應力錨固支護張拉完成錨固支護張拉鎖定后預應力比對，對比結果如表1所示。

圖3 錨固支護向正應力云圖

表1 錨固支護張拉鎖定后預應力比對

根據表1中的數據可知，因為錨固支護所在位置巖土強度不同，最大預應力損失值達到了9%左右為了能夠更為清晰且簡易的表明本文方法的數值模擬效果，以某實際巖土預應力錨固支護加固邊坡工程為例，使用本文所提方法對邊坡有、無錨固支護情況下的坡體變形進行了數值模擬分析，同時和現場檢測結果進行了比對。

某運輸公路路埑高邊坡軸線開挖深度為70m，出露地層是灰巖以及泥巖互層。其巖土層面緩傾向路集方向。滑坡原因即順坡緩傾的泥巖層，軟弱容易變形，這是滑坡賦存的基礎地質條件，其模擬結果如圖4、5所示。

圖4 無錨固支護下工況下坡體位移模擬結果

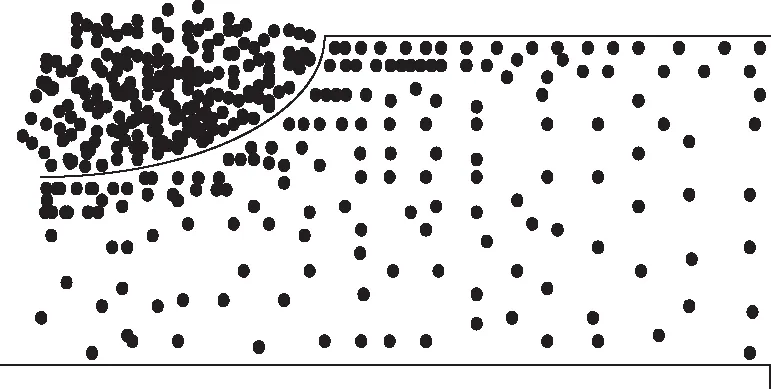
圖5 有錨固支護下工況下坡體位移模擬結果

通過圖4、5能夠看出，無支護工況下，在最后一級坡面開挖過程內，整體坡體產生塑性破壞，使得坡體產生整體滑動。而在預應力錨固支護情況下，坡體應力區范圍減少了約70%左右，較大的壓應力延伸至坡面附近。且能夠看出整個階段的張拉鎖定后預應力與LLAC3D模擬結果大致相同，證明該錨固支護工程是有效的。

4 結束語

為了能夠更為直觀的描述預應力錨固支護對巖土工程的加固效果，提出通過FLAC3D軟件構建有限差分模型完成對錨固支護數值的模擬。

通過實驗分析得出，所提數值模擬結果真實有效，在滿足施工要求的同時又極大程度的保障工程安全性。但由于錨固存在群錨固支護與單錨固支護的分別，而該方法無法做到對單體錨固支護進行精細的模擬，因此下一步需要研究的課題即：在該算法的基礎上，添加細分算法，依靠該算法將整體錨固支護，劃分成多個單一錨固支護，進而完成對單一錨固支護的數值模擬。