基于TLFK的單軸旋轉SINS在線自標定方法

胡 杰，嚴勇杰

(1. 中國電子科技集團公司第二十八研究所，江蘇 南京 210007；2. 空中交通管理系統與技術國家重點實驗室，江蘇 南京 210007)

1 引言

捷聯式慣性導航系統(Strapdown Inertial Navigation System， SINS)利用正交安裝的陀螺和加速度計敏感得到載體運動角速率和比力信息實時計算載體導航參數，具有全自主、全天候、隱蔽性強等優點，但是SINS中慣性測量單元(Inertial Measurement Unit， IMU)漂移會引起系統隨時間累積性誤差。目前提高SINS導航精度主要有2種途徑：一是提高IMU測量精度；二是采用系統級方法抑制IMU漂移引起的導航誤差。短期內提高IMU精度難度較大且成本高，系統級補償方法具有成本低、見效快等優點[1]。旋轉調制技術是一種常用的系統級誤差補償方法，自20世紀以來已經成為國內外高精度慣導領域主要研究方法之一[2-3]。國外旋轉式SINS已經廣泛應用于水面艦船、潛艇以及水下機器人，典型產品有Sperry公司研制的MK39系列單軸旋轉SINS、MK49系列和AN/WSN-7系列雙軸旋轉式SINS，均采用旋轉調制技術抑制慣性器件漂移引起的累積誤差[4-5]。自2002年起，我國相關研究機構也開始了旋轉式SINS的研究工作，國防科技大學于2007年研制出我國第一套旋轉式SINS，在實驗室靜態測試環境下，其位置誤差優于1 n mile/24h[6]。目前，東南大學[7]、北京航空航天大學[8]、哈爾濱工程大學[9]等高校也積極開展旋轉式SINS理論與樣機研制工作，取得了較大的研究成果。

單軸旋轉SINS中，方位軸的周期性旋轉調制抵消了水平方向上的IMU誤差對導航精度影響，其軸向IMU誤差引起的位置累積誤差依然存在，如軸向陀螺常值漂移為0.01°/h，緯度為45°時，純慣性導航24h后位置誤差約為10n mile，是高精度長航時SINS主要誤差源之一，為此許多學者對如何精確標校單軸旋轉SINS中軸向陀螺漂移進行了研究。Sun Wei[10]針對傳統單軸旋轉方案中軸向陀螺常值漂移無法被調制問題，提出一種旋轉軸傾斜45°的單軸旋轉方案，并進行了仿真和系統驗證實驗。于旭東[11]建立了軸向陀螺常值漂移與經緯度誤差數學模型，并利用最小二乘法辨識軸向陀螺常值漂移。胡杰[12]在文獻[11]的研究基礎上，針對經緯度誤差中的舒拉振蕩誤差對陀螺漂移辨識精度影響，提出利用水平阻尼網絡抑制舒拉振蕩誤差以精確估計軸向陀螺漂移。Gao Wei[13]、孫偉[14]建立了旋轉式SINS精對準Kalman濾波狀態方程和量測方程，在初始對準的同時對IMU誤差進行估計，仿真結果顯示IMU水平誤差、“數學平臺”失準角等誤差降低了軸向陀螺常值漂移估計精度。綜上文獻可知，目前最小二乘法和Kalman濾波法是單軸旋轉SINS中常用的兩種估計軸向陀螺常值漂移的方法，其中，最小二乘法耗時長且需要載體保持靜止狀態，而Kalman濾波法中其它狀態誤差會影響軸向陀螺常值漂移估計精度，為此需要結合SINS導航誤差模型，分析誤差傳遞特性，研究一種適用于單軸旋轉SINS的軸向陀螺常值漂移自標定方法。

本文首先對單軸旋轉SINS調制原理進行了分析，并給出了導航誤差模型，然后開展在線自標定數學模型研究，給出了在線自標定Kalman濾波狀態方程和量測方程，最后針對單軸旋轉SINS中軸向陀螺誤差傳遞特性，提出利用兩級Kalman濾波器實現IMU誤差的精確估計與補償。進行了計算機仿真和實際系統驗證實驗，結果表明本文所提出方法的正確性，能夠為中等精度單軸旋轉SINS的研制提供理論參考。

2 單軸旋轉SINS調制原理與誤差模型

2.1 旋轉調制原理

傳統SINS中，IMU安裝在固定支架上并且與載體固連，IMU誤差會引起位置隨時間積累性誤差，無法滿足高精度導航需求。單軸旋轉SINS中，IMU安裝在能夠繞軸向旋轉的內部平臺上，使得IMU(s系，oxsyszs)相對載體坐標系(b系，oxbybzb)旋轉，從而水平方向上IMU誤差呈周期性變化，通過積分予以抵消。

假設初始時刻s系與b系重合，系統通電后s系以角速度Ω繞方位軸旋轉，則在任意t時刻s系相對b系的夾角為Ωt，其方向余弦矩陣可表示為

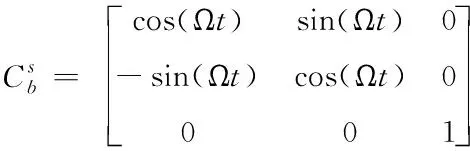
(1)

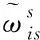
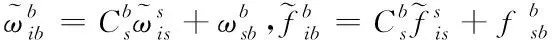
(2)

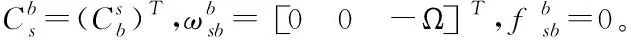
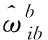
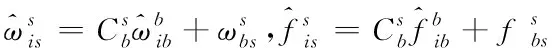
(3)

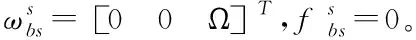
陀螺和加速計的測量值為

(4)

由式(2)、式(3)和式(4)可以得

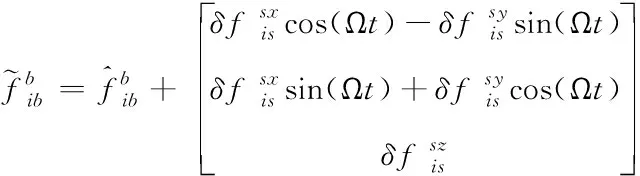
(5)

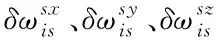
由式(5)可以看出，在單軸旋轉SINS中，當IMU繞方位軸旋轉時， IMU水平誤差在b系中呈周期性變化，通過積分可以抵消，IMU軸向誤差依然保持不變，因此對于單軸旋轉SINS而言，有必要采取其它措施對IMU軸向誤差進行估計與補償，以進一步提高SINS導航精度。

2.2 導航誤差模型

旋轉調制技術的本質是通過控制IMU做周期性的轉動以改變SINS姿態矩陣，使得短時間內IMU誤差對導航系統的積分等于零。旋轉式SINS導航算法與非旋轉時具有一致性，因此，可得旋轉式SINS導航誤差方程如下所示。

旋轉式SINS姿態誤差方程為

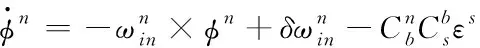
(6)

旋轉式SINS速度誤差方程為

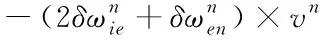
(7)

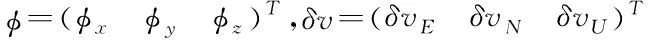
旋轉SINS位置誤差方程為

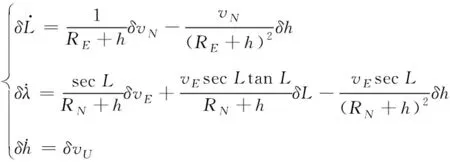
(8)

式中，δL、δλ和δh分別表示導航系統計算得載體緯度誤差、經度誤差和高度誤差，δvE、δvN、δvU分別東向、北向和天向速度誤差，RE和RN分別表示地球子午圈和卯酉圈的曲率半徑。

3 在線自標定數學模型

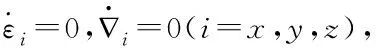
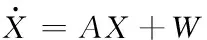
(9)

式中，A為系統狀態轉移矩陣，W為系統過程噪聲矢量，X為系統誤差狀態矢量，其表達式如式(5)所示

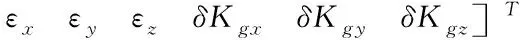
(10)

式中，?x、?y為沿著旋轉系水平方向上加速度計常值偏置，εx、εy、εz為沿著旋轉系三個方向陀螺常值漂移，δKgx、δKgy、δKgz為沿著旋轉系三個方向陀螺標度因數誤差。根據旋轉式SINS誤差方程式(6)～(8)可以得到精對準狀態轉移矩陣A為

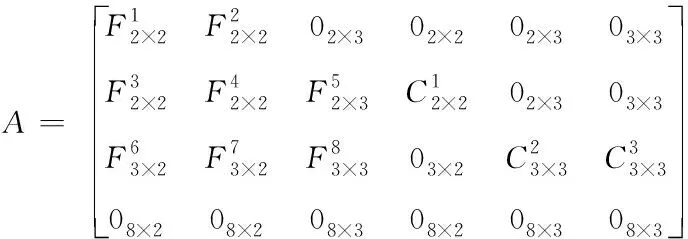
(11)

式中

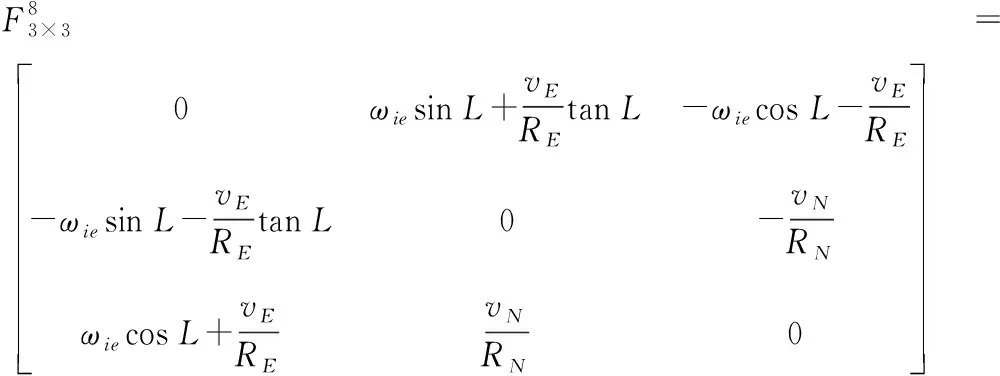
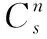
選取位置誤差δL、δλ和水平速度誤差δvE、δvN為觀測值，量測方程為

Z=HX+V

(12)

式中，Z為觀測向量，Z=[δLδλδvEδvN]T，V為系統量測噪聲矢量，H為量測矩陣，其表達式為

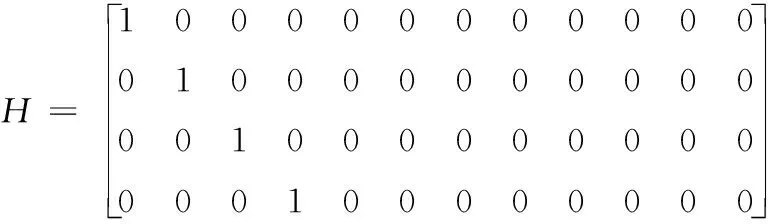
(13)

4 兩級Kalman濾波算法流程

單軸旋轉SINS中水平方向IMU誤差可觀測度高，而軸向IMU誤差可觀測度相對較低，為了提高軸向IMU誤差標定精度，需要對SINS誤差傳遞形式進行分析，圖1為與軸向陀螺常值漂移估計相關的主要誤差傳遞過程。

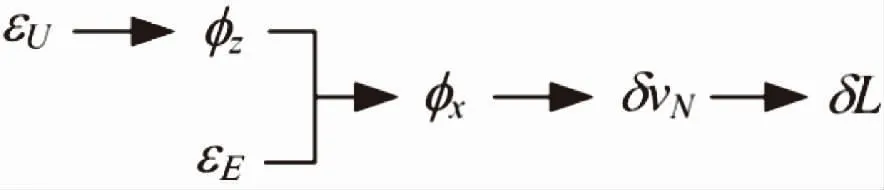
圖1 軸向陀螺常值漂移傳遞形式

圖1中，εE、εU分別表示等效東向、軸向陀螺常值漂移，δvN、δL分別表示SINS北向速度誤差和緯度誤差，φx、φz分別表示SINS“數學平臺”東向和天向失準角。由圖1可以看出，當Kalman濾波器利用速度或者位置誤差作為觀測量進行狀態最優估計時，等效東向陀螺常值漂移、方位失準角、等效北向加速度計偏置等都會影響濾波器軸向陀螺常值漂移估計精度，為此需要設計一個合理的自標定流程，以最大限度地減小這些誤差因素的影響。

針對單軸旋轉SINS中軸向陀螺常值漂移傳遞特性，為了實現其精確估計，設計了兩級Kalman濾波器，并在第二級Kalman濾波器中完成軸向陀螺常值漂移和標度因素誤差的精度估計，其自標定流程圖如圖2所示。

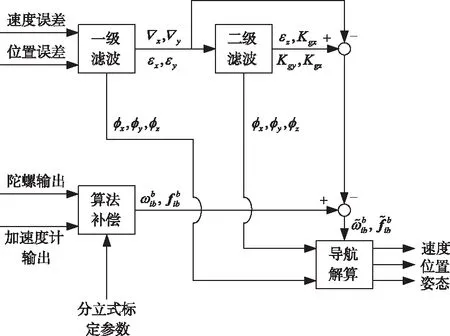
圖2 基于兩級Kalman濾波的自標定流程圖

由圖2可以看出，首先，第一級Kalman濾波器利用速度和位置基準信息估計數學平臺“失準角”以及水平方向陀螺常值漂移和加速度計常值偏置，并進行補償后作為第二級Kalman濾波器的輸入，然后，進一步利用基準速度和位置信息對軸向陀螺常值漂移以及陀螺標度因數誤差進行在線估計，從而完成系統自標定工作并轉入導航工作模式。

5 仿真與分析

5.1 仿真參數設置

假設陀螺常值漂移為0.01°/h，角度隨機游走系數為0.005°/h1/2，標度因數誤差為10ppm，安裝誤差均為5″；加速度計常值偏置為100μg，隨機游走系數為80μg·s1/2，標度因數誤差為10ppm，安裝誤差均為5″。初始經度106.69°，緯度26.51°；仿真系統模擬搖擺運動，姿態角變化規律分別為：俯仰角θ=5°sin(2πt/5)，橫搖角γ=2°sin(2πt/1.25)，航向角ψ=5°sin(2πt/5)，假設載體處于系泊狀態，線速度為0。

仿真中轉位機構采用四位置正反轉停旋轉方案，如圖3所示。旋轉機構角加速度為8°/s2，當角速度達到16°/s時保持轉位機構勻速旋轉運動，并在到達指定位置后以-8°/s2的加速度減速，直至最終角速度為0，其測角裝置誤差假設為5″。

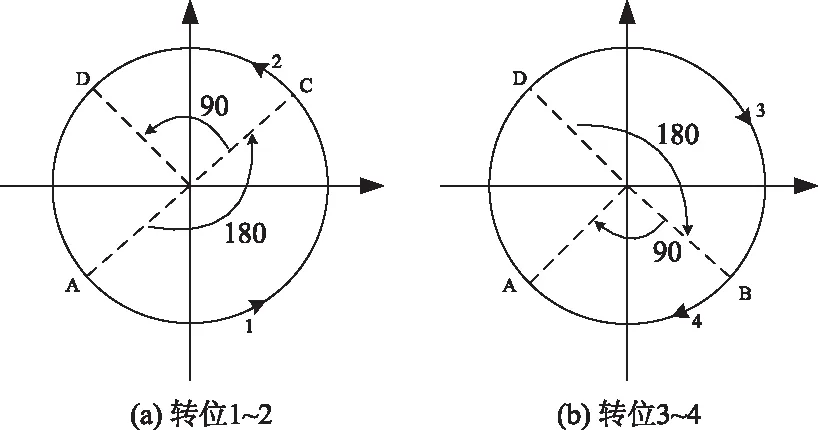
圖3 四位置旋轉方案

轉位1 IMU由A點逆時針轉動180°到達C點，然后停止5min；

轉位2 IMU由C點逆時針旋轉90°到達D點，然后停止5min；

轉位3 IMU由D點順時針旋轉180°到達B點，然后停止5min；

轉位4 IMU由B點順時針旋轉90°到達A點，然后停止5min；

然后以此順序進行循環運動。

5.2 實驗結果

單軸旋轉SINS啟動上電后即進行粗對準，粗對準時間為3min，假設系統粗對準后姿態角誤差為Δψ=0.5°，Δθ=Δγ=0.1°，隨后進行一級Kalman濾波估計，經過15min后可以得到較為精確的數學平臺“失準角”與IMU水平方向誤差并進行補償，隨后進行第二級Kalman濾波，對軸向陀螺常值漂移和陀螺標度因數誤差進行估計，持續時間為2h，標定結果如圖4～圖8所示，標定結果統計如表1～表4所示。

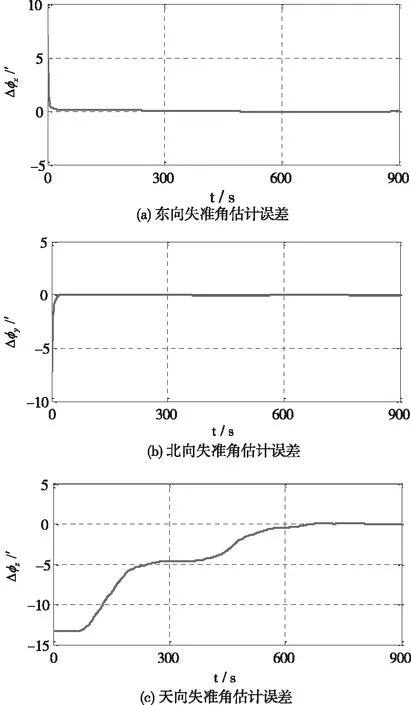
圖4 “數學平臺”失準角估計誤差曲線

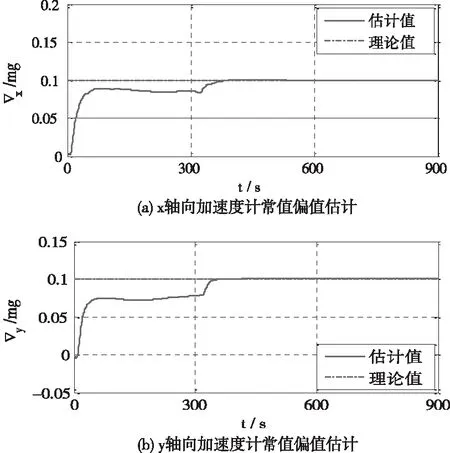
圖5 水平方向加速度計常值偏置估計曲線

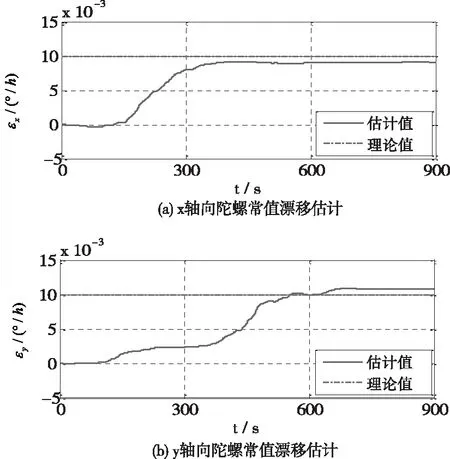
圖6 水平方向陀螺常值漂移估計曲線

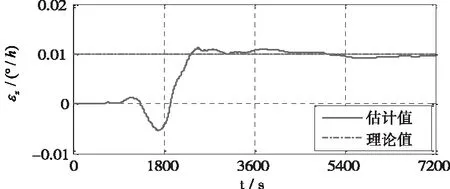
圖7 軸向陀螺常值漂移估計曲線

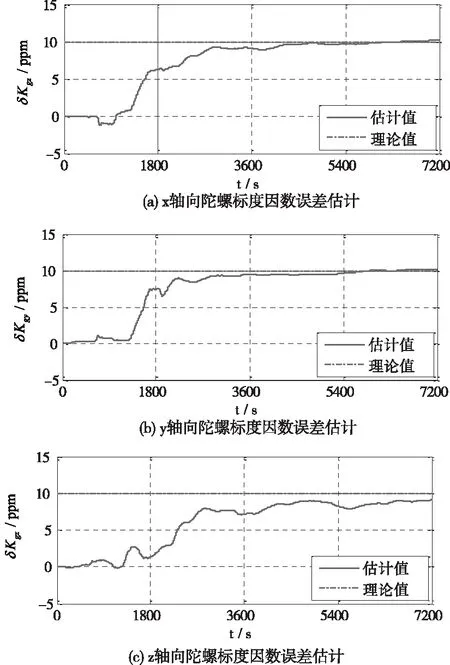
圖8 陀螺標度因數誤差誤差估計曲線

在單軸旋轉SINS中，周期性轉動IMU抵消了水平方向常值漂移誤差對失準角估計精度影響，由圖4和表1可以看出，三個方向失準角估計收斂精度高，特別是方位失準角收斂誤差為0.0021′，滿足高精度SINS對初始對準精度需求。同時，由圖5、圖6以及表2、表3可以看出，水平方向IMU誤差經過15min濾波估計后，最終能夠收斂至真值附近。

表1 失準角估計誤差

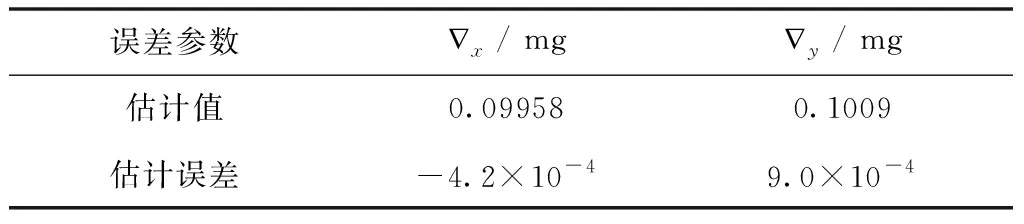
表2 加速度計常值偏置估計值

表3 陀螺常值漂移估計值

第一級Kalman濾波器完成初始失準角以及水平方向IMU誤差估計后轉至執行第二級Kalman濾波，開始對軸向陀螺常值漂移以及陀螺標度因數誤差進行估計，由于軸向陀螺常值漂移和陀螺標度因數誤差可觀測度相對較低，因此，其估計收斂時間較長，由圖7、圖8以及表3、表4可以看出，經過2h在線估計后，軸向陀螺常值漂移及其標度因數誤差得以精確估計，實現了單軸旋轉SINS在線自標定目的。

完成兩級Kalman濾波后進行24h純慣性導航仿真，對比有無標校實驗前后SINS長時間導航精度，結果如圖9所示。

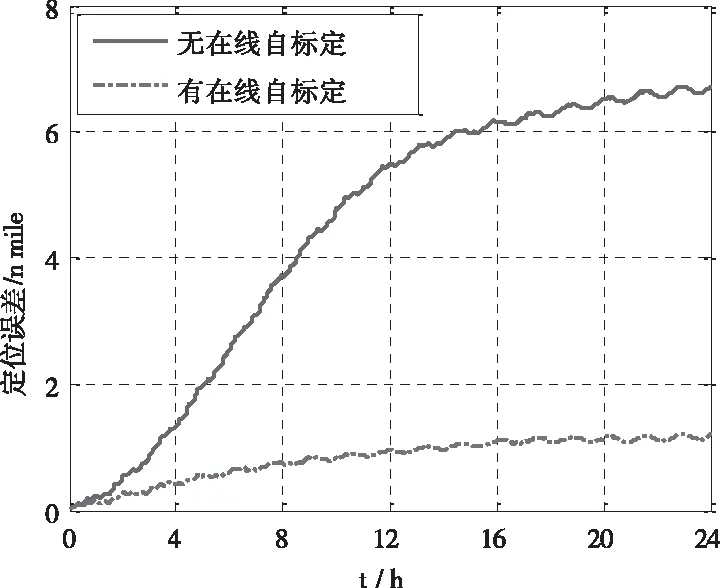
圖9 有無在線自標定SINS位置誤差對比

表5 不同實驗方案下的定位誤差

由圖9和表5可以看出，如果不進行IMU常值漂移誤差系統標校，捷聯慣導系統24h定位誤差為6.71n mile，通過在線系統級標校，主要是完成轉軸方向上陀螺漂移誤差的估計與補償，其后長時間定位僅有1.96n mile，相比無系統級標校，其定位精度得到提高。

6 系統驗證實驗

利用實驗室研制的單軸旋轉SINS進行初始對準驗證實驗，其中，IMU由3個光纖陀螺和3個石英撓性加速度計組成，其主要性能指標如表6所示。

表6 單軸旋轉SINS主要性能指標

單軸旋轉SINS以及三軸轉臺如圖10所示，將SINS放置在三軸轉臺上，控制轉臺做三軸搖擺運動，為了模擬水中兵器受海浪影響而產生的角運動，設置俯仰角搖擺幅度為5°，周期為5s，橫搖角搖擺幅度為2°，周期為1.25s，航向角搖擺幅度為5°，周期為5s，Kalman濾波器更新周期為1s。

圖10 實驗設備及環境

采用一組轉臺IMU實測數據進行半物理驗證實驗，圖11為有無在線自標定過程時SINS位置誤差對比曲線，圖中藍色曲線為無在線自標定過程時SINS導航12h時位置誤差曲線，紅色點畫線為有在線自標定過程時SINS導航12h位置誤差曲線。

圖11 有無在線自標定SINS位置誤差對比

表7 不同實驗方案下的定位誤差

由圖11和表7可以看出，實際導航系統中，對IMU誤差在線自標定提高了SINS長時間導航定位精度，其12h位置誤差由5.14n mile減小為2.13n mile，具有工程應用價值。

7 結束語

本文對單軸旋轉SINS軸向陀螺漂移在線自標定方法進行了研究。首先分析了旋轉調制原理，并給出了在線自標定Kalman濾波狀態方程和量測方程。然后對軸向陀螺漂移誤差傳遞路徑進行了分析，指出等效東向陀螺漂移、“數學平臺”失準角、等效北向加速度計偏置等會影響軸向陀螺常值漂移估計精度，為此提出了一種基于兩級Kalman濾波的單軸旋轉SINS軸向陀螺漂移自標校方法。最后進行了仿真和實際系統驗證實驗，可以看出，第二級Kalman濾波器能夠較好地實現軸向陀螺常值漂移和標度因數誤差的精確估計，同時轉臺驗證實驗中，單軸旋轉SINS經過在線自標定與補償后，其位置誤差減小了58.6%，由此驗證了本文所提出方法的正確性。