考慮火電深度調峰煤耗特性的隨機機組組合
劉 蕓,韓 松,黃秋立
(貴州大學電氣工程學院,貴州 貴陽 550025)
1 引言
深度調峰是指機組超過基本調峰范圍進行調峰的一種運行方式。近年來,隨著新能源接入電網比例的增加,電網負荷峰谷差逐漸增大,電力系統調峰問題日益突出,火電機組承擔深度調峰任務將成為常態。但風電等新能源出力具有隨機性、間歇性等特點,大規模風電并網給電力系統帶來了嚴峻的挑戰。因此,開展考慮火電機組深度調峰煤耗特性的隨機機組組合問題研究具有重要意義。
一方面,從火電機組深度調峰角度看,目前相關文獻中采用的煤耗模型大多基于火電機組基本調峰階段的煤耗特性,較少考慮火電機組參與深度調峰時煤耗特性的變化。實際運行中,機組負荷的變化將對機組煤耗率造成較大的影響,導致研究中采用的煤耗模型與實際情況存在較大的差異。文獻[1]在不同負荷下按機組的設計標準煤耗進行優化調度,與實際情況差別太大。文獻[2]建立了計及調峰主客體因素的深度補償模型,采用基于基本調峰階段的發電費用函數,無法反應機組深度調峰時煤耗特性的變化。文獻[3]提出計及機組壽命損耗和環境效益的火電機組不同階段的調峰能耗成本模型,但未考慮風電的隨機性對系統的影響。
另一方面,從風電隨機性的角度看。風功率預測包括風電功率點預測、區間預測和概率場景預測。文獻[4][5]采用點預測的方法,無法反應風電出力的隨機性,會給電力系統帶來較大的風險。文獻[6]采用置信區間法進行風電不確定性建模,相比概率場景方法,其代表性較差。文獻[7]采用蒙特卡洛抽樣法,其樣本可以落在輸入分布范圍內的任何位置,而拉丁超立方抽樣法(Latin Hypercube Sampling,LHS)通過對輸入概率分布進行分層抽樣,其樣本能更準確地反應輸入概率分布中值的分布。因此,本文從風電功率概率場景預測入手,采用LHS進行抽樣,通過后向場景削減技術降低模型的復雜度,對風電功率預測的不確定性進行描述。
為此,本文建立考慮深度調峰時火電機組煤耗特性的機組組合模型,并在模型中引入風電概率場景預測來表征風電出力的隨機性,利用Matpower Optimal Scheduling Tools (MOST)[8][9]對一個修改的IEEE 6機30節點系統進行算例分析,研究火電機組深度調峰時,不同火電機組煤耗模型對機組組合的影響。
2 火電機組深度調峰煤耗特性及成本表達
2.1 火電機組深度調峰煤耗特性
火電機組的煤耗特性是評估火電機組節能潛力、提高機組調峰運行經濟性的基礎。機組基本調峰階段煤耗率變化不大,但火電機組深度變負荷會導致機組和各個輔機的運行工況均會大幅度偏離設計值,供電煤耗率、廠用電率和汽輪機熱耗率等經濟性指標會大幅度降低[10]。變負荷過程中,隨著負荷降低,汽輪機機組絕對內效率下降速度變快,導致火電廠發電標準煤耗率將在低負荷運行時迅速升高。在低負荷時鍋爐燃燒狀況若發生惡化,將對鍋爐的屋里燃燒熱損失產生影響,進而影響鍋爐效率,使機組煤耗率進一步升高[11]。
不同容量和參數的火電機組發電標準煤耗率如圖1所示。隨著機組容量和參數增大,機組煤耗率減小;隨著負荷率的下降,火電機組煤耗率逐漸增加,并且增加的速度。
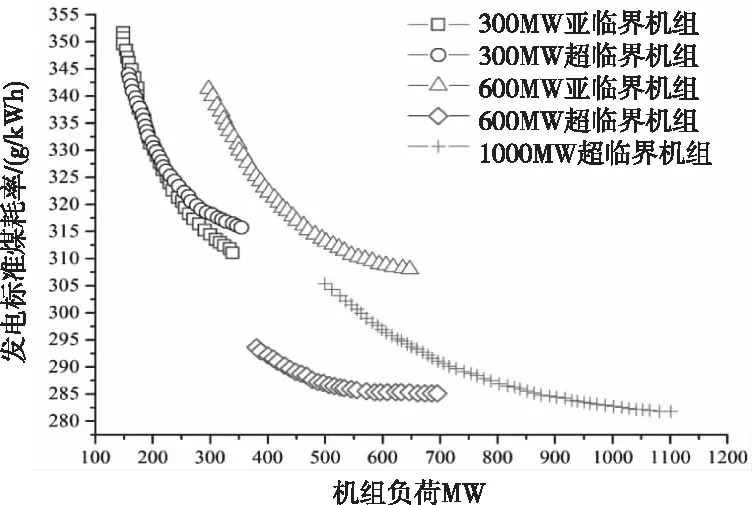
圖1 火電機組深度調峰煤耗特性
2.2 基于嚴格分段線性的煤耗成本表達
根據機組煤耗率曲線,利用最小二乘法擬合火電機組煤耗成本,得出煤耗成本函數的二次項系數為負,此時煤耗成本函數為非凸函數,求解存在困難。因此,需要對非凸火電煤耗成本函數進行線性化處理。

圖2 二次成本函數分段線性化
目前電力系統機組組合中廣泛應用的二次成本函數分段線性化方法是均分法,但采用均分法分段線性化成本函數進而計算得到的機組組合結果與直接采用原始二次成本方程求解得到的機組組合結果差別較大。為提高分段線性逼近原始二次成本函數的精度,本文通過最小化弧長和弦長平方差,對考慮火電機組深度調峰煤耗特性變化的二次煤耗成本函數進行準確地線性化[12]。

(1)
式中,ARCik為第k段的弧長,計算公式如式(2)所示;CHDik為第k段的弦長,計算公式如式(3)所示
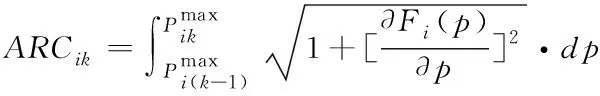
(2)
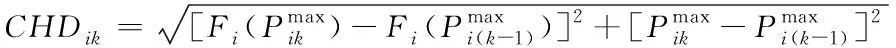
(3)

假設將機組i的二次成本曲線分成N段,原二次成本函數為
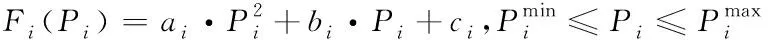
(4)

嚴格分段線性化后的方程為

(5)

(6)
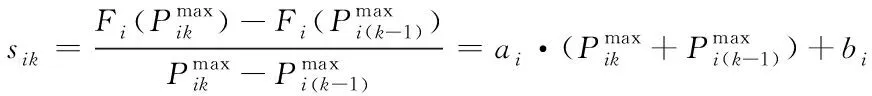
(7)

3 模型描述
3.1 基于場景分析的風電隨機性表達
首先,采用雙參數威布爾分布對風速歷史數據進行概率擬合。然后,利用LHS生成原始采樣矩陣,對N個采樣值進行威布爾分布逆變換得到風速場景集。由于風速場景數龐大使得模型求解困難,本文采取后向場景削減技術對N個風速場景進行削減,并考慮目標場景集的擬合精度,得到場景數為n的目標場景集。最后,利用風速-風功率轉換公式,得出典型風電出力場景集。
為保證機組組合的效率,本文采用文獻[13]中所提的差異度D作為場景削減精度的評判指標,D越小,代表場景擬合的精度越高。
3.2 目標函數
以火電機組運行成本最小為目標函數,火電機組運行成本包括煤耗成本和啟停成本,具體表示為

(8)
3.3 約束條件[8-9]
在任意時刻,為保證系統安全穩定運行,都必須要滿足以下約束條件。
1) 常規最優潮流約束
系統功率平衡約束
gtij(θtij,Vtij,ptij,qtij)=0
(9)
線路容量、電壓等最優潮流約束
htij(θtij,Vtij,ptij,qtij)≤0
(10)
式中:gtij(·)為t時刻場景j下的非線性交流潮流方程;htij(·)為t時刻場景j下的傳輸線、電壓和其它約束;θtij、Vtij、ptij、qtij分別為t時刻場景j下的電壓相角、電壓幅值、機組i的有功出力和無功出力。
2) 備用容量約束

(11)

(12)

3) 爬坡約束

(13)
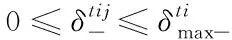
(14)
4) 機組組合約束

(15)

(16)
uti-u(t-1)i=vti-wti
(17)
0≤vti≤1
(18)
0≤wti≤1
(19)

(20)
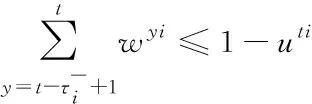
(21)
uti∈{0,1}
(22)

3.4 求解方法
本文所提隨機機組組合模型求解流程圖如圖3所示。首先,借助一種非均分嚴格分段線性逼近方法,對考慮火電機組深度調峰煤耗特性的二次煤耗成本函數進行線性化。此外,考慮風電出力的隨機性,采用LHS生成風電出力場景集,綜合考慮模型計算效率和精度,利用后向場景削減技術降低模型的復雜度,再通過風速-風功率轉換公式獲得典型風電出力場景集。
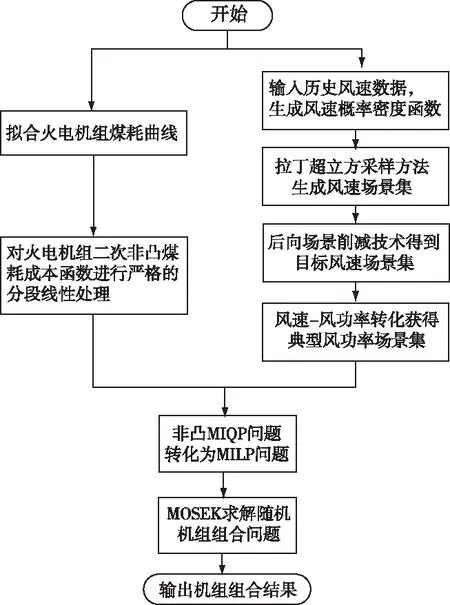
圖3 本文所提隨機機組組合模型求解流程圖
綜上所述,將非凸混合整數二次規劃問題(MIQP)轉換為混合整數線性規劃問題(MILP),采用MOSEK[14]對機組組合模型進行求解。
4 算例分析
4.1 算例系統
本文采用了一個修改的IEEE 6機30節點系統[15]進行仿真分析。算例系統如圖4所示,節點2為風電場并網點,火電機組參數見表1。設置機組組合時間范圍為14天(336小時),時間間隔取1h。負荷數據見圖5。以美國NERL風速數據為例進行風速概率分布建模,選取2019年3月6日-3月19日80m高、采樣間隔為1h的實測風速。設置切入速度為3.5m/s,額定風速為12.5m/s,切出風速為25m/s。風電場額定輸出功率為100MW。

圖4 算例系統
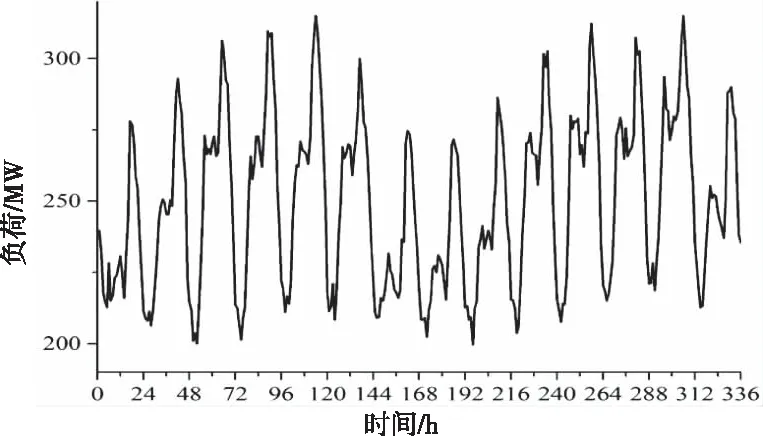
圖5 負荷曲線
火電機組深度調峰運行的煤耗特性參見文獻[16]。設置火電機組基本調峰時煤耗率等于煤耗率曲線上負荷最大時的發電標準煤耗率。

表1 火電機組參數
4.2 不同煤耗模型對機組組合的影響
將本文所提機組組合模型(即模型1)與只考慮火電機組基本調峰煤耗特性的機組組合模型(即模型2)進行對比。選取機組1、機組2為調峰機組,調峰深度為70%,其余機組基本調峰,調峰深度為40%。依據圖3流程圖求解不同煤耗模型下的機組組合,煤耗情況見表2,兩種模型下機組組合結果見圖6和圖7。

表2 不同模型煤耗情況
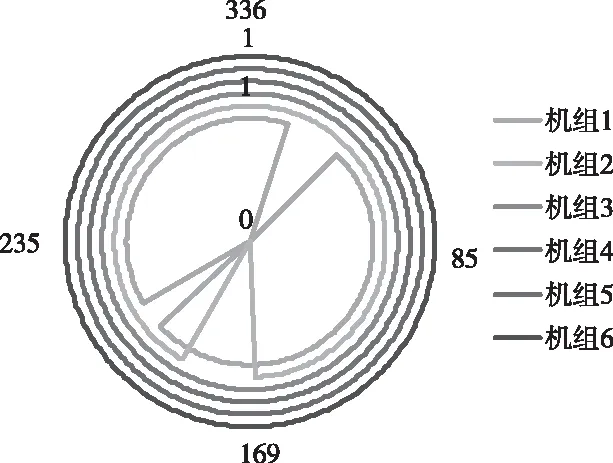
圖6 模型1機組組合結果
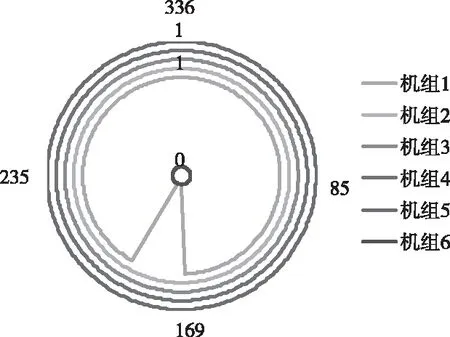
圖7 模型2機組組合結果
由表2可以看出,采用模型1時系統煤耗量和煤耗成本均高于模型2,這主要是由于火電機組參與深度調峰的實際機組煤耗率高于基本調峰時的煤耗率。兩種模型下系統煤耗情況相差不大,驗證了本文所提模型的有效性。
比較圖6和圖7可以看出,兩種模型下機組組合不同,采用模型1時機組啟停機次數更多。這主要是由于采用模型1時機組煤耗率高于模型2,為降低煤耗成本,采用模型1時調峰機組出力在在較長時間內小于模型2,為滿足負荷需求,機組6投入運行,進而導致兩種模型下機組組合不同。這表明兩種模型的區別是不容忽視的。由不同模型下的機組出力可以看出,采用模型1時,深度調峰機組參與調峰次數明顯增加。可見,計及火電機組深度調峰煤耗特性,火電機組會更多地參與深度調峰。
4.3 不同調峰深度對機組組合的影響
選取調峰深度分別為40%,50%,60%和70%,依據圖3流程圖求解不同調峰深度下的機組組合模型,煤耗成本見圖8。
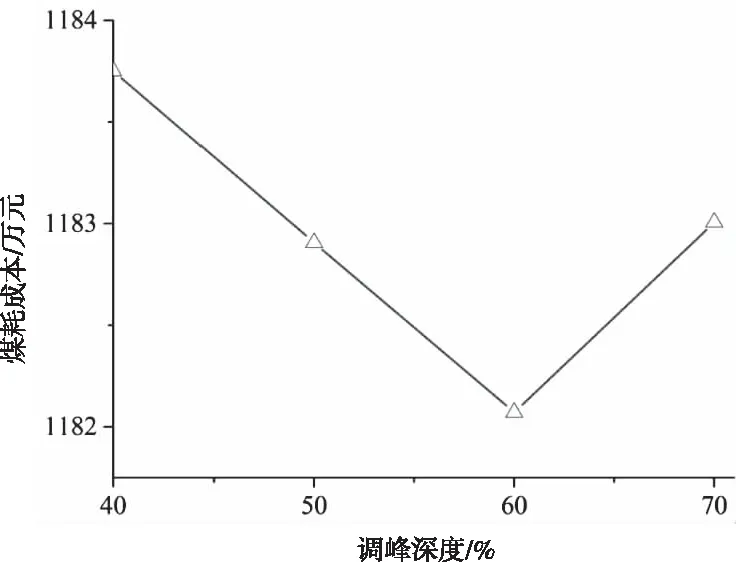
圖8 不同調峰深度下的煤耗成本
由不同調峰深度下的機組組合可知,調峰機組的調峰深度為40%時,機組6在不出力的情況下,其余機組也能滿足負荷需求。當調峰機組的調峰深度繼續增加時,機組啟停情況出現變化,隨調峰深度的增加,調峰機組啟停次數減少,并且機組2的停機時刻推遲,停機時間也在縮短。這表明提高火電機組的調峰深度后,調峰機組可長時間進入深度調峰狀態,調節作用明顯。
由圖8可以看出,考慮火電機組深度調峰煤耗特性時,系統煤耗成本并非隨調峰深度增加而單調降低。當調峰機組的調峰深度小于60%時,系統煤耗成本隨機組調峰深度增加而降低;當調峰機組的調峰深度大于60%時,煤耗成本反而隨調峰深度的增加而升高。可見,對本算例來說,應合理設置火電機組調峰深度以獲得更好的經濟效益。
4.4 不同風電接入容量對機組組合的影響
風電并網容量的增大會導致風電出力隨機性增強,分析不同風電接入容量對系統的影響,依據圖3求解流程圖求解不同風電接入容量下的機組組合模型,煤耗成本見圖9。

圖9 不同風電接入容量下煤耗成本
由不同風電接入容量時的機組組合可知,隨著風電接入容量的提高,調峰機組啟停次數明顯增加。這是由于風電接入容量的增大使風電出力隨機性增強,給系統帶來較大的波動性,進而使得機組狀態發生變化。
由圖9可見,隨著風電接入容量的增加,兩種模型下的煤耗成本均呈下降趨勢,說明風電接入能減少火電機組的燃煤費用。然而,對調峰機組來說,煤耗成本并未隨風電接入容量的增加而降低。機組1在風電接入容量為90MW時的煤耗成本比風電接入容量為60MW時高7.95萬元。可見,對調峰機組來說,并不是風電接入系統容量越大,機組經濟效益越好。
5 結論
為準確分析含高比例間歇性新能源的電力系統機組組合問題,本文提出了一種考慮火電機組深度調峰煤耗特性的隨機機組組合模型。一個修改的IEEE 6機30節點系統的336小時機組組合算例計算結果表明了該模型的有效性。此外,有以下幾點發現和認識:
1)火力機組深度調峰時煤耗特性呈現一定的非凸特性,相關機組占比大時,將對機組組合、機組參與深度調峰情況產生較大影響。
2)系統調峰能力隨調峰機組調峰深度的增加而增強。部分機組參與深度調峰可以獲得更好地經濟效益,但火電機組煤耗成本并不一定隨調峰深度的增加而單調增加。
3)高比例間歇性能源會給系統帶來較大的隨機性。風電大規模接入能夠降低系統煤耗成本,但對深度調峰機組來說,其煤耗成本并非隨風電接入容量增加而單調降低。

