滾動時域下最小加工時間批調(diào)度與粒子群求解

王宗光，謝小青，楊玉龍，廖世龍*

(1.蘭州理工大學(xué)經(jīng)濟管理學(xué)院，甘肅 蘭州 730050； 2.山東大學(xué)管理學(xué)院，山東 濟南 250100)

1 引言

批調(diào)度問題主要指工件排序及工件合批，是半導(dǎo)體生產(chǎn)過程中提煉出的新型調(diào)度問題[1]。合批根據(jù)批處理設(shè)備的容量、工件形狀材質(zhì)、工件到達(dá)時間以及加工成本等多種因素綜合處理。因此，批調(diào)度在求解難度上遠(yuǎn)高于古典調(diào)度[2]。實踐生產(chǎn)中，批調(diào)度以適當(dāng)?shù)臅r間周期或事件驅(qū)動進行循環(huán)調(diào)度，僅需考慮怎樣對某一時段內(nèi)的工件分批、排程[3]，將動態(tài)、長期的全局調(diào)度問題分解為各時段內(nèi)靜態(tài)的局部子調(diào)度問題。傳統(tǒng)批調(diào)度在各調(diào)度周期內(nèi)只使用一種方法和一種確定的規(guī)則來解決問題，以便于調(diào)度的實現(xiàn)。而滾動時域調(diào)度方法則是時間驅(qū)動的循環(huán)調(diào)度策略。

當(dāng)前批調(diào)度的研究可分為兩種：一是理論。Liu的研究表明即便單臺機器的工件集只有兩個到達(dá)時間，批調(diào)度問題也是NP難題[4]。Zhao證明了目標(biāo)為拖期懲罰的連續(xù)型批調(diào)度問題為強NP難[5]。二是算法，研究主要集中于初始時刻全局信息完全時，利用常規(guī)算法或群智能優(yōu)化算法等離線算法進行一次的全局靜態(tài)調(diào)度，獲得調(diào)度最優(yōu)值[6-8]。Melouks和Damodaran分別采用模擬退火算法、遺傳算法對制造跨度進行優(yōu)化研究[9，10]。Tang和Song設(shè)計了離散粒子群算法并將其應(yīng)用在鋼輥熱處理混合流水車間[11]。閆萍和袁媛以化工領(lǐng)域設(shè)備批處理過程為研究對象，構(gòu)建了分批與批調(diào)度決策的優(yōu)化模型并提出改進的DE算法，仿真得出與PSO算法相比，改進的DE算法性能更好[12]。

實際生產(chǎn)加工中，工件動態(tài)到達(dá)處理設(shè)備，對工件信息了解有限。Ovacik和Marcos較早的將滾動調(diào)度方法應(yīng)用到經(jīng)典調(diào)度問題中并取得了較好的效果[13，14]。但是，滾動時域調(diào)度策略下，各調(diào)度周期內(nèi)只進行局部調(diào)度且很難考慮全局信息，因此，無法對全局調(diào)度性能指標(biāo)作估計和控制[15]。Nelson和Sourirajan將滾動調(diào)度策略和實時狀態(tài)信息結(jié)合起來，首先把動態(tài)調(diào)度過程細(xì)分為多個連續(xù)靜態(tài)調(diào)度，再在每個區(qū)間內(nèi)逐個優(yōu)化，最后達(dá)到局部最優(yōu)[16，17]，進一步適應(yīng)動態(tài)生產(chǎn)環(huán)境的不斷變化，該研究表明滾動調(diào)度策略在解決調(diào)度問題上極具適用性[18]。

針對工件動態(tài)到達(dá)且調(diào)度開始時刻工件信息不完全的批調(diào)度問題，在時域內(nèi)利用粒子群算法進行調(diào)度優(yōu)化尋求局部調(diào)度最優(yōu)，并加入懲罰函數(shù)，確保局部調(diào)度目標(biāo)與全局目標(biāo)一致。對滾動時域策略下各調(diào)度規(guī)則下的調(diào)度結(jié)果進行了仿真，并對此類動態(tài)調(diào)度問題中不同參數(shù)取值下的仿真結(jié)果進行了討論。

2 滾動時域策略下批調(diào)度數(shù)學(xué)建模

2.1 滾動時域批調(diào)度問題描述

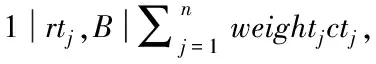
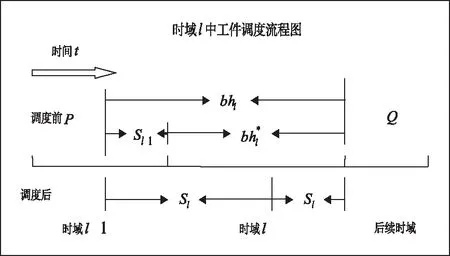
圖1 時域l中工件調(diào)度流程圖

2.2 符號說明

參數(shù)符號：

T：調(diào)度時域周期長度；

B：批處理設(shè)備的容量；

j：工件集合，其中j={1，2，…，n}；

rtj：工件j的到達(dá)時間；

ptj：工件j的加工時間；

sj：工件j的尺寸；

weightj：工件j的權(quán)重參數(shù)；

決策變量符號：

l：調(diào)度時域個數(shù)集，其中l(wèi)∈{1，2，…，L}，L為調(diào)度時域個數(shù)的最大值；

ctj：工件j的完工時間；

bhl：時域l內(nèi)待加工工件集；

bkl：調(diào)度時域l下的第k(k=1，2，…，Kl)批工件集；

RTkl：批bkl的到達(dá)時間；

STkl：批bkl的開始時間；

PTkl：批bkl的加工時間；

CTkl：批bkl的完工時間；

CTl：時域l中最后一批工件的完工時間；

Sl：時域l內(nèi)得到加工的工件集；

S′l：時域l內(nèi)未得到加工的工件集。

2.3 模型假設(shè)

1) 工件集合j={1，2，…，n}，每個工件包含如下信息：rtj、ptj、sj和weightj；

2) 批設(shè)備容量為B，是各時域中各批次的工件尺寸之和的最大值。批加工一旦開始，不能中斷，也不能放入新工件；

3) 以批次進行加工，批bkl的到達(dá)時間RTkl為批中所有工件的最大到達(dá)時間、加工時間PTkl為批中工件最大加工時間、開始加工時間計算方法：

當(dāng)k=1時

ST1l=max{RT1l，CTl-1，(l-1)T}

(1)

當(dāng)k=2，3，…，Kl時

STkl=max{RTkl，CT(k-1)l}

(2)

從而，批bkl的完工時間CTkl為

CTkl=STkl+PTkl

(3)

4) 調(diào)度時域l的周期為T。上一時域的結(jié)束時間即為下一時域的開始時間，某一時域的結(jié)束時間為該時域內(nèi)最后一個批次的完工時間。

2.4 滾動時域批調(diào)度數(shù)學(xué)模型

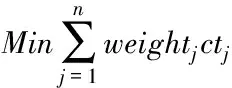
(4)

st.Yjkl={0，1}

(5)

(6)

(7)

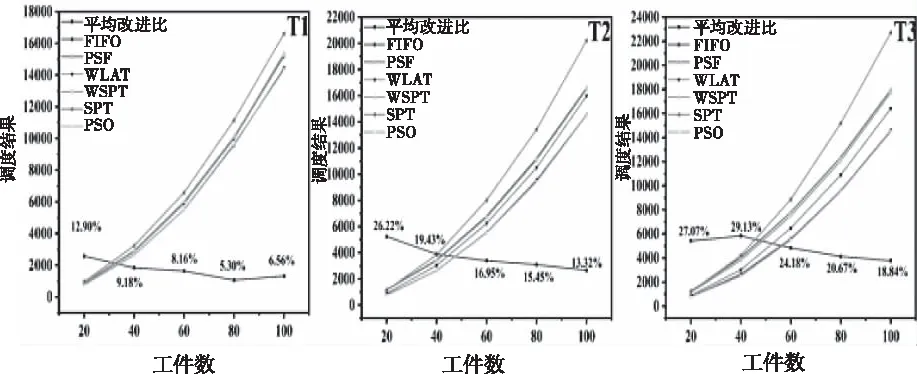
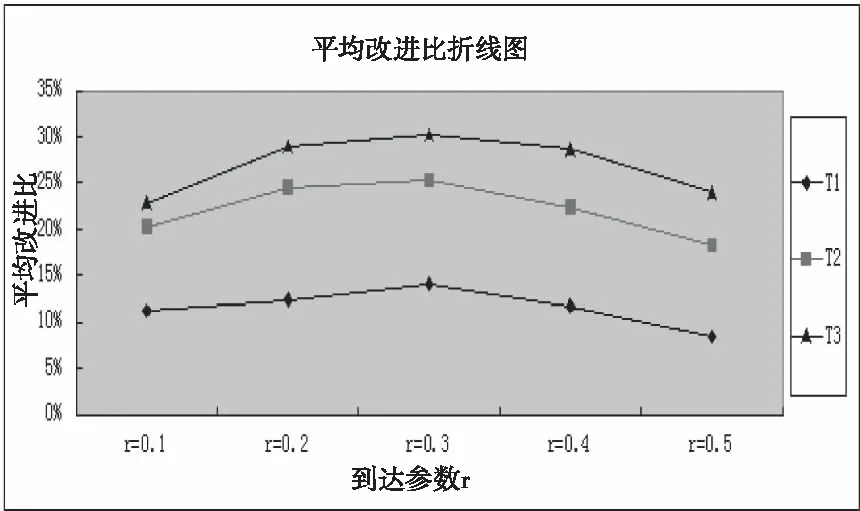
Sl={j|j∈bhl，stj

(8)

S′l={j|j∈bhl，stj≥l*T}

(9)

(10)

(11)

其中j={1，2，…，n}，k={1，2，…，Kl}，l={1，2，…，L}。式(4)是目標(biāo)函數(shù)，表示最小加權(quán)完工時間和；式(5)中，Yjkl為{0，1}決策變量，當(dāng)工件j屬于時域l中第k批時，Yjkl=1，否則，Yjkl=0；式(6)用以確保所有工件都能得到分批且工件不會重復(fù)加工；式(7)是工件分批的主要約束條件，表示同一批次內(nèi)所有工件的尺寸和應(yīng)當(dāng)不超過批設(shè)備容量；式(8)表示時域l中已加工的工件集；式(9)表示時域l中還沒有加工的工件集；式(10)表示時域l中加工工件數(shù)；式(11)表示時域l內(nèi)工件分批數(shù)量。

3 滾動時域批調(diào)度PSO算法實現(xiàn)

3.1 模型的初始化

第一個時域中待加工工件集為到達(dá)時間在周期內(nèi)的所有工件集合，后續(xù)時域中待加工工件集的確定方法參照圖1。假設(shè)時域l中，待加工工件數(shù)為n(l)，PSO算法的粒子數(shù)為N，各粒子用n(l)維向量表示。粒子i的位置向量Xi=(xi1，xi2，…，xin(l))，各Xi都表示一個工件序列。xij(j∈{1，2，…，n(l)})是粒子i中工件j的優(yōu)先值(xij越小，越靠前加工)，隨速度向量Vi=(vi1，vi2，…，vin(l))中vij的變化而變化。

3.2 PSO算法中工件排序、分批

時域l中，以先到先加工的規(guī)則進行工件初始調(diào)度，bhl按rtj從小到大依次排序。若rtj相同，ptj越小，工件排序越靠前。得到時域l內(nèi)工件調(diào)度的初始排序πl(wèi)，πl(wèi)(i)表示πl(wèi)的第i個工件。令第1個工件優(yōu)先值為πl(wèi)(1)=rand(0，1)，其它工件優(yōu)先值為[19]

πl(wèi)(i+1)=πl(wèi)(i)+rand(0，1)

(12)

將待加工工件先在批設(shè)備容量B的約束條件下分批，再計算當(dāng)前時域中微粒的適應(yīng)值。其中，活批是工件合批過程中，若至少存在一個批bk，在將工件j放入批bk后，仍然容量約束條件，則稱批bk為j的活批。否則，批bk為確定批。

為保證調(diào)度目標(biāo)，決策人員不會為了盡可能填滿批設(shè)備而無限制的等待滿足容量約束的工件到達(dá)。對于活批bk，在批等待時間內(nèi)到達(dá)的所有工件都可以合入成為同一批。分批規(guī)則：對于工件j有兩種安排方式，一是若當(dāng)前不存在批，或不存在對于j的活批，則j生成新的批，此時新的批為活批；二是若存在對于j的活批bk，當(dāng)j的到達(dá)時間與活批bk的到達(dá)時間間隔大于批等待時間，j進入新批，此時活批bk為確定批；否則，bk仍為活批。

4 局部懲罰函數(shù)與算法流程

4.1 局部調(diào)度懲罰函數(shù)

滾動時域調(diào)度下，①各調(diào)度時域結(jié)束時，部分工件已完成加工，后續(xù)時域中全局調(diào)度的自由度減小；②各調(diào)度時域下只加工部分工件，全局信息少。因此，時域l中目標(biāo)懲罰函數(shù)Δfl表示為

(13)

(14)

4.2 批調(diào)度算法流程

Step1：給出初始時刻信息不完全的n個工件集合S；

Step2：根據(jù)工件到達(dá)時間確定第一個時域l內(nèi)待加工工件集合bhl，該時域內(nèi)工件信息已知；

Step5：返回局部最優(yōu)調(diào)度適應(yīng)值fl，可得工件排序和分批，進而求得時域l內(nèi)的最優(yōu)目標(biāo)值Fl以及時域l內(nèi)得到處理的工件集Sl和未得到處理的工件集S′l；

Step6：令Tabu={j|j∈S-Sl}，若Tabu不為空集，將時域l內(nèi)未熱處理的工件集合S′l滾動進入l+1時域，與step2中的bhl+1合并，即bhl+1=S′l∪bhl+1，進入step3；若為空集，結(jié)束。

5 仿真研究

5.1 仿真參數(shù)設(shè)計與算法有效性分析

5.1.1 仿真參數(shù)設(shè)計

本文采用Melouks等提出的隨機產(chǎn)生數(shù)據(jù)的方法獲得算例[20]，算例劃分標(biāo)準(zhǔn)如下：

1)工件個數(shù)n分為J1、J2、J3、J4、J5類問題，工件數(shù)分別為20、40、60、80、100；

2)工件加工時間ptj服從[1，20]離散均勻分布；

3)工件尺寸sj服從[1，10]上的離散均勻分布；

4)工件到達(dá)時間rtj服從[0，rnE[ptj]]的離散均勻分布，其中r={0.1，0.2，0.3，0.4，0.5}，對應(yīng)于r1、r2、r3、r4、r5類問題，其工件到達(dá)時間間隔分別為1、2、3、4、5；

在批處理設(shè)備的容量B=30，PSO算法中粒子個數(shù)m=80，迭代次數(shù)NC_max=80的參數(shù)下，所有算例運行100次，利用Matlab2011b實現(xiàn)。由于算例中數(shù)據(jù)均為隨機產(chǎn)生，為防止個別極值的出現(xiàn)對運行結(jié)果產(chǎn)生影響，最終結(jié)果以除去10個最小值和10個最大之后的其余數(shù)值的平均值表示。文中不討論工件尺寸sj、加工時間ptj，得到不同到達(dá)時間下調(diào)度時域周期長度T分別為50、100、150時不同工件數(shù)的加權(quán)完成時間和。

對五種常規(guī)調(diào)度介紹如下，后續(xù)對五種常規(guī)調(diào)度的調(diào)度結(jié)果與PSO算法下批調(diào)度模型優(yōu)化后的調(diào)度結(jié)果進行比較。

1)先到先加工(FIFO)規(guī)則，調(diào)度時域內(nèi)工件按到達(dá)時間rt非降生成排序，常用于調(diào)度車間的一般調(diào)度問題中；

2)基于優(yōu)先權(quán)優(yōu)先(PSF)規(guī)則，調(diào)度時域內(nèi)工件按其權(quán)重weight非增生成排序，常用于工件含權(quán)重參數(shù)的批調(diào)度問題，但此調(diào)度規(guī)則容易造成熱處理爐等批處理設(shè)備的空閑時間；

3)加權(quán)最小到達(dá)時間優(yōu)先(WLAT)規(guī)則，調(diào)度時域內(nèi)工件按其重要度與到達(dá)時間的比值weight/rt非增生成排序，是FIFO規(guī)則和PSF規(guī)則的折中，不會導(dǎo)致熱處理爐產(chǎn)生大量的空閑等待時間；

4)加權(quán)最短加工時間優(yōu)先(WSPT)規(guī)則，調(diào)度時域內(nèi)工件按重要度與加工時間的比值weight/pt非增生成排序，在解決目標(biāo)為加權(quán)完工時間和靜態(tài)全局調(diào)度的問題中效果最佳；

5)最短加工時間優(yōu)先(SPT)規(guī)則，能在解決大規(guī)模工件的靜態(tài)調(diào)度問題中實現(xiàn)出很好的優(yōu)化性能。

5.1.2 基于PSO算法的滾動時域批調(diào)度模型的有效性與適用性分析

圖2中為r=0.1時的調(diào)度結(jié)果。首先，在不同工件數(shù)和調(diào)度周期下，基于PSO算法的滾動時域調(diào)度模型相對于其它五種常規(guī)調(diào)度規(guī)則的平均改進比最大值為24.99%，最小值為7.15%，體現(xiàn)了PSO算法對滾動時域策略下的批調(diào)度模型有較強的適用性；其次，調(diào)度周期T為50，SPT規(guī)則效果最佳；調(diào)度周期T為100、150時，WALT規(guī)則效果最佳。在相同工件數(shù)的情況下，隨調(diào)度周期的增加，由于SPT規(guī)則未考慮工件權(quán)重信息，調(diào)度結(jié)果也隨之增大。但調(diào)度周期的長短對FIFO、PSF、WLAT、WSPT四種規(guī)則的調(diào)度結(jié)果影響較小。工件密集到達(dá)，按照WLAT規(guī)則排序后不僅可保證較大權(quán)重的工件及早加工，而且批的開始加工時間較小。因此，WLAT規(guī)則在處理密集到達(dá)工件的調(diào)度時有較大優(yōu)勢。

圖2 r=0.1時調(diào)度結(jié)果 圖3 r=0.2時調(diào)度結(jié)果

圖3為r=0.2時的調(diào)度結(jié)果。PSO算法下調(diào)度結(jié)果的平均改進比值在7.9%到31.78%間，F(xiàn)IFO規(guī)則明顯優(yōu)于WSPT規(guī)則，但WLAT規(guī)則效果仍是最好的。此外，隨著調(diào)度周期變大，SPT、WSPT和PSF規(guī)則的調(diào)度結(jié)果也逐漸增大。

圖4和圖5分別為r=0.3、r=0.4時的調(diào)度結(jié)果。滾動時域批調(diào)度模型中PSO算法相對于常規(guī)調(diào)度規(guī)則的平均改進仍然可觀。在所有算例中，五種簡單調(diào)度規(guī)則中FIFO規(guī)則的調(diào)度優(yōu)化效果相對最優(yōu)，其次為WLAT規(guī)則，再次之為WSPT規(guī)則，PSF和SPT規(guī)則調(diào)度效果最差。相同工件數(shù)的算例中，除FIFO規(guī)則外，其它四種調(diào)度規(guī)則都是隨時域周期的增大，調(diào)度結(jié)果增大。

圖4 r=0.3時調(diào)度結(jié)果 圖5 r=0.4時調(diào)度結(jié)果

圖6 r=0.5時調(diào)度結(jié)果

圖6為r=0.5時的調(diào)度結(jié)果。此時，與其它常規(guī)調(diào)度規(guī)則相比，F(xiàn)IFO規(guī)則仍表現(xiàn)出極好的性能，但PSO算法調(diào)度結(jié)果在各調(diào)度周期下相對于FIFO規(guī)則的優(yōu)化效果則不明顯。說明了PSO算法在處理工件分散到達(dá)的情況下優(yōu)化效果不盡理想。導(dǎo)致這一現(xiàn)象的原因主要有兩點：①工件到達(dá)時間間隔較長，各調(diào)度時域內(nèi)到達(dá)的工件數(shù)量少，導(dǎo)致調(diào)度時域內(nèi)待調(diào)度工件數(shù)量也較少，PSO算法的優(yōu)化迭代性能得不到體現(xiàn)；②工件到達(dá)較為分散，導(dǎo)致整個調(diào)度過程產(chǎn)生較多的調(diào)度周期。盡管PSO算法調(diào)度過程中，各時域內(nèi)都設(shè)定了懲罰函數(shù)以確保局部調(diào)度目標(biāo)與全局目標(biāo)相一致，但過多的局部調(diào)度仍然會對全局目標(biāo)產(chǎn)生不小的影響。

綜合圖2到圖6以及圖7，可知：

1)除了在r=0.1，調(diào)度周期為T1、工件數(shù)分別為80和100的兩個算例，PSO算法下批調(diào)度模型優(yōu)化后的調(diào)度結(jié)果均優(yōu)于常規(guī)調(diào)度規(guī)則，說明基于PSO算法的滾動時域批調(diào)度模型具有很好的調(diào)度優(yōu)化效果。這兩個算例中SPT規(guī)則較優(yōu)的原因是由于工件到達(dá)時間間隔較短，且每個時域內(nèi)需加工的批數(shù)又相對較少，造成工件在批處理車間的阻塞，導(dǎo)致在每個調(diào)度周期的決策時刻，可供調(diào)度的工件數(shù)目較多。此時，按照工件加工時間排序還會使得絕大部分時域內(nèi)調(diào)度批數(shù)的增加，因而SPT規(guī)則的調(diào)度結(jié)果較理想。

2)FIFO、PSF、WLAT、WSPT、SPT五種常規(guī)調(diào)度規(guī)則中，隨著工件到達(dá)時間的增加，F(xiàn)IFO規(guī)則的調(diào)度優(yōu)化效果逐漸優(yōu)于WLAT規(guī)則的調(diào)度效果，且調(diào)度周期的長短對FIFO規(guī)則影響較小，從而間接證明了FIFO規(guī)則在實際調(diào)度中作為最常用的調(diào)度規(guī)則有獨有優(yōu)勢。

3)附錄中的圖5中，三條折線均為先升后降的走勢，說明隨到達(dá)時間參數(shù)r取值的增大，即工件到達(dá)由密集到分散時， PSO算法下滾動時域批調(diào)度模型的調(diào)度優(yōu)化性能先上升后下降。其次，由折線的不同高度可知，隨調(diào)度周期T的增大，模型及PSO算法的調(diào)度優(yōu)化效果增強。這表明，PSO算法下滾動時域批調(diào)度模型在解決調(diào)度周期長的批調(diào)度問題中效果更佳，優(yōu)勢明顯。

圖7 到達(dá)參數(shù)、時域周期與平均改進比折線圖

綜上，當(dāng)?shù)竭_(dá)參數(shù)固定后，在調(diào)度周期較長(即T越大)的批調(diào)度問題中， PSO算法下滾動時域批調(diào)度模型的效果越好。考慮極限的情況，即當(dāng)T→∞時，PSO算法可達(dá)到最優(yōu)調(diào)度，此時的批調(diào)度策略為一次的全局靜態(tài)調(diào)度，調(diào)度結(jié)果為滾動時域批調(diào)度問題的下界；當(dāng)T→0時，PSO算法優(yōu)化效果差，此時批調(diào)度方法為實時在線調(diào)度，調(diào)度結(jié)果為滾動時域批調(diào)度問題的上界。

6 結(jié)束語

設(shè)計了滾動時域調(diào)度策略，加入目標(biāo)懲罰函數(shù)，得出PSO算法下各調(diào)度時域內(nèi)的局部最優(yōu)調(diào)度。仿真結(jié)果表明滾動時域調(diào)度策略下，PSO算法在解決工件密集到達(dá)以及調(diào)度周期較長的批調(diào)度問題時優(yōu)化性能較好。同時，隨著調(diào)度周期增多，懲罰函數(shù)越能影響調(diào)度效果。但調(diào)度時域內(nèi)局部懲罰函數(shù)的設(shè)定并未有統(tǒng)一的標(biāo)準(zhǔn)，決策人員只能根據(jù)調(diào)度目標(biāo)和實際調(diào)度情況進行調(diào)整。