基于屬性排查的軟件運行風險多目標控制仿真

張開利，李 俊

(1.遼東學院工程技術學院，遼寧 丹東 118003;2.廣州大學電子與通信工程學院，廣東 廣州 510006)

1 引言

目前，軟件行業產生了眾多以軟件項目研發進度延期、投資成本超支及運行質量缺陷為特征的軟件危機，其中軟件運行缺陷是損失最為慘重的危機之一。為完善軟件運行質量，就要對其運行風險采取有效評估，并依照真實的風險情況使用必要的控制措施，最大限度降低風險[1-2]。在軟件研發與實踐中，由于人力、資金或時間等方面的限制，無法有效識別出全部的風險因素，且軟件運行風險會伴隨時間的推移產生風險積累與擴散，不同的風險屬性之間會互相作用與影響[3]。

針對上述問題，本文將傳統軟件運行風險控制目標延伸為多個，同時全面總結軟件風險之間的屬性問題，提出一種基于屬性排查的軟件運行風險多目標控制方法。規劃不同的軟件屬性項目，使用自乘運算推導出所有屬性影響值，并在屬性間的影響邊中代入影響值，使用可達矩陣理論規范化直接影響矩陣，計算各個軟件屬性影響的延伸水準，起到軟件全局質量評估作用；通過風險相關性，構建軟件運行風險多目標控制模型，使用多目標粒子群算法進行模型求解，實現高效精準的軟件運行風險控制。

2 基于屬性排查的軟件質量評估方法

軟件運行風險多目標控制之前，首先要全方位分析軟件目前的整體狀態，判斷軟件運行是否存在風險行為，提出一種基于屬性排查的軟件質量評估方法。軟件屬性排查過程中，將軟件可信度當作軟件質量的外在表現，將軟件運行時產生的因素屬性叫作軟件可信度屬性，將可信度屬性記作表1。

表1 可信度屬性列表

軟件屬性排查時，設定兩個基礎假設，即數量假設與質量假設。數量假設就是在屬性影響模型內，若一個節點至其余節點的邊越多，表明此節點屬性越重要。質量假設表示一個節點對另一個節點的影響數值越高，表明節點的屬性越重要[4]。

在上述假設前提下，計算軟件屬性影響數值，并更新全部屬性影響值，直至更新結束。屬性影響模型內，若節點B擁有一個面向節點A的邊，證明B的屬性權重較高，則將B的權重作為一個影響值的總和。

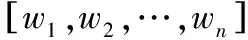
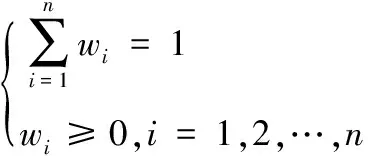
(1)

為排查出軟件屬性之間的影響水平，在屬性之間的影響邊內引入影響值lij，即

(2)

將屬性影響模型表示為鄰接矩陣P，矩陣P描述模型內的屬性節點關聯[5]。若節點i到節點j有入邊，影響水準為lij，影響指數為βij，那么pij=βijlij，反之pij=0。由此將矩陣P定義為

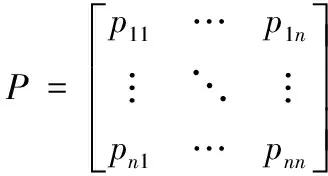
(3)

為詳細分析軟件屬性影響，按照可達矩陣理論，優化直接影響矩陣[6]，再利用自乘運算獲得綜合影響矩陣，即計算出各個軟件屬性影響的延伸水準的總和T：

T=G1+G2+…+Gn

(4)

得到綜合影響值后就能排查出屬性在軟件內對其余屬性的影響程度，然后給影響較多的屬性更大的權重值，歸一化后即可明確屬性權重，評估軟件運行的整體質量。線性映射綜合影響值，得到最終的屬性排查解析式為

(5)

3 基于相關性分析的軟件運行風險多目標控制模型

明確軟件運行的實時狀態后，若軟件運行存在較大風險，證明軟件質量存在缺陷，需建立一個風險多目標控制模型。設定軟件運行風險集合是{Ri|i=1，2，…，n}，n為風險數量。RE為風險損失預期值，RIi為風險評估值。假設第i個風險形成的損失為Li，由此得到

REi=RIiLi

(6)

本文構建的多目標控制模型中，關鍵控制兩個目標為最小：風險的損失預期值最小和風險控制成本最小[7]。在式(6)基礎上，組建軟件運行風險多目標控制優化控制模型

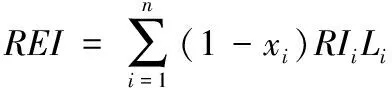
(7)

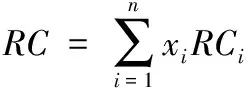
(8)

其中，xi為風險系數。由于xi的值只能是0或1，因此組建的多目標控制模型為一個0-1規劃模型：

(9)

軟件運行風險之間具備一定相關性，在軟件運行風險多目標控制優化控制模型中代入一個風險相關性，構建相關性分析下的軟件運行風險多目標控制優化控制模型，提升多目標控制的精確性與實用性。

本文所描述的軟件運行風險為在某個固定環境下的某個時段中，產生風險的不確定性和風險引發的經濟損失。風險的相關性包含概率與損失兩個因素，著重考慮損失因素的相關性。描述風險相關性的核心指標就是交互性指數，交互性指數代表兩個風險間的表現出的正相關聯系，取值范圍在[-1，1]，正數就是兩個風險同時產生的損失總和要高于單獨產生的損失總和，0代表兩個風險在損失水平上不具備相關性，也就是風險之間互不影響，損失展現出可加性特征；負數代表兩個風險之間的負相關，即兩個風險同時產生的損失總和低于單獨產生的損失值。

若風險i與風險j是擁有相關性的風險，設定Iij是其交互性指數，則Iij=Iji。Lij是兩個相關性風險同時產生的相關性損失，則Lij=Lji。

Choquet積分為一種模糊積分[8]，能夠很好地處理軟件屬性之間的互相作用問題，利用模糊集的模糊測度把相關數據代入屬性控制流程，衡量風險相關性損失水平。按照Choquet積分定理，集成算子和Lij值相等，則

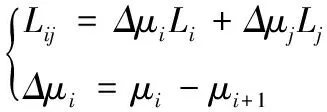
(10)

其中，μi為通過第i個風險構成的模糊集合的測度值。將基于2-可加的模糊測度值描述成

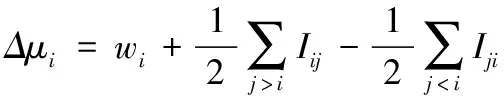
(11)

其中，wi為第i個風險權重，Iij、Iji分別為兩個風險的交互性指數。

將風險損失值引入風險多目標控制模型內[9]，設定REC是基于風險相關性損失后的損失期望值，則REC的推導公式為

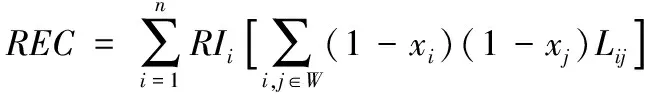
(12)

其中，W表示具備相關性的風險集，i，j∈W為兩個風險間的相關性，由于xi、xj的值只能是0或1，只要控制二者中的一個風險，即xi、xj的值有一個等于1的情況下，軟件運行風險就不具備相關性。

融合單風險損失預期值REI，獲得風險相關性下的風險損失預期值：

RE=REI+REC

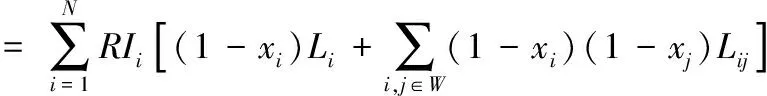
(13)

則最終的軟件運行風險多目標控制模型表達式為

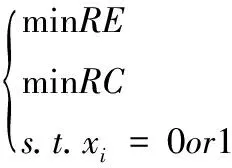
(14)

4 多目標粒子群算法下風險多目標控制求解

多目標粒子群算法為一種優化方法，將其代入運行風險多目標控制模型中完成模型求解，可幫助軟件開發者進一步優化軟件運行過程，規避有可能存在的運行風險，保證軟件應用穩定性與安全性。

背包問題為優化定理內的一種多目標優化方式[10]。該方法使用一個背包輸送不同物品，貨物的價值越高，輸送成本越低，與此同時，輸送貨物質量不可高于固定閾值，將以上輸送需求描述成

s.t.CX≤Z

(15)

式中，i代表貨品類別，M為各類貨品包含的貨品個數，P為貨品價值矩陣，V為體積矩陣，C表示質量矩陣，X代表挑選矩陣，Z是質量約束矩陣。

粒子搜尋面積[11]通過不同的約束條件進行規劃，若一共有m只鳥處于D維空間完成搜尋任務，則粒子群算法的運算過程為：

步驟1：初始化。設定Xi={xi1，xi2，…，xiD}是粒子i的初始范圍，Vi={vi1，vi2，…，viD}是粒子i的原始速率，數據集Pi={pi1，pi2，…，piD}可以記載粒子i遍歷過的方位內目標函數最佳值相對的方位，數據集Pg={pg1，pg2，…，pgD}可記載全部粒子遍歷方位內目標函數最佳值相對的方位。

步驟2：迭代。每個粒子的方位與速率更新解析式為

(16)

式中，d∈[1，2，…，D]，w代表上個時段的方位與速率對目前粒子的影響，c1、c2為學習因子，r1、r2為擾動系數，利用擾動系數能提升搜尋時每個粒子遍歷方位的隨機性，防止方法產生局部最優情況。

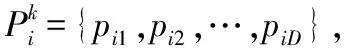
步驟4：終止迭代。終止迭代包含如下條件：若干次迭代后，方位Pg無更新情況，且在指定次數中，方位Pg相對的目標函數值改變量低于固定臨界值。

針對軟件運行風險控制多樣性需求，代入一個非劣解，創建多目標粒子群算法。在多目標控制可行域內，多目標粒子群在迭代時對收集和記載全部遍歷過程中產生的非劣解[12]，綜合全局最優解就能構成下一輪粒子進化的速率與方向，持續循環上述過程后就能推導出軟件運行風險多目標控制模型的帕累托最佳解，如果最佳解內的決策變量是1，證明軟件運行風險得到很好的控制，實現期望軟件運行風險控制目的。計算過程為

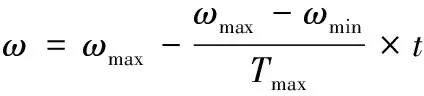
(17)

v(t+1)=ω×v(t)+c1×rand(0，1)×(xbest-x)+

c2×rand(0，1)×(xgbest-x)

(18)

其中，Tmax為最高迭代次數，t為目前迭代次數，ωmax、ωmin分別為ω的最大與最小值，xbest表示粒子本身的最佳值，xgbest為全局最佳粒子值。

處理了最佳解選擇問題后，還要注意迭代時產生的迭代規則問題，也就是一次迭代后得到多個非劣解后，要明確唯一的Pi與Pg，確保迭代的持續更新。在Pg的挑選過程中，將擁擠度當作權衡準則獲得迭代后的最佳權值，在真實模型求解任務中，把目標空間等量劃分成若干小網格，將各小網格迭代后涵蓋的粒子個數看作網格中粒子的擁擠度，擇取擁擠度最低的粒子作為下一時段的迭代初始點。

5 仿真研究

為表明所提方法在實際應用中的可靠性，使用Matlab仿真平臺進行實驗，實驗環境為Intel Core i5處理器，8G內存，使用Web數據庫系統存儲軟件運行數據。選擇某中型軟件項目為研究目標，開發商是通過定量管理認證的軟件企業。在表1可信度屬性列表基礎上，細分如下幾點軟件運行潛在風險，控制成本關鍵是人力成本，單位是人/日。如表2所示。

表2 軟件運行風險屬性與控制成本

設置Tmax值為11000，c1與c2值均為0.7，非劣解集合容量為150，原始粒子個數是220，非劣解篩選密度是0.06。本文方法的運算結果是一組軟件運行風險多目標控制的帕累托最佳解集，集合內各個解在兩個控制目標上均無法同時優于其它解，結果如圖1所示，圖1中風險暴露值表示風險對軟件的破壞程度。

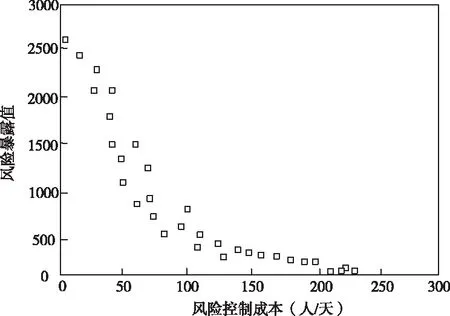
圖1 帕累托最佳解軟件運行風險多目標控制關系圖

從圖1可知，風險暴露值和風險控制成本目標呈現出非線性置換關聯，在控制成本為0時，表明全部風險均沒有得到有效抑制，這時風險總值最高。在風險暴露值是0的情況下，表明軟件運行得到很好控制，這時風險成本最高。軟件運行風險多目標控制中，一般是通過某些資源完成風險控制，但不能控制全部風險，這就要挑選恰當的風險目標完成運行優化，實現最佳風險多目標控制。圖2所示本文方法下的最佳解前沿準確清楚地刻畫出不同風險控制成本下的最佳控制策略，讓軟件研發者快速做出運行風險控制響應，維護軟件正常運行。

圖2為考慮軟件屬性與未考慮軟件屬性二種不同控制策略下的風險控制對比。

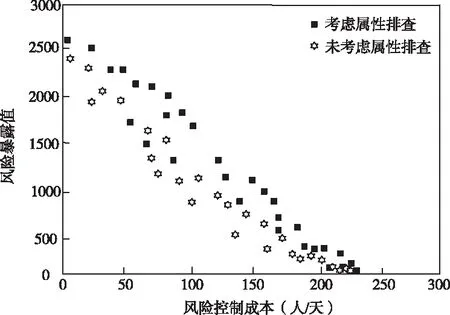
圖2 考慮屬性排查前后的風險多目標控制對比

從圖2看出，兩種控制策略結果存在很大區別，在同樣控制成本下，本文方法風險值要高于沒有考慮軟件屬性排查的風險值，證明本文方法不會局限于軟件淺層意義上運行風險，而是發掘出更多不易被發現的缺陷與漏洞，更貼合軟件真實運行風險控制現狀，對提升軟件運行風險管理水準發揮重要作用。

6 結論

針對軟件運行過程中存在的風險問題，提出基于屬性排查的軟件運行風險多目標控制方法。利用屬性排查評估軟件質量，構建軟件運行風險多目標控制模型，引入多目標粒子群算法完成模型求解，更全面地提取出軟件不同屬性之間的關聯，有效提高風險控制精度。