基于2D與3D匹配模型的變壓器全損耗特征計算

王 荊，潘莉麗，韓彥華，江天炎

(1.國網陜西省電力公司電力科學研究院，陜西 西安 710100;2.國網陜西電力公司西安供電公司，陜西 西安 710032;3.重慶理工大學，重慶 400054)

1 引言

電力變壓器繞組形變評估是影響其健康狀態和絕緣壽命的難點問題，準確計算變壓器全損耗，對變壓器繞組形變程度的準確評估具有的重要意義[1-3]。大容量電力變壓器正常運行時，其雜散損耗可以達到負載損耗的30%～40%，變壓器的內部損耗計算與分布規律分析對變壓器的經濟運行、降損和節能具有重要的意義[4，5]。然而隨著變壓器等級容量的不斷提升，其內部結構電磁關系也更為復雜，使用傳統的方法進行損耗分析往往具有較大的偏差。

在大型電力變壓器中，繞組線圈中流過較大的電流，不同的繞組結構產生的損耗值與分布也有所不同，同時在導體和鐵芯中產生銅損耗和磁滯損耗和雜散損耗，隨著電流數值的增大，雜散損耗會成倍增加，變壓器損耗分布和繞組熱點分布與變壓器散熱有著密切聯系，損耗計算是變壓器結構和絕緣配合設計的關鍵問題。文獻[6]中總結出了變壓器空載和滿載工況下的變壓器計算方法，并首先給出了相應的計算公式。文獻[7]中提出了一種改進的諧波損耗公式計算方法。文獻[8]中基于有限元法建立了變壓器二維有限元模型，得到了繞組的渦流損耗計算模型。文獻[9]分析了單相三柱變壓器的鐵芯損耗，構建了基于MAGNET軟件的變壓器損耗瞬態計算方法。文獻[10]建立了簡化的變壓器三維有限元模型，分析了變壓器的漏磁分布并計算了金屬結構件的損耗。這些方法可以分為兩類，一類是通過試驗或經驗總結的公式計算方法，該法計算方法簡潔、效率高且易操作，但是對于大型的電力變壓器而言，其具有更加復雜的結構，用此方法進行損耗的估算具有較大的偏差。另一種是基于計算機技術，利用有限元數值計算的方法來分析變壓器的損耗，隨著計算機技術的發展，該法能夠在保證復雜結構變壓器損耗計算效率的同時，還能夠具有較好的精度，受到國內外學者的青睞[11，12]。

然而，現有變壓器的損耗計算模型難以實現變壓器全損耗的計算，沒有考慮到不同類型的損耗一體化表現，其主要原因在于3D的損耗計算模型涉及到空間尺度的問題，繞組損耗的計算所需要的較小離散單元對于變壓器大空間的雜散損耗的計算而言，常常會導致空間離散的的失敗或單元的過度扭曲，難以保證計算的收斂和準確性。因此本文提出了一種基于2D與3D模型匹配的變壓器損耗混合模型計算方法，能夠準確計算繞組等損耗分布特征同時保證計算的收斂與高效性。并以一臺400 kVA的三相電力變壓器為例，分析了建模的基本方法和理論并對變壓器內部損耗的特征規律進行了分析，為工程設計制造提供參考，對提高變壓器穩定性與可靠性具有重要意義。

2 基本建模與耦合控制方程

2.1 有限元混合模型

有限元法(Finite Element Method，簡稱 FEM)，將整個求解域化分為一定數量的有限單元，各單元之間通過節點相連，應用求解的邊界原理和選取適當的形函數，分別求解每個單元，再將結果匯總起來，便可以得到整個區域的解[13]。

本文以一臺容量為400 kVA的三相電力變壓器為例，其基本參數見表1。

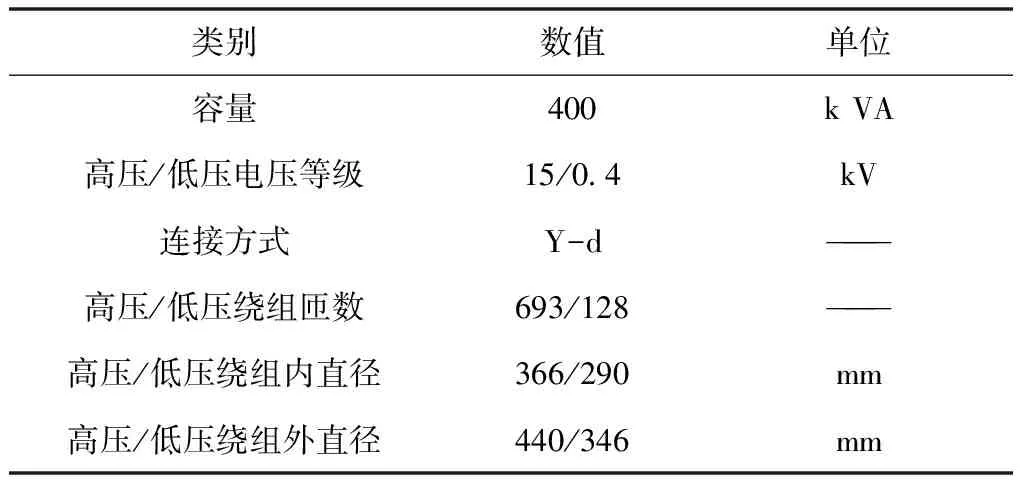
表1 變壓器基本參數

變壓器內部結構復雜，零部件眾多，在搭建有限元模型時應依據研究目的對變壓器模型進行適當簡化，從而計算結果的有效性與準確性。變壓器損耗計算主要包括繞組銅損耗，鐵芯的磁滯損耗和周圍結構所產生的雜散損耗，在搭建有限元模型時，主要針對鐵芯、繞組以及繞組周邊的結構件進行建模，主要包括固定零部件與變壓器外殼，如圖1。同時為計算繞組電流密度的分布及銅損耗，搭建了與3D模型相匹配的2D對稱模型，低壓繞組包含4根平行導線，尺寸為3.5×12 mm，高壓繞組截面為2.3×3.7 mm，如圖2。

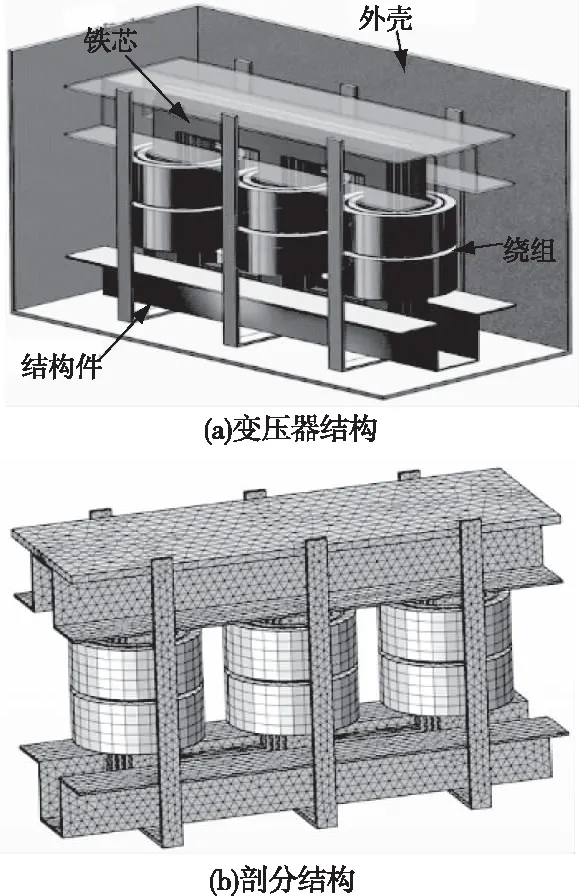
圖1 變壓器內部簡化結構

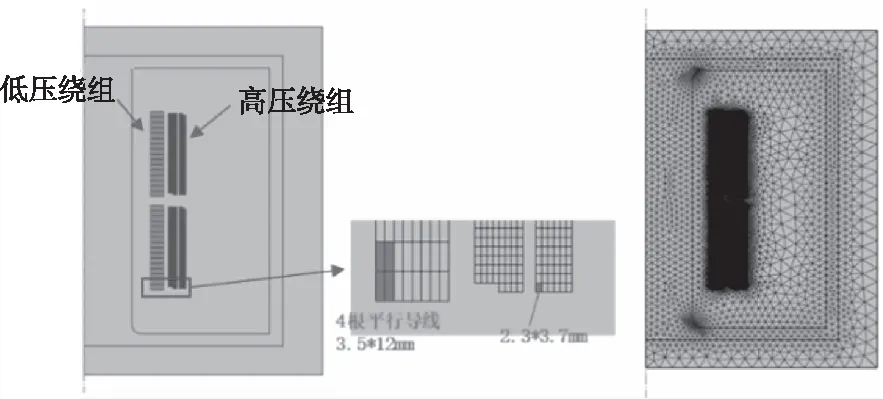
圖2 繞組模型

2.2 磁場分布計算

本文建立如圖1所示的電磁場計算模型，并且利用有限元法計算了變壓器內電磁場的分布情況，如圖3所示。電磁場計算邊界控制方程如式(1)、(2)所示[14]。

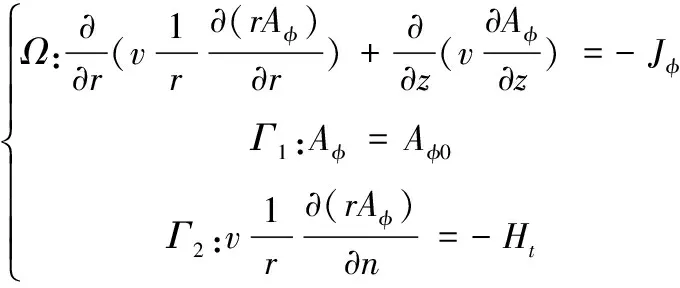
(1)

式中：Aφ為磁矢勢，v為磁阻率，Jφ為源電流密度，Ht為切向磁場強度。磁通密度由下式計算。

(2)

式中：Br和Bz分別為徑向和軸向磁感應強度。

如圖3所示為變壓器在運行時鐵芯和繞組的磁場密度分布情況，在鐵芯的上下鐵軛的磁通密度較大，最大值出現在靠近線圈的拐角處。而在繞組中磁通密度的分布呈現橢圓形，最大值出現在高壓繞組夾縫的中間位置，約為0.1T。

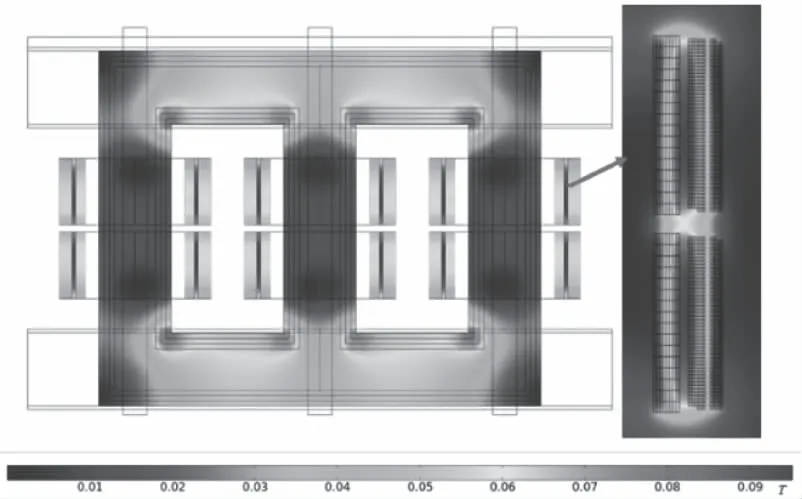
圖3 磁場密度分布

2.3 損耗計算

變壓器損耗主要分為銅損耗、鐵芯損耗和雜散損耗。銅損耗主要為繞組電流產生的電阻熱損耗，以及由漏磁通與結構件作用產生的雜散損耗，可由式(3)、(4)計算。鐵芯損耗主要為鐵芯材料的磁滯損耗，可由式(5)公式計算。

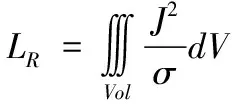
(3)

J=σE+jωD+σv×B+Je

(4)

P=k·fa·Bb

(5)

式中：LR表示阻性損耗，J表示電流密度，σ表示材料的電導率，E表示電場強度，D為電位移矢量，Je為外部電流。P表示單位體積鐵芯磁滯損耗，f和B分別表示頻率和磁感應強度，k、a、b為Steinmetz系數，此處k=100、a=1、b=1.6，本文所取鐵芯材料的BH曲線如圖4所示。

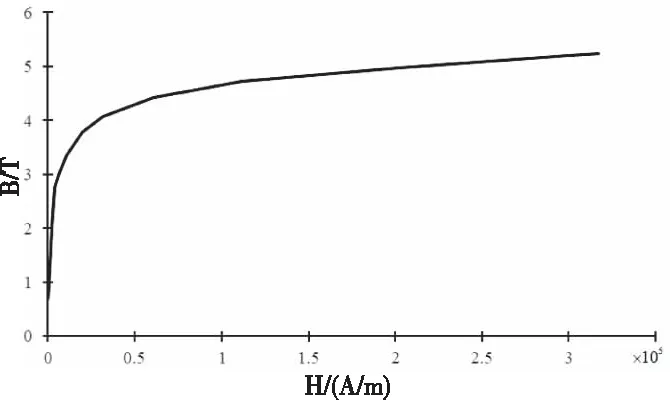
圖4 鐵芯材料BH曲線

3 損耗計算結果分析

3.1 鐵芯損耗及模型驗證

在開路條件下，利用本文搭建的有限元模型計算了鐵芯損耗，如圖5所示，磁場強度和磁通密度分布趨勢基本吻合，在靠近線圈的拐角磁場強度(5×103A/m)和磁通密度(2.5 T)較大，但仍處于線性區內，而在鐵芯的外圈的四個拐角磁通密度較小，約為0.5 T。如表2所示，本文計算模型所得鐵芯損耗約為1.54 kW，試驗結果為1.59 kW，誤差為2%，相對于傳統的經驗計算方法有較大的改善，同時證明了本文所搭建模型的準確性。

圖5 鐵芯的磁場強度(左半邊)與磁通密度(右半邊)

表2 結果對比

3.2 雜散損耗

雜散損耗是變壓器損耗計算的關鍵部分，由漏磁通與金屬構件相互作用產生渦流從而引起渦流損耗，其主要分布在固定結構件與油箱壁。如圖6所示為變壓器面電流密度分布情況，固定夾件面電流主要分布繞組側的上下兩個端面上，最大值約為5.81×103A/m；由于金屬夾件的屏蔽作用，油箱壁面電流主要分布在與繞組齊平的表面上，最大值最為7.36×102A/m，而在油箱壁上下兩面和拐角處面電流密度較小。

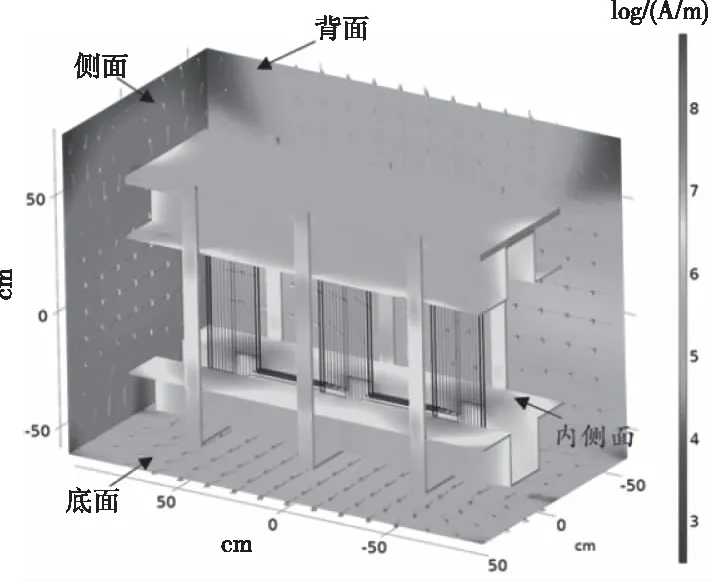
圖6 電流密度分布

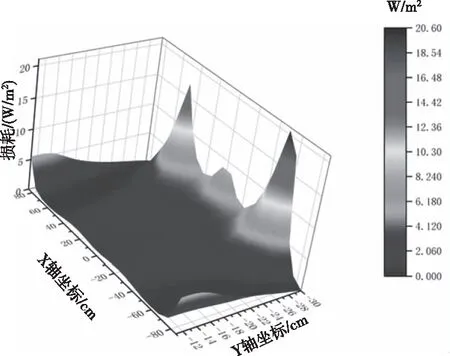
圖7 變壓器夾件內側面雜散損耗分布

圖8 變壓器油箱壁側面雜散損耗分布

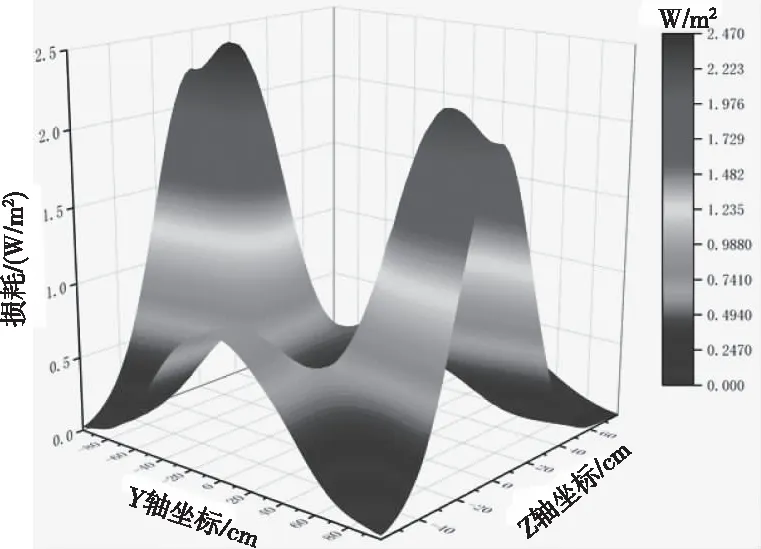
圖9 變壓器油箱壁背面雜散損耗分布

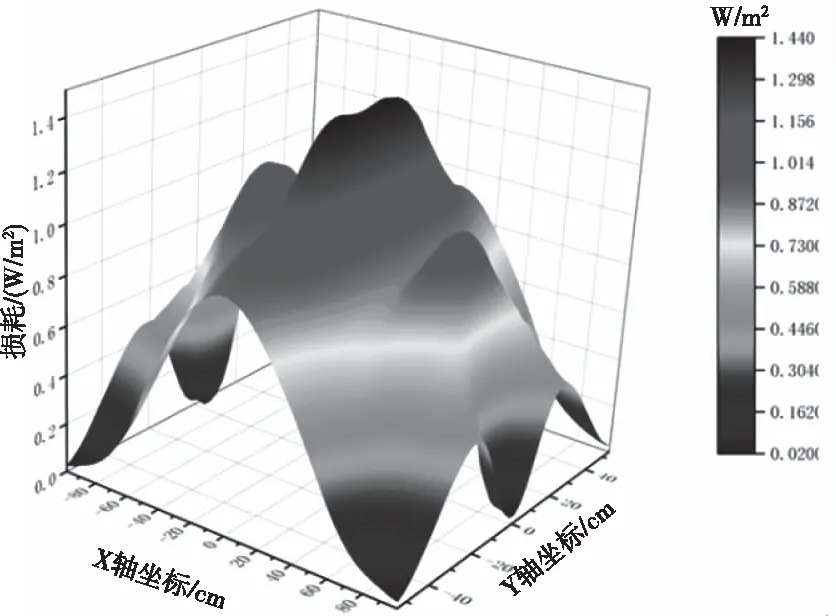
圖10 變壓器油箱壁底面雜散損耗分布

如圖7～圖10所示為固定夾件內側和油箱壁的損耗分布，夾件的內側面包含上下四個面，且各個面損耗分布規律基本相同，損耗主要集中在貼近線圈的邊緣附近，最大值約為20.6 W/m2；在變壓器油箱壁的側面，損耗分布整體呈現為拋物面形狀，最大值出現在中心區域約為7.48 W/m2；在變壓器油箱壁的背面，損耗分布整體呈現為“駝峰”形狀，在油箱壁背面的左右兩側分別包含損耗的兩個極大值峰，最大值約為2.47 W/m2，而在中心區域則是損耗的波谷區；在變壓器油箱壁的底面，損耗分布包含一個極大值峰出現在中心區域，最大值約為1.44 W/m2，和兩個較小的峰分布在兩側，周邊區域損耗值較小。

3.3 銅損耗

銅損耗為繞組電流流經導體產生的熱損耗。在變壓器中，繞組處在復雜的電磁環境中，由式(4)可知，電流密度的分布收到磁場等多方面的影響，線圈內部電流分布并不均勻。如圖11所示，在低壓繞組中，單匝線圈包含4根平行導體，電流分布整體偏向于高壓側和繞組兩端方向，而在高壓側電流分布主要偏向于低壓側和繞組兩端方向。由此所產生的損耗分布如圖12所示，分布趨勢與電流密度的分布基本吻合，趨近于高壓繞組之間的夾縫和繞組兩端方向。

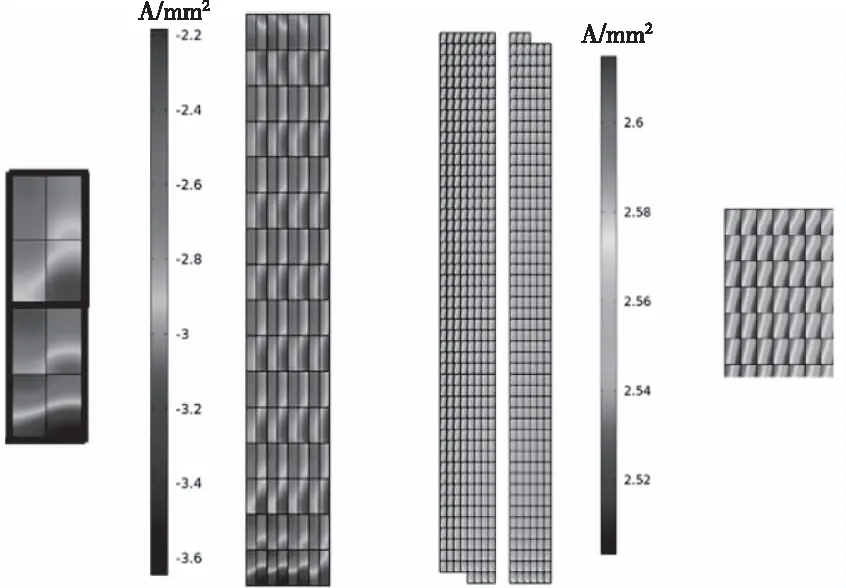
圖11 繞組內電流密度分布

圖12 繞組內損耗分布

4 結論

本文依據有限元理論設計了三項電力變壓器的損耗計算模型，相對傳統的方法，不僅能夠更為準確地計算變壓器各項損耗數值，同時還能夠對變壓器內渦流和損耗的分布規律與特征進行分析，得到的結論如下：

1)基于有限元法，提出了一種基于2D與3D模型匹配的變壓器損耗混合模型，能夠很好的解決變壓器建模的空間尺度問題，在降低計算量的同時兼有計算的準確性。

2)變壓器內部固定夾件的雜散損耗主要分布于夾件的內側面，并集中于靠近線圈的邊緣，最大值約為20.6 W/m2，在油箱壁側面、背面和底面損耗分布呈現拋物面形、“駝峰”形和“三峰值”形。

3)高低壓繞組損耗分布趨勢與電流密度的分布基本吻合，整體繞組和導體內部損耗分布趨近于高壓繞組之間的夾縫和繞組兩端方向，對于變壓器繞組的熱點計算和變形評估具有一定的指導意義。