3D打印氧化鋯復合漿體的MRT LBM流動分析

孫健華，顧 海，2*，姜 杰，2，李 彬，2

(1.南通理工學院機械工程學院，江蘇 南通 226002;2.南通理工學院江蘇省3D打印裝備及應用技術重點建設實驗室，江蘇 南通 226002)

1 引言

陶瓷材料已廣泛應用在諸如電子、航空、藝術、建筑、生工以及化工等重要的工業領域，皆是由于此類材料具備穩定好，抗腐蝕以及耐高溫等其它材料無法取代的優點，但是成形難的特點限制了它的進一步應用發展。近些年來，增材制造技術的出現為陶瓷粉末材料的成形提供一種新的思路。目前可應用于陶瓷材料中的3D打印工藝主要包括光固化成形(Stereo Lithography Apparatus，SLA)[1-3]、噴射打印成形(Ink Jet Printing， IJP)[4]、三維印刷成形(Three-dimensional Printing，3DP)[5-6]、選區激光燒結成形(Selective Laser Sintering， SLS)[7-8]、選區激光熔化成形(Selective Laser Melting， SLM)[9-10]、熔融沉積成形(Fused Deposition Modeling， FDM)[11]以及漿料直寫成形(Direct Ink Writing， DIW)[12]等六類主流工藝。根據工藝復雜性，除DIW工藝外，其余四種工藝均需要依賴激光器實現成形。在目前的DIW中，陶瓷漿料的擠出普遍采用的是類似注射器形式結構，利用氣壓或液壓進行驅動實現漿體擠出，此種結構占用體積大，結構復雜。除了此類擠出形式外，螺桿擠出形式作為一種常見形式已有效應用在流體加工、食品運輸等相關領域，這里將選用此結構替換原有的擠出結構。

為了進一步分析陶瓷復合漿料在螺桿螺道內的流動，擬采用介觀數值模擬方法MRT LBM對其進行仿真分析，此方法作為一種編程實現的數值分析方法，具有物理過程清晰，方便計算的優點，避免了傳統的有限元方法在計算復雜流體流動時可能出現的發散情況[13-15]，這里將結合MATLAB軟件進行分析計算。

2 氧化鋯復合漿料的制備及流變方程的建立

這里的陶瓷漿料涉及的原始粉末為納米級的氧化鋯材料，選用苯偶酰、季戊四醇三丙烯酸酯以及甲基丙烯酸甲酯作為原始溶劑，利用高速攪拌機充分混合原始溶劑后，緩慢加入氧化鋯粉末，并繼續使用高速攪拌機加速粉末的充分溶解，通過測定最終復合漿料的固相含量為64.9%。

為了獲取氧化鋯復合陶瓷漿體的流變方程，利用Rheolab MC1型粘度計進行了粘度測試試驗，實驗時溫度為20℃，選用三種非牛頓流體模型作為備選模型，通過MATLAB擬合獲得相應的相關系數R2如表1所示。

表1 三種模型擬合相關系數R2對比

結果表明，Herschel-Bulkley流體的流變方程更符合此處的模型，具體的方程為

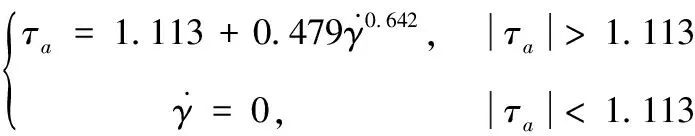
(1)

根據Papanastasiou T C等人對非牛頓流體的介紹，對式(1)進行了變換，并獲取其粘度方程為

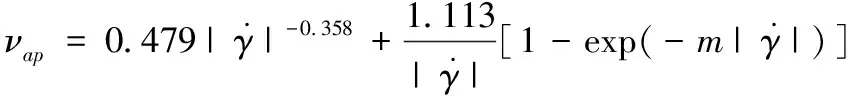
(2)

式中參數m越小時，對應的流體越接近于冪律流體，當m趨向于無窮大時，對應的流體即傾向于Herschel-Bulkley流體，這里m=600。

3 MRT LBM流動分析

3.1 單螺桿擠出結構模型

螺桿的基本結構圖如圖1所示，它的關鍵尺寸如表2所示，將其充分展開后呈現出如圖2所示的腔體，氧化鋯復合陶瓷漿體在原螺道內的流動即可轉換成其在腔體內的流動。

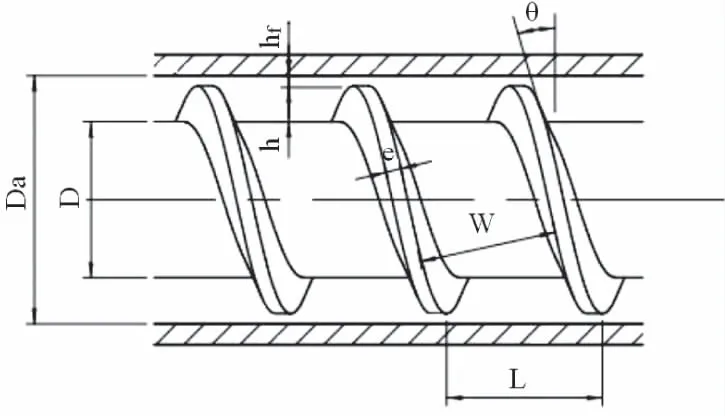
圖1 螺桿結構

表2 螺桿的關鍵幾何參數

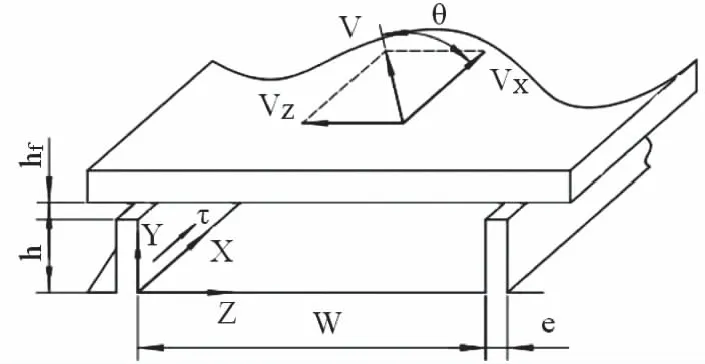
圖2 螺桿展開結構

3.2 復合陶瓷漿體的MRT LBM流動分析

3.2.1 MRT LBM在非牛頓流體中的應用

多松弛時間參數的LBM與單松弛時間參數的LBM主要區別在于MRT LBM涉及到矩空間的轉換[16]，則其基本方程將轉變為

f(r+eiδt，t+δt)-f(r，t)

(3)

速度配置ei描述如下[17]

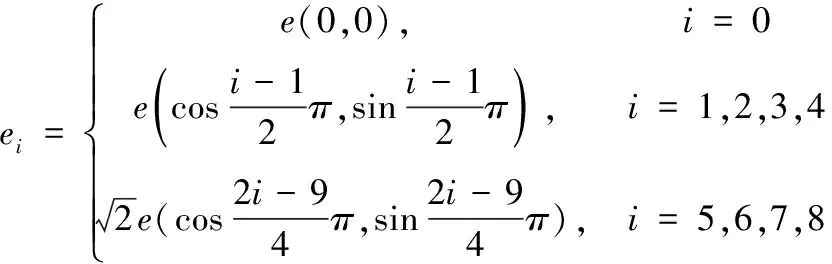
(4)

式中基本速度量e的大小為格子步長δx和時間步長δt的比值，通常情況下，兩者均取為1，那么e=1。宏觀物理量速度u，密度ρ可以根據平衡態分布函數以及格子聲速獲得，具體如下式所示[18]

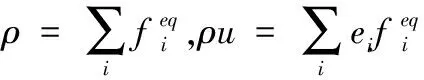
(5)

進一步地，上式中的f(r，t)和feq(r，t)兩項可以通過中間變換矩陣M轉換為矩空間ρ(r，t)和ρeq(r，t)，具體計算公式為ρ(r，t)=Mf(r，t)，ρeq(r，t)=Mfeq(r，t)，其中M具體為[19]

(6)

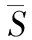
(7)

在模型中，s0，s3，s5均是與密度和動量相關的參數，而密度和動量皆為守恒量，因此它們的值為0，s7和s8是與松弛過程相關的量，取值為1/τ，τ為單松弛參數LBM模型中的松弛時間，而剩余的參數通常取稍大于1的數即可，這里s1=s2=1.3，s4=s6=1.1。在使用MRT LBM進行流體分析時，其基本過程主要由碰撞和遷移組成，其中遷移步的表達形式為

f(r+eiδt，t+δt)=f+(r，t)

(8)

其中f+(r，t)即為碰撞后的密度分布函數，碰撞步與單松弛參數的LBM不同，具體方程為[20]

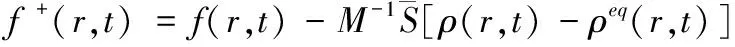
(9)

在MRT LBM中，應變率張量比單松弛參數LBM復雜，可以推導得到

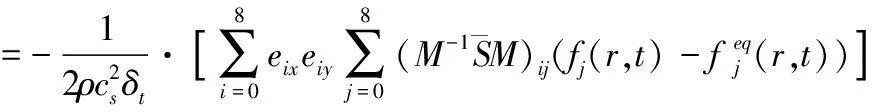
(10)

應變率張量的第二不變量DII可以描述為

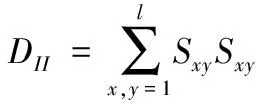
(11)

非牛頓流體的動力粘度主要與松弛時間τ和密度ρ相關

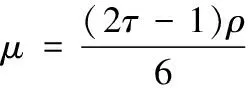
(12)

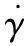
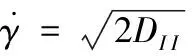
(13)

在利用MRT LBM進行實際模擬計算時，其主要過程描述如下[17-20]：

1)確定物理模型的主要基本參數，如計算域，初始速度或壓力值，密度等；

2)根據式(3)計算并確定平衡態分布函數；

3)根據式(10)計算應變率張量；

4)結合式(5)和式(12)，以及非牛頓流體的本構模型可以計算獲得當前計算循環步內的松弛時間τ；

5)碰撞步和遷移步計算，主要參考式(8)和(9)。

6)邊界處理這里主要選擇非周期性邊界條件；

7)根據式(5)計算密度和速度；

8)返回第3)步執行下一次循環計算。

3.2.2 復合陶瓷漿體的流動分析

取圖2中的Y-Z組成的截面，根據螺桿擠出的實際運動，將速度僅設定在與Z方向一致的上表面，根據表1中列出的螺槽的幾何尺寸，設置模擬時的格子數為240×180，螺桿的轉速設定為N=36 r/min，通過模擬分析可以獲得如圖3所示的流線圖。

橫截面流動區域的上側為螺桿外筒的內壁，左右兩側分別為螺桿螺槽的兩個壁面，下側則對應螺桿桿芯的外壁，根據圖3可以看出，流場的中心在 (4 mm， 4 mm)附近，其更接近于螺桿的外筒，除了沿螺道方向前進外，漿體在相鄰兩個螺棱內壁之間存在環流。在螺棱與螺桿外壁形成的角落里則沒有明顯流動存在。

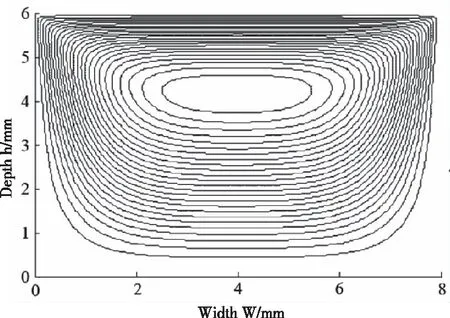
圖3 漿料在Y-Z截面的流線圖

在進行獲取速度分布圖時，為了進行對比，同時進行了格子數為160×120的MRT LBM和LBM數值分析，結果如圖4-圖5所示，它們的結果相近，因此可以認為本文中提出的方法是切實可行的。通過理論建模結合編程的形式實現對流體流動的研究，也為分析解決流體動力學問題提供了新的思路。圖4a)和圖4b)分別給出了螺槽深度h=4 mm處的度分量u和速度分量v的分布情況，明顯的是，越接近于螺桿，速度分量u越大，速度分量v的極限值出現在環流中心處，而在邊界處速度分量v均比較小。圖5a)和圖5b)分別給出了螺槽寬度W=4 mm處的度分量u和速度分量v的分布情況，速度分量u在螺棱壁面附近趨近于0，速度分量v在螺槽流道中部基本為0，逐漸往螺棱靠近時，速度也逐漸發生變化。

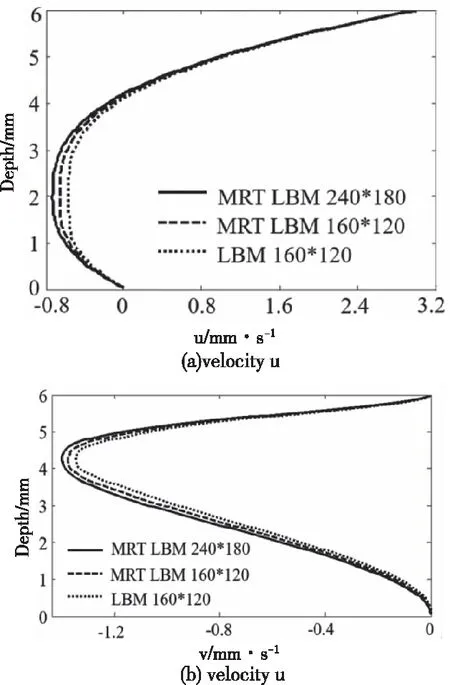
圖4 速度分量沿螺槽深度的分布

圖5 速度分量沿螺槽寬度的分布

4 結束語

針對陶瓷3D打印，對原有供料結構進行了改進，并利用MRT LBM對氧化鋯復合陶瓷漿料在該螺桿結構中的流動進行了分析，可以獲得以下結論：

1)根據流變測試結果，氧化鋯復合陶瓷漿體的流變特征呈現出典型非牛頓性流體特征，與Herschel-Bulkley流體較為貼切。

2)利用MRT LBM可以有效對復雜非牛頓流體進行流動分析，編程過程簡單，避免對復雜微分方程的求解。

3)對氧化鋯復合漿體在擠出結構中的流動分析可知，陶瓷漿體在噴頭橫截面的流動呈現環流特征，環流中心大致在(0.5W，0.67h)處。結合流線圖和速度分布圖可以總結得知，為了保證流體的流動速度，一方面可以適當增大螺桿的旋轉速度，另一方面可以適當增大螺槽的寬度。