基于機器學習的交叉覆蓋信息捕獲算法研究

劉 昆， 孟曉靜

(1.中國礦業大學徐海學院，江蘇 徐州 221008;2.徐州醫科大學醫學信息與工程學院，江蘇 徐州 221000)

1 引言

數據信息對于現代生產生活至關重要，通過分析挖掘可以從中獲得所需的價值信息。隨著數據信息的海量膨脹，給采樣收集過程帶來了巨大挑戰。受系統中復雜因素影響，采樣收集階段經常會產生信息的交叉覆蓋[1]。交叉覆蓋信息一般具有非相關特征或者混雜特征[2]，對數據分析形成干擾，導致信息理解偏差。因此，為了提高交叉覆蓋信息的利用價值和挖掘精度，改善交叉覆蓋信息的捕獲性能是關鍵[3]。一些學者針對特定場景下的交叉覆蓋信息捕獲提出了相應的解決方法。文獻[4]設計了一種MKELM算法，并通過極限學習實現CSP特征分類。此方法缺乏對數據分布的考慮，很容易出現過采樣或者欠采樣。文獻[5]設計了一種ARIRF算法，通過混合采樣達到樣本訓練目的。此方法能夠有效解決采樣問題，但是對數據非線性處理效果不夠理想。文獻[6]設計了一種EEGNets算法，通過不同的卷積策略實現神經網絡。此算法雖然在一定程度上表現出較好的泛化性和準確性，但是算法初衷存在局限，導致在穩定性和魯棒性方面表現不佳。

本文針對交叉覆蓋信息提出一種基于機器學習的捕獲算法。先對交叉覆蓋信息采取預處理，篩除其中的非關聯屬性。再利用互信息良好的非線性處理，提取信息主成分特征。最后設計了基于SLFN的機器學習，根據網絡輸出加權完成信息分類。通過Acc、F-Measure和G-Mean三個指標進行綜合檢驗，充分證明了算法的有效性。

2 非關聯屬性篩除

交叉覆蓋信息存在很多噪聲和缺陷，不利于直接進行數據分析，于是，先將交叉覆蓋信息采取預處理，去掉其中的異常特征。對于任意的交叉覆蓋信息，可以描述成集合C={c1，c2，…cn}，其中ci代表第i個樣本。假定ci包含的特征屬性數量是m，則ci可以描述成ci={ci1，ci2，…cim}，其中cim是對ci的第m個特征屬性描述。ci與cj為交叉覆蓋信息集合內的數據，它們和某屬性t的映射關系可以描述如下

(1)

(2)

(3)

其中，ave(ci)是c所在類的局部均值集；wi是對應的加權系數。基于上述分析，特征屬性t對應的加權描述如下

(4)

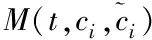
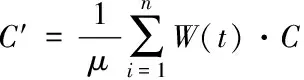
(5)

μ代表集合因子。C′保存了交叉覆蓋信息的重要屬性，同時篩除了其中的異常屬性，更有利于后續分析處理。

3 特征提取

經過預處理階段的非關聯屬性篩除后，交叉覆蓋信息存在大量的冗余數據，此時直接進行分類處理，不僅會增加很多無益消耗，也會降低信息獲取的性能。由于信息熵擅長描述未知信息量，因此這里利用信息熵對預處理后的數據做去冗余操作。非關聯屬性篩除得到的數據集標記為D，特征分布空間為Ra×b。假定D內任意數據Di=(di1，di2，…dib)，dij是描述數據i對應的第j個特征量，引入信息熵可得

(6)

R(Di，Dj)=H(Di)+H(Dj)-H(Di，Dj)

(7)

其中，H(Di，Dj)利用di與dj的聯合概率得到。R(Di，Dj)是通過對熵的量化確定特征屬性，所以它可以應用于非線性關系場合。對所有數據特征求解互信息，得到矩陣如下

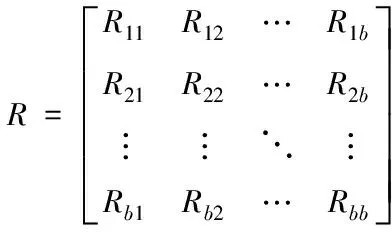
(8)

矩陣R內，R11，R12，…，Rbb為自信息，其余的均為互信息。如果變量間沒有關聯，則相應的互信息等于零，否則互信息一定大于零。并且，互信息滿足交換性，即Rtj=Rji，由此可得R為對稱矩陣。假定互信息R的特征值正序集合是r1，r2，…，rb，對應的特征向量是a1，a2，…，ab，則依據R特征值對互信息分解可得：R=A′∧A。Λ代表由r1，r1，…，rb構造的對角矩陣；A代表由(a1，a2，…，ab)構造的矩陣。根據R特征值計算主成分維度，公式如下

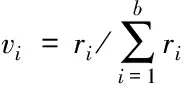
(9)

四種施工方式支護結構受力統計見表3，臺階法初支應力明顯較大，其他方法在施加臨時仰拱和中隔壁后等型鋼后，減小了初支因彎矩產生的應力，型鋼受力(見圖13)在47.0 MPa～60.1 MPa。臺階法和臨時仰拱臺階法，將鎖腳錨管焊接于鋼支撐上協調受力，能充分利用錨管鎖腳作用，而CD法和CRD法的中隔壁分擔了上部初支承受荷載，鎖腳作用變弱。

4 基于機器學習信息捕獲

(10)

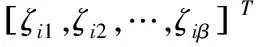
(11)

G是隱層輸出；O是理想輸出。為了限定網絡的復雜性，對(11)引入正則化處理，如下

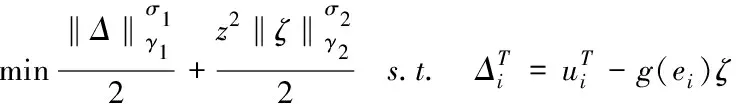
(12)

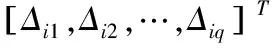
(13)

(14)

如果網絡中學習數據量超過N時，則U代表N×N階矩陣；否則，U代表M×M階矩陣。

5 算法評價指標

交叉覆蓋信息具有非平衡性，為防止捕獲算法向多數類偏向，以及其它因素導致評價偏差，選取Acc、F-Measure和G-Mean三個指標來綜合檢驗交叉覆蓋信息捕獲算法的性能。定義混淆矩陣如表1所示。其中Positive和Negative依次表示待預測的正負類；Positive′和Negative′依次表示預測結果的正負類。

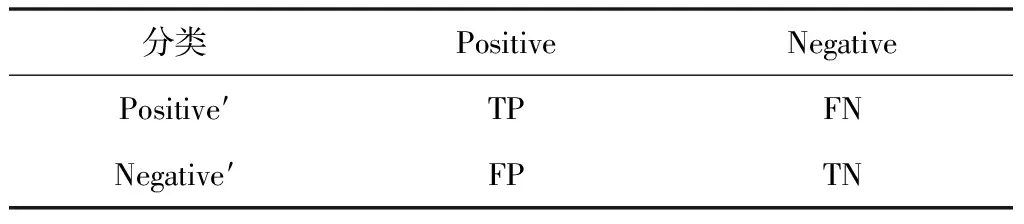
表1 混淆矩陣

Acc用于描述捕獲準確率，一般在計算準確率指標時，很多文獻只考慮了給定Positive被正確分類至Positive′的概率，忽略了Negative被正確分類至Negative′的情況。所以本文采用Acc，公式定義如下

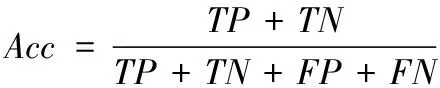
(15)

根據式(15)，信息捕獲的準確率同時受正負類的結果影響，該評價方式更加合理有效。

F-Measure用于描述捕獲精度與召回率的綜合性能。該指標不受時間序列影響，其值越大，說明分類效果越好。F-Measure公式定義為

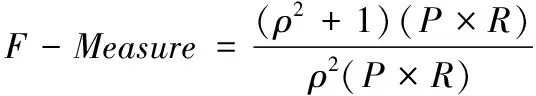
(16)

其中，P=TP/(TP+FP)表示Positive的分類精度；R=TP/(TP+TN)表示召回率；ρ表示加權調和系數。

G-Mean用于描述正負類召回率的綜合指標。該指標具有良好的魯棒性，僅當正負類的R指標均升高時，G-Mean結果才升高，有效防止非均衡數據等因素對Positive單方面的影響。G-Mean公式定義為

(17)

6 實驗與結果分析

為有效驗證交叉覆蓋信息捕獲算法的真實性能，采用表2所示的8個數據集，通過對折生成交叉覆蓋信息。特征維度最低18，最高1024，涵蓋低維和高維情況。為了保證檢驗的充分性，實驗除了采用多數據集，還引入MKELM[4]、ARIRF[5]和EEGNets[6]算法進行比較。

表2 數據集描述

通過仿真得到不同數據下算法的Acc指標結果，如表3所示。可以看出，由于不同數據集的特征維度與類別等參數的差異，給交叉覆蓋信息捕獲帶來的難度也不同，從而給捕獲的Acc指標帶來一定影響。madelon與GOIL20數據集復雜度相對較高，各方法在這兩個數據集下的Acc指標較小。本文算法的最小Acc為0.613，較MKELM、ARIRF和EEGNets分別高出0.142、0.069、0.055。最大Acc為0.982，較MKELM、ARIRF和EEGNets分別高出0.019、0.014、0.016。

表3 Acc指標結果

通過仿真得到不同數據下算法的F-Measure指標結果，如表4所示。可以看出，數據集特征維度與類別等參數的差異同樣會給捕獲的F-Measure指標帶來影響。在madelon與GOIL20數據集下各方法的F-Measure指標明顯較低。但是本文算法的最小F-Measure為0.571，仍然較MKELM、ARIRF和EEGNets分別高出0.125、0.046、0.020。最大F-Measure為0.991，較MKELM、ARIRF和EEGNets分別高出0.046、0.019、0.018。結合Acc與F-Measure結果，表明在各實驗數據集下，本文算法的捕獲準確率和召回率較其它算法都更具優勢，受數據集參數影響相對更小。

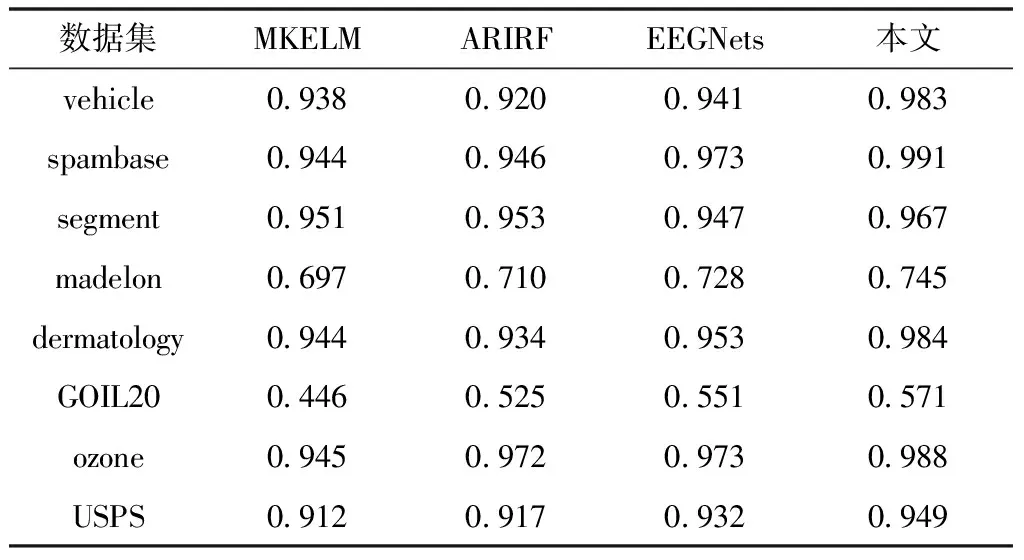
表4 F-Measure指標結果

不同數據集下的G-Mean指標結果如表5所示。可以看出，MKELM的G-Mean值波動范圍是0.799～0.968；ARIRF的G-Mean值波動范圍是0.855～0.941；EEGNets的G-Mean值波動范圍是0.880～0.972。本文算法的G-Mean值較MKELM、ARIRF與EEGNets波動范圍更小，更加穩定，且大部分情況下優于其它方法，魯棒性更好。

表5 G-Mean指標結果

基于實驗結果，本文算法在spambase數據集具有最好的綜合捕獲性能，于是基于spambase數據集，向其中添加噪聲數據，得到不同信噪比時的捕獲準確率Acc指標，結果如圖1所示。可以看出，各算法的Acc曲線走勢基本一致。本文算法在信噪比為30dB之前，捕獲準確率受噪聲影響嚴重，過了30dB，捕獲準確率快速上升，當信噪比為37.5dB時準確率達到最高。而其它Acc曲線上升時機都遲滯于本文算法，表明本文算法的抗噪性能更好。

圖1 Acc與信噪比關系曲線

7 結束語

為提高交叉覆蓋信息的捕獲效果，本文提出了一種基于機器學習的捕獲算法。首先對交叉覆蓋信息采取預處理，去掉其中的異常特征。然后根據信息熵對預處理后的數據做去冗余操作，并利用互信息矩陣提取主成分特征。最后設計了機器學習網絡模型，通過求解網絡輸出加權確定數據分類，實現信息捕獲。基于不同數據集的仿真，得到本文方法的平均Acc為0.895，平均F-Measure為0.897，平均G-Mean為0.939，各項指標均優于對比方法。表明本文算法具有更好的準確率和召回率，魯棒性和抗噪性得到顯著提升。