基于仿真的游樂設施模型優化與加速度測量

項輝宇，李 磊，冷崇杰，徐 銳

(北京工商大學，北京 100048)

1 引言

加速度是游樂設施的一項重要指標，游樂設施的設計既要追求驚險刺激的游樂體驗又要保證乘客對加速度的耐受和安全。為使乘客不受到傷害，游樂設施標準要求人體加速的限制在一定范圍內，我國人體加速度判定主要依據安全標準GB 8408-2018《大型游樂設施安全規范》[1]進行評價。目前，廣泛采用對加速度測量[2]的對象是設備，雖然將加速度測量的坐標原點定在座椅上方人體內臟處，但實際測量時，加速度的測量點固定在設備座椅上；雖然采用加速度傳感器或者加速度數據記錄儀可以精確測量設備加速度數值，但當游樂設施運行過程中，由于座椅、人體和其它構件的相互作用，導致人體加速度和座椅加速度產生差異，甚至經常會出現人體加速度[3]超過座椅加速度，因此測得的座椅加速度不是真正意義上的人體加速度，依據座椅加速度進行安全性評價具有明顯的局限性，因此，有必要建立座椅與人體之間的運動傳遞模型，明確人體和設備的響應關系，這對判定人體的加速度是否符合要求至關重要。

為了解決這一問題，本文選取如圖1所示5環過山車設計方案建立了座椅—乘客傳遞模型，根據Adams中模擬的到的座椅、下軀干、上軀干、內臟、頭部[4]等加速度實驗數據并對模型中的參數進行識別，得到完整的傳遞模型，對設備和人體加速度之間的響應關系提供了模型和量化，在此基礎上，可根據檢測獲取的座椅加速度進行人體特定位置的加速計計算，并進而依據有關標準進行乘載安全性評價 。

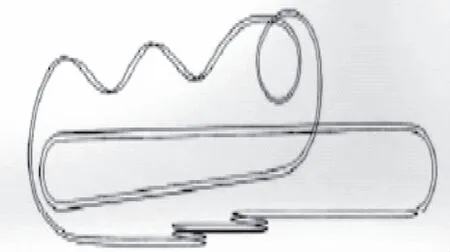
圖1 五環過山車軌道

2 人體-座椅傳遞模型建立

通過預模擬確定人體模型和座椅以及安全壓杠之間的定位，實現人-椅模型耦合如圖2示。

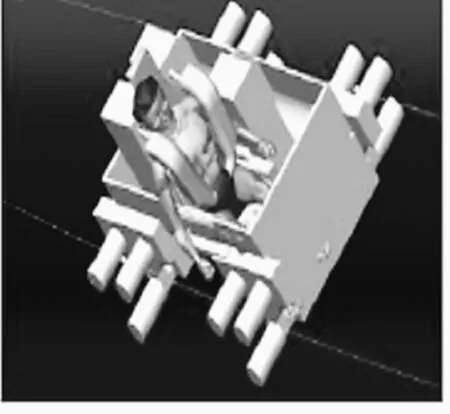
圖2 人椅耦合模型

依照標準中對乘客良好束縛的描述，按笛卡爾坐標對人體坐標系做如下規定，身體重心豎直向上方向為Z，前進方向為X，左右方向為Y，XYZ符合右手坐標規則。假定人體在X向和Y向的運動受到限制，本文主要探究Z方向乘客-座椅傳遞模型的響應關系。在Adams中模擬過山車從最高點開始運行到站臺的過程，輸出座椅、上軀干、下軀干、內臟、頭部的加速仿真數據。依據仿真數據繪制人體加速的隨時間變化圖像，結果如圖3所示。

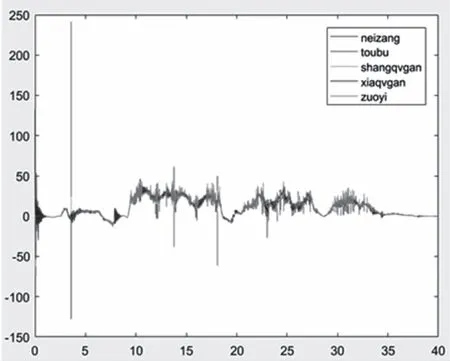
圖3 人體不同部位加速度

從輸出的結果來看，人體不同部位加速度的響應不同。在Z方向上的響應時間，梯度變化及響應結果存在顯著差異。通過仿真進一步說明采用座椅加速度代替人體加速度是不符合實際的。

從輸出的結果來看，人體不同部位加速度的響應不同。在Z方向上的響應時間，梯度變化及響應結果存在顯著差異。通過仿真進一步說明采用座椅加速度代替人體加速度是不符合實際的。

2.1 模型建立

為研究人體Z方向加速度[5]響應關系，特別是獲取人體內臟、頭部及上軀干等重要位置的加速度信息，文中建立了垂向3自由度如圖4 和4自由度[6]如圖5人體-座椅傳遞模型。其中垂向3自由度模型主要探究座椅-內臟-臀部傳遞鏈，垂向4自由度模型探究座椅-臀部軀干-頭部傳遞鏈。

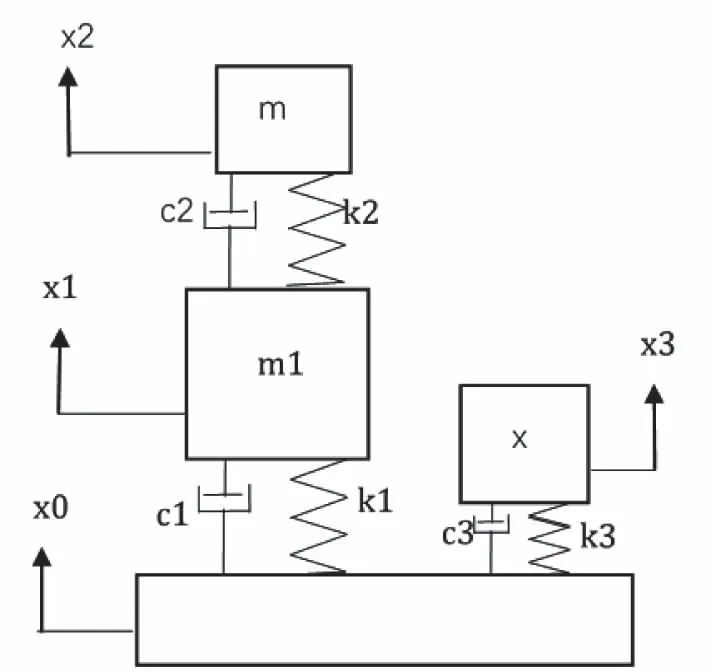
圖4 三自由度模型

根據3自由度模型建立傳遞函數微分方程如式(1)

(1)

在圖4中，m1為臀部，m2為內臟，m3為大腿；c1、k1分別為臀部剛度、阻尼；c2、k2分別為內臟剛度、阻尼；x0為座椅位移激勵、x1、x2、x3分別為臀部、大腿和內臟產生的位移。

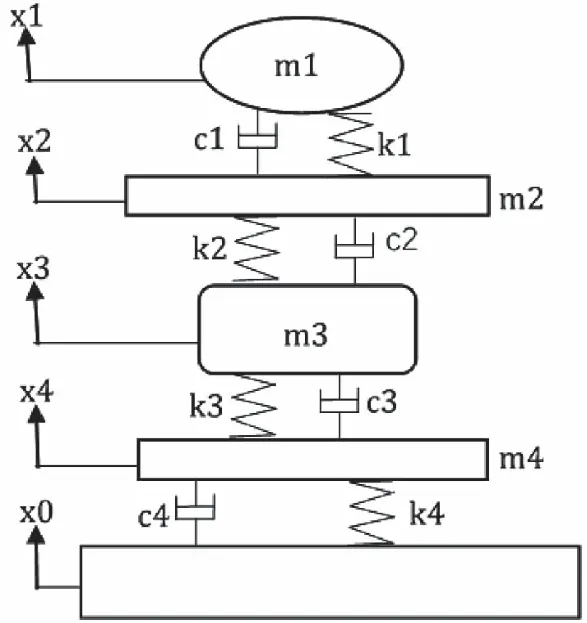
圖5 四自由度模型

圖5中，m1為頭部，m2為上軀干，m3為臀部，m4為下軀干；c1、k1為頸部剛度、阻尼；c2、k2為上軀干剛度、阻尼；c3、k3為臀部剛度、阻尼；c4、k4為下軀干剛度、阻尼；x0為座椅位移激勵、x1、x2、x3、x4分別為頭部、上軀干、臀部和下軀干產生的位移。

根據4自由度[7]模型建立傳遞函數[8]微分方程如式(2)：

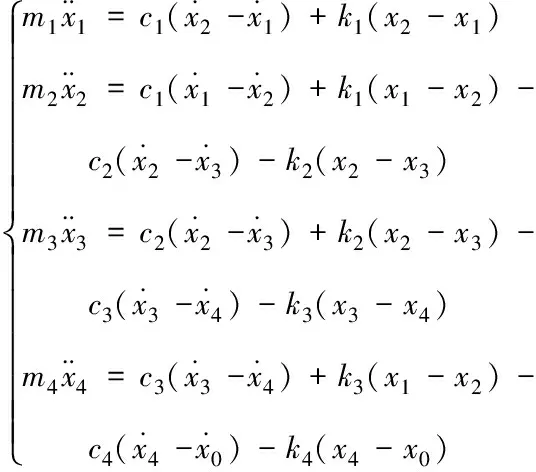
(2)

將式(1)和(2)兩組微分方程進行拉普拉斯變換，并令s=jw得到頻響函數如式 (3)和(4)如下

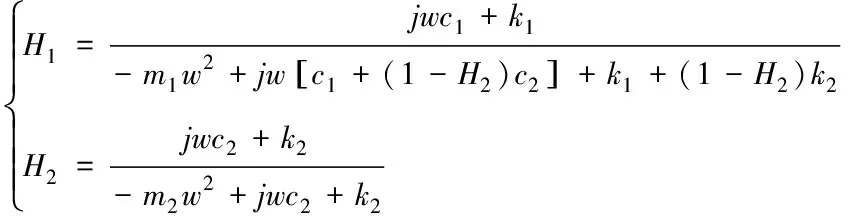
(3)

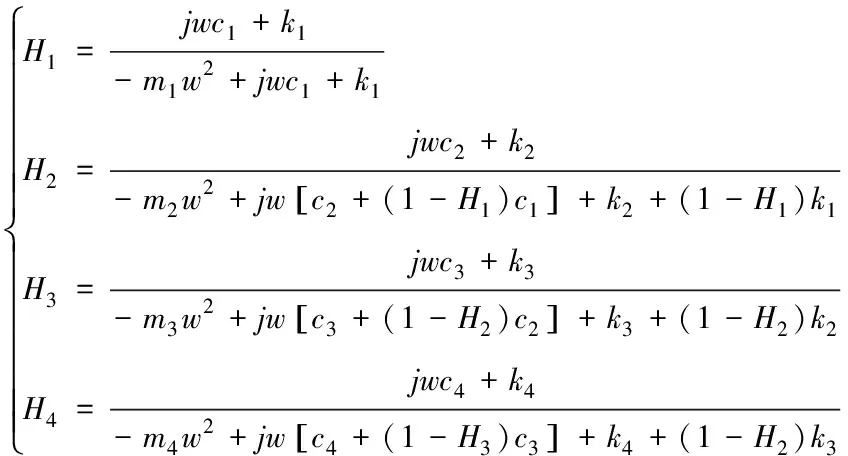
(4)

在上述模型中，人體各部分的質量、剛度和阻尼均為未知參數；因此，將模擬得到的座椅、下軀干、上軀干、頭部和內臟的仿真數據作為參數識別的依據，用最小二乘法將模擬結果擬合到上述兩個傳遞模型中，構建參數識別表達式J如式(5)

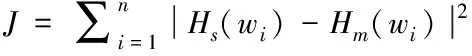
(5)

式中Hs表示仿真模擬得到的各部分頻響函數的幅值，Hm表示建立的數學傳遞模型的頻響函數的理論幅值。

2.2 模型的仿真和優化

針對上述2個人-椅傳遞模型，Matlab[9]和Isight聯合仿真，如圖6所示。

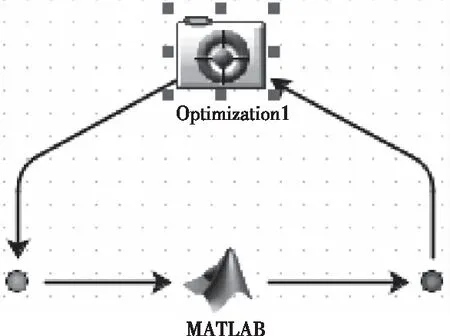
圖6 聯合仿真模型

為使參數表達式J取得最小值構建最優目標函數，選用Multi_islandGA算法[10]進行參數識別，其中各個參數初值取給定區間范圍的中間值。MATLAB負責接收各參數值并計算目標函數值，ISIGHT模塊[11]負責對目標函數進行評判和產生新的參數值，將獲得的所有目標函數值進行比較，選擇最小的J對應的未知參數，從而完成對目標函數的識別。用曲線擬合優度ε，式(6)來評價上述兩個模型擬合的優劣，最終的到完整的傳遞模型。

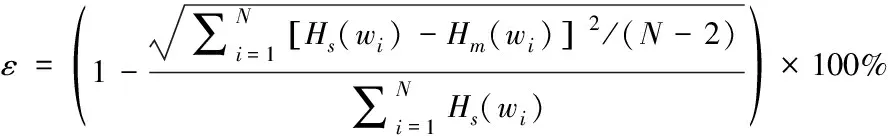
(6)

結合人體質量分布的實際情況，各個待識別參數的取值[12]范圍如式(7)和(8)，在該圍內擬合以求快速收斂。

針對3自由度模型為

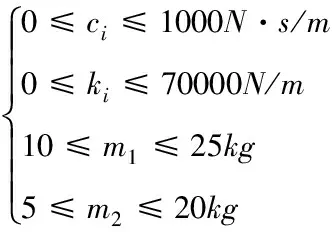
(7)

針對4自由度模型為

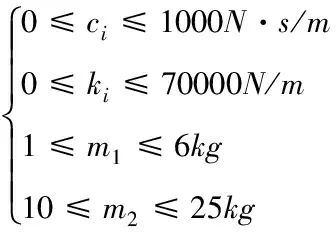
(8)

式中i=1，2，3，4。

其中3自由度模型的初值及運行結果如圖7所示。

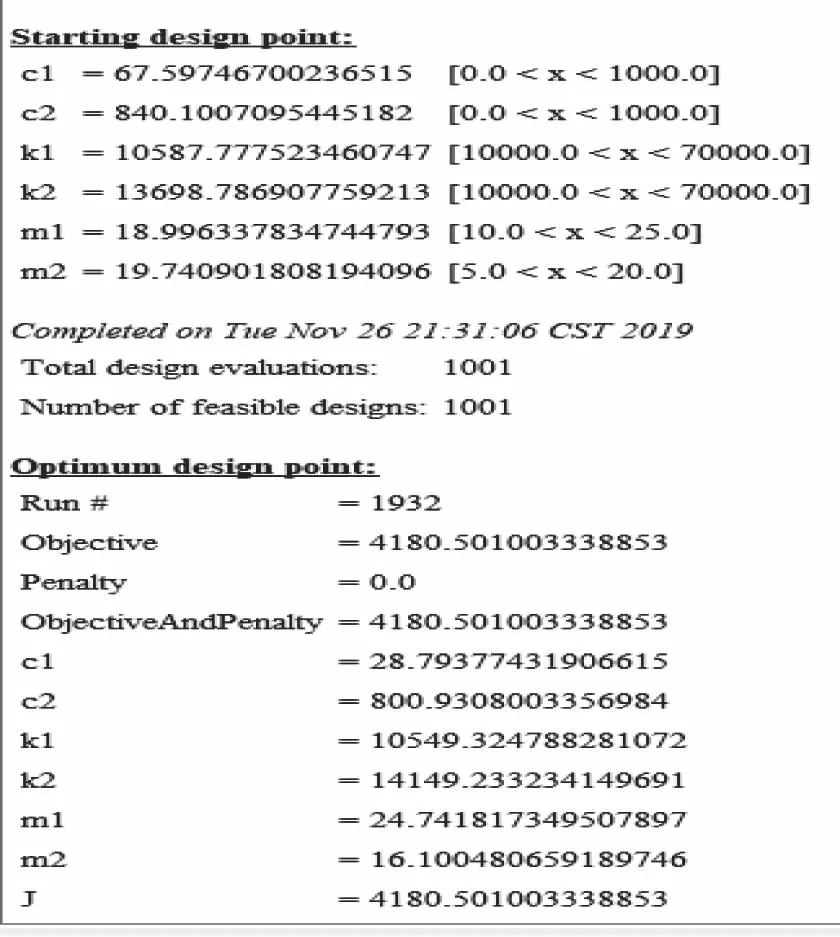
圖7 三自由度仿真結果

將3自由度和4自由度傳遞模型在Simulink中進行模型搭建如圖8和圖9。

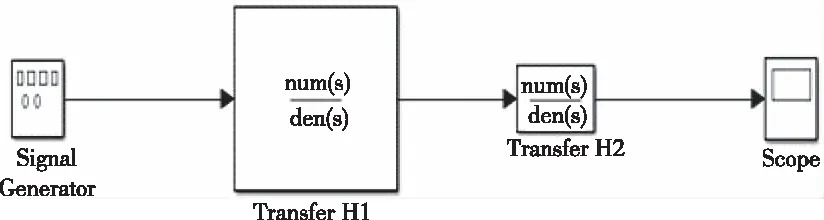
圖8 三自由度模型

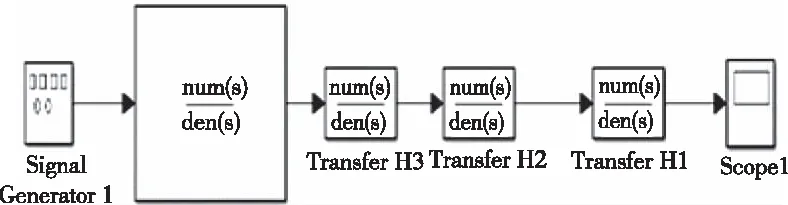
圖9 四自由度模型

根據聯合仿真得到各參數的具體取值如表1和表2所示

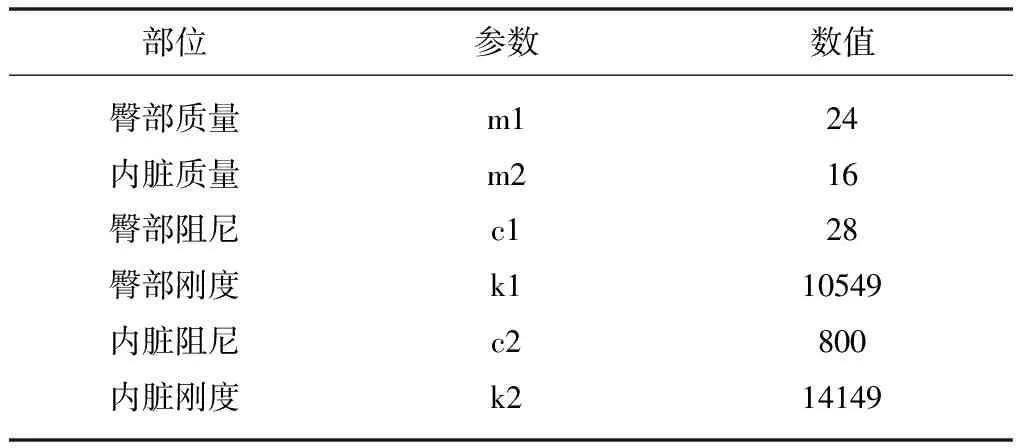
表1 三自由度模型參數

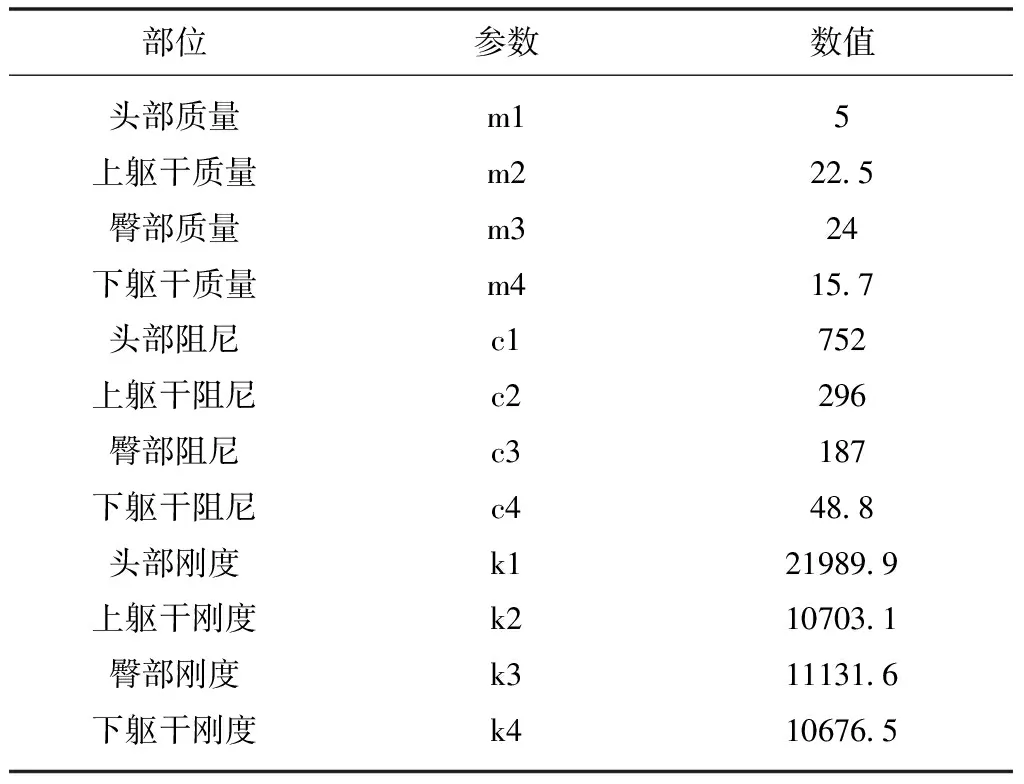
表2 四自由度模型參數

其中圖10為三自由度模型部分參數取值的二維分布情形，圖11為三自由度部分參數取值的三維分布情形，可以看出目標函數值逐步趨于收斂。

圖10 參數二維分布

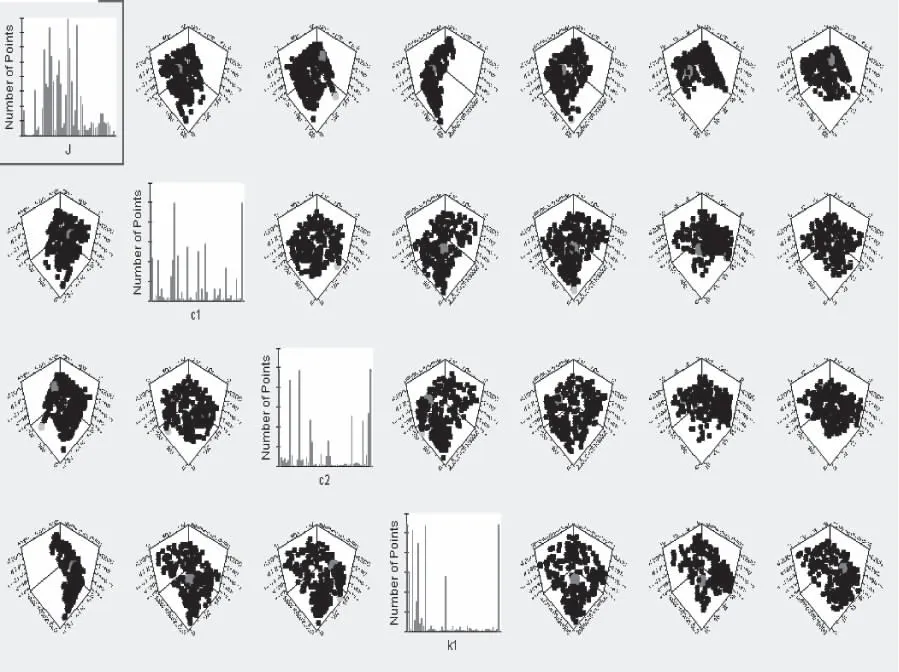
圖11 參數三維分布

通過聯合仿真確定出兩個傳遞模型的系統參數，為比較兩模型擬合的優劣，利用曲線擬合優度ε評價兩模型，得到ε分別為99.57%和99.63%，誤差值J1>J2，因此，理論上應選用模型2作為完整的傳遞模型；從實際情況來看，模型2較模型1相比復雜度增加，而擬合效果改善并不顯著，且模型1基本可以滿足實踐需求，綜合考慮選取模型1作為人體—座椅加速度傳遞模型。

3 結論

本文運用最小二乘法對仿真數據進行擬合，采用聯合仿真對模型優化完成參數識別，利用擬合優度ε型進行評價從而得出完整的人椅傳遞模型，在游樂設施人體加速度測試過程中，可以在僅知道座椅加速度的條件下通過模型響應關系，判斷人體加速度是否滿足安全判定要求。由于采用設備加速度作為人體加速度，不能準確的分析設備和人體相互作用帶來的加速度差異，本文模型可在僅知座椅加速度的條件下，依據模型傳遞關系獲取人體加速度并進而判斷是否滿足安全標準，為解決游樂設施運行過程中人體模型特定部位加速度測量難的問題，提供了新的途徑，有利于開展更趨合理的游樂設施乘載量化安全評價。