基于FFT和黃金分割的快速DOA估計
馮 成,龔曉峰,雒瑞森
(四川大學電氣信息學院,四川 成都 610065)
1 引言
陣列信號處理[1]中的空間譜算法可實現波達角精確估計,一直以來是學者們研究的熱點。測向技術主要有相關干涉儀測向[2],TDOA時間差測向[3],MUSIC類算法[4]和ESPRIT類算法[5]。其中,MUSIC 算法因分辨率高、穩定性良好,具有普遍的適用性,工程應用最為廣泛。
MUSIC算法是利用噪聲空間與信號空間的正交性實現對信號入射角估計。因其需要矩陣特征分解,譜函數計算和峰值搜索,涉及大量的復數運算,使得人們在應用MUSIC算法的過程中不得不增大掃描步進以減少算法計算量。
為降低MUSIC算法的運算復雜度,近來學者們提出了一些方法。文獻[6]利用子空間投影快速構建信號子空間,文獻[7]通過對一維均勻線陣的構造和重排得到等價噪聲子空間。 這些方法避免了矩陣的特征分解,而譜曲線計算的運算復雜度仍然很高。為此,文獻[8]通過變量代換將譜函數對應的復系數多項式轉換為實系數進行求根,從而減少求根所需計算量。文獻[9]利用部分噪聲子空間進行變步進譜峰搜索。文獻[10]提出先通過快速傅里葉變換(FFT)實現波束成形預估角度范圍,進而在預測范圍內用傳統MUSIC方法進行步進掃描,從而避免了全空域的譜峰搜索。更進一步的,文獻[11]在FFT變換預估角度的基礎上,通過線性調頻變換來計算譜函數值。然而,這些算法對計算量降低效果有限,復雜無線電環境下預估角度不準,導致測向失敗率上升。并且,各種已有改進算法的核心思想依舊局限在步進掃描和峰值比較的思路中。
MUSIC算法譜峰搜索的關鍵在于尋找譜函數極值點對應的角度值,這促使作者思考從迭代求極值的角度出發,選取合適的目標函數,經多次迭代使自變量收斂至極值點,從而完成DOA估計。黃金分割法可有效求解任意函數的極值點,然而,它需要合適的搜索區間作為迭代初始值。文獻[10-11]用FFT預處理信號向量陣得到角度預估范圍的方法在信號夾角變小時會失效,本文在此基礎上提出先對噪聲陣列向量補0,再FFT變換、各列變換值累加的方法以提高角度預估分辨能力。本文提出的結合FFT和黃金分割的快速DOA估計算法,首先,可以靈活選擇FFT變換點數調整角度預估能力,適應各種場景。其次,以構造的偽譜函數為目標函數做黃金分割,用利用迭代收斂快速精確的求解波達角,從而在保證精度的前提下避免了步進掃描繁冗的計算。而且,隨著天線陣列數和信號數的增加,算法復雜度只會略微增加。
2 陣列信號模型和MUSIC算法原理
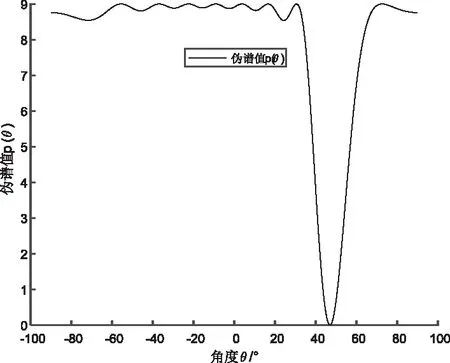
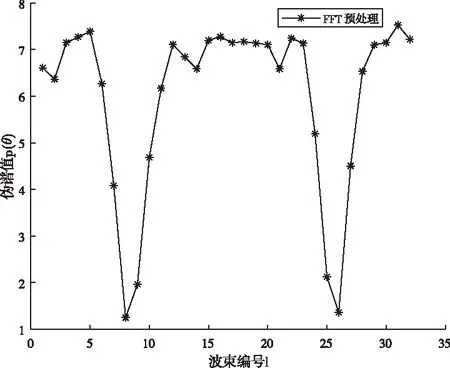
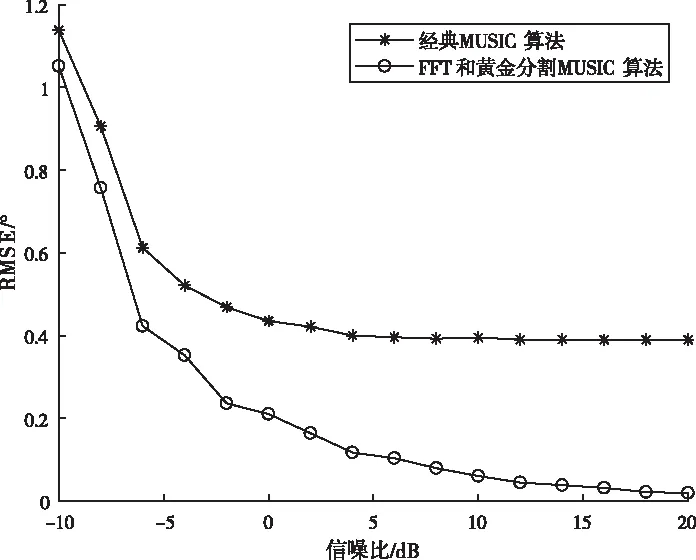
波長為λ,互不相干的M(M X(k)=A(θ)S(k)+N(k) (1) 其中A(θ)=[a(θ1),a(θ2),…,a(θN)]是陣列導向矢量矩陣[12],S(k)是入射信號,是噪聲信號。均勻直線陣的方向響應向量a(θi)如式(2) (2) 其中λ是入射信號中心波長,d是陣元間距,θi是信號與法線的夾角。 陣列接受數據的協方差矩陣記為Rxx,經Jacobi旋轉[13]或QR算法[14]特征分解得到信號子空間Us和噪聲子空間Un,如式(3)所示 Rxx=E[X(k)X(k)H]=UΣUH (3) 其中Σs是信號特征值構成的對角陣,Σn是噪聲特征值構成的對角陣。MUSIC算法指出陣列方向響應向量和噪聲子空間正交,既 a(θi)Un=0;i=1,2,…,M (4) 實際數據受噪聲影響,上式不精確為0。故取矩陣乘法后的向量模值的倒數,再取對數為譜函數值,如式(5-6)所示。譜曲線峰值所對應的角度便是來波方向的估計值。 (5) Pmusic=-10log10(c2+d2) (6) 若用經典MUSIC算法完成譜曲線計算,以9元直線陣為例,[-90° 90°]范圍內以1°為掃描步進,式(5-6)合計需要180*3次三角函數計算,180*91次復數乘法,180*80次復數加法,180次對數運算。至于圓陣,因需要在[0° 360°]范圍掃描,計算量翻倍。當陣元數N增加或者需要更高精度時,計算量也會成倍增加。可見降低運算復雜度對MUSIC算法十分重要。當然,若增大掃描步進,計算量將降低相應倍數,但同時犧牲了測向精度,這也是工程應用中常采用的折中辦法。 本文所提算法旨在提高測向精度的同時降低MUSIC算法的運算復雜度。基于FFT和黃金分割的MUSIC算法分為兩步:首先,用FFT變換預處理噪聲向量矩陣,得到角度預估范圍;然后,以預估的角度范圍作為迭代初始值,用黃金分割法求預估范圍內的偽譜函數極小值點,即為波達角的精確估計值。 空間譜估計的核心思想在于陣列導向矢量a(θ)與噪聲向量Un的正交性,兩者向量點積的模值應當接近0。構造偽譜函數P(θ)如式(7)所示 (7) 其中R為噪聲向量陣的總列數。均勻直線陣的導向矢量a(θ)具有范德蒙結構,將式(2)帶入化簡式(7)可得 (8) 其中Ui(n)為噪聲向量陣的第i列,第n行對應的元素。令f=-dsinθ/λ,代入式(8)有 (9) 易發現式(9)中含有Ui的離散傅里葉變換(DFT)的表達形式,使得可以考慮用快速傅里葉變換(FFT)計算式(9)在一系列指定f值對應的偽譜值。為此,需要將相位均分,令f=l/N,代入式(9)有 (10) 用FFT變換得到的N個偽譜值點,相當于將[-90° 90°]的空域范圍分成了N個波束,其中第l個波束對應的中心角度θl為 (11) 這里需要特別指明:當l的增加使反三角函數的自變量超出定義值時,需要先根據傅里葉變換的周期性對相位進行折算,再代入反三角函數。此外,N的取值不一定非得選擇天線陣元個數,根據FFT的數學定義可知,可以在噪聲列向量后添加任意個0,再取FFT變換以提高此預估方法的分辨率。因添加的是0值,故這只需付出極少的計算代價。 雖然相鄰兩波束的相移量是等間隔的,但每個波束的中心指向卻是不等間隔。表1給出了做32點FFT變換,d=λ/2時,用本文所提方法預處理噪聲向量陣時各波束對應的子空域角度值。 表1 各波束對應空域角度 比較FFT得到的偽譜值的大小,若某個譜值同時小于其兩側的譜值,且相鄰譜值差的絕對值大于2(篩掉假極小值點),則認為其對應角度θl是波達角的粗略估計值,選取其相鄰兩點對應的角度值作為下一步精確估計DOA的搜索范圍。 以一個信號源,入射角47°為例,圖1是對噪聲向量陣分別做16點和32點FFT變換所得的一系列偽譜值對比。理論分析和仿真都表明不同點數的FFT變換相當于對空域做不同比例的均分,可以看做是偽譜函數p(θ)在不同采用率下得到的一系列采樣點。對于32點FFT,20號點是符合條件的極小值點,查表格1知應選取[43.43° 54.34°]作為下一步黃金分割的搜索范圍。 圖1 FFT預處理所得的偽譜值曲線 黃金分割法是建立在區間消去法基礎上的試探方法,對函數f(x)在搜索區間[ab]內適當插入兩點x0和x1,如式(10-11)所示。計算對應函數值f(x0)和f(x1),如圖2所示。比較兩者大小,按式(12-13)更新區間。 x0=0.382*(b-a) (12) x1=0.618*(b-a) (13) iff(x0)>=f(x1);a=x0;b=b; (14) iff(x0) (15) 完成一次計算后,以新區間[ab]進行下一次黃金分割點插值,如此多次迭代,直到滿足條件b-a<ε(ε是一個預設的較小值)時,退出迭代,并取x=(a+b)/2作為極小值點的估計值。 圖2 黃金分割法示意圖 本文將偽譜函數p(θ)做為黃金分割的目標函數,則波達角是使p(θ)取接近0值的極小值點,FFT預處理噪聲陣的預估角度范圍是迭代初始值,多次迭代后,自變量θ便會收斂至波達角的精確估計值。選取p(θ)做黃金分割的目標函數是因為其極小值是接近0的值,可以輔助驗證極值點求解的正確性。另外,相比選擇傳統的譜函數值,如式(6)的Pmusic(θ),可以避免一些不必要的對數運算。 由2.1節中的示例信號繪制的p(θ)曲線如圖3所示,上一節預估的角度范圍[43.43° 54.34°]是迭代初始值,取ε=0.001,MATLAB仿真有:黃金分割法經15次迭代后,θ收斂至47.0092°。這說明了本文算法的正確性。 圖3 偽譜函數曲線圖 本節重點從理論上對比分析經典MUSIC和本文所提MUSIC算法的計算量。當天線陣元數取9,FFT變換點數取32時,兩種方法的譜峰搜索模塊對應計算量匯總于表格2。 表2 計算復雜度對比 其中K表示經典MUSIC需要計算的譜函數點數,取決于掃描精度。I表示黃金分割的迭代次數,后文仿真結果可知,黃金分割MUSIC求單個極值點的迭代次數總是迭代15次左右后收斂,遠遠小于傳統譜峰搜索方法需要計算的譜值點數K。80次復數乘法和160次復數加法是32點FFT變換所需計算量。 從表格1可直觀的對比出本文的新型DOA算法與經典MUSIC算法的運算復雜度比值近似為(I+1)/K。I的大小依賴于信號源個數m,因為m個信源意味著m次黃金分割,可以認為I=15*m。而用經典MUSIC的方法以1°為步進掃描直線陣對應的空域[-90° 90°],需要掃描180個點,即取K=180。有m=1時,新算法復雜度只有經典MUSIC的8.89%,m=2時,計算復雜度是原方法的17.22%。 綜上,改進算法先通過FFT變換快速計算一系列特定角度點對應的偽譜值,預估出角度范圍,再利用黃金分割迭代逼近DOA。避免了全空域的譜函數值的計算,而且完全規避了峰值搜索過程,計算量大幅度減少的同時還可以提高測向精度。 本節通過MATLAB仿真驗證所提算法的準確性和收斂性。仿真參數設置如下:均勻直線陣陣元數N=9,陣元間距d=0.5λ,快拍數n=1024,噪聲是加性高斯白噪聲,FFT變換點數選取32,黃金分割法退出迭代的預設閥值ε=10-3。 實驗1:選定兩個信號以±27.5°入射,信噪比snr=10dB,圖4是本文所提的FFT變換預處理噪聲向量陣而得的一系列偽譜值。通過比較此32個偽譜值大小,可得7號點和25號點是符合條件的極小值點,查表格1知,應選取[-30°-22.02°]和[22.02° 30°]作為角度預估范圍。 圖4 實驗1 FFT預處理 圖5是根據式(7)繪制的偽譜值函數P(θ)與角度θ的函數曲線圖,即黃金分割法的目標函數。 圖5 實驗1偽譜函數曲線 圖6 實驗2 FFT預處理 實驗2:增加信號源數量,減小入射信號夾角,降低信噪比。選定3個信號源以(-47.5°,42°,63.5°)入射,信噪比snr=0dB。圖6為FFT預處理得到的曲線圖,圖7是偽譜值P(θ)與角度θ的函數曲線圖。用相同的方法選取極小值點和查表1選取角度搜索范圍。 圖7 實驗2偽譜函數曲線 MUSIC算法改進前后,兩次實驗的估計角度θ,仿真時間T(僅指從噪聲子空間到DOA估計的計算時間)匯總于表格3。實驗顯示黃金分割法迭代15次左右收斂,驗證了之前的復雜度分析,相應仿真時間也降低至預計值。 表3 MUSIC改進前后DOA精度仿真時間對比 實驗3:為了比較算法改進前后的DOA精度做均方根(RMSE)誤差實驗[15],均方根誤差計算如式(13)所示 (16) 其中θi為波達角預設值,i為算法估計值,num為獨立仿真次數。實驗選取兩個信號源,分別在[-70°-20°]和[20° 70°]范圍內取隨機角度入射9元直線陣,信噪比范圍為[-10dB 20dB],步進為2dB。不同信噪比下獨立仿真100次計算均方根誤差。 圖8給出了經典MUSIC算法和黃金分割MUSIC算法的均方根誤差隨信噪比變化的曲線。由圖可得,在信噪比低端兩者DOA估計精度略有差距,隨著信噪比的提高,新型DOA估計算法的RMSE明顯小于以1°為步徑的傳統MUSIC算法,此時迭代達到了更高精度掃描的效果。 圖8 兩種方法估計精度對比 從理論上分析,由于噪聲子空間的構造方式一致,所以經典MUSIC算法與基于FFT和黃金分割的MUSIC算法對應譜函數的極值點也應該一致,差異在于本文所提算法是用黃金分割法迭代逼近極值點,從而使得在計算復雜度降低的情況下,測向精度反而提升。 本文以降低MUSIC算法譜峰搜索模塊運算復雜度為目的,提出一種結合FFT和黃金分割的快速DOA估計算法,解決工程實踐在測向精度和實時性兩者間做取舍的困境。改進DOA算法主要優點有:1:譜函數模塊的運算復雜度降低至經典方法的17%左右;2:改進算法測向精度比1°步徑掃描的經典MUSIC算法更高;3:在多個信號源同時存在,低信噪比下也能成功預估角度并實時測向;4:改進算法將迭代求極值的思想引入以規避傳統方法的峰值搜索,為無線電信號處理提供了一些新的數學思路。黃金分割法并不依賴于特定的天線陣列形狀,而FFT預處理噪聲陣的方法卻只適用于均勻直線陣,尋求復雜無線電環境下任意陣列形狀的角度預估方法和更加精簡的迭代算法是迭代求解波達角的下一步研究方向。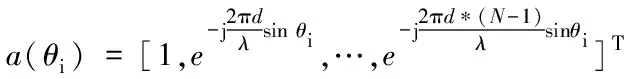
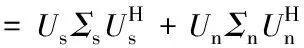

3 基于FFT和黃金分割的新型DOA
3.1 FFT粗估計DOA







3.2 黃金分割法精確估計DOA

4 算法復雜度分析

5 仿真驗證





6 結束語

