基于MARKOV隨機信道分配的車隊控制研究

喬 棟，謝亞龍，賈 權，姚 濤

(1.山西大同大學建筑與測繪工程學院，山西大同 037009;2.山西大同大學煤炭工程學院，山西大同 037009;3.山西大同大學機電工程學院，山西大同 037009;4.河北工業大學機械工程學院，天津 300401)

1 引言

隨著汽車保有量急劇增加和智能交通的發展，交通擁堵不僅僅是一、二線城市具有的城市病，三、四線城市也出現了不同程度的交通擁堵現象，尤其是在中國，交通擁堵以及由汽車尾氣所造成的環境污染已然成為急需解決的城市病。僅僅通過增加道路通行能力和從車輛性能方面入手，并不能很好的解決上述問題，且治標不治本。采用先進的高科技手段，即智能交通系統(Intelligent Transportation System)，成為上述問題的新思路[1-2]。

自主車隊控制系統[3]作為智能交通系統未來的發展方向，是指公路系統中的車輛按照期望的隊形組成車隊行駛。通過車載雷達傳感器[4]、超聲波[5]、攝像頭[6]等裝置提升舒適度與安全性，但容易受到外界因素的影響，例如霧霾、大雨等。近些年，網絡通信技術飛速發展[7-11]，將無線通信技術應用到自主車隊控制系統中，能夠有效的解決上述問題。V2V[12]V2I[13]成為必然趨勢。無線通訊網絡的介入，必然會帶來網絡的固有缺陷，例如延時、丟包、亂序和介質訪問約束等。而且車輛的快速移動性，使得網絡化車隊控制系統有別于傳統的網絡控制系統，給研究人員帶來了巨大的挑戰，但是其應用前景廣闊。

在國內，主要是Guo的團隊對網絡化自主車隊進行研究[14-15]。而且對于網絡車隊控制系統的研究主要集中在通信時延方面。文獻[16]通過狀態估計和線性矩陣不等式方法獲得了車輛間數據的最大丟包數。而文獻[17]則是從一致性的角度出發，研究了車輛間的通信時延問題。目前大多數的研究都是基于單一網絡因素對車隊控制性能的影響，而文獻[18]則是綜合考慮了通信時延、丟包、亂序和數據包異步問題，構建了離散度車隊數學模型，通過智能處理器保證車隊穩定。車輛數量的急劇增加，使得網絡化車隊控制系統中的信道受限問題不可避免。文獻[19]通過動態調度與靜態調度結合的方法，給出了車輛間通信調度序列與控制器協同式設計方法。上述研究所獲得的調度序列是基于時間調度的，而網絡信道的分配是由事件驅動的(包括確定事件與隨機事件)，確定事件類似與時間驅動。

本文主要研究了隨機事件，即車輛間通信信道的分配是隨機的，對于信道隨機分配的網絡化車隊控制系統，基于調度的方法已不再使用。而且目前對于車隊信道受限的研究主要集中在調度方向。

基于上述討論，本文主要通過將車輛間通信信道的隨機分配特性描述為轉移概率部分未知的Markov模型，然后將異構網絡化車隊模型建模為多個狀態的Markov跳躍系統，并給出了車隊控制系統隨機穩定的條件以及相應控制器的設計方法，最后通過仿真與實驗驗證了其有效性和實用性。

2 網絡化自主車隊建模

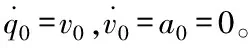
圖1 異構網絡化車隊模型

2.1 網絡化車隊建模

跟隨車輛i(i=1，2，…，N)的縱向動態模型表述為[15]：

其中，qi、vi和ai分別表示第i輛車的位置速度和加速度。ci是發動機的輸入

其中，dmi、cdi、Ai、mi和σ分別表示第i車的拽力系數、機械阻力、橫截面面積、質量和空氣質量密度，σAicdi/2mi代表空氣阻力，ηi是發動機的時間常數。通過反饋線性化方法，對上述非線性車輛模型進行控制器設計，則

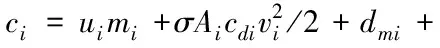
其中，ui是車輛i控制輸入量。因此，車輛的近似動力傳動系統表示：

(1)

為每一輛跟隨車輛i設計合適的控制律ui，實現以下跟蹤性能，

qi→q0+Li+di，0；vi→v0；ai→ 0

(2)

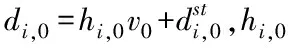
β[vi(t)-v0]-γ[ai(t)-a0]-

(3)

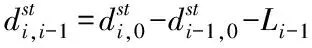
分別定義車輛i與領頭車的位置、速度和加速誤差信號

(4)

因此，可用下式表述第i輛車的分布式控制策略

ui(t)=-β[vi(t)-v0]-γ[ai(t)-a0]-

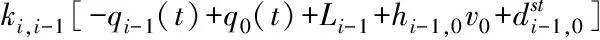
(5)

通過數學變換，可得第i輛車的分布式控制策略

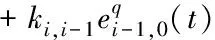
(6)

因此，可獲得第i輛車的誤差模型

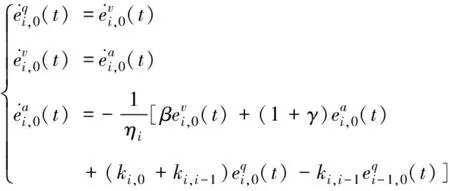
(7)

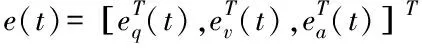
u(t)=(-k1-k2+k2C)e(t)

其中

k1=diag{k1，0，k2，0，…，kN，0，β，…，β，γ，…，γ}∈R3N×3N，

k2=diag{k1，0，k2，1，…，kN，N-1，0，…，0}∈R3N×3N

因此，基于無線網絡通信的異構網絡化車隊控制系統為

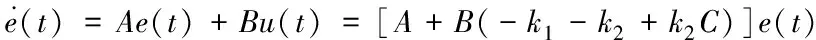
(8)

其中

η=diag{η1，η2，…，ηN}

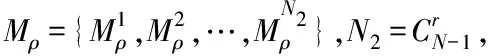
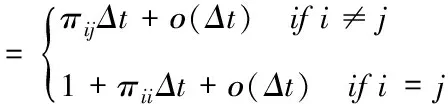
(9)

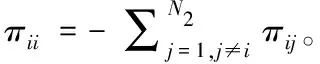
本文研究的是用于描述通訊信道的Markov過程的轉移速率部分未知情形，即轉移速率矩陣π=[πij]的元素部分未知。比如Markov有四個工作狀態，則其對應的轉移速率矩陣為

在t時刻，基于信道受限的控制策略為

u(t)=(-k1-Mρ(t)k2+Mρ(t)k2C)e(t)

(10)

因此，基于通信受限的網絡化車隊控制系統模型為

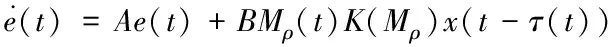
(11)

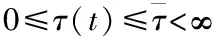
2.2 控制目標

為了獲得期望的車間距，需要為跟隨車輛設計控制器(3)，使得整個異構網絡化車隊控制系統滿足如下性能：

1)車隊穩定性：異構網絡化車隊控制系統隨機穩定；

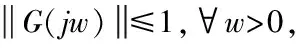
3 車隊穩定性分析

3.1 車輛隨機穩定性分析

在上一小節，得到了基于通訊信道受限的異構網絡化車隊模型(11)。在本小節通過以下定理能夠保證跟隨車輛隨機穩定，而且也給出了對應控制器的設計方法。

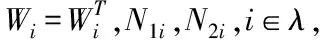
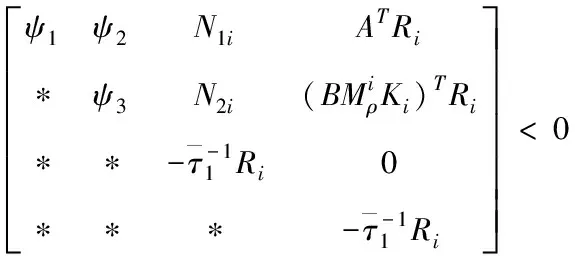
(12)

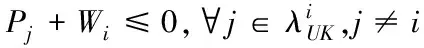
(13)

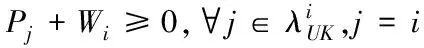
(14)

那么車隊控制系統(11)隨機穩定。其中

證明：定義Lyapunov-Krasovskii泛函

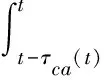
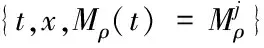
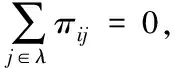
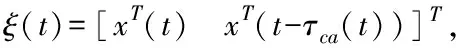
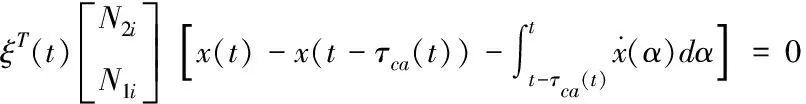
進而可知

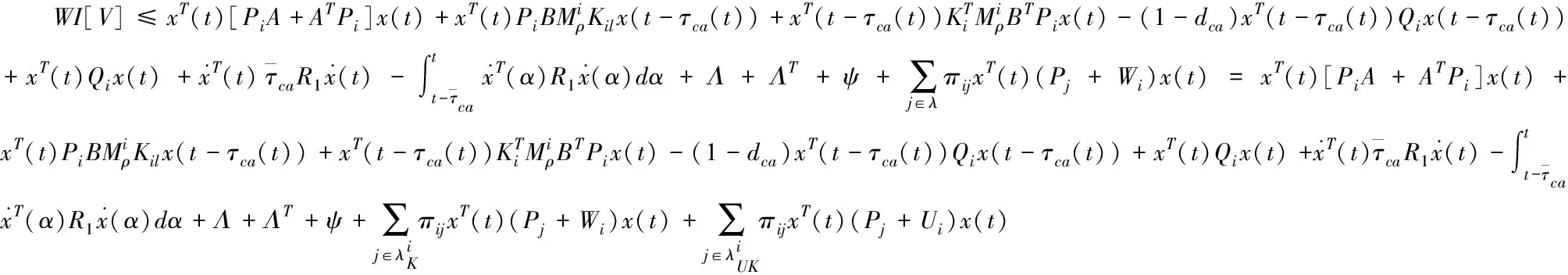
(15)

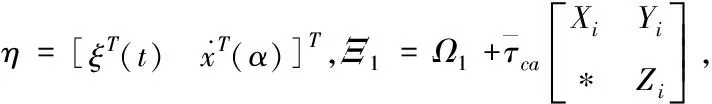
當i，j∈λ，j≠i時，πii<0且πij>0成立。結合(15)可知：如果

Ξ1+Ξ2<0

(16)

Θ≥0

(17)

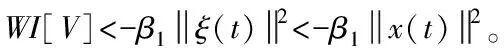
Pi>0由Schur補引理[18]可知，(17)等價于

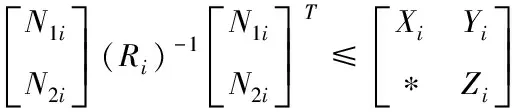
(18)

結合(16)，(18)和Schur補引理，可得(12)，證畢。

定理1給出了車輛隨機穩定的理論依據。可通過如下定理求得對應控制器增益。

(19)

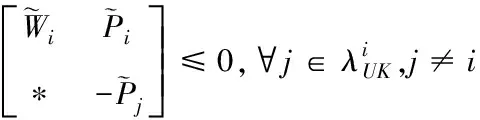
(20)

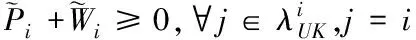
(21)

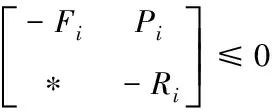
(22)

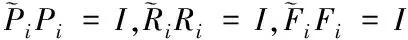
(23)

其中

相應的控制器增益為

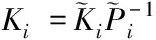
(24)

分別用矩陣J左乘和右乘(12)，并對其進行合同變換可得

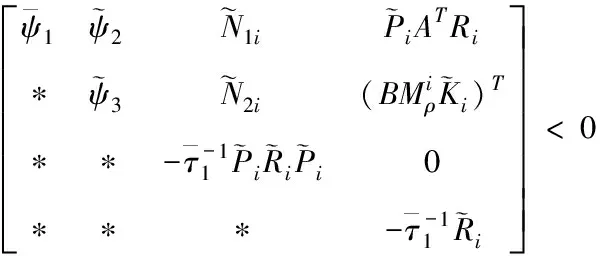
(25)

其中

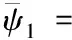
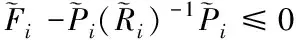
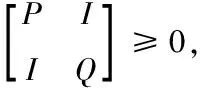
基于下列條件

最后根據文獻[20]中的算法1，即可求解該問題。

3.2 車隊隊列穩定性分析

上一小節，給出了保證車輛隨機穩定的條件以及對應控制器的設計方法，對于車隊控制，為了防止追尾事故的發生，還需要滿足車隊隊列穩定性，即車間距誤差沿著隊列向后逐漸遞減，最終趨近于0。

通過車輛的動態模型和控制律可得，車輛i的誤差方程

將式(1)和(3)帶入上式可得

ki，i-1ei，0+ki，i-1ei-1，0

(26)

對式(26)Laplace變換

(27)

對(27)進行頻域分析，可以通過以下定理保證車隊隊列穩定。

定理3：對于任意的w>0，|ei，0(jw)/ei-1，0(jw)|≤1成立，當且僅當以下條件

γ2-2βηi≥0

(28)

ki，0γ-ki，i-1γ≥0

(29)

成立，則達到車隊隊列穩定。

證明：為了保證車隊隊列穩定性，首先給出|ei，0(jw)/ei-1，0(jw)|為

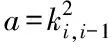
因為a>0，因此要使|ei，0(jw)/ei-1，0(jw)|≤1成立，只需b≥0 ，則車隊隊列穩定。如果(28)和(29)成立，則b≥0 成立，證畢。

本文所提出的控制律能夠保證車隊實現零穩態誤差。在t時刻，定義領頭車的速度與穩態速度v0的偏差為ε0(t)=v0(t)-v0，因此

(30)

通過式(30)和(1)可得

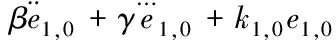
(31)

對式(31)Laplace變換，可得第一輛跟隨車輛與領頭車的車間距誤差變換關系

(32)

不失一般性，假設領頭車在有限時間tf內達到最終的穩態值，則當t≥tf時，ε0(t)-ε0(tf)=0成立。所以

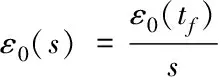
(33)

最后，通過使用終值定理和式(31)、(32)和(33)，可得

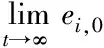
=0

其中，i=1，2，…，N。因此可以保證車隊的零穩態誤差。

3.3 車隊控制算法

下面給出整個異構網絡化車隊控制系統的算法過程。

算法1：

1)通過反饋線性化方法設計控制器(3)，該方式在傳統的非線性控制以及其它文獻中頻繁使用，本文給出，體現本文所設計控制算法的完整性。

2)根據定理2，利用LMI工具箱獲得整個車隊控制增益k1，k2；

3)檢驗所得的控制器增益k1和k2是否滿足隊列穩定性的條件(23)和(24)。如果滿足，則說明所獲得的控制器增益滿足車隊隊列穩定性要求。反之，需要重新設定相關矩陣，返回到第二步重新求解。

4 MATLAB仿真與實驗

本小節首先通過MATLAB仿真驗證了所提出算法的有效性，最后通過由Arduino小車所組成的車隊驗證了本文的實用性。

4.1 MATLAB仿真

通過MATLAB軟件搭建了由5輛車組成的網絡化車隊控制系統，并將本文所提出的算法應用到上述搭建的模型中。

假設領頭車初始速度為30m/s，且加速度滿足如下特性

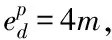
假設對應Markov的轉移速率矩陣為

其中‘？’代表未知的元素。信道隨機分配的狀態序列如圖2所示。

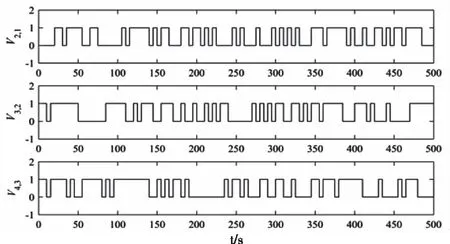
圖2 跟隨車輛與其直接前車的通信序列

通過定理3.2求得控制器增益為

k1=diag{ 1.2569， 1.1574， 1.0856， 1.0485，2.5815， 2.5815， 2.5815， 2.5815，2.1694， 2.1694， 2.1694， 2.1694}

k2=diag{ 3.6236， 1.69262， 2.6598， 2.1653，0， 0， 0， 0， 0， 0， 0， 0}

從圖3-5可以看出，對于信道受限的異構網絡化自主車隊控制系統，本文研究的算法能夠保證車隊隨機穩定，且整個車隊隊列穩定。

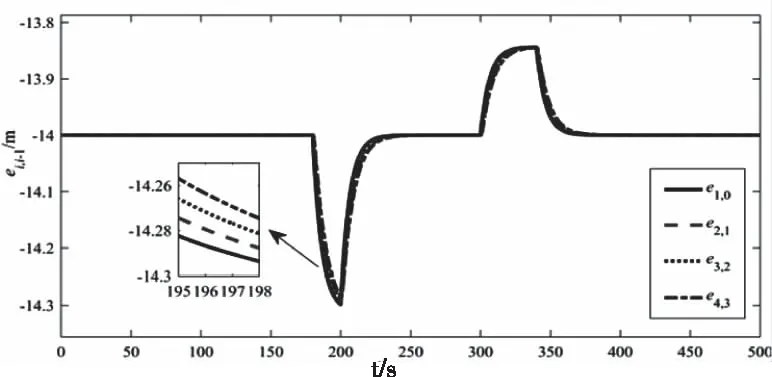
圖3 相鄰車輛的車間距誤差

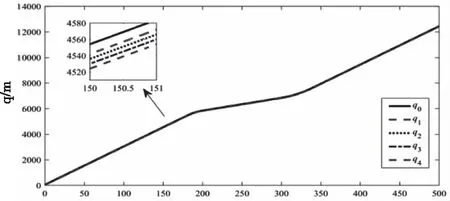
圖4 車輛的位置響應特性

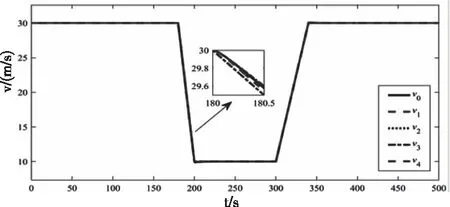
圖5 車輛的速度響應特性

4.2 Arduino車隊實驗

為了驗證本文算法的實用性，本小節通過4輛Arduino智能小車來模擬信道受限的異構自主車隊控制系統，如圖6和圖7。車輛間采用的無線模塊為APC220，工作頻率為418MHz到455MHz，傳輸距離為1000m。

圖6 Arduino小車

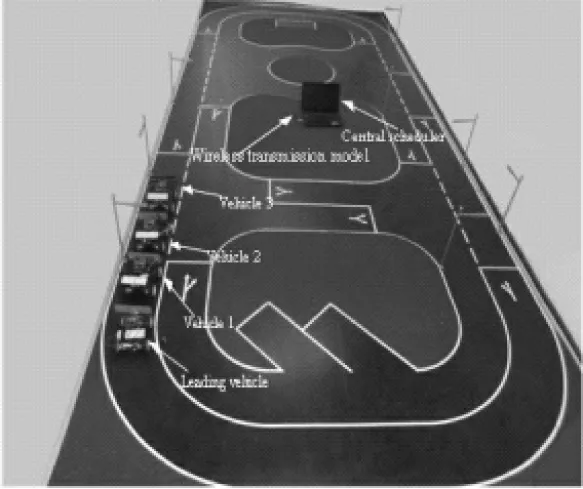
圖7 智能車隊

文所提出的算法，能夠使得跟隨車輛維持期望的車間距。

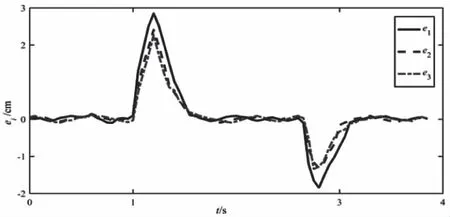
圖8 智能車隊車間距誤差響應特性

5 結論

本文研究了通訊信道受限的異構網絡化車隊控制系統，將通信信道建模為轉移概率部分未知的多狀態Markov跳躍模型，通過Lyapunov定理和LMI工具，獲得了車輛隨機穩定性條件以及對應控制器的設計方法，通過頻域分析給出了車隊隊列穩定性條件。最后通過MATLAB仿真和Arduino車隊實驗，驗證了本文所提出算法的有效性和實用性。

本文研究的是跟隨車輛與其直接前車通訊信道受限問題，與領頭車輛的通訊是不受限的。而跟隨車輛不僅與其直接前車的通訊受限，而且與領頭車輛的通訊也受限情形，作為將來的研究方向。