流固耦合作用下制動氣室動態特性建模與試驗

邵 瑜，朱茂桃

(江蘇大學汽車與交通工程學院，江蘇 鎮江 212013)

1 引言

由于氣壓制動的制動力矩大、操縱輕便，絕大部分載貨汽車及客車安裝氣壓制動系統[1-2]。制動氣室作為氣壓制動系統中的主要裝置，用于連接汽車制動回路與制動執行機構。制動氣室的壓力特性影響制動器的制動力輸出和制動性能[3]，而目前國內在制動氣室設計開發方面的研究較少，因此，研究制動氣室的動態特性對高性能氣壓制動系統的開發具有重要意義。

氣壓制動系統已經得到了廣泛的研究，許多學者建立了相應的模型預測制動腔內的瞬態壓力。周佳瑋等[4]根據制動氣室工作原理，建立制動氣室數學模型，在此基礎上采用AMESim軟件分析其在不同壓力源下的動態相應特性及推桿行程變化。朱薔等[5]依據氣體流動的狀態方程、連續性方程及動力學方程對制動氣室輸出壓力特性進行數學描述，并進行試驗驗證。李興麗等[6]通過對制動氣室的流量特性方程、狀態方程及活塞盤的運動方程無因次化，得到制動氣室無因次解析模型，并通過試驗進行驗證。

雖然上述學者們在制動氣室動態特性方面做了很多研究，但他們的研究主要是對其進行數學建模，缺乏對流體和固體之間相互耦合作用的考慮，誤差較大。本文基于流固耦合有限元分析的理論與方法，運用ADINA仿真軟件建立了制動氣室的流固耦合有限元模型，分析制動氣室在壓縮空氣作用下的動態特性，并與試驗結果對比，驗證了建模方法的正確性。文中對制動氣室的建模方法和試驗方法，可為實際產品的開發提供理論支持。

2 制動氣室結構及試驗方法

制動氣室的基本結構如圖1所示，主要由進氣口、橡膠膜片、殼體、回位彈簧、推桿、夾箍和螺栓等組成。橡膠膜片將氣室分成兩個腔室，當汽車制動時，壓縮空氣從進氣口進入制動氣室壓縮腔，在壓縮空氣的作用下使膜片發生變形，推動推桿，并帶動制動調整臂，將制動蹄摩擦片壓向制動鼓從而產生制動；當推桿達到極限位移時，制動氣室仍將持續沖入壓縮氣體，直至壓力達到最大；制動結束，制動氣室壓縮腔內的氣體通過快放閥釋放，在回位彈簧的作用下氣室壓縮腔的體積不斷減小，直至回歸原位。

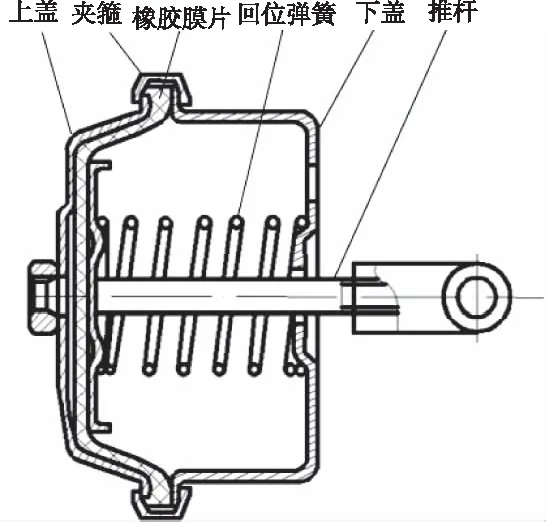
圖1 制動氣室結構圖

根據QCT790-2007《制動氣室性能要求及臺架試驗方法》，建立制動氣室實驗裝置，如圖2和圖3所示。壓縮機為制動系統提供壓縮空氣，可最大提供0.9 Mpa的壓縮空氣，與壓縮機集成一個容量為90公升的儲氣罐，并使用調壓閥調節儲氣罐輸出的壓力，壓縮空氣通過軟管輸送至制動氣室。壓力傳感器安裝在制動氣室前端蓋打孔處，用于測量壓縮腔內的空氣壓力變化情況。采用激光位移傳感器測得推桿的位移變化情況。所得到的電磁閥信號、制動氣室壓強信號、推桿位移信號通過數據采集儀，最終送達信號處理系統。

圖2 試驗現場圖

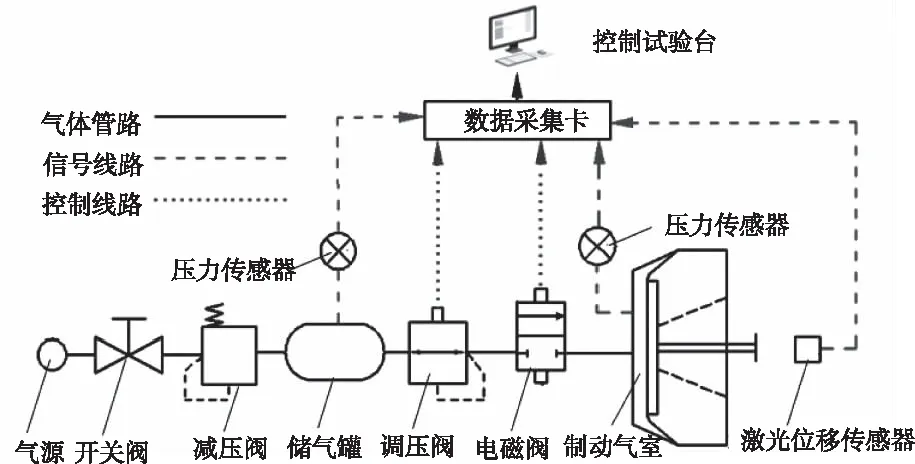
圖3 試驗系統布置圖

3 流固耦合理論

流固耦合運動過程中，結構在流體載荷的作用下發生運動，其變形進而改變流體載荷的大小和分布[7]。為分析壓縮空氣作用下制動氣室的動態響應，在流體-結構界面的運動學和動力學條件為[8]

df=ds

(1)

nτf=nτs

(2)

其中df和ds分別表示流體和結構的邊界位移，τf和τs分別表示流體和結構的邊界應力，n為耦合邊界上的外法線矢量。

根據動力條件，流體牽引力沿流體-結構界面整合成流體力，施加于結構節點上，其大小為

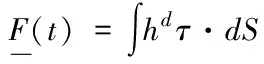
(3)

其中，hd表示固體位移的虛量。

耦合系統的解向量為X=(Xf，Xs)，其中Xf和Xs分別為分別定義在流體節點和固體節點上的流體和結構域的解向量。此時ds=ds(Xs)，τf=τf(Xf)。耦合流固耦合體系的有限元方程可以表示為

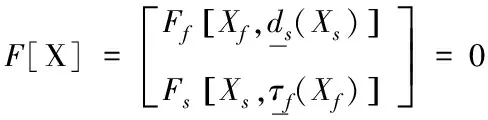
(4)

其中，Ff和Fs分別為流體和結構的流固耦合邊界上關于時間積分的有限元代數方程組。

運用ADINA軟件進行流固耦合計算，分別在ANDINA結構模塊和流體模塊中建立結構模型和流體模型，將兩個模型放入ADINA流固耦合求解器中進行求解。采用Newton-Raphson迭代算法對兩個模型進行耦合求解即對式(4)進行求解，得到流場和結構場的位移情況。

4 制動氣室流固耦合模型建立

4.1 有限元模型

由于結構和流體幾何模型均具有軸對稱特點，且載荷和邊界條件也具有軸對稱特點，因此將三維計算分析簡化成二維計算分析。同時建立結構幾何模型和流體幾何模型，在建立流固耦合計算模型時，在軟件結構模塊中劃分結構部分的網格，在軟件流體模塊中劃分流體部分的網格。

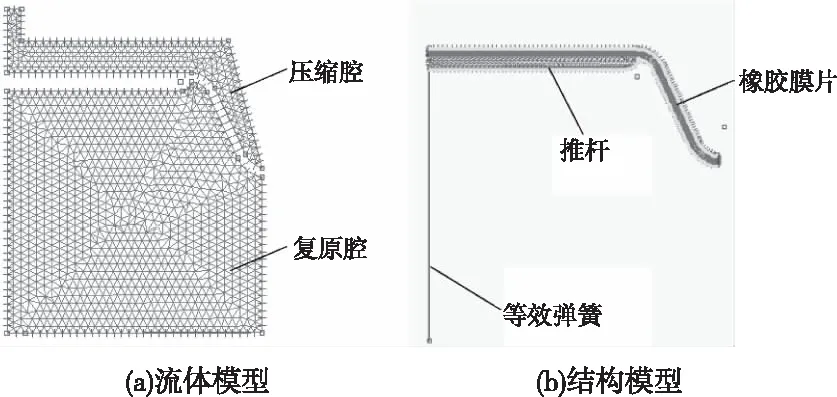
圖4 制動氣室流固耦合有限元模型

4.2 材料參數

流體區域的材料為空氣。流體的邊界是完全封閉，當施加進氣壓力時，流固耦合邊界發生變形，因此需要考慮空氣的可壓縮性。對于可壓縮流體模型，材料參數包括：粘度、等壓比熱、等容比熱、熱傳導系數、參考溫度。流體的密度是由與溫度和壓力相關的狀態方程計算，因此不考慮體積模量和密度[9]。

表1 流體材料參數

橡膠材料為超彈性材料，一般通過某種簡單的變形情況下的應力應變屬性描述橡膠力學性能。采用回歸分析，以一個適當的應變能函數實驗得到的應力應變數據進行擬合，并將擬合得到的有關數據作為有限元分析的輸入[10]。本文采用Ogden函數描述橡膠的力學性能，其多項式應變能函數為：

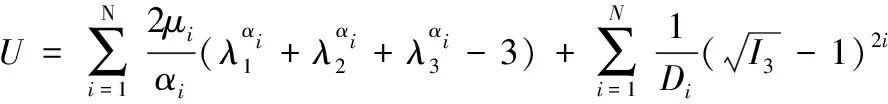
(5)

其中λ1、λ2、λ3是三個主拉伸比，μi、αi為由實驗數據決定的材料常數，Di為表征可壓縮性的體積模量。

采用GOTECH AI-7000 M拉伸試驗機對橡膠材料進行單軸拉伸、壓縮試驗，用于拉伸實驗的啞鈴形試片，其工作標線間距25±0.5 mm，工作部分寬度為6.0±0.4 mm，厚度為2.00±0.03 mm；用于壓縮實驗的圓柱形試塊，其直徑為29 mm，厚度為12.5 mm。表2為橡膠材料的應力應變數據，軟件可自動擬合應力應變數據，生成Ogden材料本構模型系數及體積模量，并繪制擬合曲線。

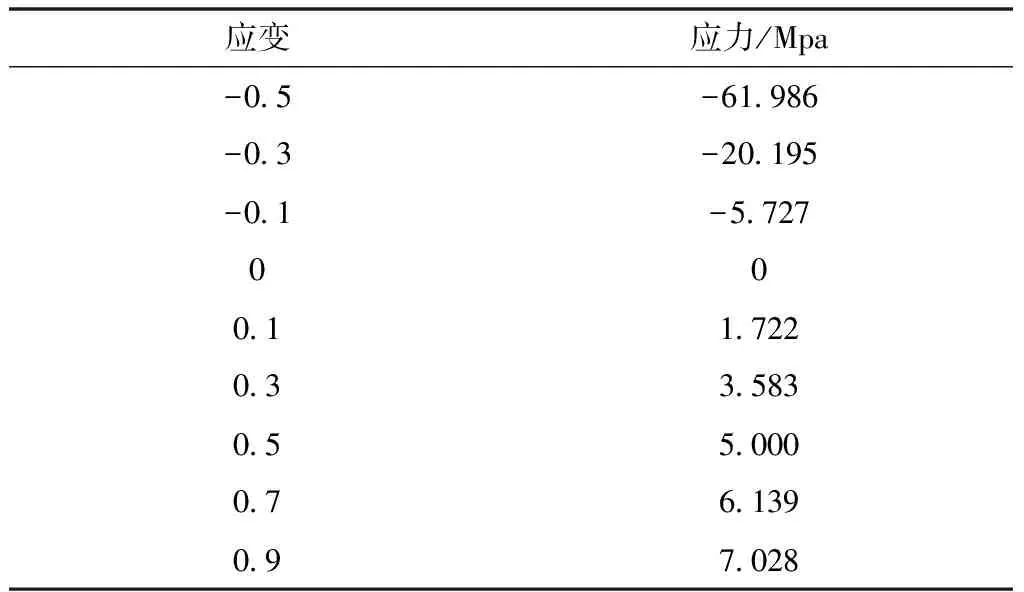
表2 橡膠材料應力應變數據

采用微機控制彈簧拉壓試驗機對芯軸回位彈簧進行壓縮試驗，每壓縮10 mm記錄一次負載值，彈簧的計算剛度偏差在5 %左右，假設芯軸回位彈簧為線性彈簧，取剛度的平均值為2.882 N/mm。

4.3 邊界條件

圖5為固體模型的邊界條件，對固體模型中的推桿施加由安裝過程中產生的彈簧預應力，并約束推盤除運動方向外所有的自由度，固體模型與流體模型中的流固耦合接觸面一一對應。對于軸對稱模型，不論是結構模型還是流體模型，對稱中心線可以不施加任何邊界，軟件可以識別對稱中心線并施加相應的約束邊界。

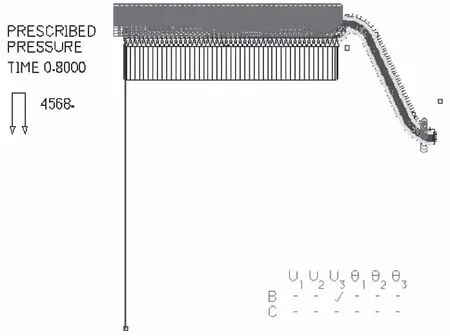
圖5 結構模型的邊界條件

對于可壓縮流體的流固耦合計算，流體的壓力、溫度和密度的初始條件必須滿足狀態方程，如下式

p=(cp-cv)ρθ

(6)

其中，p為流體初始壓力，pa；θ為流體溫度，K；ρ為流體初始密度，kg/m3。

圖6為流體模型的邊界條件，設置流體的初始壓強為0.1 Mpa，溫度為338 K。流體壁面定義為非滑移壁面，對進氣口施加壓力載荷。

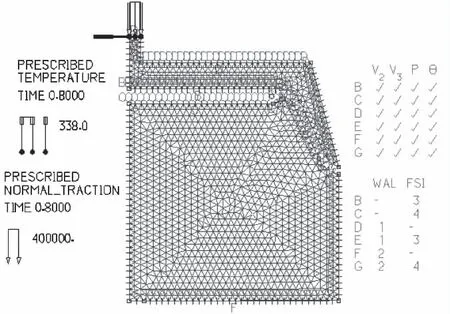
圖6 流體模型的邊界條件

流體模型采用Turbulent K-Epsilon 湍流模型，橡膠膜片上下表面設置為流固耦合接觸面， 結構仿真模型采用隱式計算方法，流體仿真模型采用瞬態仿真計算方法，耦合時間步設為1×10-5s。

5 制動氣室動態特性分析

5.1 制動氣室動態特性仿真與試驗結果對比

圖7和圖8為制動氣室在0.4 Mpa的進氣壓力下，制動氣室壓力曲線和推桿位移曲線。由圖7可知。制動氣室的運動可分為三個部分。運動初期，制動氣室內的壓強快速增加；達到0.1368 MPa時在壓強的作用下橡膠膜片發生變形，推動推桿進行運動，隨著推桿的運動，制動氣室內的體積快速增大，制動氣室內的壓強在一定范圍內發生波動；當推桿到達極限位置時，制動氣室的壓強迅速提高，直至最大。制動氣室在充氣過程中的計算結果與實驗結果的曲線總體趨勢一致，證明本文建模方法與計算方法的正確性。

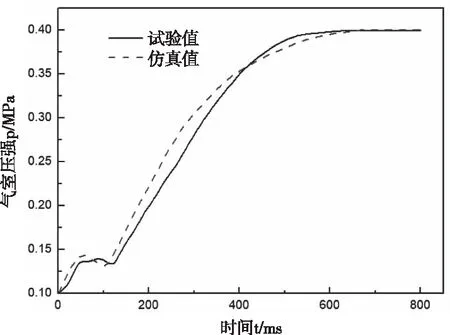
圖7 制動氣室壓強變化曲線

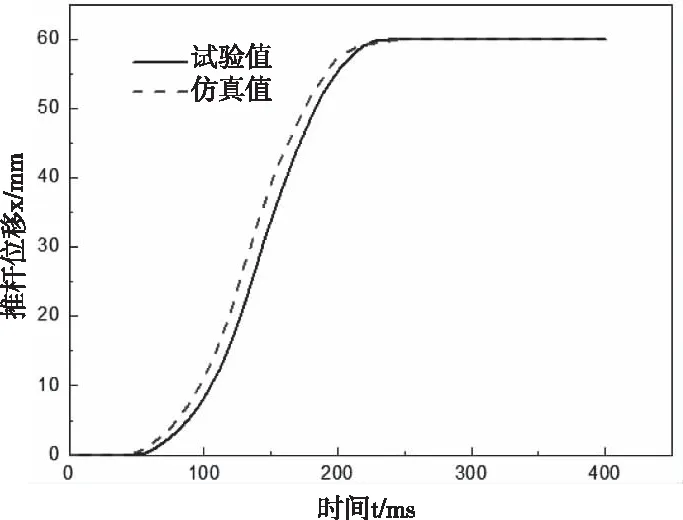
圖8 制動氣室推桿位移曲線

壓力響應時間為制動氣室的壓力達到穩態最大壓力值的75%時所經歷的時間，表3為制動氣室壓力響應時間情況，由表3可知，不同供氣壓力下制動氣室壓力響應時間的試驗值和計算值誤差均小于15 %，所見的計算模型精度較高。

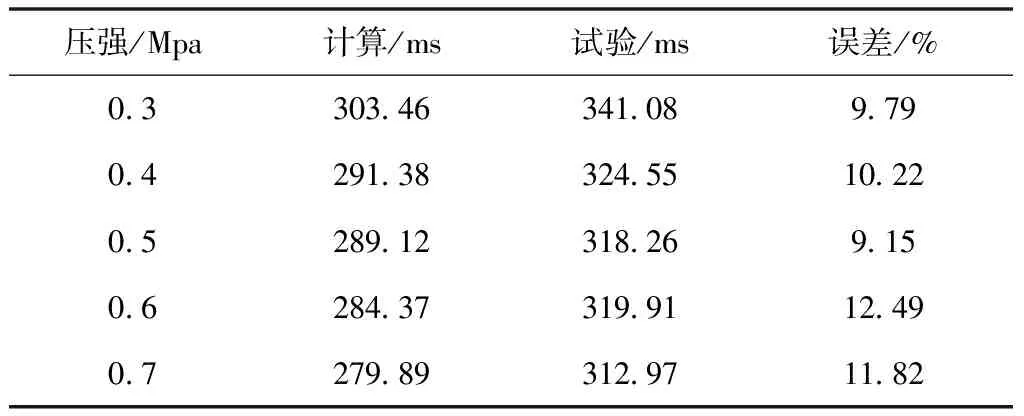
表3 制動氣室壓力響應時間計算值與試驗結果

5.2 制動氣室流場特性仿真結果

制動氣室內部流場試驗測試與理論分析較為困難，通過流固耦合有限元分析計算可以直觀地獲得制動氣室內部流場的分布情況，同時能掌握制動氣室結構變化對其性能的影響情況

圖10為不同推桿位移情況下制動氣室流場情況。從圖中可以看出：推桿位移從20 mm增加到60 mm，制動氣室的壓強變化不大，這是由于在壓縮空氣的作用下，制動氣室密封腔內的體積變大，橡膠膜片變形較復雜，制動氣室的壓強緩慢地增加。入口處流體壓力場急劇變化，壓力梯度大，在入口側存在小范圍地負壓區。

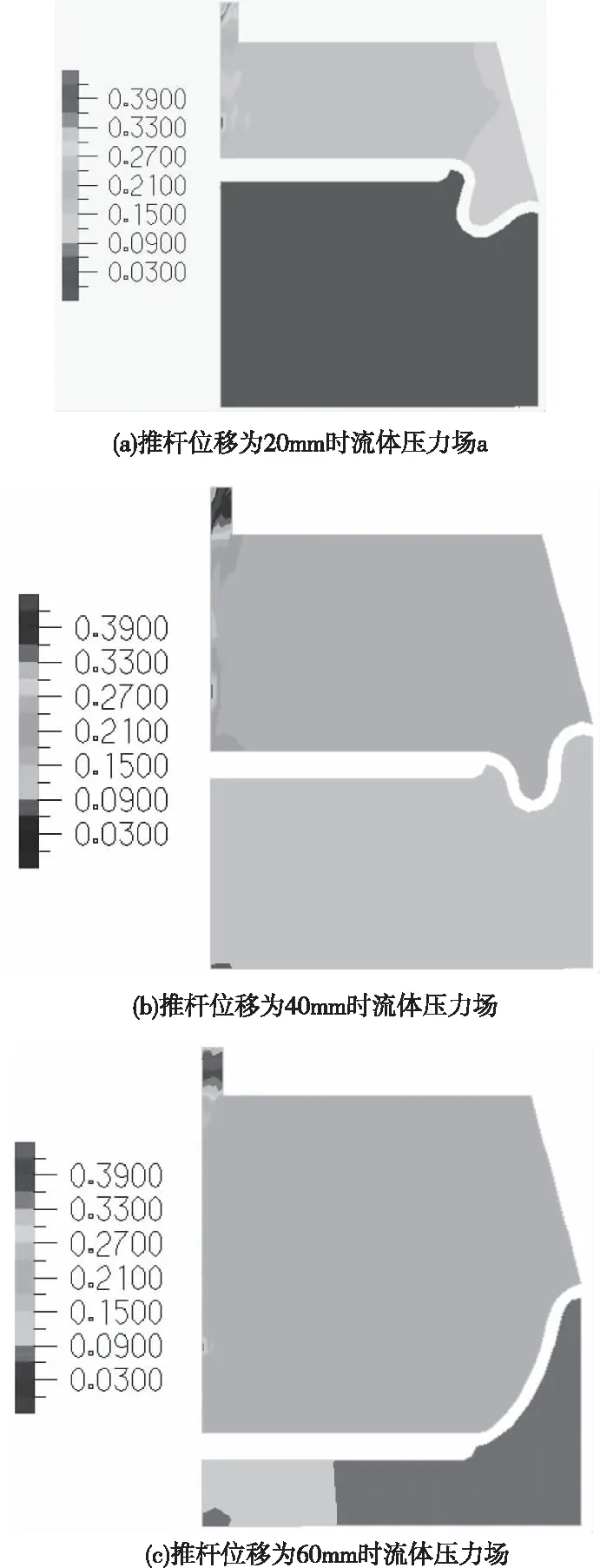
圖10 不同推桿位移情況下流體壓力場

5.3 入口直徑對制動氣室動態響應的影響

圖9和圖10為0.4 Mpa供氣壓力下不同入口直徑時制動氣室壓力響應曲線及推桿位移曲線。由圖可知，入口直徑對制動氣室壓力響應的影響較大，入口直徑越大，制動氣室的壓力響應時間越短。入口直徑為12 mm時，制動氣室的壓力響應時間最短。入口直徑為8 mm時，制動氣室的壓力響應時間最長。然而隨著入口直徑的增大，入口直徑的變大對壓力響應的影響越不明顯。

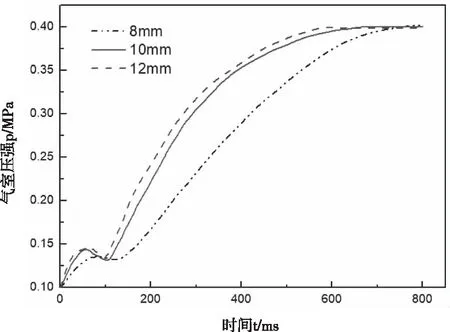
圖11 不同入口直徑下制動氣室壓強曲線

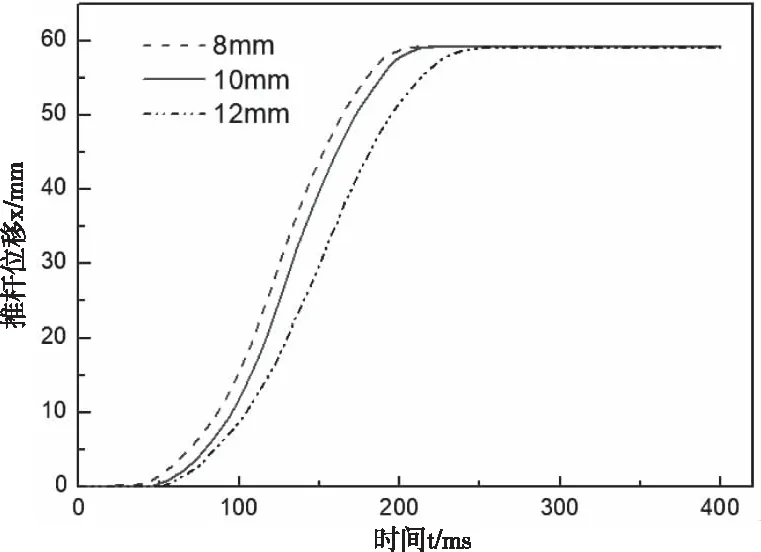
圖12 不同入口直徑下制動氣室推桿位移曲線

6 結論

1)本文建立了膜片制動氣室的流固耦合有限元模型，計算分析其動態特性，并與試驗結果進行對比分析，驗證本文建模方法和計算方法的正確性。

2)分析了入口直徑對制動氣室壓力響應的影響。結果表明，提高入口直徑可以有效增加制動氣室的壓力響應，但入口直徑越大，提高效果越不明顯。

3)本文在諸多假設與簡化條件的基礎上展開建模，在往后的研究中應進一步完善制動氣室的計算模型，更加精準地預測制動氣室地動態特性。