加權K-prototype-粗糙集的航班延誤等級劃分研究

王興隆，紀君柔，石宗北

(中國民航大學空中交通管理學院，天津 300300)

1 引言

隨著航班流的增多，空域資源的緊缺，航班延誤也日益增多，而對航班延誤程度進行有效評估，制定切實可行的航班延誤等級劃分規則是減少延誤成本，進行協同流量管理并且建立相應的應急預案的關鍵依據，具有很大的實際應用價值。

2012年，Raj Bandyopadhyay[1]等使用線性回歸來確定影響航班延誤的因素，并采用分類器(SVM)來分析航班延誤，2017年，Suvojit Manna[2]等采用航班延誤的六個延誤屬性，建立梯度增強決策樹模型用來分析航班延誤。2014年，顧紹康[3]根據時空和空間兩個角度的評估指標建立了航班延誤程度實時評估指標體系，2015年，孟會芳[4]以國內某大型樞紐機場為應用背景，構建了基于投票聚類的一段時間內的航班延誤等級劃分策略，2018年，吳仁彪[5]等人提出了基于雙通道卷積神經網絡(DCNN)的航班延誤預測模型，將延誤時間進行等級劃分，將預測問題轉化為分類問題。

以上研究只是提出數值屬性指標對航班延誤程度進行了評估，同時并未確定具體的判斷準則，本文同時提出數值屬性指標和類別屬性指標，利用加權k-prototypes聚類算法對航班延誤程度進行了等級評估，并進一步結合粗糙集理論知識，利用Rosetta軟件建立了科學有效的延誤航班等級劃分規則，確定了直觀并具有高準確率的延誤等級判斷準則。

2 加權K-prototypes-粗糙集航班延誤等級劃分模型

2.1 航班延誤等級劃分指標選擇

圖1為延誤航班等級劃分流程圖。

圖1 延誤航班等級劃分流程圖

由圖1可知對航班延誤程度的等級進行劃分，需考慮多個能反映航班延誤程度的指標，每個指標均能從某一方面反映延誤狀況，結合我國航空運輸的特點和實際情況，本文提出了6個衡量延誤程度的指標：

1)延誤時間指標

當延誤時間越長，航班延誤成本越高，并對后續航班造成的影響更大，波及延誤更廣，對機場，航空公司以及旅客產生直接的延誤經濟損失，為此選取延誤時間為衡量延誤程度的權重最大的指標。

2)飛行時間指標

飛行時間越長，油耗成本越高，若延誤航班的飛行時間越長，那么在飛行中產生影響航班安全飛行和實際飛行時長的因素幾率就越大，且可能會導致航班需要過夜，增加了航空公司的延誤成本。飛行時間從航空公司角度反映了延誤程度。

3)延誤人數指標

延誤人數越多，產生的旅客經濟損失就越大，這種經濟損失可描述為延誤時間占用了旅客正常的工作時間，延誤人數是從旅客角度評價延誤程度。

4)飛行距離指標

延誤航班飛行距離越長，那么航班經過的管制扇區就相對越多，需要進行管制移交的次數就越多，受影響的管制員就越多，飛行距離是從管制員角度考慮延誤程度。

5)經停指標

延誤航班是否需要經停反映了受影響的機場個數，經停延誤航班不僅對目的地機場產生影響同時也會影響經停機場，航班是否經停是從機場角度確定延誤程度。

6)機型指標

延誤航班機型越大，所需尾流間隔也越大，恢復航班運行難度也相對較大，地面等待以及空中等待經濟損失也越大，機型指標是從等待經濟損失角度確定延誤程度。

6個航班延誤評價指標具體表示如表1所示：

表1 航班延誤等級評價指標

2.2 基于加權K-prototype的航班延誤等級劃分

聚類分析是一種無監督的學習，對應用于大規模數據集的劃分具有很大的優勢，一般的聚類方法如：K-means算法[6]，K-modes算法[7]，RW-CLOPE算法[8]等只能對單一屬性指標數據進行處理，而本文在對延誤航班進行等級劃分時采用的六個評價指標包含了數值屬性指標和類別屬性指標，k-prototype算法[9]是能夠對混合屬性數據進行聚類的一種有效算法。

1)最佳聚類數K的確定

在聚類分析時，最佳聚類數的選擇具有隨機性導致聚類結果穩定性較差，因此本文通過手肘法和輪廓系數法相結合對評價指標進行計算分析確定最佳聚類數，從而保證聚類結果穩定可靠。

手肘法是一種基于誤差平方和(SSE)的K值選擇算法，隨著聚類數K的增大，每個類的聚合程度會逐漸提高，誤差平方和SSE自然會逐漸變小。當K小于真實聚類數時，由于K的增大會大幅增加每個類的聚合程度，故SSE的下降幅度會很大，而當K到達真實聚類數時，SSE的下降幅度會驟減，然后隨著K值的繼續增大而趨于平緩， SSE的計算公式如下

(1)

輪廓系數法的核心指標是輪廓系數(Silhouette Coefficient)，某個延誤航班Xi輪廓系數定義如下

(2)

式中：a是Xi與同類中其它延誤航班的平均距離，b是Xi與最近類中所有延誤航班的平均距離。最近簇的定義為

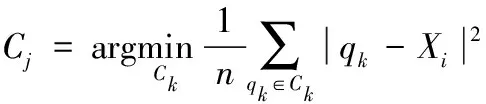
(3)

式中：qk是某個類Ck中的一個延誤航班。

求出所有延誤航班的輪廓系數后再求平均值就得到了平均輪廓系數，平均輪廓系數越大，聚類效果越好。

2) k-prototypes算法的加權改進

在實際航班運行中，不同評價指標在對延誤航班的等級劃分中所占比重也不相同，因此本文對k-prototypes算法進行了加權改進。

設X=[X1，X2，X3，…Xn]為n個延誤航班集合，其中Xi=[xi1，xi2，…xip，…xim]表示具有m個延誤評價指標的第i個延誤航班，1至p下標為數值屬性指標，p+1至m下標為類別屬性指標，Y=[Y1，Y2，Y3，…Yk]為K個類的中心原型延誤航班的集合，其中Yj=[yk1，yk2，…ykp，…ykm]表示第j個類中具有m個評價指標值的中心原型航班。

數值屬性指標之間采用歐幾里得距離計算，計算公式為

(4)

式中：ai1，ai2，…aip為不同數值評價指標的權重值。

類別屬性指標之間的采用海明威距離計算，計算公式為

(5)

相異度距離為

d=d2+γd2

(6)

式中，γ為分類屬性權重值。

采用加權K-prototype聚類算法僅能對每個延誤航班的延誤等級進行劃分，而不能建立有效航班延誤等級劃分規則。

2.3 基于粗糙集的航班延誤等級規則建立方法

本文采取粗糙集理論[10-11]對航班延誤等級進行規則建立，粗糙集理論可以在信息不完整和信息不一致下，用來規約數據集合，發掘隱藏數據相關性，以產生有用的分類規則。

航班延誤等級判別的知識表達系統為S=(U，A，V，f)，其中U為航班延誤特征論域；A為航班延誤屬性集合，由條件屬性C和決策屬性D組成，C={延誤時間，延誤人數，延誤航班機型，飛行距離，是否經停，飛行時間}，D={延誤等級}；V為屬性對應的值域，f：U×A→V是一個航班延誤等級信息函數，為每個航班延誤等級對象屬性賦予一個信息值。航班延誤等級規則生成步驟如下：

1)航班延誤屬性數值進行離散化處理

2)利用Johnson算法進行屬性約簡，屬性約簡的目的是將多余的屬性值刪除

3)等價類和上下近似集的獲取

4)生成航班延誤等級的劃分規則

2.4 模型計算步驟

模型計算步驟如下：

Step 1：輸入樣本數據，結合“手肘法”和輪廓系數法確定樣本數據最佳聚類數K，每個類選取一個中心原型。

Step 2：根據式(6)將樣本分配到距離中心原型最近的那個類，每次分配后，更新類的中心原型。

Step 3：在所有的樣本都分到各自的類中后，重新計算樣本到中心原型的距離。如果一個樣本距離新的中心原型比距原來的中心原型要近，那就重新分配到新的中心原型的類中。

Step 4：重復Step 3，直到沒有樣本對應的類再改變，聚類結束，得到每個航班對應的延誤等級。

Step 5：選取航班延誤特征和對應的延誤等級，基于粗糙集理論構建航班延誤等級識別知識表達體系。

Step 6：采用基于布爾邏輯離散化算法對延誤屬性數據的離散化。

Step 7：采用Johnson貪婪算法，對離散化的航班延誤屬性進行約簡，刪除冗余屬性，提取航班延誤等級劃分規則。

Step 8：計算航班延誤等級規則劃分精度。

3 實例驗證

3.1 數據準備

選取某大型樞紐機場一月份的航班延誤數據，共選取了4557條延誤航班數據作為樣本，因為數據值差異性過大，為了增加結果的準確性，將數值指標根據式(7)進行歸一化處理，將各數值指標取值控制在[0，1]之間。

(7)

其中x為樣本數據，xmin為所有樣本數據的最小值，xmax為所有樣本數據的最大值。經過歸一化后部分樣本數據如表2所示。

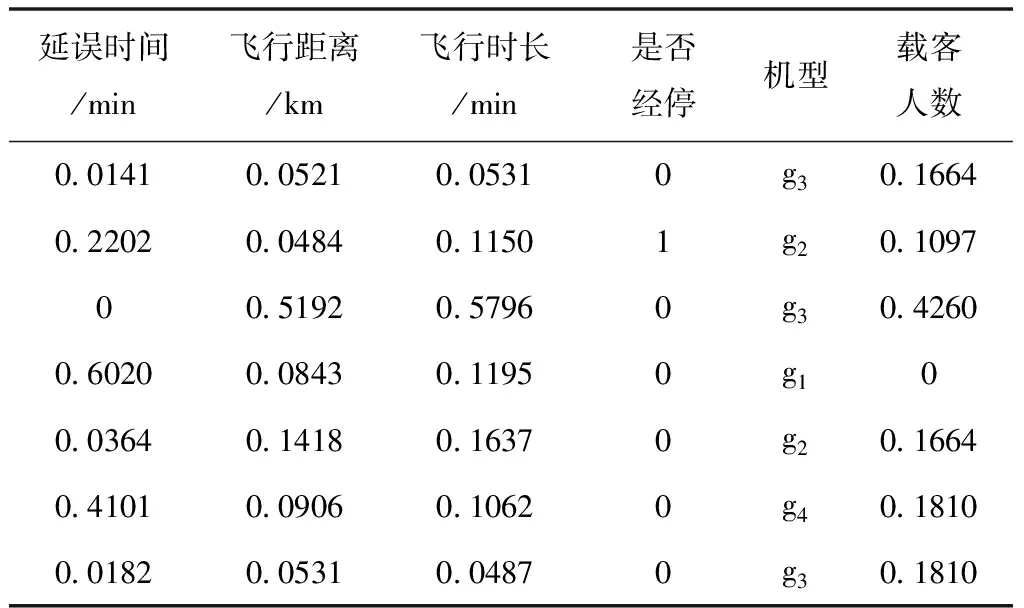
表2 歸一化后的航班延誤數據

3.2 最佳聚類數K的確定

由圖2可以看出該類方法得到的最佳聚類的K的取值可能為3，4，5。

“手肘法”Python實現結果如圖3所示。

由圖3可以看出該類方法K=2時平均輪廓系數最大。

輪廓系數法Python實現結果如圖4所示。

手肘法具體應用于具體的數據集時，會出現如圖2一樣不明顯的“肘點”，導致K值取值具有較大誤差，因此本文同時結合輪廓系數法從而準確的確定最佳聚類數，由圖3可得，在K=2的時候平均輪廓系數最大，因為在K=2時由圖2可看出SSE過大，所以該聚類數不太理想，在K=4的時候，平均輪廓系數也較大，且也符合手肘法得到的K值范圍，綜上所述，本文的最佳聚類數選取為4類。

圖2 “手肘法”折線圖

圖3 輪廓系數法折線圖

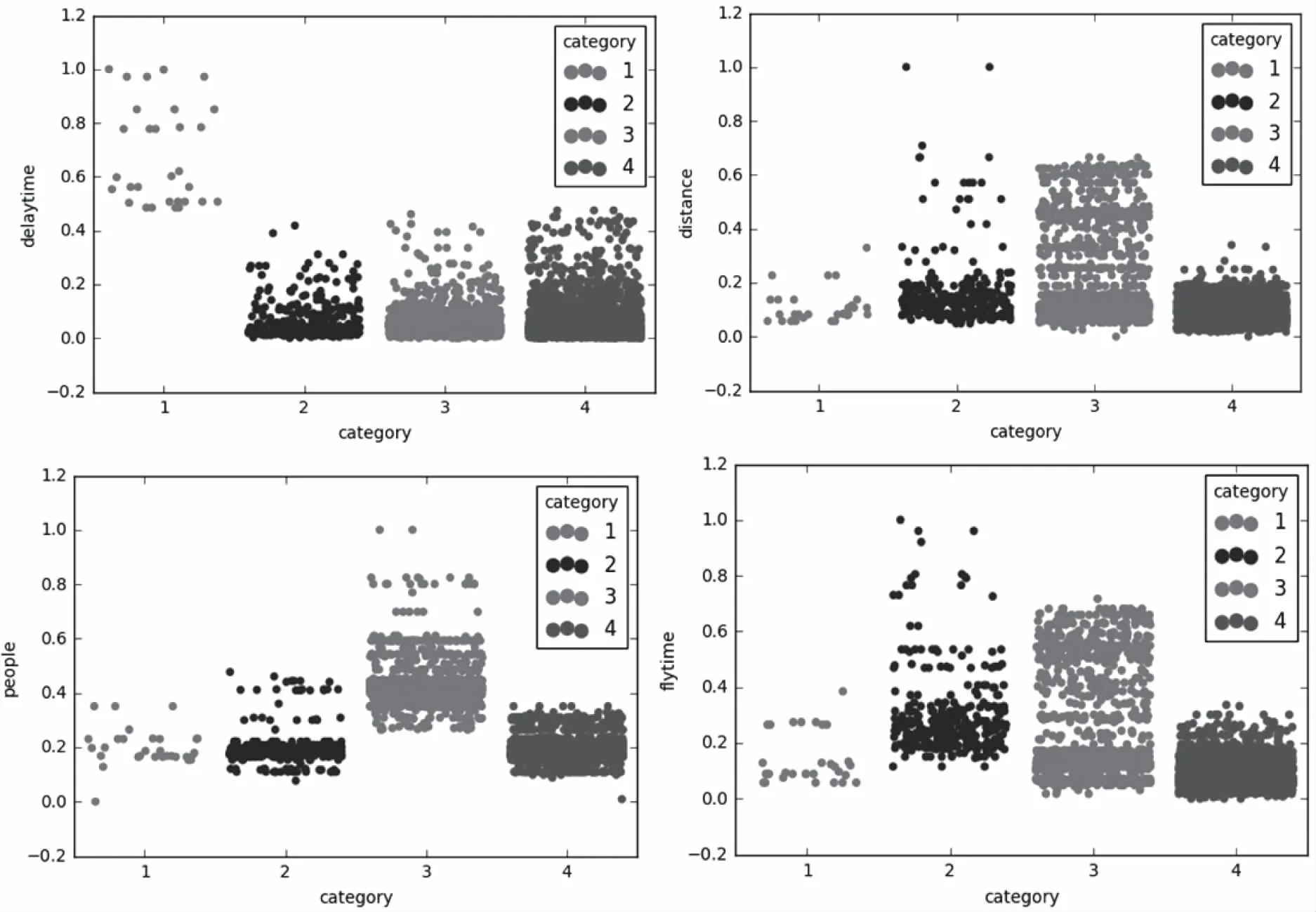
圖4 數值屬性指標分布圖

4 實驗結果分析

本文結合實際航班運行成本將平均延誤時間的權重設置為0.8，飛行距離和飛行時間的權重設置為0.1，載客人數的權重設置為0.4，γ設置為0.2。

當K=4時采用改進的加權K-Prototypes聚類算法得到聚類結果，第一類航班有35架次占比1%，第二類延誤航班有323架次占比7%，第三類延誤航班有1415架次占比31%，第四類延誤航班有2784架次占比61%。

整理每個類別里延誤航班的每個評價指標分布，并進行對比分析，確定每種類別對應的航班延誤級別。延誤等級共有4級，各類延誤指標分布圖如圖4和圖5所示。

由圖4圖5可知，第一類延誤航班的延誤時間遠遠高于其它三類，定義為重度延誤；第三類延誤航班載客人數以及大機型以及超大機型的占比也顯著多于其它兩類，但延誤時間相差不大，定義為中度延誤；第二類延誤航班的六個評價指標均高于第四類延誤航班，定義為一般延誤，則第四類延誤航班定義為輕度延誤。

采用Rosetta 粗糙集軟件利用K-prototype聚類分析的結果作為分析樣本進行計算分析。航班延誤屬性為延誤時間、飛行距離、飛行時間、載客人數、是否經停以及機型，設定決策屬性為輕度延誤、一般延誤、中度延誤、重度延誤。采用Rosetta粗糙集軟件中自帶的 Boolean reasoning(布爾邏輯)算法和 Jonson 貪婪算法進行屬性的離散化和約簡，發現是否經停為冗余屬性，并設置精確度和覆蓋度，得到48條劃分規則，對這些劃分規則結合實際進行整理分析對比得到表3航班延誤等級劃分。

圖5 類別屬性指標分布圖

采用等級判別率GD來衡量該等級劃分規則的精度。指標的計算公式為

(8)

其中，GID為利用等級規則對樣本延誤航班劃分的等級與原先延誤航班樣本等級的差異航班數，N為判斷延誤等級的總樣本航班數。

對樣本延誤航班進行抽樣驗證，得到該等級劃分規則的等級判別率為81.9%，可見該劃分規則精度較高，總體判別結果穩定，能較為準確的劃分航班延誤等級。

表3 航班延誤等級劃分規則表

5 結論

1)本文同時考慮數值屬性和類別屬性評估指標，采用了加權k-prototypes 算法對大量延誤航班聚類分析，為延誤航班劃分了四個延誤等級。

2)利用粗糙集理論結合實際情況，制定了航班延誤等級劃分規則，該規則的等級判別率達到81.9%，提供了直觀有效的航班延誤等級判斷手段。

3)下一步的研究重點就是獲取更多的航班延誤數據，構建更多的反映航班延誤程度的評價指標，建立更為準確的航班延誤等級劃分規則，提高等級判別率，并在對復雜終端區協同調度策略進行研究時考慮航班延誤等級，提高等級劃分模型的實際應用價值。