洪水頻率分析中歷史洪水和古洪水排位方法的統計試驗研究

康 有

(中國電建集團成都勘測設計研究院有限公司，四川 成都 610072)

1 研究背景

科學合理的設計洪水是水利水電工程規劃設計的首要任務，一直是工程水文設計領域的熱點和難點問題之一[1]。目前，國內外設計洪水主要包括數理統計法和成因分析法。數理統計法即為洪水頻率分析途徑，根據實測洪水系列，采用概率論與數理統計的原理和方法，直接計算設計洪水[2]。成因分析法即為水文氣象分析途徑，首先根據實測暴雨系列，計算設計暴雨；然后結合流域產匯流過程，間接計算設計洪水[2]。目前我國設計洪水主要采用洪水頻率分析途徑，直接利用實測洪水系列估計洪水理論總體分布的參數，并據此將頻率曲線外延，推求稀遇頻率的洪水設計值[3]。

通過在實測洪水樣本系列中加入歷史洪水或古洪水資料，進一步擴展洪水考證期，組成不連序洪水樣本系列，進行洪水頻率分析，為確定洪水頻率曲線在稀遇頻率的外延趨勢提供了有力支撐，顯著提高了洪水頻率分析的可靠性和穩定性，這已成為我國水利水電工程設計洪水的寶貴經驗[4]。我國曾廣泛開展了大規模的歷史洪水調查和歷史文獻查閱工作，積累了豐富的歷史洪水資料，其考證期一般在100～200 a，使得洪水考證期得到大幅擴展[5]。現行SL 44—2006《水利水電工程設計洪水計算規范》中針對考慮歷史洪水的非連序洪水系列，采用錢鐵(1964年)提出的經驗頻率修正公式(簡稱“錢穆公式”)計算實測和歷史洪水的經驗頻率[6]。古洪水研究能夠得到比歷史洪水考證期年代更遠的距今數千年的稀遇洪水記錄，其考證期一般在1 000～2 000 a，可使設計洪水從外延變為內插，有效提高了設計洪水的可靠性[7]。實際中常將古洪水資料和歷史洪水資料同等看待，進行洪水分級排位，其經驗頻率采用錢穆公式進行計算。但是，古洪水研究得到的洪水常為極端的、稀遇的非常洪水，其量級顯著大于實測洪水和歷史洪水[8]。在古洪水的考證期內往往會遺漏同等量級的古洪水，其排位存在不可忽略的誤差；且距離首大歷史洪水的時間間隔非常長。在歷史洪水的考證期內遺漏較大的歷史洪水的可能性較小，其排位誤差可以忽略不計；且距離首大實測洪水的時間間隔相對較短。因此，以往將古洪水看作一般量級的歷史洪水，組成一個歷史洪水系列，按照錢穆公式計算經驗頻率，進行洪水頻率分析將可能存在系統性的偏差。

本文采用我國洪水頻率分析推薦使用的P-Ⅲ型分布，采用統計試驗途徑研究古洪水和歷史洪水資料在洪水頻率分析中的排位方法對洪水設計值的影響，以便進一步提高設計洪水成果質量。以長江干流宜昌水文站設計洪水為例，計算其不同排位情況下的洪水設計值，以期為長江流域水利水電工程規劃設計提供更加可靠合理的設計洪水依據。

2 方法原理

2.1 理論分布線型

假定所研究的洪水隨機變量X服從P-Ⅲ型分布，記作X～Г(x;a，α，β)。假設洪水隨機變量X的簡單隨機樣本為(X1，X2，…，Xn)，定義X(m)取(X1，X2，…，Xn)中從大到小排列的第m項數值，令P(Xm)=P(m)，則有從小到大排列的頻率序列P(1)≤P(2)≤…≤P(n)，稱P(m)為頻率次序統計量[9]。我國現行規范中規定：采用頻率次序統計量P(m)的期望值E(P(m))作為適線法的繪點位置，其計算公式為E(P(m))=m/(n+1)。E(P(m))只與樣本容量n和次序m有關，而與采用的概率分布函數形式無關。

2.2 洪水頻率分析

構建基于SCE-UA算法的優化適線法，以P-Ⅲ型分布作為理論總體概率分布，進行參數估計，稱為優化適線法(Curve Fitting Optimization，簡稱“CFO”)。其中，優化變量選取Ex、Cv與Cs/Cv，適線準則采用離差絕對值和準則，求解算法采用精度高且運行效率快的SCE-UA算法。連序洪水系列的繪點位置采用數學期望公式進行計算，非連序洪水系列的繪點位置采用錢穆公式進行計算[10]。

2.3 統計試驗方法

采用一種基于拉丁超立方抽樣的蒙特卡洛統計試驗方法(即Latin Hypercube Sampling & Monte Carlo Statistical Test，簡稱“LM”)，根據給定的洪水頻率總體分布統計參數，進行獨立重復抽樣生成500個服從P-Ⅲ型分布的洪水模擬系列，計算每個系列的統計參數值(Ex、Cv與Cs)和給定頻率P的洪水設計值XP，以檢驗各種方法的優劣[11]。

設定P-Ⅲ型總體分布參數的取值Ex=100，Cv=0.3、0.4、0.5，Cs=2.5、3.0、3.75Cv、4Cv、5Cv，見表1。統計參數值和頻率設計值的無偏性及有效性分別以標準平均絕對誤差(NMAE)和標準均方根誤差(NRMSE)為標準進行定量評價，見表2。各組方案的統計試驗次數Ns取500次，樣本容量n取50，設計頻率P取1%，0.5%，0.2%，0.1%。

表1 統計試驗選用的洪水頻率分布統計參數

表2 參數估計方法優劣評價指標及其含義

在各種統計試驗方案中，將古洪水或歷史洪水作為已知，其量級和考證期均保持不變，分析各統計參數方案下的洪水設計值變化規律，設置6種古洪水和歷史洪水計算方案如下：①基準方案U，不考慮古洪水和歷史洪水。②方案A，古洪水個數取1個，量級取頻率P=1/1 000設計值；歷史洪水個數取1個，量級取頻率P=1/150設計值。③方案B，古洪水個數取1個，量級取頻率P=1/1 000設計值；歷史洪水個數取2個，量級取頻率P=1/150、P=1/120設計值。④方案C，古洪水個數取1個，量級取頻率P=1/1 000設計值；歷史洪水個數取3個，量級取頻率P=1/150、P=1/120、P=1/100設計值。⑤方案D，古洪水個數取3個，量級取P=1/1 000、P=1/900、P=1/800設計值；歷史洪水個數取1個，量級取頻率P=1/150設計值。⑥方案E，古洪水個數取3，量級取頻率P=1/1 000、P=1/900、P=1/800設計值；歷史洪水個數取2個，量級取頻率P=1/150、P=1/120設計值，其考證期N2=150。⑦方案F，古洪水個數取3個，量級取頻率P=1/1 000、P=1/900、P=1/800設計值；歷史洪水個數取3個，量級取頻率P=1/150、P=1/120、P=1/100設計值。

3 統計試驗

3.1 排位方法

古洪水和歷史洪水的洪水分級排位方法一：古洪水考證期內不進行洪水系列排位，各古洪水的重現期等于各自的考證期；歷史洪水考證期內進行洪水系列排位，各歷史洪水的經驗頻率采用數學期望公式計算；實測洪水期內進行洪水系列排位，各實測洪水的經驗頻率采用錢穆公式計算。

古洪水和歷史洪水的洪水分級排位方法二：古洪水考證期內進行洪水系列排位，各古洪水的經驗頻率采用數學期望公式計算；歷史洪水考證期內進行洪水系列排位，各歷史洪水的經驗頻率采用數學期望公式計算；實測洪水期內進行洪水系列排位，各實測洪水的經驗頻率采用錢穆公式計算。

古洪水和歷史洪水的洪水分級排位方法三：古洪水考證期內進行洪水系列排位，各古洪水的經驗頻率采用數學期望公式計算；歷史洪水考證期內進行洪水系列排位，各歷史洪水的經驗頻率采用錢穆公式計算；實測洪水期內進行洪水系列排位，各實測洪水的經驗頻率采用錢穆公式計算。

3.2 試驗結果

(1)參數值統計特性。從參數值的無偏性來講，相對于基本方案U，方案A可以顯著地提高CFO方法的無偏性；隨著古洪水或歷史洪水個數增加，CFO方法的無偏性變劣，見圖1～3。從參數值的有效性來講，相對于基準方案U，方案A可以顯著地提高CFO方法的有效性；但是隨著古洪水或歷史洪水個數的增加，均會降低CFO方法的有效性，見圖1～3。

圖1 CFO方法參數值的無偏性和有效性(方法一)

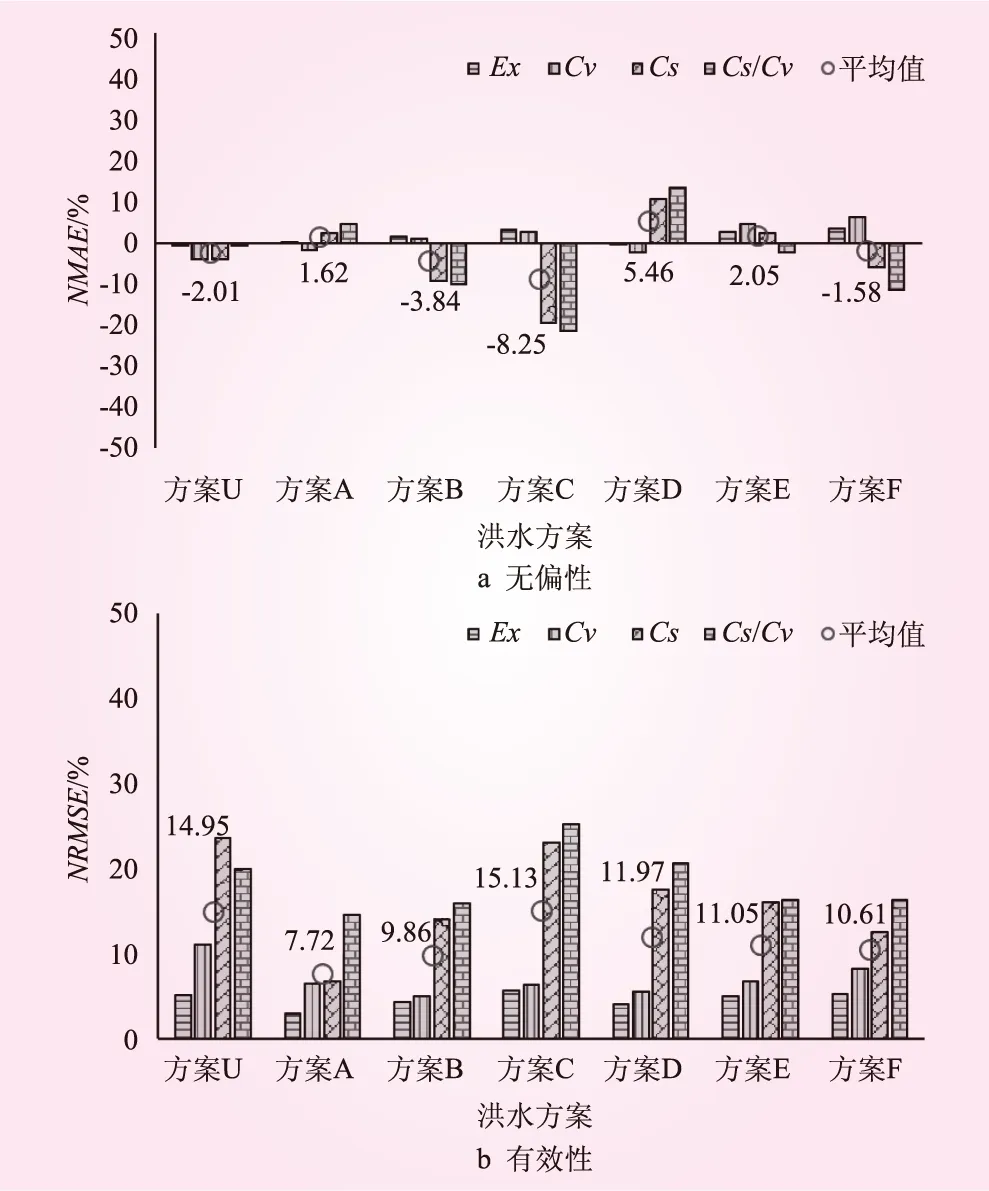
圖2 CFO方法參數值的無偏性和有效性(方法二)

圖3 CFO方法參數值的無偏性和有效性(方法三)

(2)設計值統計特性。從設計值的無偏性來講，相對于基本方案U，方案A可以顯著地提高CFO方法的無偏性；隨著古洪水或歷史洪水個數增加，CFO方法的無偏性變劣；見圖4～6。從設計值的有效性來講，相對于基準方案U，方案A可以顯著地提高CFO方法的有效性；但是隨著古洪水或歷史洪水個數的增加，均會降低CFO方法的有效性；見圖4～6。考慮古洪水或歷史洪水的CFO方法計算的設計值有效性整體上優于沒有考慮古洪水或歷史洪水的CFO方法。

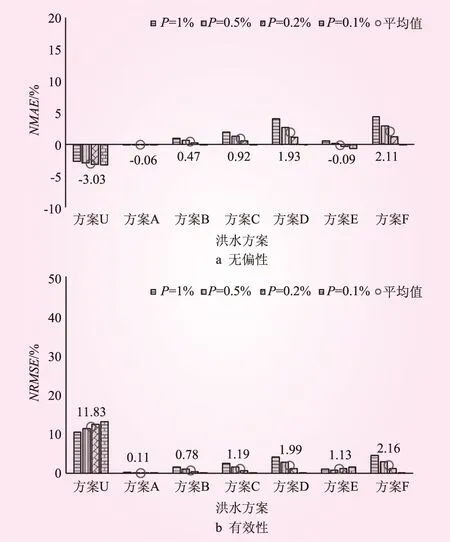
圖4 CFO方法設計值的無偏性和有效性(方法一)

圖5 CFO方法設計值的無偏性和有效性(方法二)

圖6 CFO方法設計值的無偏性和有效性(方法三)

3.3 對比分析

從參數值的無偏性來講，3種排位方法的參數值無偏性指標NMAE分別為-8.06、-0.76、-5.41；參數值有效性指標NRMSE分別為15.89、11.06、13.63，見圖7。由此可見，基于排位方法二的CFO方法在參數值統計特性方面最優。

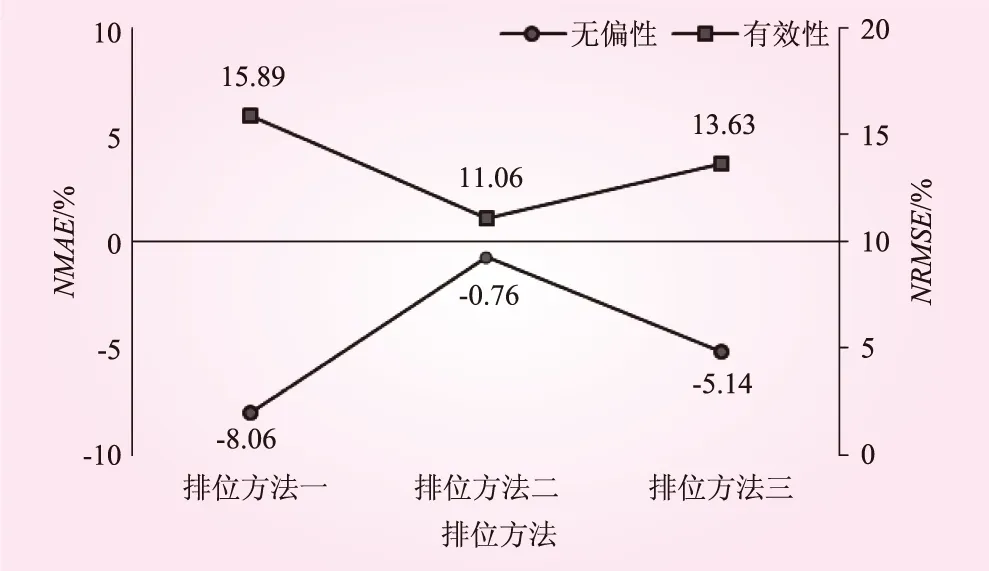
圖7 基于3種排位方法的CFO方法的參數值無偏性和有效性

從設計值的無偏性來講，3種排位方法的設計值無偏性指標NMAE分別為0.88、2.35、3.66；設計值有效性指標NRMSE分別為1.23、2.58、3.72，見圖8。由此可見，基于排位方法一的CFO方法在設計值統計特性方面最優。

圖8 基于3種排位方法的CFO方法的設計值無偏性和有效性

綜上所述，從統計參數值和頻率設計值的無偏性及有效性整體上來講，基于排位方法二的CFO方法統計特性方面整體上最優。另外，古洪水或歷史洪水的個數增加均會使CFO方法統計特性變劣。因此，在實際工作中應根據資料條件開展歷史洪水調查或古洪水研究工作，重點放在確定首大洪水的量級和考證期上，以進一步提高設計洪水成果質量。

4 實例分析

4.1 洪水樣本系列

宜昌水文站位于長江三峽水利樞紐三斗坪壩址下游約43 km，控制流域面積100.55萬km2，占全流域面積的55%，是控制長江上中游來水來沙的咽喉。宜昌站的水文資料觀測始于1877年4月，其資料系列長且翔實，并具有可靠的歷史洪水資料。考慮到三峽水庫于2003年開始蓄水，采用宜昌站1877年～2002年共計126 a年最大洪水系列，8次可定量估計流量的歷史大洪水，以及3次古洪水(包含1870年大洪水)。20世紀90年代，經過古洪水研究后，距今2 500 a以來未發現比1870年更大的洪水，則1870年大洪水的考證期為2 500 a[12]。

4.2 無歷史洪水的洪水頻率分析

根據宜昌站1877年～2002年共計126 a年最大洪水系列，首先采用線性矩法計算統計參數初始值；然后采用基于SCE-UA算法的優化適線法，繪點位置采用數學期望公式計算，優化變量選取Ex、Cv與Cs/Cv，適線準則采用離差絕對值和準則；不考慮歷史洪水和古洪水的宜昌站洪水頻率曲線見圖9。

圖9 宜昌站洪水頻率曲線示意(實測洪水)

4.3 有歷史洪水的洪水頻率分析

將宜昌站126 a實測洪水系列、8個歷史洪水及3個古洪水(包含1870年大洪水)共同組成一個非連序洪水系列，進行年最大洪水頻率分析計算。根據第3節中3種古洪水和歷史洪水的洪水分級排位方法，計算統計參數值及洪水設計值。考慮歷史洪水和古洪水的宜昌站洪水頻率曲線見圖10。

圖10 宜昌站洪水頻率曲線示意 (實測洪水+歷史洪水+古洪水)

4.4 對比分析

對比有無歷史洪水時宜昌水文站的統計參數值(Ex、Cv、Cs)和設計洪水值XP見表3。

由表3可知，基于排位方二的CFO方法計算的頻率P=1%、0.5%、0.2%、0.1%的洪水設計值與不考慮歷史洪水的CFO方法計算的洪水設計值之間相對百分比平均值為15.4%。這說明，加入歷史洪水或古洪水資料后，洪水設計值將會變大。

表3 宜昌站洪水頻率分析計算成果

5 結 論

本文研究了古洪水和歷史洪水資料在洪水頻率分析中排位方法對洪水設計值的影響，并分析評價了古洪水和歷史洪水對設計洪水的作用，為具有古洪水和歷史洪水資料的非連序洪水樣本系列的洪水頻率分析計算提供了試驗依據，其研究結論如下：

(1)考慮古洪水或歷史洪水的CFO方法的統計特性整體上優于不考慮古洪水或歷史洪水的CFO方法，尤其以有效性改善最為顯著；隨著古洪水或歷史洪水個數的增加，均會降低CFO方法的無偏性、提高有效性。

(2)從統計參數值和洪水設計值的無偏性及有效性整體上來講，基于排位方法二的CFO方法統計特性方面整體上最優；也就是，古洪水的經驗頻率采用數學期望公式計算，歷史洪水的經驗頻率采用數學期望公式計算，實測洪水的經驗頻率采用錢穆公式計算。

(3)在實際工作中應根據資料條件開展歷史洪水調查或古洪水研究工作，重點放在確定首大洪水的量級和考證期上，以進一步提高設計洪水成果質量。