基于奇異譜分析的大壩安全監測數據異常值識別技術研究

楊 鴿，范振東，傅春江，劉 陽

(1.杭州國家水電站大壩安全和應急工程技術中心有限公司，浙江 杭州 311122；

2.中國電建華東勘測設計研究院有限公司，浙江 杭州 311122；

3.中國電力技術裝備有限公司，北京 100052)

0 引 言

近年來互聯網、物聯網、大數據等技術的快速發展使實現大壩安全實時診斷成為可能。目前應用較為成功的大壩安全診斷信息系統[1-4]都是對大壩安全監測數據進行分析、實時識別異常數據，據此識別大壩異常運行狀況。因此，及時有效地識別異常監測數據是大壩安全實時診斷的基礎。

目前，在大壩監控領域可見的異常值識別方法按照其原理可以被分為基于包絡域的識別法、基于條件相似性的識別法以及基于數學模型的識別法3類。其中，基于統計回歸數學模型的異常值識別方法通常能夠達到較高的敏感度，同時也不容易將正常值誤判為異常，因此應用最為廣泛。但是，回歸模型的建立通常需要有豐富數據分析經驗的人操作完成。當對監測點極多的高壩或群壩進行監控時，人力成本巨大；同時，不同的操作人員可能出現標準不一致、甚至不準確的情況。此外，統計模型中通常還包括水位、溫度等環境量，而在實際工程中經常出現環境量與效應量不同時報送的情況，這時將無法采用統計模型得出效應量預測值，因而也就無法判斷實測值是否異常。

奇異譜分析(Singular Spectrum Analysis，SSA)是一種融合了傳統時間序列分析、多元統計、動力系統以及信號處理等多領域方法的技術。由于無需先驗信息和正弦波假定，且具有時間序列趨勢分析、周期提取、噪聲去除以及預報功能，目前已被廣泛應用于氣候學、氣象學、地球物理以及海洋科學等學科，在機械工程、經濟學、勘測等領域也有所應用[5-9]。基于奇異譜分析的預測過程對人工操作的依賴極低，因而很容易通過計算機語言實現自動化；此外，基于奇異譜分析的預測值是對歷史數據序列規律的反映，并不需要提供環境量即可得出，因而在環境量沒有及時上報時也可進行預測分析。

為此，本文了構建基于奇異譜分析的大壩安全監測異常值識別方法，對該方法對各類型大壩安全監測數據的分析能力進行論證，探討基于奇異譜的異常值識別技術在大壩安全診斷領域的適用性。

1 基于奇異譜分析異常數據識別原理

基于奇異譜分析的異常值識別的基本流程為：采用奇異譜分析法對歷史數據序列進行分析重構后得出預測值，然后，通過檢驗實測值與預測值之間的殘差是否在合理范圍內來判斷測值是否正常。

1.1 奇異譜分析[5，10-11]

對于長度為n的一維時間序列f0,f1,f2,k…,fn-1，為了了解隱含的時間演變結構，把該序列在時間上滯后排列，得到軌跡矩陣X

(1)

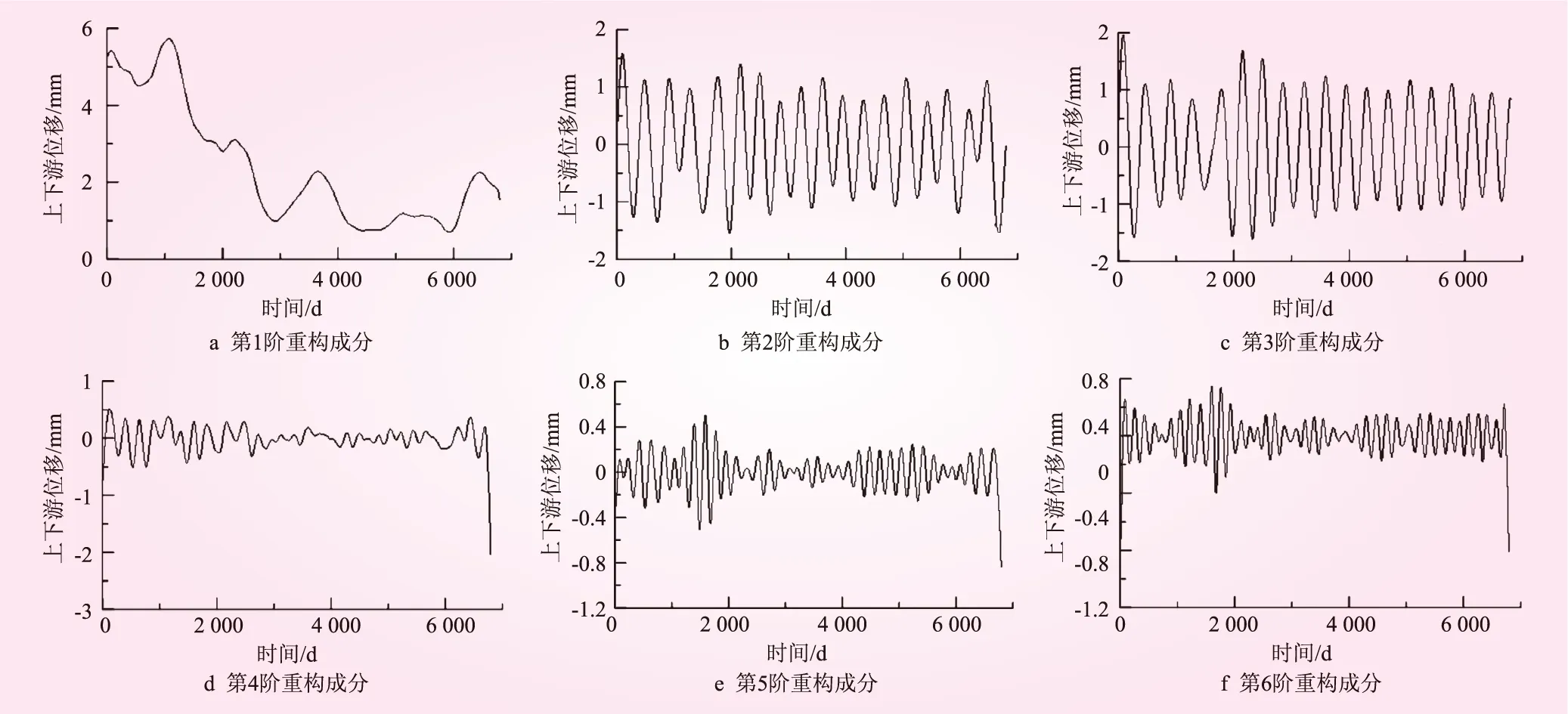
式中，l為窗口長度，且1

然后，對軌跡矩陣進行奇異值分解。令S=XXT，其特征值為λ1,λ2,λ3,…,λl(λ1≥λ2≥λ3,…,λl≥0)，對應的標準正交化的特征向量為U1,U2,U3,…,Ul。令

(2)

其中，d為非零特征值總數。于是，軌跡矩陣的奇異值分解為

X=X1+X2+X3+…+Xd

(3)

(4)

可以證明V1,V2,V3,…,Vl是矩陣ST=XTX的對應于特征值λ1,λ2,λ3,…,λL的標準正交化特征向量；矩陣Xi的秩為1，稱為基本矩陣，或稱第i個重構成分；稱(λi,Ui,Vi)為第i個特征組。

可將d個基本矩陣分為m組，各組分別包括I1,I2,…,Im個基本矩陣。于是，可將軌跡矩陣可以寫作：

X=XI1+XI2+…+XIm

(5)

分組的規則與序列分析的具體目的有關，例如，對序列進行去噪處理時需將特征值較大的基本矩陣分為一組，進行周期成分提取時可將呈現周期特征的基本矩陣分為一組。

最后，對分解或分組后的矩陣進行重構，得到新的數據系列。具體的，對于L×K的矩陣Y，令其元素為yij,L*=min(L,K),K*=max(L,K)，N=L+K-1；若L

(6)

式中，gk為Y中元素的對角平均化，例如，當k=1時，g1=(y12+y21)/2。可以看到，如果Y是某個序列h0,h1,h2,…,hN-1的軌跡矩陣時，得到的序列gk=hk。

(7)

如果式(7)近似成立，則稱X“近似可分”。

1.2 基于奇異譜分析的異常值識別

對于軌跡矩陣X，第k個重構成分的貢獻率CRk為

(8)

表征序列主要特征的成分的貢獻率顯著大于噪聲及粗差的貢獻率。因而，可選用貢獻率顯著較大的主要成分重構數據序列，然后求出重構序列與實測值的殘差，再通過對殘差的分析即可識別異常值。一般可選用累積貢獻率約為85%的的前k個成分重構數據序列。

殘差的判別方法可采用拉依達準則，但為了避免偏離較嚴重的粗差對均值和標準差的估計造成影響，此處建議采用穩健估計粗差探測的IQR準則。具體的，將殘差序列按從小到大排列，求出四分位數Q1，Q2及Q3，對于每個殘差Δi，其IQR準則下的穩健比分數統計量Z為[8-9]

(9)

其中，IQR′=0.741 3×(Q3-Q1)。可以認為當|Z|≥3時為異常值，對應的置信水平為99%。

2 奇異譜分析的適用性研究

奇異譜分析最早是針對寬平穩過程開發[10-11]，而大多數大壩安全監測數據序列都具有較強的趨勢性或周期性，并非簡單的平穩過程。因此，對奇異譜分析在大壩安全監測數據分析中的適用性進行驗證。

具體為分別用指數函數和線性函數與噪聲信號構造數據序列，如圖1所示，然后采用奇異譜分析對其進行分析。取序列長度N=500，時間窗口L=100。由圖1可知，奇異譜分析能夠對非平穩數據序列進行分解和重構。圖2為重構成分的貢獻率，由圖2可知，重構成分的貢獻率隨階次的增加急劇下降，并未出現“多個相近的特征值”的情況。前4階重構成分及其貢獻率如圖3所示，兩個時間序列的第1階重構成分的貢獻率就分別達到了約90%和96%，前4階重構成分的累積貢獻率約達98%和99%；而并未出現需要多個類正弦曲線才能很好重構原序列的情況。

圖1 原始及重構數據序列

圖2 重構成分貢獻率

圖3 主要重構成分

綜上所述，從實際案例分析結果來看，雖然奇異譜分析最早是針對寬平穩過程開發，但這一方法也將適用于非平穩過程，因而也可以被用于大壩監測數據的分析。

3 基于奇異譜分析的大壩異常監測數據識別技術應用

圖4中細線所示為某高拱壩的上下游位移監測成果，采用奇異譜分析對該數據序列進行分解重構和異常值識別，以驗證基于奇異譜分析的異常值識別方法對復雜數據序列的有效。所分析數據序列的N=6 800，頻率為1次/d，序列的變化周期約為1 a，因而取時間滯后窗口L=400。如圖5及圖6所示，前3階重構成分的貢獻率顯著大于之后的成分，且累積貢獻率大于90%。于是選擇前3階成分重構原數據序列，如圖4中粗線所示。實測值與重構序列的殘差頻率分布圖所示，計算殘差序列的四分位數并利用IQR準則進行判別，取|Z|≥3，對應置信度為99%，得到正常測值的取值范圍如圖7中虛線及圖8中灰色陰影所包圍的區域，在上述區域以外的測值即為異常值。

圖4 原監測數據及重構數據序列

圖5 奇異譜分析主要重構成分

圖6 貢獻率

圖7 殘差的頻率分布

圖8 殘差序列及異常值

4 總 結

本文對基于奇異譜分析的大壩安全監測數據異常值識別技術進行了研究，證明了該技術可對趨勢性或周期性數據序列進行分析，驗證了基于奇異譜分析的異常監測數據識別技術在大壩安全診斷領域的適用性和有效性。與基于回歸模型、確定性以及混合模型的異常值識別技術相比，基于奇異譜分析的技術不需要預先人工建立數學模型，在測點數量較多且需要及時反饋的大壩安全智能診斷領域中有較大優勢。此外，由于奇異譜分析不涉及對環境量的考察，因此，可用于環境量缺失情況下的大壩安全監測數據檢驗分析。