破解兩類導數題中的雙參問題
2021-11-10 06:19:48山東省青島市第六十八中學266100王雅朦
中學數學研究(江西) 2021年10期
關鍵詞:解題
山東省青島市第六十八中學 (266100) 王雅朦
在用導數解決關于函數、不等式、方程等問題中,常會出現一類雙參問題,即給出x1,x2滿足的范圍求參數范圍,或者是給出x1,x2的關系式解決其它問題,由于此類問題比較復雜,對數學思維能力要求較高.本文從典型題目的分析求解出發,通過點評揭示問題解決的一般方法及基本思路,供同學們參考.
一、兩個函數中“存在”與“任意”求參數范圍問題
1.兩個都是“任意”條件下不等式成立
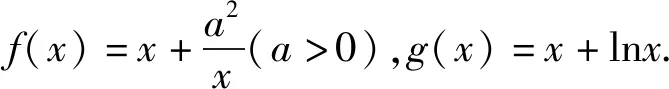
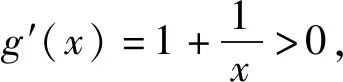
點評:由于題目中的雙參x1,x2都是范圍內的任意,所以不等關系就可以翻譯成兩個函數的最小值與最大值之間的大小關系問題,這個轉化為解題指明了方向.
2.一個“任意”,另一個“存在”條件下的不等式成立
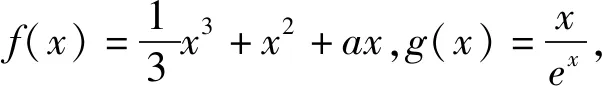
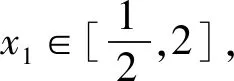
點評:由于題目中的雙參x1,x2所對應的范圍性質與上題不一樣,首先必須確定是求兩個函數的最大值還是最小值問題,實際上是兩個函數最大值之間的比較.
3.使得兩個函數值相等問題
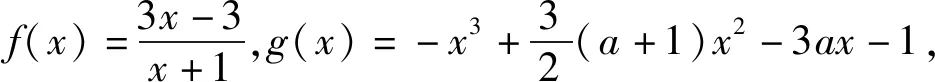
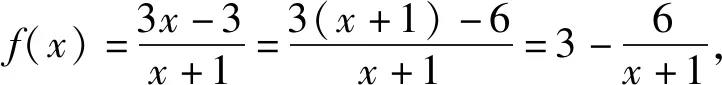
點評:由于題設是總存在兩個函數值相等,即兩個函數的值域含有交集,所以分別求出兩個的值域就成為解決問題的主攻方向.
二、一個函數式的轉化
1.證明不等式
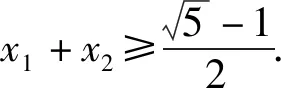
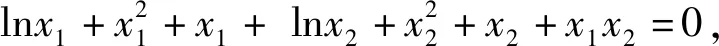
點評:在題目的證明過程中,根據已知條件對所給式子進行配湊,將其轉化為與待證的結論相關的關系式是解題關鍵,它明確了下一步解題的方向.
2.恒成立求參問題
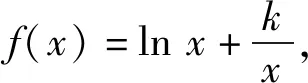
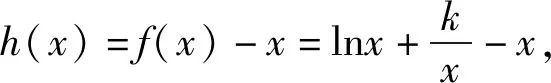
點評:通過對給出的雙參不等式變形后再構造,推出了一個新函數的單調性,再利用此單調性轉化出一個恒不等式,順利解決了參數范圍問題.一覽操作過程,合理流暢.
3.求最大值問題
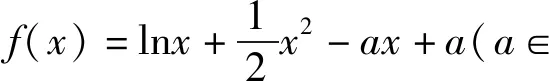
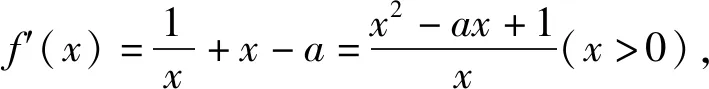
點評:此解法抓住已知條件,對待求最大值的式子進行化簡、配湊,使其轉化為求一個新函數的最大值問題,這里的有目的的轉化是解題的關鍵.
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
數學小靈通·3-4年級(2017年12期)2018-01-23 03:37:54
數理化解題研究(2017年4期)2017-05-04 04:07:56
讀寫算(下)(2016年11期)2016-05-04 03:44:22
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
中學生數理化(高中版.高二數學)(2016年10期)2016-03-01 03:46:37

